Determination of an Indicator Constant: a Study of Bromocresol Green
TOC/Help. Click to here expand/hide
Overview
Background
Pre-lab work
Experimental
Post-lab work
![]() For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
Overview
In this lab you will use a combination of spectrophotometric and pH measurements to determine the acid dissociation constant of the acid/base indicator bromocresol green.
Learning Objectives
- Employ concepts of acid-base chemistry and spectrophotometry to (experimentally measured and mathematically derived) to determine the acid dissociation constant of a colored indicator.
- Explain how speciation of a weak acid, colored indicator in solution is controlled by the pH of the solution.
- Predict the impact of activity on the speciation of a weak acid, colored, indicator in solution.
To cite this lab manual: “Determination of an Indicator Constant: A Study of Bromocresol Green”. A Manual of Experiments for Analytical Chemistry. Department of Chemistry at UW- Madison, Summer 2024.
Visual Abstract
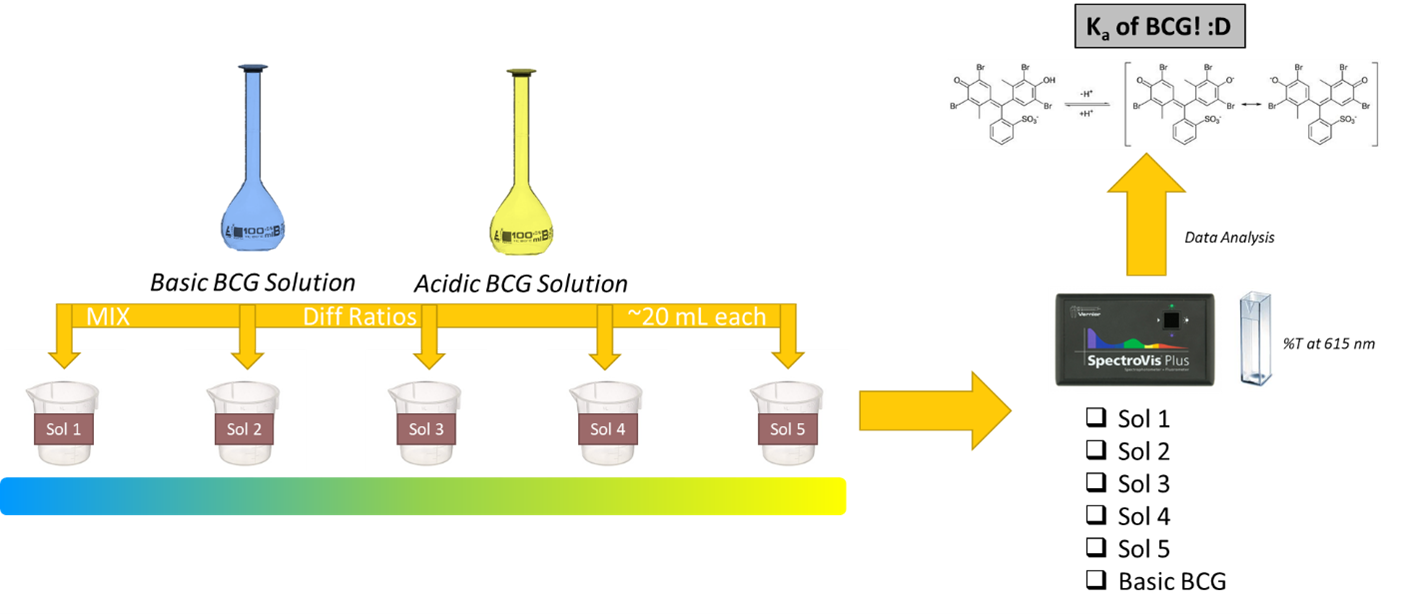

Background
The Acid-Base Equilibrium of an Indicator
An acid/base indicator is a chemical, occurring naturally or derived synthetically, that displays different colors depending on the pH of the solution in which it is dissolved. An acid/base indicator is itself a weak organic acid or base. The protonated (acidic) form differs in color from its deprotonated (basic) form. The equilibrium constant for the conversion of the acidic form of the indicator to the basic form is simply an acid dissociation constant, Ka. Knowing this constant tells us the transition range of the indicator – the pH around which it changes color.
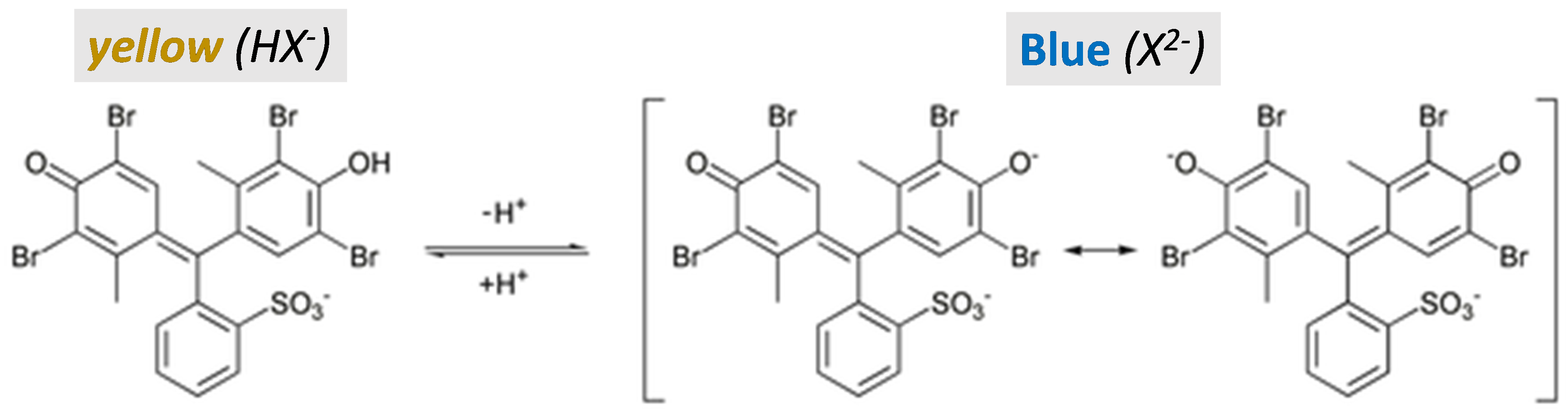
You will study the indicator bromocresol green, which is the indicator that you may have used to standardize an HCl solution. Bromocresol green (3',3'',5',5''-tetrabromo-m-cresolsulfonephthalein) is a sulfonic acid available as the sodium salt shown in Figure 1 on the left (yellow). The fully protonated form of bromocresol green has two acidic hydrogens and, therefore, bromocresol green has two acid dissociation constants (pKa). The first acid dissociation constant involves the proton on the sulfonic acid group, R—SO3H. Sulfonic acids are strong (pKa<1) and the first proton is readily lost, yielding the left structure shown in the figure.
When bromocresol green is used as an indicator, the second acid dissociation involves the characteristic yellow-blue color change. Can you guess which functional group contributes the second proton? If you guessed the alcohol group, you are correct. Although an alcohol group is usually not very acidic, the presence of the benzene ring increases the acidity of this group in bromocresol green. The resulting basic form, a dianionic species, cannot be represented by a single structure. Instead, it can be thought of as a resonance hybrid of the two dominant structures shown in Figure 1 (right, blue).
The second acid dissociation reaction for bromocresol green can be written in abbreviated form as
| HX¯(aq, yellow) ⇄ H+(aq) + X2-(aq, blue) | (1) |
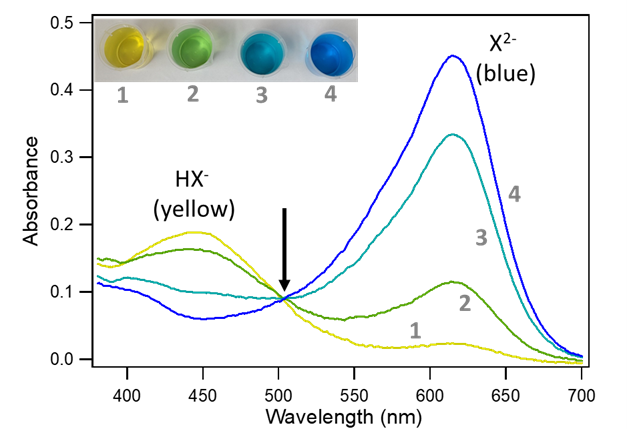
In Equation 1, HX¯ denotes the weak acid form, which appears yellow in solution and is shown in Figure 1 left. X2- denotes the resonance structures in Figure 1 and is blue. Any solution of bromocresol green will contain a mixture of HX¯ and X2-, and the pH of the solution will determine their relative amounts. The absorption spectra for the two forms of bromocresol green are shown in Figure 2. Notice that the color of each species corresponds to the wavelengths that it does not absorb—HX¯ appears yellow because it absorbs light in the blue region of the spectrum, and X2- appears blue because it absorbs light mostly in the red region.
The equilibrium expression for the reaction in Equation 1 is:
| [latex]K_a = \dfrac{\mathcal{A}_{_{H^+}} \mathcal{A}_{_{X^{2-}}}}{\mathcal{A}_{_{HX^-}}} = \dfrac{\mathcal{A}_{_{H^+}} [X^{2-}]}{[HX^-]} \left(\dfrac{ \gamma_{_{X^{2-}}}}{\gamma_{_{HX^-}}}\right)[/latex] | (2) |
The activity coefficients in Equation 2 can be calculated and AH+ measured with a pH meter. If we can determine the concentrations of HX¯ and X2-, then all the quantities on the right-hand side of the equation are known and we can calculate Ka. Since both forms of these species are colored, absorption spectrophotometry allows us to determine their concentrations.
But first, we will derive an expression for the fractional composition of X2-, αX2-, in terms of measured absorbances, and express the ratio [X2-]/[HX¯] in terms of those absorbances. The total (or formal) concentration of bromocresol green in solution, [BCG], is a sum of the concentration of the two species:
| [BCG] = [HX¯] + [X2-] | (3) |
Note that in the equation above, the concentration of the fully protonated form of bromocresol green, H2X, has not been included. This is because it is such a strong acid (pKa<1) that in the pH range we consider, its concentration is negligible. In other words, we have simplified the problem from a diprotic acid system to a monoprotic acid system. Then, the fractional composition of X2- is simply defined as:
| [latex]\alpha_{_{X^{2-}}} = \dfrac{[X^{2-}]}{[BCG]} = \dfrac{[X^{2-}]}{[HX^-] + [X^{2-}]}[/latex] | (4) |
Spectrophotometric Determination of the Concentrations
Now recall that for a mixture of two absorbing species, the absorbance measured at any particular wavelength will be a sum of the absorbances of each species at that wavelength. That is, for bromocresol green,
| Asample = AHX¯ + AX2- | (5) |
where Asample is the total absorbance of the solution measured at a specific wavelength, λ, and AHX¯ and AX2- are the absorbances of the individual species at λ.
One way to determine the concentration of each species in the mixture is to choose a wavelength where one species is strongly absorbing and the other is not. It can be seen from Figure 2 that a wavelength near 615 nanometers meets this criterion. At 615 nm the absorbance of X2- is at a maximum, while that of HX¯ is negligible. The measured absorbance at 615 nm is due entirely to X2-. That is, at 615 nm, Asample = AX2-. From Beer's Law, we can then say that for a sample containing a mixture of HX¯ and X2-:
| [latex][X^{2-}] = \dfrac{A_{sample}}{\left(\epsilon_{X^{2-}}^{615}\right) b}[/latex] | (6) |
where Asample is the absorbance measured at 615 nm, [latex]\epsilon_{X^{2-}}^{615}[/latex] is the molar absorptivity of X2- at 615 nm, and b is the path length of the sample cell.
Now suppose we have a second sample that has the same formal concentration of bromocresol green ([BCG]) as the first sample, but that the pH is basic enough that essentially all the indicator is in the form of X2- (Figure 2, line 4). In a basic solution HX¯ readily loses its proton to form X2-, making the concentration of HX¯ negligible. Beer's Law then gives us:
| [latex][BCG] = [X^{2-}] = \dfrac{A_{basic}}{\left(\epsilon_{X^{2-}}^{615}\right) b}[/latex] | (7) |
where Abasic is measured at 615 nm. Substituting Equations 6 and 7 into Equation 4 yields
| [latex]\alpha_{_{X^{2-}}} = \dfrac{\dfrac{A_{sample}}{\left(\epsilon_{X^{2-}}^{615}\right) b}}{\dfrac{A_{basic}}{\left(\epsilon_{X^{2-}}^{615}\right) b}} = \dfrac{A_{sample}}{A_{basic}}[/latex] | (8) |
The sum of all the fractional compositions of the indicator must equal one. Since there are only two forms of bromocresol green present, αHX¯ = 1 - αX2-. Using Equation 8, we can write the ratio of the two species as:
| [latex]\dfrac{[X^{2-}]}{[HX^-]} = \dfrac{\alpha_{_{X^{2-}}}}{1 - \alpha_{_{X^{2-}}}} = \dfrac{\dfrac{A_{sample}}{A_{basic}}}{1 - \dfrac{A_{sample}}{A_{basic}}} = \dfrac{A_{sample}}{A_{basic} - A_{sample}}[/latex] | (9) |
Finally, if we substitute Equation 9 into Equation 2, we get a useful expression for the equilibrium constant Ka in terms of variables we can either measure or calculate:
| [latex]K_a = \left(\mathcal{A}_{_{H^+}}\right) \dfrac{A_{sample}}{A_{basic} - A_{sample}} \left(\dfrac{ \gamma_{_{X^{2-}}}}{\gamma_{_{HX^-}}}\right)[/latex] | (10) |
In this lab, you will use Equation 10 to determine the Ka for bromocresol green. First you will prepare a series of solutions with the same formal concentration of bromocresol green but differing in pH. Thus, each solution will have different proportions of the two forms of the indicator. You will use an acetic acid buffer to control the pH of the solution in which the indicator is added. You will determine AH+ from (a) measurements of pH and (b) calculations based on the known amounts of buffer components used. Once you measure the absorbance of each solution and calculate the activity coefficients for HX¯ and X2-, you will be able to calculate Ka.

Lab Concept Video
click here to hide the video (for printing purpose).
Write down your observations or notes from the video in your lab notebook.
Pre-lab Work

Lab Skills
Review these lab skills videos prior to lab.
click here to hide the video playlist (for printing purpose).
Key Takeaways
- This experiment requires careful use of glassware to quantitatively calculate the pKa of bromocresol green.
- The spectrophotometer has a few nuances you should be aware of, including orientation of the cuvette, how to set up for measurements (absorbance vs. percent transmittance), and blanking procedures.
Extra Resources:
- How to use a SpectroVis Plus
- How to Calibrate a pH Probe
- Making Scientific Plots
- Finding Property Data

Prelaboratory Exercises
Write out the answers to the following questions in your lab notebook before coming to lab.
- Calculate the ionic strength of a solution containing 0.01 M sodium acetate, 0.09 M potassium chloride, and 1.1 × 10-5 M bromocresol green. (You will prepare this solution in Step 1 of the experimental procedure.)
- Calculate the ionic strength of a solution containing 0.01 M acetic acid, 0.10 M potassium chloride, and 1.1 × 10-5 M bromocresol green. (You will prepare this solution in Step 2 of the experimental procedure.)
- You should have obtained the same result for questions 1 and 2 above. Explain why more potassium chloride is needed in the second solution to achieve the same ionic strength as the first solution.
- There are several models to choose from when calculating a predicted activity of an ion in solution. The most general of these models is the Davies Equation (used in the Adventures with Buffers experiment), which is a good choice for a system where the hydrated radius of a species in unknown or for systems at higher ionic strength as it works for ionic strengths up to 0.5 M. For systems where the hydrated ion radius is well known and for ionic strengths up to 0.1 M, the extended Debye-Hückel equation is an excellent and more accurate choice for predicting the measured activity of components in solution. Use the extended Debye-Hückel equation to calculate the activity coefficients of H+ (γH+) and acetate (γAc¯) in a solution with an ionic strength of μ = 0.1 M. (Consult your textbook for information on the equation and a table of activity coefficients.)
- What is the activity coefficient for acetic acid? Explain.
- The extended Debye- Hückel equation makes use of the parameter α, the hydrated diameter of the ion, to determine activity coefficients. The appropriate value to use for this parameter is not always known, which is true for bromocresol green. For such cases, the Davies equation below can be used:
[latex]-\log \gamma_z = 0.51 z^2 \left( \dfrac{\sqrt{\mu}}{1 + \sqrt{\mu}} - 0.3 \mu \right)[/latex] (11) where z is the charge of the ion. Calculate the activity coefficients for the acidic and basic forms of bromocresol green, γHX¯ and γX2¯, for a solution with an ionic strength of μ = 0.1 M.

Before You Take The Quiz on Canvas
- Finish the prelaboratory questions above.
- Have a clear idea on how to calculate the acid dissociation constant from absorbance measurements using the procedure described below. (You could complete the theoretical portion of the answer sheet before taking the quiz.)

Experimental
- Prepare a basic solution of bromocresol green by adding 10.0 mL of 0.100 M sodium acetate, 10.0 mL of stock bromocresol green solution, and 9.0 mL of 1.0 M potassium chloride to a 100 mL volumetric flask. Dilute to the line with distilled water and mix thoroughly. The concentration of the bromocresol green in this solution is about 1.1 × 10-5 M.
- Prepare an acidic solution of bromocresol green by adding 10.0 mL of stock 0.100 M acetic acid solution, 10.0 mL of the stock bromocresol green solution, and 10.0 mL of the 1.0 M potassium chloride solution into a 100 mL volumetric flask. Dilute to the line with distilled water and mix thoroughly.
Think about how the procedure leverages potassium chloride to set the ionic strength constant for both the acidic and basic solutions you’ve created.
- Prepare a series of five buffered bromocresol green solutions by mixing V mL of the basic solution with (20 – V) mL of the acidic solution in small beakers. The total volume of each solution should be 20 mL. For instance, one solution could have 5.00 mL of basic solution mixed with 15.00 mL of acidic solution. A range of 5 mL to 15 mL for V will give optimum results; the details of these choices and how to make the solutions are up to you and your lab partner.
- Measure the pH of each of the buffered solutions by inserting the measuring electrode of the pH meter directly into each of the five beakers. Be sure to rinse and dry off the electrode before inserting them into the next solution.
- Measure the percent transmittance of each solution at 615 nm using the spectrophotometer following the procedure for making transmittance measurements using the lab spectrometers.
Post-Lab Work Up

Results/Calculations
Fill out the answer sheet for this experiment completely. Answer the following post-lab questions.
- Using your measured pH values to determine the measured hydrogen ion activity, AH+, for each of the buffered bromocresol green solutions. Keep in mind that pH = – log (AH+).
- The bromocresol green solutions were buffered with a series of buffer solutions by mixing different volumes of acidic (containing acetic acid) and basic (containing acetate) bromocresol green solutions. Using the concentrations and volumes of these solutions, calculate what you would expect the H+ ion activity and pH to be for each solution. What is the difference between your measured and calculated pH value for each solution? (Hints: You can use the Henderson-Hasselbach equation. Keep in mind that the conjugate acid/base pair is acetic acid/acetate and that the Ka for acetic acid 1.75 × 10-5. Include activity coefficients from the extended model in your calculations.)
- Use Equation 9 to calculate the ratio of [X2-]/[HX¯] for each solution.
- Use your results and Equation 10 to calculate values for the Ka and pKa of bromocresol green. Compute the average and standard deviation of pKa.
- Equation 2 can be rearranged to yield the Henderson-Hasselbach equation:
[latex]pH = pK_a + \log \dfrac{[X^{2-}] \gamma_{_{X^{2-}}}}{[HX^-] \gamma_{_{HX^-}}}[/latex] (12) (You should be able to derive this equation.) The activities used in this determination should be calculated using the Davies equation. A plot of pH as a function of the log term should yield a straight line with a slope of 1 and a y-intercept of pKa. Construct such a plot of your data in Excel using the measured pH values. Do a least-square linear fit and determine pKa.

Challenge Questions
Challenge questions are designed to make you think deeper about the concepts you learned in this lab. There may be multiple answers to these questions! Any honest effort at answering the questions will be rewarded.
- Describe the role potassium chloride plays in the chemistry of the equilibrium explored in this lab. How would the omission of KCl from the procedure impact the experimentally determined pKa of bromocresol green?
- Remember, the selection of 615 nm in this experiment was on purpose: the contribution of HX¯ to the absorbance was negligible compared to X2-, and we could simplify our math to calculate Ka. Some spectrophotometers are confined to a smaller range of wavelengths and 615 nm may be outside the scan range of the instrument. Thus, instead of using the peak absorbance of X2-, what if we used the peak absorbance of HX¯ to derive an equation for Ka? Starting with Equation 5, re-derive Equation 10 at 450 nm. Remember that Asample is NOT equal to AX2- anymore.

Lab Report Submission Details
Submit your lab report on Canvas as 1 combined PDF file. This submission should include:
- The completed answer sheet.
- Your lab notebook pages associated with this lab, which should include answers to the post-lab questions and challenge questions.
The grading rubric can be found on Canvas.
References:
- Harris, D. C. & Lucy, C. A. Quantitative Chemical Analysis, 10th ed.; W. H. Freeman: New York, NY, 2020
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please ask your instructor or TA.)
