Adventures with Buffer Solutions
TOC/Help. Click to here expand/hide
Overview
Background
Pre-lab work
Experimental
Post-lab work
![]() For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
Overview
In this experiment you will prepare a buffer solution, study the pH changes of a buffer upon dilution or addition of acid/base, and determine the buffer capacity.
Learning Objectives
- Apply concepts of acid-base chemistry to design a buffer with target pH and capacity.
- Use activity corrections to align a predicted pH with a measured, experimental value.
To cite this lab manual: “Adventure with Buffer Solutions”. A Manual of Experiments for Analytical Chemistry. Department of Chemistry at UW- Madison, Spring 2025.
Visual Abstract
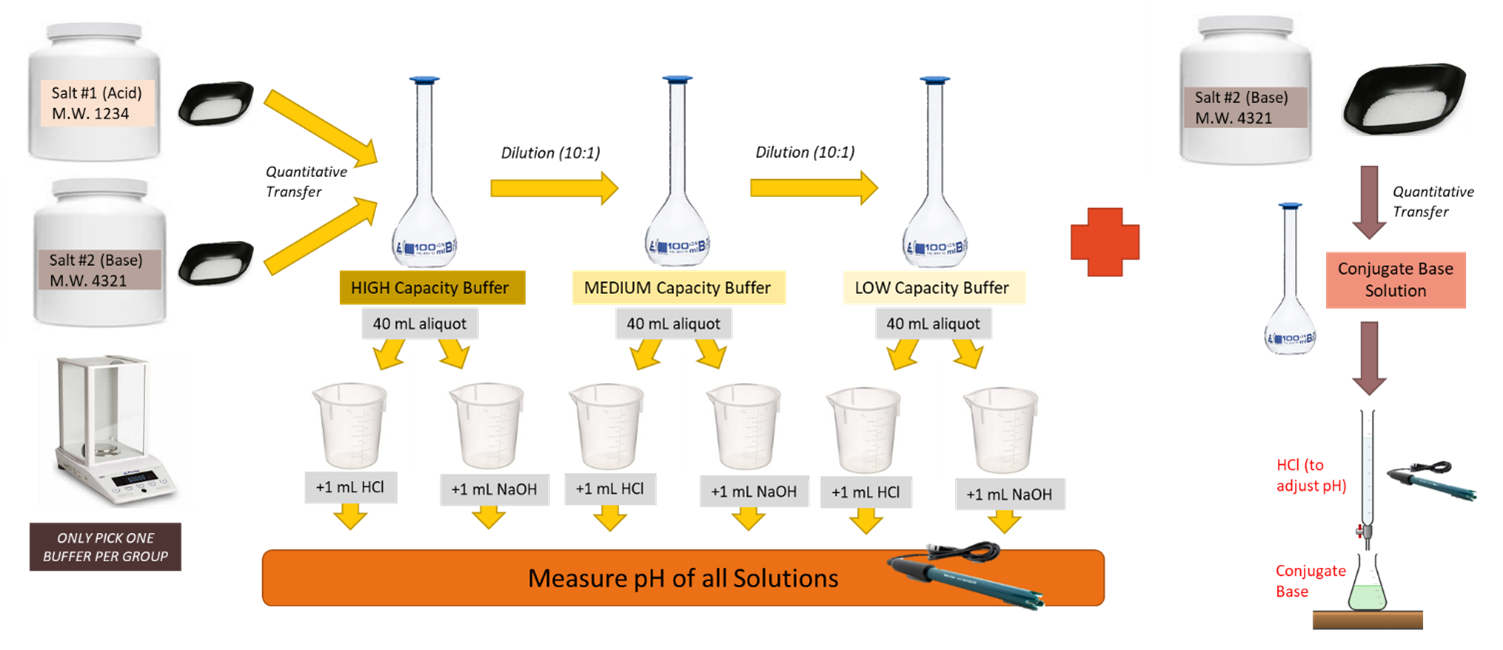

Background
A buffer solution can resist a change of pH when either an acid or a base is added, or if it is diluted. Buffer solutions play important roles in biological and environmental systems. For example, buffers set the pH of blood, saliva, stomach acid, and contents of our digestive tracks. The pH of blood, for example, is primarily regulated by the carbonic acid CO2(g)—H2CO3(ℓ)—HCO3¯(ℓ) buffer system, which maintains a constant blood pH of 7.40.1 Buffers in the lakes and oceans help to maintain healthy oxygen and soluble mineral levels for plants, animals and organisms that live there. Buffers in lakes, streams, and oceans also help to neutralize acid rain falls.
Buffer solutions are typically made of a mixture of weak acid (HA) and its conjugate base (A¯). To understand why such conjugate acid/base mixtures can resist pH change, we first discuss how to calculate the pH of buffer systems. This is done using the Henderson-Hasselbalch (H-H) equation:
| [latex]pH = pK_a + \log \dfrac{[A^-]}{[HA]} [/latex] | (1) |
where [A¯] is the concentration of the conjugate base of the buffering species, [HA] is the concentration of the conjugate acid form, Ka is the acid dissociation constant of the acid, and p is the mathematical operation of -1·log (argument).
Consider the specific carbonic acid system described above as an example:
| HCO3H + H2O ⇄ HCO3¯ + H3O+ | Ka1 = 4.46 × 10-7 | (2) |
| pKa1 = -log (4.46 × 10-7) = 6.35 |
When the ratio of the concentrations of carbonic acid [HCO3H] and hydrogen carbonate [HCO3-] are equal, the log term becomes 0, and the pH is simply pKa1 of the carbonic acid system. As the ratio of [A-]/[HA] changes in a buffer, the pH will change accordingly. Now we can see how buffers resist pH changes:
- When the buffer solution is diluted, the concentration of both A- and HA will be diluted, but the ratio [A-]/[HA] is maintained, meaning the pH does not change. (There is a limit to such dilution before this simple H-H equation calculation breaks down, though.)
- When acid or base is added to the buffer solution, they first need to react with the conjugate base or acid in the mixture to convert them into its respective conjugate form. Now, following the H-H equation (1), a change of the [A-]/[HA] of 10 will only lead to a pH change of 1. This contrasts with the large pH change measured when a strong acid or strong base is simply added to pure water. Now we can also appreciate that for a mixture of weak acid and its conjugate base to act as an effective buffer, both species must be present in appreciable concentrations, to consume appreciable amounts of added acid or base.
Many acids (or bases) can give out (or accept) multiple protons when they dissociate, as simply represented below for a generic triprotic acid (H3A):
| [latex]H_3 A \;\xrightleftharpoons[]{K_{a_1}}\; H_2 A^- + H^+ \;\xrightleftharpoons[]{K_{a_2}}\; HA^{2-} + H^+ \;\xrightleftharpoons[]{K_{a_3}}\; A^{3-} + H^+[/latex] | (3) |
We can calculate the fractional composition (α fraction) for any species from a triprotic acid H3A as a function of pH using the following set of equations:
| [latex]\alpha_{H_3A} = \dfrac{[H^+]^3}{[H^+]^3 + [H^+]^2 K_{a_1} + [H^+] K_{a_1} K_{a_2} + K_{a_1} K_{a_2} K_{a_3}}[/latex] | (4) |
| [latex]\alpha_{H_2A^-} = \dfrac{[H^+]^2 K_{a_1}}{[H^+]^3 + [H^+]^2 K_{a_1} + [H^+] K_{a_1} K_{a_2} + K_{a_1} K_{a_2} K_{a_3}}[/latex] | (5) |
| [latex]\alpha_{HA^{2-}} = \dfrac{[H^+] K_{a_1} K_{a_2}}{[H^+]^3 + [H^+]^2 K_{a_1} + [H^+] K_{a_1} K_{a_2} + K_{a_1} K_{a_2} K_{a_3}}[/latex] | (6) |
| [latex]\alpha_{A^{3-}} = \dfrac{K_{a_1} K_{a_2} K_{a_3}}{[H^+]^3 + [H^+]^2 K_{a_1} + [H^+] K_{a_1} K_{a_2} + K_{a_1} K_{a_2} K_{a_3}}[/latex] | (7) |
These equations can be graphed together into an α-plot to show the evolution of the fractional species over time (Figure 1).
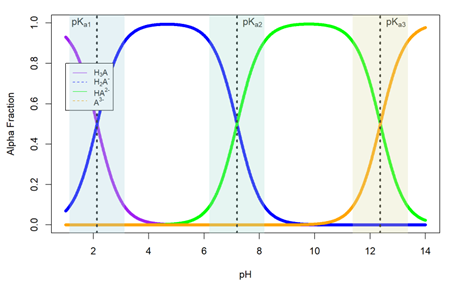
With each step of the acid dissociation of a polyprotic acid creating a pair of conjugate acid and base, we now have multiple opportunities to make buffer solutions with them. To make a buffer solution using a polyprotic acid system, you need to first decide on which buffer system among the multistep dissociation you use. As a rule of thumb, buffers usually work well within ±1 pH unit about the pKa of an acid; thus, we can make an effective buffer solution when the target pH is within 1 pH unit of the pKa of the conjugate acid. Now we have several H-H equations that can be used to calculate the pH values of the buffer solutions made from polyprotic acids/bases. For example, a triprotic system includes:
| [latex]pH = pK_{a_1} + \log \dfrac{[H_2A^-]}{[H_3A]} [/latex] | (8) |
| [latex]pH = pK_{a_2} + \log \dfrac{[HA^{2-}]}{[H_2A^-]} [/latex] | (9) |
| [latex]pH = pK_{a_3} + \log \dfrac{[A^{3-}]}{[HA^{2-}]} [/latex] | (10) |
Note that all three H-H equations hold true for any buffer solutions at any time, but you will find that it is more convenient to use the equation with a pKa closest to the target pH of the buffer solution to calculate the pH using the concentrations of the conjugate acid and base. (If you look at the α-plot above, you will see the multiple buffer regions around the pKa where the fractions of the conjugate acid/base species change from 0.1 to 1 and cross over each other).
When we prepare buffers to reach these targeted buffer systems, again, we could directly mix the conjugate acid and its conjugate base, or we could start with the acid and react with a strong base (such as NaOH) or start with the base and react with strong acid (such as HCl). The process is not more difficult than the process to make a buffer using a simple monoprotic acid/base, but it is important to consider the formation of new species that were not originally components of the buffer system (i.e., generating H2A when working with a buffer of HA¯ and A2-). The most important thing is to remember which buffer system you are trying to go to and keep track of how far you have gone in the polyprotic system (for example, by visualizing the α-plot).
However, before we can proceed with the experiments that compare the experimentally measured pH values of buffers with our predicted values, we need to introduce the concept of activity. The pH of a solution is measured with a pH meter. This meter measures the activity of hydronium ion (H+) instead of the TRUE concentration [H+]. Therefore, the pH measured is actually:
| pH = -logAH+ = -log([H+]γH+) | (11) |
Where γ is defined as the activity coefficient of the hydronium ion and is determined by the Davies equation:
| [latex]-\log \gamma_z = 0.51 z^2 \left[ \dfrac{\sqrt{\mu}}{1 + \sqrt{\mu}} - 0.3 \mu \right][/latex] | (12) |
In the equation above z is the charge of the ion of interest (1 for H+), and μ is the ionic strength of the solution defined as:
| μ = ½ * ∑ Ci zi2 | (13) |
The ionic strength considers the contributions of all ionic species C (in units of molarity, M), with a charge z. Consider a 1.0 M solution of NaCl. Sodium chloride completely dissociates to form Na+ and Cl- ions. Both species are present in a concentration of 1.0 M. To calculate the ionic strength:
| μ = ½ [12(1.0) + (-1)2(1.0 )] = 1.0 (M) | (14) |
Only when the ionic strength approaches 0 is it accurate to ignore an activity correction to your pH measurement. If you have charged species in solution, your measured pH will be different from the theoretical pH if you do not account for the ionic strength.
Another concept that will be explored in this lab is buffer capacity. Buffer capacity (β) is the measure of how well a buffered solution resists changes in pH when a strong acid or base is added. Mathematically, the buffer capacity is defined as:
| [latex]\beta = \dfrac{dC_{base}}{dpH} = -\dfrac{dC_{acid}}{dpH} = \dfrac{(number\;of\;moles\;of\;OH^-\;or\;H^+\;added\;per\;liter)}{pH\;change}[/latex] | (15) |
Buffer capacity is expressed in millimoles of strong acid or base only, and the per L per pH unit is assumed. If it helps you to think about the buffer capacity more clearly, you may include the units of L and pH in your reporting. The buffer capacity is at a maximum (for both the addition of a strong acid and base) when the pH = pKa. Consider the H-H equation explained previously and convince yourself that this is true.
Remember, as a rule of thumb, buffers usually work well within ±1 pH unit about the pKa of an acid because a buffer has the maximum buffer capacity (for both the addition of a strong acid and base) at the pH = pKa of the buffer system. When choosing a buffer system for a particular purpose, it is important to choose systems where the pKa is close (comfortably within +/- 1) of the target pH. It is also important that the chemicals you choose will not participate in other chemistries in solution that will interfere with the experiment you are trying to design.

Lab Concept Video
click here to hide the video (for printing purpose).
Write down observations or notes from the video in your lab notebook.
Pre-lab Work

Lab Skills
Review these lab skills videos prior to lab.
click here to hide the video playlist (for printing purpose).
Key Takeaways
- Using glassware to make precise measurements will be critical to your ability to calculate the buffer capacity of your solutions.
- Make sure you are writing down the species you are measuring and include all the digits displayed on the balance to get the most accurate calculation of the expected pH.
Extra Resources:

Prelaboratory Exercises
Find the day of the month of your birthday in Table 1 below. This is the buffer system you will prepare and study.
- Equation (3) in the introduction text represents the general case for the dissociation reaction of a triprotic acid across the pH spectrum range. In this experiment we will explore the buffering capabilities of phosphoric acid (H3PO4). In your laboratory notebooks, write the equilibrium expression for each of the acid dissociation reactions. Include the numerical value of the acid dissociation constant in your responses. HINT: Check out your textbook or Figure 1 for the information about numerical values for these dissociation constants!
- Calculate the grams of solid base and solid conjugate acid needed to prepare 100 mL of a high-capacity buffer solution. The buffer should be planned so that it has 0.10 M conjugate acid and will fulfill H-H equation for the target pH. Do not use activity coefficients in this planning. To check your calculations and planning with your laboratory instructor, submit your (a) birthday, (b) calculated amount (grams) of acid, and (c) calculated amount (grams) of conjugate base to the Google Form BEFORE THE BEGINNING OF YOUR SCHEDULED LABORATORY PERIOD. Note that these amounts are ESTIMATES of what you should weigh out when preparing the buffers in lab. Be sure to record the ACTUAL weights (capture the full significant figures from the balance) of the salts used, as well as noting the exact molecular formula from the bottles you took the salts from.
- Calculate the grams of just the base of your conjugate pair necessary to make a 100 mL 0.1 M solution. You will need this solution for Step 9 of the experimental procedure below. Predict whether this solution of only the base species of your system will have a higher or lower pH. Explain your answer.
- Consider a 1 L solution of 0.05 M sodium formate (HCO2¯; pKa (HCO2H) = 3.744). What is the final pH (do not consider an activity correction) after adding 12 mL of 1.0 M HCl?
- Now calculate what the pH meter will read for the problem described in question 4. Comment on the % difference between what would be measured vs. was calculated.
| Birthday | System | pH | |
| 1, 17 | NaH2PO4 · H2O | Na2HPO4 · 12H2O | 6.6 |
| 2, 18 | NaH2PO4 · H2O | K2HPO4 | 6.7 |
| 3, 19 | NaH2PO4 · 2H2O | K2HPO4 | 6.8 |
| 4, 20 | KH2PO4 | K2HPO4 | 6.9 |
| 5, 21 | NaH2PO4 · 2H2O | Na2HPO4 · 12H2O | 7 |
| 6, 22 | NaH2PO4 · H2O | K2HPO4 · 3H2O | 7.1 |
| 7, 23 | NaH2PO4 · 2H2O | K2HPO4 · 3H2O | 7.2 |
| 8, 24 | KH2PO4 | K2HPO4 · 3H2O | 7 |
| 9, 25 | KH2PO4 | Na2HPO4 · 12H2O | 7.3 |
| 10, 26 | NaH2PO4 · H2O | Na2HPO4 · 12H2O | 7.4 |
| 11, 27 | NaH2PO4 · 2H2O | Na2HPO4 | 7.5 |
| 12, 28 | KH2PO4 | Na2HPO4 | 7.1 |
| 13, 29 | KH2PO4 | Na2HPO4 · 12H2O | 7.6 |
| 14, 30 | NaH2PO4 · H2O | Na2HPO4 · 7H2O | 7.7 |
| 15, 31 | NaH2PO4 · 2H2O | Na2HPO4 · 7H2O | 7.2 |
| 16 | KH2PO4 | Na2HPO4 · 7H2O | 7.8 |

Before You Take The Quiz on Canvas
- Know the Henderson-Hasselbalch equation and how it applies to buffer systems.
- Be able to calculate the concentration of one of the conjugate species given a target pH of a buffer solution (neglecting activity).
- Be able to calculate ionic strength given the components and concentration of a solution.
- Be able to calculate activity coefficients using the Davies equation.
- Know how to account for activity in the Henderson-Hasselbalch equation.
- Be able to calculate the buffer capacity of a buffer given a set of raw data—initial pH of the buffer and the pH of the buffer after the addition of a known amount of HCl (or NaOH).

Experimental
- Highest capacity buffer. Plan and prepare 100 mL of buffer solution. The buffer should be planned so that it is 0.10 molar in conjugate acid and at the requested pH. Do not use activity coefficients in this planning. Check your calculations by using this Google Form.
- Medium capacity buffer. Dilute 10 mL of your high-capacity buffer to 100 mL with deionized water. Note the concentration of the buffer in your laboratory notebook.
- Low-capacity buffer. Dilute 10 mL of your medium-capacity buffer to 100 mL with deionized water. Note the concentration of the buffer in your laboratory notebook.
- Measure out 40 mL of each of the three buffers using a graduated cylinder and place each in its own 50 mL beaker. Standardize a pH meter and measure the pH of each of these 3 buffers.
- Add 1.00 mL of 0.10 M HCl to each of the three buffers. Mix well and measure the pH.
- Place 40 mL of each of the three buffers each in its own 50 mL beaker. Add 1.00 mL of 0.10 M NaOH. Mix well and measure the pH.
- Place 40 mL of deionized water in a 50 mL beaker. Measure its pH. Add 1.00 mL of 0.10 M HCl, mix well and then measure the pH.
- Repeat #7 but add NaOH instead of HCl.
- A more common practice for making a buffer is to begin with an acid or base, usually a salt, that is one-half of the conjugate pair necessary for creating the desired buffer. Then either strong acid or base is used to adjust the pH to the desired value. Make the solution described in Question 3 of the prelaboratory exercise. Pour this solution in a 400 mL beaker and insert the pH probe in the solution using a ring stand and clamp apparatus. Fill your buret with 0.5 M HCl. Use a stir bar to assist with mixing your solution but ensure the stir bar does not hit the pH probe in your set up. Measure the volume of HCl added to achieve the target pH and record the result in your notebook.
Post-Lab Work Up

Results/Calculations
Fill out the answer sheet for this experiment completely. Answer the following post-lab questions.
- How closely does your experimentally determined pH agree with your planned value? Only consider the result on the buffer of highest capacity.
- Using activity coefficients, estimate the pH value for the buffer of highest capacity. How closely does your experimentally determined pH value agree with this more refined value?
- Calculate the buffer capacity of each of your three buffer solutions. Buffer capacity is expressed in millimoles of strong acid or base only, and the per L per pH unit is assumed. If it helps you to think about the buffer capacity more clearly, you may include the units of L and pH in your reporting. You may assume linear behavior for the change in pH verses the amount of acid or base added.
- Calculate the concentrations of the conjugate acid and base pair at the target pH, which you achieved by adding 0.5 M HCl quantitatively in Step 9 of the procedure (no need to include activities in this case). Assume at VHCl=0 only the base form exists in solution. Recall that upon addition of the strong acid, the weak base will fully convert to the conjugate acid species. Compare the ratio of species in the Henderson-Hasselbach equation (the term [A−]/[HA]) for the buffer prepared in Step 9 (at the target pH) to the predicted ratio you calculated in Question 2 of the prelaboratory exercise. Provide an explanation for similarities or differences you observe.

Challenge Questions
Challenge questions are designed to make you think deeper about the concepts you learned in this lab. There may be multiple answers to these questions! Any honest effort at answering the questions will be rewarded.
- In the prelaboratory assignment, you used the Henderson-Hasselbalch equation to determine how much of each salt was needed to achieve the target pH. Is it possible to use the H-H equation to predict the pH of a solution made only with the basic form of the pair? Explain your answer.
- Suppose a work colleague asks your advice about using the phosphoric acid system for making a pH of 9.0 buffer. Assuming there are no interfering reactions to worry about, what would your recommendation be for using the phosphoric acid system for their application? Are there other, more suitable systems that might work better? Be sure to justify your answer.
- If we would like to make a 1 L buffer solution with 0.1 M concentration with a pH value of 7.0 using KH2PO4 and K3PO4, how many grams of each reagent do we need?
- If we need to make a buffer solution with a pH = 7.0 by adding 1 M HCl solution to a 1 L solution of 0.1 M K3PO4, how many mL of HCl do we need to add? Describe the chemistry that would take place in the flask as you add the HCl.

Lab Report Submission Details
Submit your lab report on Canvas as 1 combined PDF file. This submission should include:
- The completed answer sheet.
- Your lab notebook pages associated with this lab, which should include answers to the post-lab questions and challenge questions.
The grading rubric can be found on Canvas.
- Moran, L., Scrimgeour, K. G., Horton, R. H., Ochs, R. S., Rawn, D. J., Biochemistry 2nd Ed., Prentice Hall, NJ, page 318.
- Harris, D. C. & Lucy, C. A. Quantitative Chemical Analysis, 10th ed.; W. H. Freeman: New York, NY, 2020
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please ask your instructor or TA.)
