Elements and Their Interactions
We now move on to consider the macroscopic behavior of atoms, that is, the behaviors of very, very large numbers of atoms that form the materials that we touch, feel, smell, and observe with our own eyes. Before we do that, it is important to understand and be explicit about what properties atoms, molecules, and their aggregates can and cannot exhibit.
Elements and Bonding
When atoms interact with one another to form molecules or larger structures, the molecules have different properties than their component atoms; they display what are often referred to as emergent properties, where the whole is more than, or different from the sum of its parts. In a similar way groups of atoms or molecules have different properties from isolated atoms/molecules. For example while groups of atoms/molecules exist in solid, liquid, or gaseous states, and often have distinct colors and other properties, isolated atoms/molecules do not; there are no solid or liquid isolated atoms and they do not have a color or a boiling point. So the obvious question is, how many atoms or molecules need to aggregate before they display these emergent properties, before they have a color, before they have a melting point, boiling point, heat capacity, and other properties that isolated atoms do not? The answer is not completely simple, as you are probably slowly coming to expect. As we add more and more atoms or molecules together their properties change but not all at once. You have probably heard about nanoscience and nanotechnologies, which have been the focus of a great deal of research and economic interest in the past decade or so. Nanoparticles are generally classified as being between 1 and 100 nm in diameter (a nanometer is one billionth of a meter or 1 × 10–9 m). Such particles often have properties that are different from those of bulk (macroscopic) materials. Nanomaterials can be thought of as a bridge between the atomic-molecular and macroscopic scales.

Assuming that they are pure, macroscopic materials have predictable properties and it doesn’t really matter the size of the sample. A macroscopic sample of pure gold behaves the same regardless of its size and if Archimedes (ca. 287–212 bce) were alive today, he could tell you whether it was pure or not based on its properties, for example, its density. But gold nanoparticles have different properties depending upon their exact size. For example, when suspended in water, they produce colors ranging from orange to purple, depending on their diameter (see Figure). Often the differences in the properties displayed are due to differences in the ratio of surface area to volume, which implies that intermolecular forces (forces between molecules) are more important for nanomaterials. As we cluster more and more particles together, the properties of the particles change. Biomolecules generally fall into the size range of nanomaterials, and as we will see their surface properties are very important in determining their behavior.
Unfortunately when we are talking about the properties of atoms and molecules versus substances and compounds, it can be difficult, even for experienced chemists, to keep the differences clear. In addition different representations are often used for different organizational levels; it is an important skill to be able to recognize and translate between levels. We will be using a range of representations to picture atoms and molecules; chemists (and we) typically use various shorthand rules, methods, and chemical equations to represent molecular composition, shape, and behaviors. But just knowing the equations, often the only thing learned in introductory chemistry courses, is not sufficient to understand chemistry and the behavior of atoms and molecules. Much of the information implied by even the simplest chemical equations can easily be missed—or misunderstood—if the reader does not also have a mental picture of what the diagram or equation represents, how a molecule is organized and its shape, and how it is reorganized during a particular reaction. We will be trying to help you get these broader pictures, which should you make sense of the diagrams and equations used here. That said, it is always important to try to explicitly identify what you are assuming when you approach a particular chemical system; that way you can go back and check whether your assumptions are correct.
“From the 115 elements you can build a near infinity of molecules, of any type you need, to get all the structural and functional diversity you can ask for. There are at least 100,000 different molecules in the human body. Some 900 volatile aroma components have been found in wine. Chemistry is molecules. We are molecules. Chemistry is a truly anthropic science.”
–Roald Hoffman (1937) quoted by Natalie Angier in The Canon
By this point, you probably have some idea or mental image of the basic (low resolution) structure of atoms. We will therefore return to some questions left unanswered. Why is it that two hydrogen atoms form a strong stable (covalent) bond, a bond that requires temperatures above 5000 K to break, whereas two helium atoms and two hydrogen molecules have only a weak (London dispersion forces) attraction for each other that is broken at very low temperatures (4–20 K)? Because temperature is a measure of the kinetic energy present in the system we have to ask, what gives rise to this huge difference? Is there something fundamentally different going on in these situations? Other potentially troubling questions may also come to mind, in particular, how can pure samples of different elements be so different? Why is carbon either black (graphite) or transparent (diamond)? Why is gold shiny and yellow, while sulfur is dull and yellow? Why are most metals, but not gold or copper, shiny, solid, and colorless, while mercury is shiny, colorless, and liquid? Why are some elements more or less inert (such as gold, which does not tarnish) while others, such as iron (which rusts) and phosphorus (which bursts into flames) are highly reactive? To answer these questions will lead to an understanding of the basics of chemistry or how atoms interact with one another under various conditions. We will approach the answers in a step-by-step manner. In some cases where the answers are very complex (as is the case for why gold is yellow and mercury is a liquid), we will sketch out the answer but probably not provide a satisfying explanation. Luckily, most of the chemistry we need to address is not nearly so arcane!
Before we consider these and other questions, let us recap what we think we know about atoms and electrons. Most of an atom’s mass is localized in a very small region, the nucleus, surrounded by electrons that occupy most of the volume of the atom. Electrons have a number of strange properties because they are quantum mechanical particles. This means that under some conditions their behavior is best described by considering them as negatively charged particles, and under other conditions it is more helpful to consider them as waves; they are really both (and neither). Because of the uncertainty principle when we know the energy of each electron rather accurately we do not (and cannot) know where, exactly, a particular electron is at a particular moment in time. In fact, because all electrons are identical, if we had two electrons and turned away from them we could not tell which was which when we turned back. Within an atom each electron has a discrete energy and is characterized by its set of quantum numbers; no two electrons in an atom have the same set of quantum numbers. Perhaps you will be disappointed (or perhaps pleased) to know that a rigorous quantum mechanical (and relativistic) treatment of atoms and their interactions is beyond the scope of this book.[1] That said, we can give a reasonable overview of how the behavior of atoms can be explained in terms of atomic and molecular electron orbitals. We will also indicate where our description is an over-simplification.
It is worth remembering that there are very few (if any) instances when we come across isolated atoms. Although we often describe matter as being composed of atoms, that is a bit of an abstraction; most atoms are stuck to other atoms by bonds and interactions. As mentioned previously, this leads to emergent properties that are quite distinct from those of the isolated atoms of which they are composed. It is the interactions between atoms and molecules that makes surfaces solid.
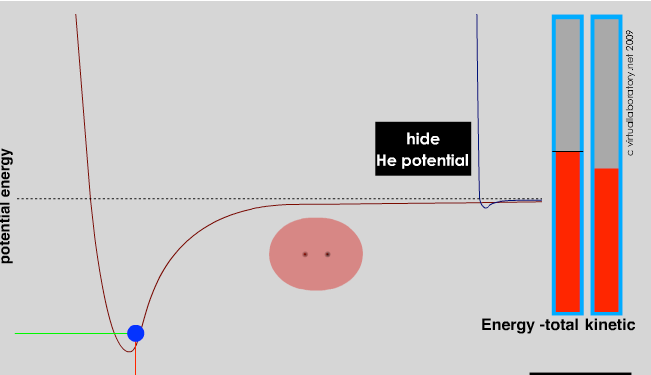
If isolated atoms are rare, the obvious question is, why are they rare? What determines when and how atoms interact? The answer is simple really and based on a principle we have already encountered (and that we will return to time and again): systems will adopt the lowest energy state accessible to them. The reason is that at the lowest accessible energy state, the forces of attraction and repulsion are equilibrated. It would take more energy to move the components of the system (that is atoms in molecules, or electrons in atoms) because the forces acting on them would increase. Interactions and bond formation lead to lower potential energy. Whether the bonded system is stable will then depend upon the strength of the interaction/bond and the forces that impact the molecule. For example, surrounding molecules/atoms with a range of kinetic energies may collide with the molecule. If this kinetic energy of the impacting particle is larger than the interaction/bond energy, the collision can disrupt the interaction or break the bond(s) between them; if not, the interaction/bond will be stable. At the same time, there must be overarching principles governing which interactions occur and which do not; otherwise everything would clump together, which would be messy and not particularly interesting. These principles arise from the way electrons are organized in different types of atoms.
Thinking about the nature of the chemical bond: Molecular Orbitals
There is no single explanation that captures all the properties observed when atoms interact to form a bond.[2] Instead we use a range of models of bonding. Now, what do we mean by model? Models are much more limited than theories, which have global application and can be proven wrong through observation and experimental data. Models are more like strategies that simplify working with and making predictions about complex systems. A model often applies to only very specific situations. For example the Bohr model of the atom applies only to hydrogen and then only under quite specific circumstances. We are going to consider a variety of bonding models, some of which you may already be familiar with, but it is important that you remember that different models are used depending upon which properties you want to predict and explain.
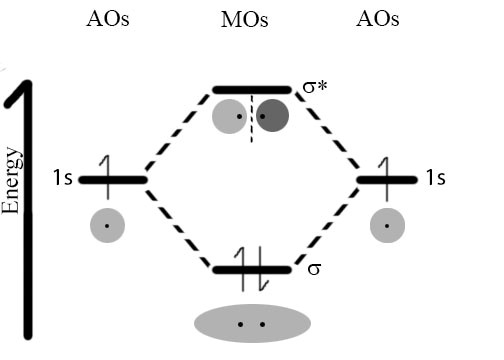
So back to our original dilemma, namely why is it that the interaction between two hydrogen atoms is so much stronger than that between two helium atoms? One useful model of bonding uses the idea that electrons can be described in terms of orbitals.[3] Each orbital can contain a maximum of two electrons (with opposite spins). Recall that in an isolated atom, the electrons are described by atomic orbitals; therefore when in molecules, they are described by molecular orbitals (MOs). When atoms approach each other, the atomic orbitals containing their outermost electrons, known as the valence electrons, begin to interact. Because of the wavelike nature of the electron, these interactions can be either constructive or destructive. If they interact in a constructive manner, the interaction is stabilizing, which means that potential energy decreases and (if that energy is released into the surrounding system) the two atoms adopt a more stable configuration; they form a bond that holds them together. If the interaction is destructive, there is no stabilizing interaction. In the case of hydrogen each atom has a single (1s) orbital occupied by a single electron. As the atoms approach one another these 1s atomic orbitals interact to form two possible MOs: a lower energy, constructive or bonding MO, and a higher energy, destructive or anti-bonding MO. Notice that the bonding MO, a so-called σ1s (sigma) orbital, has electron density (that is a high probability that the electrons would be found there if we looked) between the two hydrogen nuclei. In the anti-bonding MO, known as σ*1s, the electrons are mostly not between the nuclei. One way to think about this is that in the bonding orbital the protons in the hydrogen nuclei are attracting both electrons (one from each atom) and it is this common attractive force between electrons and nuclei that holds the two hydrogen atoms together. In contrast in the anti-bonding orbital there is little electron density between the two nuclei and any electrons in that orbital are actually destabilizing the system by enhancing the repulsive interactions between the nuclei. (Can you provide a short reason why this would be the case?)
Just like an atomic orbital each MO, both bonding and anti-bonding, can hold two electrons. In the case of two approaching hydrogens there are only two electrons present in the system and the lowest energy state would have them both in the bonding orbital. Typically, both electrons in a H–H molecule are found in the lower energy (more stable) σ1s bonding orbital. This arrangement of electrons is referred to as a covalent bond; this is the arrangement that requires temperatures of ~5000 K to break, which means it requires a lot of energy to break a covalent bond.
Now let us take a look at what happens when two helium atoms approach. Each He atom has two electrons in its 1s orbital. As the orbitals approach they interact and again produce two MOs, the bonding σ1s orbital and the anti-bonding σ*1s orbital. The σ*1s MO has no electron density between the two He nuclei and has considerably higher energy than the atomic orbitals of the isolated atoms. Since there are 4 electrons present in the two He atoms and only two can occupy the σ1s bonding orbital; the other two have to go into the σ*1s anti-bonding orbital. The end result is that the decrease in potential energy (increased stability) associated with occupying the bonding orbital is more than off-set by the increased energy associated with occupying the σ*1s anti-bonding orbital. So, the end result is no overall stabilization and no decrease in energy associated with bond formation; no covalent bond is formed. The only interactions between helium atoms are the van der Waals interactions that occur between the two atoms that depend exclusively on London dispersion forces.
The interaction between two helium atoms is very similar to that between two H2 molecules. There is no possibility of stabilizing MOs forming and, as in the case of the helium atoms, hydrogen molecules (H–H or H2) interact exclusively through London dispersion forces (LDFs). The LDFs will be somewhat stronger between hydrogen molecules than between helium atoms, however, because there is a larger surface area over which they can interact.
The idea that—all other things being equal—a system will move to the lowest accessible energy state (losing the excess energy to their surroundings), where the forces of attraction and repulsion are equal, is applicable to a wide range of situations. The potential energy of the system falls as the distance between the atoms decreases until the system reaches a balance between the stabilizing interaction of bond formation and the destabilizing repulsion of the two nuclei. The energy difference between the separated atoms and the minimum energy is called the bond energy and this amount of energy must be supplied to the system to break the two atoms apart again. The distance between the nuclei when the bond energy is at its minimum is the bond length. When a bond is formed between two atoms energy is always released to the surroundings and the new material is always more stable than the two separate atoms. Because energy is conserved a bond cannot form unless this bond energy is transferred from the interacting atoms to the rest of the system (usually by colliding with other atoms and transferring energy). Making bonds is always exothermic (meaning that energy is released not absorbed). This implies that energy (from the surrounding system) is always needed to break a bond. To break a bond energy must be transferred from the surroundings. Bond breaking is endothermic meaning it requires energy from the external world, normally delivered through collisions with other molecules.
When we consider more complex chemical reactions we will find that these generally involve both bond breaking and bond formation; the overall reaction will be exothermic when more energy is released from bond formation than is used for bond breaking. Conversely a reaction is endothermic (that is, uses energy) if more energy is required to break bonds than is released in bond formation. The important point is that we have to consider the system as a whole, including all of the bonds formed and broken. We will come back to this topic later.
Discrete Versus Continuous Molecules
Having considered the bonding situation with hydrogen and helium, the simplest two elements, we can now move on to consider other elements and the types of molecules that they form. In this discussion, we begin with molecules made up of a single type of atom. More complex molecules made of atoms of multiple elements will be considered later. As the number of protons in the nucleus of an element’s atoms increases, from 1 in hydrogen to 10 in neon, we find dramatic changes in physical properties that correlate with whether the elemental form is discrete or continuous. The discrete forms are either monoatomic—meaning that they exist as separate atoms (such as He and Ne) with no covalent bonds between them (although they do interact via van der Waals interactions)—or diatomic molecules (such as H2, N2, O2, and F2), meaning that they exist as molecules that have only two atoms. The elements that exist as small molecules have very low melting points (the temperatures at which they change from a solid to a liquid) and low boiling points (the temperatures at which they change from a liquid to a gas). But don’t confuse these phase transitions with the breaking of a diatomic molecule into separate atoms. Phase transitions, which we will discuss in greater detail later, involve disruption of interactions between molecules (intermolecular forces), such as London dispersion forces, rather than interactions within molecules, that is, covalent bonds.
| Elemental Form | Melting Point | Boiling Point | Bp-Mp (*) | Name |
| H2 molecular | 13.81 K | 20.28 K | 6.47 K | hydrogen |
| He atomic | 0.00 K | 4.22 K | 3.27 K | helium |
| Li continuous | 453.65 K | 1615 K | 1161 K | Lithium |
| Be continuous | 1560 K | 2744 K | 1184 K | beryllium |
| B continuous | 2348 K | 4273 K | 1925 K | boron |
| C continuous | 3823 K | 4098 K | 275 K | carbon |
| N2 molecular | 63.15 K | 77.36 K | 14.21 K | nitrogen |
| O2 molecular | 54.36 K | 90.20 K | 35.84 K | oxygen |
| F2 molecular | 53.53 K | 85.03 K | 31.5 K | fluorine |
| Ne atomic | 24.56 K | 27.07 K | 2.51 K | neon |
In contrast to the elements that form discrete molecules, the atoms of the other elements we are considering (that is Li, Be, B, C) interact with one another in a continuous manner. Rather than forming discrete molecules, these elements can form ensembles of atoms in which the number of atoms can range from the small (a few billion) to the astronomical (very, very large). Whether the materials are at the nano- or the macroscopic levels, the atoms in these ensembles are held together by bonds that are very difficult to break, like the bond in H–H. That is, a lot of energy must be put into the system to separate the component atoms. However, unlike hydrogen, the atoms that form these structures must form bonds with more than one other atom.
A consequence of this difference in organization is a dramatic increase in both the melting and boiling points compared to atomic (He, Ne) and molecular (H2, N2, O2, and F2) species (Table 3.1). The reason is that when a substance changes from solid to liquid (at the melting point) the component particles have to be able to move relative to one another. When the substance changes from a liquid to a gas (at the boiling point) the particles have to separate entirely. Consequently the magnitude of the melting and boiling points gives us a relative estimate of how strongly the particles are held together in the solid and liquid states. As we have already seen temperature is a measure of the average kinetic energy of the molecules in a system. For elements that exist as discrete atoms or molecules the only forces that are holding these particles together are London dispersion forces, which are relatively weak compared to covalent bonds. In contrast, the elements that exist as extensive networks of atoms joined by bonds require much more energy to break as the material goes from solid to liquid to gas.
Questions
Questions to ponder
- Are all bonds the same?
- What factors might influence bond strength?
- Why are the properties of atoms and molecules different?
Questions to Answer
- Where are the electrons in H2 when the temperature is greater than 5000 K?
- What would happen if you could form a He–He system with 3 electrons (instead of 4)?
- What would a molecular-level picture of H2 (g) look like?
- What would a molecular-level picture of H (g) look like?
- Where does the energy to break a bond come from?
- Where does the energy released upon bond formation go?
- The melting point of molecular hydrogen (H2) is ~14 K (-259 °C). Draw a molecular level picture of what molecular hydrogen looks like below this temperature (as a solid). Why are the molecules of hydrogen sticking together?
- The boiling point of molecular hydrogen (H2) is ~20 K (-253 °C). Draw a molecular level picture of what molecular hydrogen looks like above this temperature (as a gas).
- Molecular hydrogen dissociates at high temperatures (> 6000 K). Draw a picture of what you imagine this might look like. Why do you think it takes such a high temperature to bring about this change?
Metals
 Metals have quite a wide range of properties at normal temperatures, from liquid (like mercury) to extremely hard (like tungsten). Most are shiny but not all are colorless. For example gold and copper have distinct colors. All metals conduct electricity but not all equally. How can we explain all these properties? Let us use aluminum (Al) as an example because most of us have something made of aluminum such as a pan or aluminum foil. With modern instrumentation it is quite easy to visualize atoms and a variety of techniques have been used to image where the aluminum atoms are in the solid structure. What emerges is a picture of aluminum nuclei and their core electrons, packed like spheres where one layer of spheres rests in the interstices of the underlying and overlying layers; where the positions of the electrons are within this structure not well defined.
Metals have quite a wide range of properties at normal temperatures, from liquid (like mercury) to extremely hard (like tungsten). Most are shiny but not all are colorless. For example gold and copper have distinct colors. All metals conduct electricity but not all equally. How can we explain all these properties? Let us use aluminum (Al) as an example because most of us have something made of aluminum such as a pan or aluminum foil. With modern instrumentation it is quite easy to visualize atoms and a variety of techniques have been used to image where the aluminum atoms are in the solid structure. What emerges is a picture of aluminum nuclei and their core electrons, packed like spheres where one layer of spheres rests in the interstices of the underlying and overlying layers; where the positions of the electrons are within this structure not well defined.
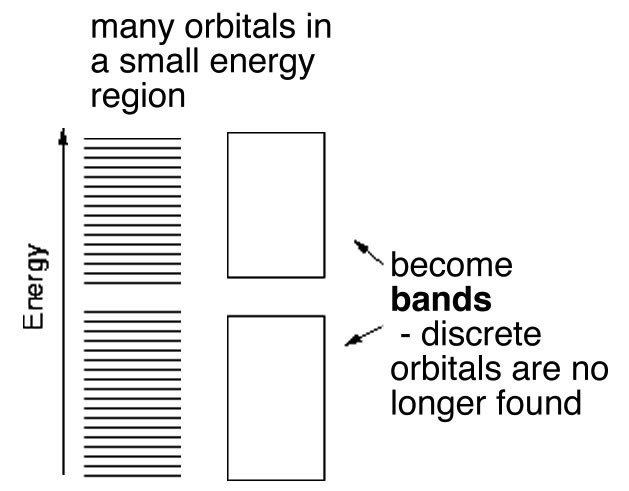
In H–H or diamond the electrons involved in bonding are located (most probably) between the two nuclei. In contrast in aluminum and other metals the valence electrons are not closely associated with each nucleus. Instead they are dispersed over the whole macroscopic piece of metal. Imagine that instead of two or three or four atomic orbitals combining to form MOs, a mole (6 × 1023) of atomic orbitals were combined to produce a mole of MOs. As more and more MOs are formed the energies between them gets smaller and smaller. For a macroscopic piece of metal (one you can see) the energy gap between the individual bonding MOs will be negligible for all intents and purposes. These orbitals produce what is essentially a continuous band of (low-energy) bonding MOs and a continuous band of (higher-energy) anti-bonding MOs. The energy gap between the bonding and anti-bonding orbitals is called the band-gap and in a metal this band-gap is quite small (recall that the gap between the bonding and anti-bonding MOs in diamond is very large). Moreover in metals the bonding MOs (known as the valence band) are able to accommodate more electrons. This is because in metals there are typically fewer electrons than there are atomic orbitals. Consider aluminum: it has three valence electrons and in the ground (lowest energy) state has an electron configuration of 3s23p1. This suggests that it has two unoccupied 3p orbitals. We can consider the bonding MOs in aluminum to be formed from all the available atomic orbitals, which means that there are many bonding MOs that are not occupied by electrons. The physical consequences of this are that the valence electrons can move relatively easily from one MO to another because their energies are very close together. Whereas nuclei and core electrons remain more or less locked in position the valence electrons can spread out to form a kind of electron sea within the metal. When an electrical potential is applied across the metal, electrons from an external source can easily enter the valence band and electrons can just as easily leave the metal. Electrical conductivity is essentially a measure of how easily electrons can flow through a substance. Metals typically have high conductivity due to the ease with which electrons can move from one MO to another and the fact that each MO extends throughout the whole piece of metal. Because the numbers of electrons entering and leaving are the same, the piece of metal remains uncharged.
In this model the atomic cores are packed together and surrounded by a cloud of electrons that serve as the “glue” that binds them together. There are no discrete bonds in this type of structure. When a piece of metal is put under physical stress (for example it is stretched or deformed) the atoms can move relative to one another but the electrons remain spread throughout the structure. Metals can often be slowly deformed into different shapes without losing their structural integrity or electrical conductivity—they are malleable! They can be melted (increased atomic movement), become liquid, and then allowed to cool until they solidify; throughout this process they retain their integrity and their metallic properties and so continue to conduct electricity.[4] This is quite different from how other substances (such as diamond or water) behave. The hardness of a solid metal depends on how well its atoms packed together and how many electrons are contributed to the valence band of orbitals.
So why do some elements behave as metals and others do not? For example graphite conducts electricity but it is not malleable and can’t be heated and molded into other shapes. The answer lies in the behavior of the MOs and the resulting bonds they can produce. Graphite has a rigid backbone of carbon–carbon bonds that makes it strong and stable but overlaying those bonds is the set of delocalized MOs that spread out over the whole sheet. As a result graphite has some properties that are similar to diamond (stability and strength), some that are similar to metals (electrical conductivity), and some that are a consequence of its unique sheet structure (slipperiness).
Why Are Metals Shiny?
We see things because photons hit the back of our retinas and are absorbed by specialized molecules (proteins and associated pigment molecules). This leads to changes in protein structure and initiates a cascade of neuron-based cellular events that alters brain activity. So where do these photons come from? First and foremost they can be emitted from a source (the Sun, a light bulb, etc.) that appears to shine and can be seen in the dark. Alternatively, photons can be reflected off a surface; in fact most of the things we see do not emit light, but rather reflect it. A red T-shirt appears red because it absorbs other colors and reflects red light. Photons can also be refracted when they pass through a substance. A cut diamond sparkles because light is refracted as it passes through the material and exits from the many facets. Refraction is caused when photons bump into electrons, are absorbed, and then (very shortly thereafter) are re-emitted as they travel through a material. These processes take time, so the apparent speed of light slows down. It can take a photon many thousands of years to move from the core to the surface of the Sun because of all the collisions that it makes during the journey.[5]
To explain why metals (and graphite) are shiny, we invoke a combination of reflection, refraction, and the energy levels of MOs. When a photon of light is absorbed and reemitted, the electron moves from one orbital to another. Let us consider a piece of metal at room temperature. When a photon arrives at the metal’s surface it encounters the almost continuous band of MOs. Most photons, regardless of their wavelength, can be absorbed because there is an energy gap between orbitals corresponding to the energy of the photon. This process promotes electrons up to a higher energy level. As the electrons drop back down to a lower energy level, the photons are re-emitted, resulting in the characteristic metallic luster. Metals actually emit light, although this does not mean metals glow in the dark (like a light bulb or the Sun). Instead, metals absorb and re-emit photons, even at room temperature.
The color of a particular metal depends upon the range of wavelengths that are re-emitted. For most metals the photons re-emitted have a wide range of wavelengths which makes the metallic surface silvery. A few metals, such as copper and gold, absorb light in the blue region and re-emit light with wavelengths that are biased toward the red end region of the spectrum (400–700 nm) and therefore they appear yellowish. This is due to relativistic effects way beyond the scope of this book, but something to look forward to in your future physical chemistry studies!
Now we can also understand why metals emit light when they are heated. The kinetic energy of the atoms increases with temperature which promotes electrons from low to higher energy orbitals. When these electrons lose that energy by returning to the ground state, it is emitted as light. The higher the temperature the shorter the wavelength of the emitted light. As a filament heats up, it first glows red and then increasing whiter as photons of more and more wavelengths are emitted.
Questions
Questions to Answer
- What properties indicate that a substance is metallic?
- Why are metals shiny?
- How can metallic properties be explained by the atomic-molecular structure of Al (for example)?
- Why can we see through diamond but not aluminum? How about graphite?
- Why does aluminum (and for that matter all metals) conduct electricity? What must be happening at the atomic-molecular scale for this to occur?
- What does the fact that diamond doesn’t conduct electricity tell you about the bonding in diamond?
- How do the bonding models for diamond and graphite explain the differences in properties between diamond, graphite, and a metal like aluminum?
- Why is it OK to use different models to describe bonding in different species?
- For those who want more, rest assured that you will find out if you take more advanced classes either in physics or physical chemistry. ↵
- This study shows images of bonds forming http://www.sciencemag.org/content/340/6139/1434.abstract ↵
- Although perhaps the word orbital is confusing because it implies a circular or elliptical motion, what we mean is the volume in which there is a 90% probability of finding an electron. That said, orbitals are the way chemists (and the occasional physicist) talk, so we have to use it. ↵
- We need to mentions (at least) what electricity is, i.e. the flow of electrons. ↵
- Robert Naeye (1998). Through the Eyes of Hubble: Birth, Life and Violent Death of Stars. CRC Press. ISBN 0750304847. Of course this raises the question, is it the same photon? ↵

