Carbon: An Amazingly Allotropic Element

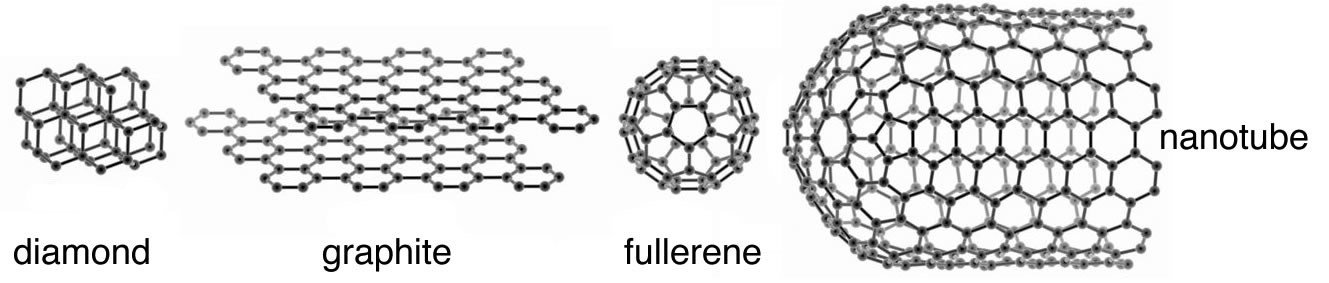
To give you an idea of some of the different types of bonds that form between elements, we are going to consider several representative elements from different areas of the periodic table. For starters, let us take a look at carbon. Carbon (C) belongs to the family of elements known as non-metals. The bonding between C atoms (and to other types of atoms) is typically described as covalent bonding where each bond involves two electrons (one from each of the bonded atoms). Although this is the most common model we will see that it is not the only possible one; we will introduce other models as they are needed. Diamond is the name given to one of the naturally occurring forms (known as allotropes) of pure C; the other allotropes of carbon are graphite, graphene, and various fullerenes, which we will return to later. The important question is: How can these substances have such different properties, yet be composed of the same types of atoms? For example: diamond is hard, colorless, sparkly and do not conduct electricity, but graphite is soft, grey, shiny, and does conduct electricity. The answer lies in the molecular level structure of these allotropes of carbon.

Diamonds form from carbon-rich materials subjected to very high pressure (45,000–60,000 atmospheres) but relatively low temperatures (900–1300 ºC).^[1] Such conditions can be found about 100 miles under the Earth’s crust, the region known as the lithosphere. Diamonds have also been found in asteroids, which originate from outside of the Earth. Diamonds are so valued because they are rare, sparkly, hard, and almost completely inert. It is very hard to make diamonds do anything at all except sit there and sparkle; they don’t dissolve in water and they melt only at very high temperatures (mp = 3330 °C). Diamond has the highest melting point of any known substance, so high that these measurements are actually done under high pressure and then calculated to estimate what the value would be at atmospheric pressure. In addition, when diamond is melted it decomposes. When it is heated in an atmosphere of oxygen it reacts to produce carbon dioxide; when oxygen is absent it transforms into graphite. There is no such thing as molten diamond. Diamonds are extremely hard (the hardest naturally occurring substance) and do not conduct electricity at all (as we will see, to conduct electricity, electrons must be able to flow through the material). This suggests that the molecular-level structure of diamond is quite different from that found in metals (which we will see are malleable and conduct electricity). Any useful model of diamond’s structure must explain how these properties arise from atomic interactions.

Let us step back and look at the properties of diamond and see if we can make sense of them. To be so stable (chemically inert) diamond must have very strong bonds that take a lot of energy to break. The fact that it does not conduct electricity indicates that the electrons must not be free to move around within a diamond. A polished diamond is sparkly because some light is reflected from the surface and some light passes through it, making it transparent. If the diamond were not cut with so many facets it would allow most light to pass through it.

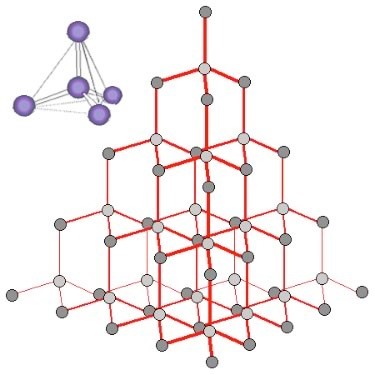
When we look at an X-ray diffraction-based structure^[2] of diamond we find that each carbon atom is surrounded by four other carbon atoms situated at equal distances and equal angles from each other. In this context, the most useful model of bonding involves thinking of each carbon atom as forming four covalent (electron-sharing) bonds, all arranged so that the electron pairs are as far apart as possible. This places the four bonded atoms at the corners of a tetrahedron, with a central carbon atom. Each of these corner atoms is itself at the center of a similar tetrahedron of carbons (see Figure). Experimental evidence indicates that all the bonds, bond lengths, and bond angles in diamond are identical; the C–C–C bond angles are ~109º. A diamond can be considered as one huge molecule connected by a network of carbon–carbon bonds.

How do we explain this arrangement in terms of what we know about the electronic structure of carbon atoms? The answer is that the electronic structure of the carbon atoms is reorganized to form bonding orbitals. In the case of carbon, each atom can form four bonding orbitals that are oriented as far apart as possible. There are several models to explain how this occurs, but it is important to remember that they are all models, designed to help us understand the properties of diamond.

The Hybrid Orbital Model

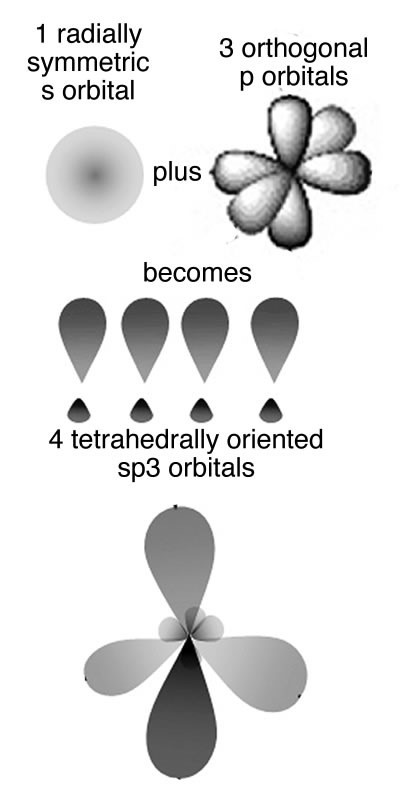
In this model the orbitals involved in carbon–carbon bonding are considered to be hybrids or mixtures of atomic orbitals. If carbon forms four bonds (and it does) then four bonding orbitals are needed. Carbon has available orbitals in the second (n = 2) quantum shell: the 2s, 2p_x, 2p_y, and 2p_z In an isolated carbon atom there is a full 2s orbital and two half-filled p orbitals. When the carbon atoms form a bond, these orbitals are somehow mysteriously transformed into four new bonding orbitals, which are called sp³ hybrid orbitals because they are a mixture of an s and three p orbitals. These sp³ orbitals exist only in the context of bonded carbon; they are not present in isolated carbon atoms. They spring into existence when one carbon atom interacts with another atom to form a bond; they are generated through the interaction. In the case of carbon the four electron clouds (bonds) move as far apart as possible to minimize the repulsions between them, adopting a tetrahedral configuration.

The Molecular Orbital Model

Another way to consider how these bonds form is similar to the way we approached molecular hydrogen. That is, we consider that when carbon–carbon (C–C) bonds form, atomic orbitals are transformed into molecular orbitals (MOs). For each stabilizing bonding orbital, a destabilizing antibonding orbital is also formed. Using the molecular orbital approach, we can model the bonding in diamond as carbon atoms forming a three-dimensional network held together by these molecular bonding orbitals. C–C bonds are very stable because there is a large energy gap between the bonding orbitals and the high-energy antibonding orbitals. The bonding molecular orbitals are occupied while the antibonding molecular orbitals are unoccupied. Because of this large gap between the filled bonding and empty antibonding orbitals it is hard to remove an electron from a C–C bonding MO. The electrons are not free to move between energy levels. Given that electrical conduction depends upon the relatively free movement of electrons it is not surprising that diamonds do not conduct electricity. But why, you might ask, is a diamond transparent, rather than opaque, like a block of graphite, which is also composed of only carbon atoms? For an object to be transparent most of the light that hits it must pass through it; the light can be neither reflected or absorbed. For a diamond to absorb light a photon would need to move an electron from a low-energy bonding MO to a high-energy antibonding orbital. However, visible light does not have enough energy to bridge the energy gap between the bonding and antibonding orbitals. Based on this thinking we conclude that there is something different between bonds holding C atoms together in diamond from the bonds holding C atoms together in graphite even though we do not know, at this point, what it could be.

An important point to consider here is that we have described the bonding in carbon using two different models: the hybrid orbital (valence bond) and molecular orbital models. Although this may be (a bit!) confusing, and may take some getting used to, it is quite common to describe chemical and physical phenomena using different models. Typically we use the simplest model that will allow us to explain and predict the phenomenon we are interested in. Usually the bonding in carbon is described using the hybrid orbital model, because it is highly predictive and easier to use in practice.

Graphite

As we have already mentioned, different allotropes (different forms of the same element) can have quite different properties. The carbon allotrope graphite is soft, grey/black, opaque, conducts electricity, and slippery – it makes a good lubricant.^[3] Diamond is hard, transparent, and does not conduct electricity. How can this be possible if both are pure carbon? The answer lies in how the carbon atoms are organized with respect to one another. Whereas the carbon atoms in diamond form a three-dimensional network, in graphite, the atoms are organized in two-dimensional sheets that stack one on top of the other. Within each two-dimensional sheet the carbon atoms are linked by covalent bonds in an extended array of six-membered rings. This means that the carbon sheets are very strongly bonded, but the interactions between sheets are much weaker. Although there are no covalent bonds between the sheets, the atoms of the sheets do interact through London dispersion forces, very much like the interactions that hold helium atoms together. Because the sheets interact over very much larger surface areas, however, these interactions are much stronger than those in helium. Yet another allotrope of carbon, graphene, consists of a single sheet of carbon atoms.^[4] These sheets can be rolled into tubes to form nanotubes that are the subject of intense research interest because of their inherently high tensile strength. Carbon atoms can also form spherical molecules, known as buckminsterfullerenes or buckyballs.^[5]

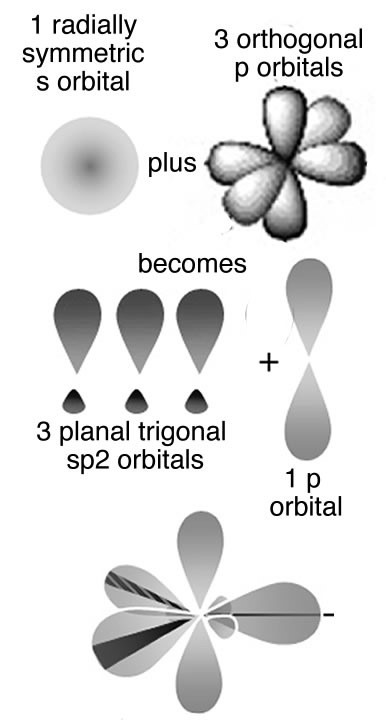
The obvious question is, why don’t covalent bonds form between graphite sheets? Why are the patterns of covalent bonding so different: three-dimensional (tetrahedral) in diamond, with each carbon bonded to four others, and two-dimensional (planar) in graphite and graphene, with each carbon atom bonded to only three others? One way to describe the molecular structure is to use the hybrid orbital bonding model. As we discussed previously, to form the four bonds attached to each carbon atom in diamond, we needed to hybridize four atomic orbitals to form four bonding orbitals. We might think we only need three bonds in graphite/graphene because each carbon is only connected to three others. This is not exactly true. In graphite and graphene we use a model in which only three atomic orbitals are hybridized—an s and two 2p orbitals in order to form three sp² bonding orbitals. These orbitals attach each carbon atom to three other atoms. Just like in diamond the three bonds associated with each carbon atom in graphite/graphene move as far apart as possible to minimize electron pair repulsion; they lie at the points of a triangle (rather than a tetrahedron). This geometry is called trigonal planar and the C–C–C bond angle is 120°.

All well and good, but this does not really explain why the carbons in graphite/graphene are attached to three other carbon atoms, whereas in diamond each carbon is attached to four others. Perhaps surprisingly there is no good answer for why carbon takes up different forms—except that it can. But in fact carbon does form four bonds in graphite (carbon almost always forms four bonds—a central principle of organic chemistry). The trick is that the four bonds are not always equivalent; in graphite the fourth bond is not formed by the sp² bonding orbitals but rather involves an unhybridized 2p atomic orbital. These p orbitals stick out at right angles to the sheet and can overlap with p orbitals from adjacent carbons in the same sheet (see Figure). Remember that p orbitals have two regions of electron density. To explain the fact that graphite conducts electricity, we use an idea from molecular orbital (MO) theory, namely that bonding and antibonding MOs are formed from the adjacent p orbitals that extend over the sheet surface. The energy different between these orbitals is not large and electrons can move from one to the other, allowing the movement of electrons throughout the whole sheet of graphite, which gives it many of the properties that we associate with metals. Note that we use both the hybridization model, which explains the planar framework of C–C bonds in graphite, and molecular orbital theory, which explains graphite’s electrical conductivity. So before we delve further into the properties associated with graphite, let us take a look at bonding in metals.

Up until this point we have considered only bonds between atoms of the same element. While this makes things simpler (although you might not agree after thinking about the many forms of carbon), it leaves out the vast majority of the compounds that exist in the world and their chemistries. Moreover, pure elements are rare in nature. Much of the efforts of alchemists, early chemists, and the modern refining industry involve determining how to (economically) separate specific types of atoms (elements) away from others. Modern chemistry is concerned (largely) with putting atoms together to form new and useful molecules. Both involve understanding the concepts underlying how atoms interact.

3D and 2D Representations

To extend our discussion to the wider world of what we might call heterogenous molecules, that is, molecules made up of atoms of more than one element, we will begin with carbon. Why carbon? Well, here are some reasons. Carbon is the fourth most abundant element in the universe (~3,032 atoms per million), after hydrogen (~705,700 atoms per million), helium (~275,200 atoms per million), and oxygen (~5,920 atoms per million). Carbon is distinguished from most other elements in its ability to form a vast array of diverse compounds by bonding with itself and other elements with bonds that are not too strong and not too weak. Under the conditions that persist on the surface of the Earth carbon compounds are stable enough to hang around but not stable enough to persist forever, so they are not dead ends. Carbon is a key building block of the major molecules of life: proteins, nucleic acids, lipids, and carbohydrates. We are carbon-based life forms! Carbon compounds are also used in a wide range of synthetic materials, such as pharmaceuticals, polymers, and high-tech materials; we also consume a lot of carbon compounds by burning them for fuel.

Carbon: Always Tetravalent and Often Tetrahedral

Atoms combine in many different ways. We have already seen an example of how a covalent bond can form between two hydrogen atoms producing molecular (H₂) as opposed to the atomic form of hydrogen. Similarly atoms of carbon can be linked together in various ways to form diamond, graphite, and graphene. Now we move on to molecules involving atoms of carbon and other elements. In keeping with our ongoing attempt to keep things simple (or better put, as simple as possible), let us start by examining the types of molecules that can be formed by combining carbon with hydrogen. There are many such molecules, and collectively they are known as hydrocarbons. The simplest such compound is methane CH₄, a major component of natural gas. As in all its compounds and its elemental forms, carbon is tetravalent, which means that it always forms four bonds. We will now consider in greater detail why this is so, what forms the bonds can take, and what are the consequences of this fact. In this discussion, we will be building on the ideas introduced when we talked about diamond, graphite, and graphene.

To answer these questions we need to return to the ideas about the quantization of electron energy levels. Carbon has a total of six electrons, two of which are in a filled (1s) quantum shell, and four valence electrons; it is these valence electrons that can take part in bonding. Remember that the formation of a bond always lowers the energy of a system. It therefore makes sense that a carbon atom would form as many bonds as possible, resulting in the most stable possible molecular species.

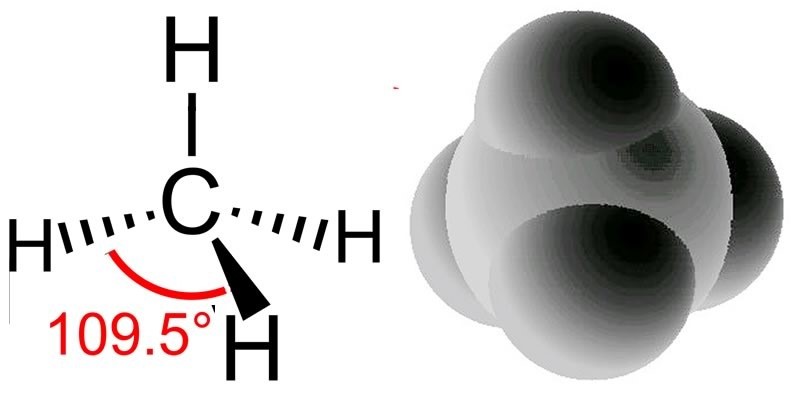
What happens if we combine hydrogen with carbon? Do we get a compound with properties intermediate between the two? Absolutely not, as you might have expected when considering the differences between diamonds and graphite. As previously we use the hybridization model to explain the behaviors we observe. We begin with what we know: in methane the carbon atoms make four bonds, one to each of four hydrogen atoms. We also know, from experiment, that the shape of the methane molecule is tetrahedral; there is a carbon at the center and the four C–H bonds pointing towards the corners of a four-sided figure. Since each C-H bond is formed from bonding orbitals we can use the model for bonding where these four bonding orbitals arise from the “hybridization” of the pre-existing 2s and three 2p atomic orbitals. The electrons in the 1s orbital are not used because the amount of energy needed to use those electrons is greater than the energy that would be released upon bond formation (they are held tightly to the nucleus by the electromagnetic force). It turns out to be a general rule that electrons in the core of the atom—in filled shells—tend not to take part in bonding. This means we need only consider the valence electrons when thinking about bonding.

The hybridization of the 2s and the three 2p orbitals results in four sp3 molecular orbitals, each of which can interact with the H atom’s 1s orbital to form a bond. When a bonding orbital is formed it contains two electrons. Because carbon has four valence electrons and each of the four hydrogens has one electron the result is a total of eight electrons distributed in four bonding orbitals.

Recall that we say the hybridization of carbon is sp3 and the arrangement of the bonds is tetrahedral, which means the angle between orbitals (and the C–H bonds) is 109.5º. Another way to say this is that the H–C–H bond angle is 109.5º. We can predict that this will be the case based on theoretical calculations; these have been confirmed by experimental observations. But why should this be true? How many different arrangements are there for four hydrogens bonded to a single carbon? Why aren’t the hydrogens all arranged in a single plane (around a central C with 90º bond angles) rather than in the tetrahedral arrangement? The planar arrangement, which is known as a square planar geometry, is actually possible and is sometimes observed under some special conditions, usually in molecules involving transition metals as we will see later). The square planar arrangement is not as stable as the tetrahedral arrangement for carbon because each C–H bond can be considered as a region of high electron (negative charge) density. Given that like repels like, each bond repels the others and moves as far away from the other bonds as possible. The optimum bond angle turns out to be 109.5º away from each of their neighbors. At that point, if they moved away from one orbital they would move closer to another. You may want to convince yourself of this geometric fact by using a marshmallow, toothpicks, and gumdrops! This principle goes by the unwieldy name of valence shell electron pair repulsion (VSEPR) and can be used to predict (once you get the hang of it) the three-dimensional (3D) structure of simple molecules—assuming that you know how the atoms within a molecule are connected. For example, using VSEPR logic, you should be able to present a compelling argument for why the C–H bonds in methane do not adopt a square planar orientation, as well as the general shape of many other types of molecules. You can even go further, in methane all four atoms attached to the central carbon are the same but what if they are different? You should be able to make plausible predictions about how bond angles would change if one of the attached groups is larger than the others – how would that influence bond angles?

One problem for many people is that 3D visualization of molecular structures is not easy. It is particularly tricky when one is called upon to translate the more or less abstract two-dimensional (2D) representations (Lewis and dot stuctures ↓) that you find printed on the page of a book, into a 3D model you can manipulate with your hands or in your mind. In addition, chemists (and molecular biologists) have an annoying tendency of representing complex 3D structures using various 2D representations, which can be confusing if you don’t know what you are looking at (or for). You have probably already seen some of these different structures, and we will consider a number of them below. Each provides specific kinds of information about the molecule. Note that actual 3D physical models and web activities can be very helpful in solidifying your ideas about structure.

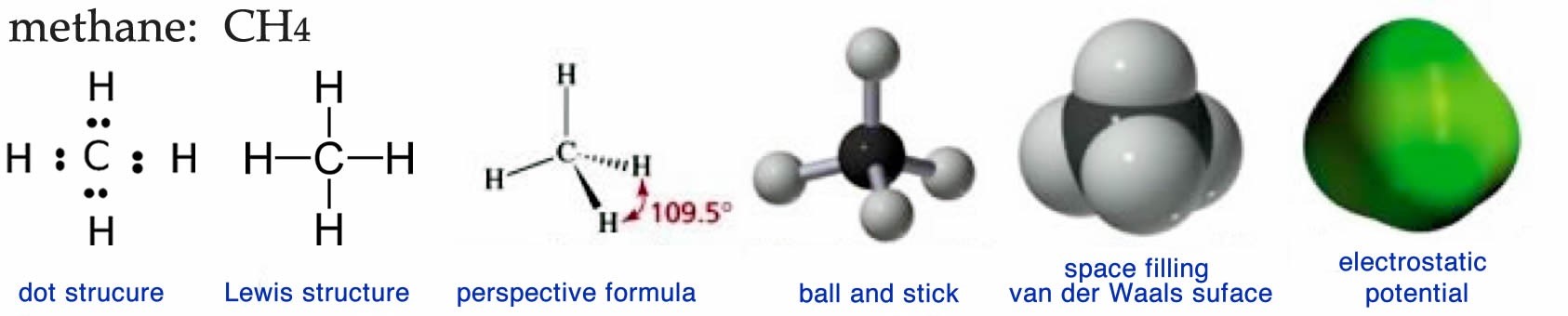
If we were able to see a methane molecule, what we observe would probably be closest to the electrostatic potential map. This visualization provides a picture of the surface of the molecule, generally color coded to represent fluctuations in electron density. Notice that there are no color fluctuations on this model of methane indicating that there are no (permanent) electron cloud distortions in the molecule—the surface of the molecule is uniformly electrically neutral. What is not so easy to discern from this representation is the fact that the methane is tetrahedral or that the central carbon atom is bonded to four hydrogen atoms, a fact that is much easier to appreciate in the other representations. The electrostatic potential representation is very useful for large biological molecules for several reasons: it is much simpler than the other kinds of models because individual atoms are not represented; it shows the molecule’s shape; and it shows where charges and partial charges are located.

The space-filling or van der Waals model gives more structural information in that the individual atoms that make up the molecule are distinguished by color (black for carbon, white for hydrogen, red for oxygen, and blue for nitrogen.) The surface of the model represents the molecule’s van der Waals radius, which is the distance where attraction turns to repulsion when two molecules approach one another. As its name implies, such models represent the space occupied by each atom.

The ball-and-stick model of methane shows the central carbon (black ball) attached to four hydrogens (white balls) by sticks that represent the bonds between the atoms. Although this model is probably the easiest to visualize, it is misleading because it could give the impression that bonds are like sticks holding the atoms together. It also does not represent either the actual volume occupied by the molecule or its electrostatic surface features. Another problem with all three of the preceding types of models is that you need a computer and specialized software (or some artistic ability) to draw them, which may not always be convenient or possible.

One strategy to address this problem is through what is known as a perspective formula. In a perspective formula the atoms are represented by their atomic symbols (for example, C or H) and bonds are represented by various kinds of lines. A normal line is meant to indicate a bond that is in the plane of the paper, a wedged line  represents a bond that is coming out of the plane toward you (the reader), and a hatched line  represents a bond that is coming out of the plane, but away from you. This convention makes it easier to draw 3D perspective structures by hand without specialized software (or graphical talent.) We can, in fact, go one step further and draw methane without indicating its 3D structure at all. Structures that show all the bonds, atoms, and any valence electrons that are not in bonds, but do not attempt to accurately represent the 3D shape of a molecule are called Lewis structures. The Lewis structure for methane (see above) and the molecular formula CH₄ represent a chemical shorthand that can provide a huge amount of information; we will see even more extreme examples as we go on. However, to be able to understand these representations, you must already know that the methane molecule is tetrahedral and the rules that apply to the geometry of carbon bonds, because neither is shown explicitly. If you didn’t know these things, you might even be tempted to assume that methane is organized with a square planar geometry or that the hydrogens are all located to one side of the carbon atom, neither of which is true!

Why, you might ask, would one want to draw structures with so much information missing?  Perhaps, like medieval alchemists, modern chemists want to keep their secrets from the average person. Perhaps they just like secret codes and mystical symbols. Or perhaps it is because these shorthand representations of molecules are just much more compact and easy to draw, particularly when we get to large molecules with lots of atoms.^[6]  Drawing Lewis structures is an important and useful chemistry skill and we will return to it in more detail shortly. Once you have mastered it you will be able to look at a molecular formula such as CH₄ (or C₅H₁₂) and (together with other information) be able to visualize the 3D structure of the molecule represented and predict many of the substance’s physical and chemical properties.

For example, models of the methane molecule predict that it is symmetrical. Again, this might not be entirely obvious just by looking at the structure, but if you make a model, or look at a rotatable interactive 3D model on the web you will see that it does not matter which way you look at the structure—all the C–H bonds are the same, and all the bond angles are the same. A little more information (which we will discuss later on) will let you deduce that there are no permanent electron density distortions in the molecule—just as is shown by the electrostatic potential map. Together these enable you to deduce that methane molecules are attracted to one another solely through London dispersion forces (like helium atoms or hydrogen molecules). Given how weak these interactions between molecules are we might be brave enough to predict that the melting and boiling points of methane are low (melting and boiling occur at relatively low temperatures) and we would be right! Methane melts at 91 K and boils at 112 K.^[7]

Building Increasingly Complex Molecules

You will soon realize that it is possible to build a rather amazing number of compounds using just hydrogen and carbon. For example imagine that we remove one hydrogen from a methane molecule; this leaves us with what is known as a methyl (-CH₃) group. We can combine two methyl groups by forming a C–C bond between them (you might want to convince yourself that each carbon atom is still making four bonds with neighboring atoms). The resulting molecule is known as ethane (→). The structure of ethane can be written in a number of ways, for example H₃C-CH₃, CH₃ –CH₃ or C₂H₆. As the number of atoms increases so does the number of different ways a molecule can be represented. It is for this reason that chemists have developed a number of rules that are rather strictly adhered to; these rules make it possible to unambiguously communicate the structure of a molecule to others.^[8] We will not spend much time on all of these various rules but there are web activities that you can do if you want to get an introduction and to practice them. These naming conventions are controlled by the International Union of Pure and Applied Chemistry, known as IUPAC and these rules can be found in the Compendium of Chemical Terminology.^[9]

The process of removing hydrogens and adding methyl groups can continue, essentially without limit, to generate a family of hydrocarbons^[10] known as the alkanes; the rules that govern these molecules are simple: each hydrogen makes one and only one bond; each carbon must make four discrete bonds; and these four bonds are tetrahedral in orientation. The number of carbons is in theory unlimited and how they are linked together determines the number of hydrogens. (Can you see how two hydrocarbons with the same number of carbon atoms could have different numbers of hydrogens?)

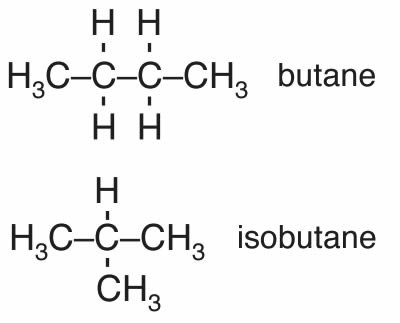Depending on how the carbons are connected it is possible to generate a wide variety of molecules with dramatically different shapes. For example there are cage-like, spherical, and long, string-like alkanes. Consider the four-carbon alkanes. There are butane and isobutane that have the formula C₄H₁₀ as well as others with four carbons but different numbers of hydrogens, for example: cyclobutane, methylcyclopropane, and tetrahedrane. Butane has a boiling point of -0.5ºC, and isobutane has a boiling point of -11.7ºC. Why are the boiling points of butane and isobutane, which have the same atomic composition (C₄H₁₀), different? The answer lies in the fact that they have different shapes. The roughly linear carbon chain of butane has a larger surface area than isobutane, which gives it more surface area through which to interact with other molecules via London dispersion forces. This idea, that the shape of a molecule and its composition, determine the compound’s macroscopic properties is one that we will return to repeatedly.

Single Bonds and Molecular Shape

C–C and C–H bonds are described by molecular orbitals; calculations indicate that most of the electron density associated with these orbitals lies between the two nuclei. The C–H bonds have a length of 109 × 10^-12 m (109 pm) while the C–C bond is approximately 50% longer, 154 × 10^-12 m (154 pm). This is because the C–C bonding orbital is made from sp³ hybrid orbitals, which are larger than the 1s orbital that hydrogen uses to form bonds. These so-called σ (sigma) bonds have an interesting property; the atoms that they link can spin relative to each other without breaking the bond between them. For a C–H bond, if the H spins it would be impossible to tell, since the H atom is radially symmetric around the C–H bond axis. But if the carbons in the C–C bond of ethane spin relative to each other, then it is possible to observe different arrangements by looking down the C–C bond axis.

For example: 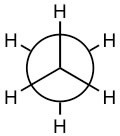and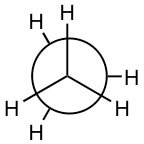 are both representations of ethane (the C–C bond is not seen in this depiction because you are looking straight down the C–C bond). They appear different because the arrangement of the atoms is different in space, but in fact at room temperature these two arrangements can easily interconvert by rotating around the C–C bond.

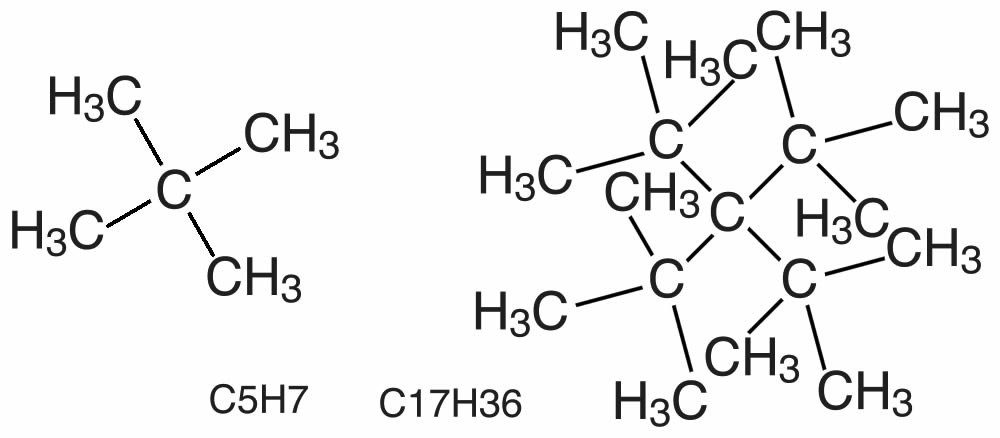
This raises another point to consider, namely that starting (and stopping) bond rotations requires energy. Similarly, there can be vibrations along the length of a bond, which again involves the absorption or release of energy. We will consider this further later on.^[11] In the case of the rotating bond it turns out that as the bulk of the groups attached to the carbons increases the energy required for the rotation around the C–C bond also increases. Big, bulky groups can bump into each other, occupying each other’s space causing electron-electron repulsions and raising the energy of any shape where the groups are too close. This tends to lock the molecule into specific orientations that can influence the compound’s physical properties. An example of how structure interferes with the formation of a molecule is a molecule containing 17 carbon atoms and 36 hydrogen atoms; although it is possible to draw this molecule it has never been synthesized because the atoms crowd each other, and intrude on each other’s space. It is possible, however, to synthesize molecules with the same number of carbon atoms but fewer hydrogen atoms.^[12] Can you produce a plausible explanation for why?

Collapsing Real Structures Down to 2-Dimensional Representations

Now, an obvious problem with complex three-dimensional molecules, even those made up only of hydrogen and carbon, is how to convey their structure when they must be depicted in two dimensions, like when you are writing on paper. Research indicates that students (that is, most people) have a tough time with this task, which is why we will describe various approaches here.

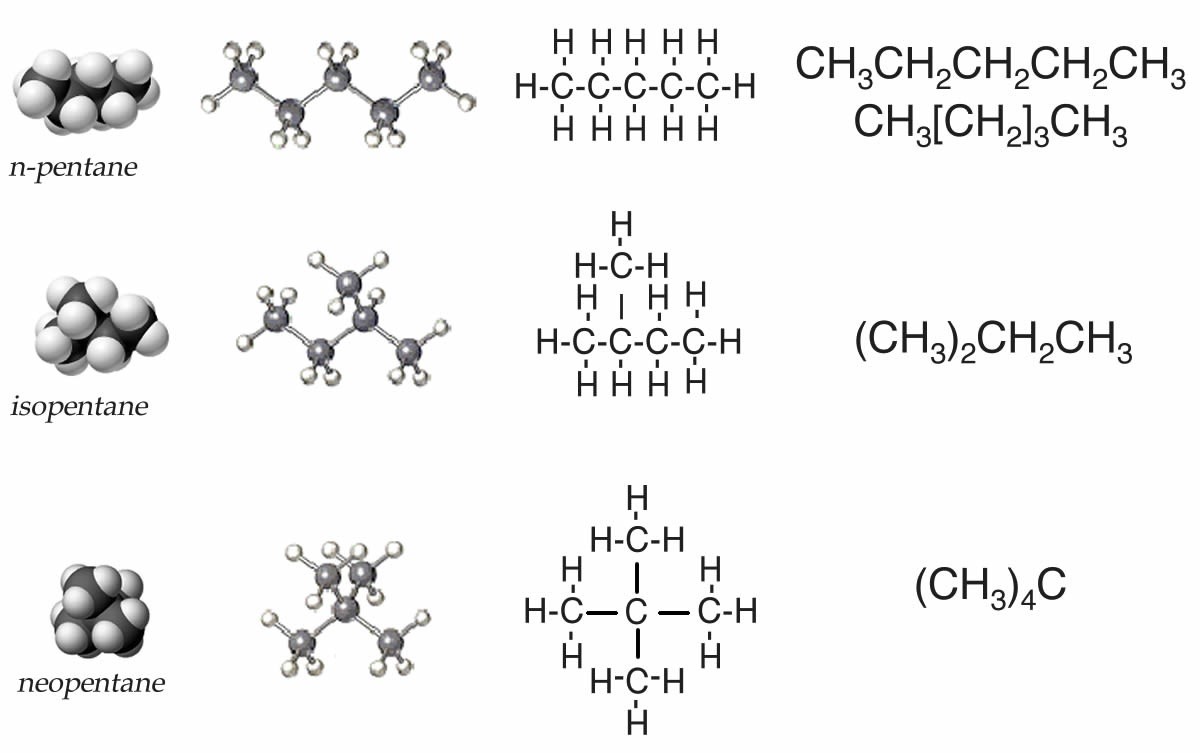Before we begin, we need to have some rules. Let us use the set of possible molecules that contain 5 carbon atoms and 12 hydrogen atoms; these are generically known as pentanes. You can begin with a piece of paper and a pencil; how many different molecules can you draw with the composition of C₅H₁₂? Clearly C₅H₁₂ does not uniquely define the structure of the molecule; it is better to use their distinct names: pentane, isopentane, and neopentane. Each of the different molecules you have drawn has the same molecular formula but a different shape and, it turns out, different properties. For example, pentane has a boiling point of 308 K, whereas the boiling points of isopentane and neopentane are 301 K and 283 K, respectively. Their shape, rather than their elemental composition, influences the strength of the attractions between the individual molecules, which in turn influences their boiling points. We call these kinds of related compounds structural isomers, which means they have the same composition (for example C₅H₁₂) but their constituent atoms are connected differently to give different structures and shapes.

It is common to use a number of different types of representations to picture molecules. One way is through what are known as text formulas (or linear formulae). In this scheme, pentane is written CH₃–CH₂–CH₂–CH₂–CH₃, which can also be written as CH₃–[CH₂]₃–CH₃. This captures some of the structural subtleties of pentane, but not all. For example, it does not illustrate the fact that the molecule is not strictly linear. Nevertheless, we can already anticipate complications. How would we write isopentane? The most obvious way would be (CH₃)₂CHCH₂CH₃. Neopentane is written as (CH₃)₄C. Does that make sense? Try deciphering them.

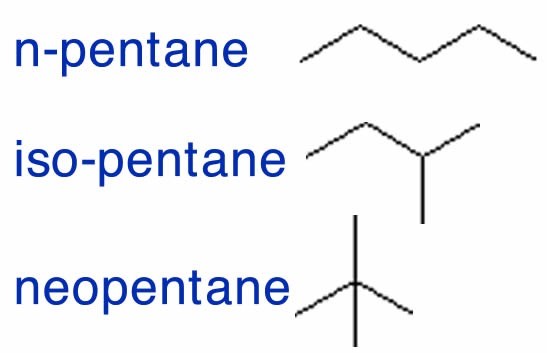If we followed the logic of this approach we could draw a more complete representation of pentane, isopentane, and neopentane as Lewis structures, but again, we are missing the three-dimensionality. You might even be led to think that the molecules are actually flat when they are much more like balls. Although it is possible to make the representation a little more realistic by trying to indicate three-dimensionality using the wedge and dash symbols, these structures become very complicated very fast. It is not really practical to draw out full 3D structures for larger, complex molecules. One important skill you will need to master is the ways that short-hand structures (such as Lewis structures) can provide information about the 3D structure of a molecule that allows us to predict chemical and physical properties.

There is one more representation you will often see used that leaves out even more information. In the line structure the only things that are shown are the bonds between carbons! So for example for the pentanes (C₅H₁₂) we can draw structures such as those shown in the figure that omit all the symbols for atoms and all the C–H bonds. These structures should be used with caution because it is very easy to forget atoms or bonds when they are not in the representation. But what these line structures do show clearly is how the carbon atoms are connected, which can be very helpful at times.

Double and Triple Bonds

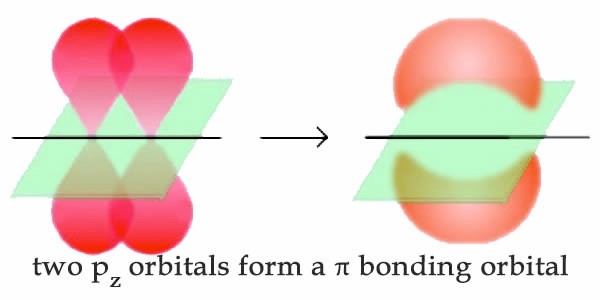So far, we have considered what are known as single bonds; that is, all the C–C and C–H bonds in alkanes, and all the bonds in diamond. Each single bond involves two (and only two) electrons that are described by a bonding molecular orbital. In such a bonding orbital, most of the electron density is located between the two bonded atoms in a linear sigma (σ) bond. We have, however, already discussed albeit briefly bonds that involve more than one pair of electrons, namely those found in graphite. Recall that for graphite and graphene the bonds between carbon atoms in the sheet plane involve hybridized orbitals that are mixtures of the 2s²  and 2p_x and 2p_y (that is sp² hybrid orbitals) leaving an unhybridized 2p_z  orbital. On bonding, these unhybridized 2p_z orbitals reorganize to form what is known as a pi (π) bonding orbital. In π orbitals, the electron density lies above and below the axis connecting the bonded atoms. The combination of σ and π bonding orbitals produces a double bond. Double bonds are indicated by two lines, for example as in CH₂=CH₂ (ethene).

Shapes of Molecules with Double (and Triple) Bonds

We can apply the same thinking about the arrangement of bonds around the carbon atoms in CH₂=CH₂ in much the same manner as we did for CH₃-CH₃. In ethene each carbon atom is surrounded by three centers of electron density, two Hs and one C. Note that the double bond counts as a single center of electron density. There are a number of important points to keep in mind when considering the effects of double bonds on a molecule and its properties. First, a C=C double bond is typically less stable (that is more reactive) than two separate single bonds. When we come to thinking about reactions we will find that replacing a double bond by two single bonds typically produces a more stable system. Second, although there is more or less free rotation around the axis of a single bond at room temperature, rotation is blocked by the presence of a double bond. For a rotation to occur, the π bond (in which there is electron density above and below the axis between the two carbon atoms) must be broken and then reformed. The presence of a double bond has distinct effects on molecular shape. The minimum energy arrangement for three centers is a two-dimensional arrangement in which the groups are oriented at about 120º to one another; an arrangement known as trigonal planar geometry.

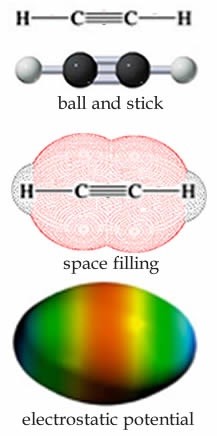There is one more common type of bond that carbon can form, which is a triple bond. For example each carbon in C₂H₂ (ethyne) is surrounded by only two centers of electron density: a single sp hybrid orbital bonds between a carbon atom and a hydrogen atom and a triple bond, which can be thought of as a σ bond and two π bonds between the carbons, shown in the figure. The lowest energy arrangement around each carbon is a line in which the angle between the bonds is 180º. As before, a triple bond is less stable than three single bonds, and reactions can be expected!

We see that under most conditions, a carbon atom can participate in a maximum of four bonds; either four single bonds, two single bonds and a double bond, or one single bond and a triple bond.