"

Entropy

Dispersal of Matter and Energy

As we extend our discussion of thermodynamic concepts toward the objective of predicting spontaneity, consider now an isolated system consisting of two flasks connected with a closed valve. Initially there is an ideal gas on the left and a vacuum on the right (Figure 1). When the valve is opened, the gas spontaneously expands to fill both flasks. Since the system is isolated, no heat has been exchanged with the surroundings (q = 0). The first law of thermodynamics confirms that there has been no change in the system’s internal energy as a result of this process.

A diagram shows two two-sided flasks connected by a right-facing arrow labeled “Spontaneous” and a left-facing arrow labeled “Nonspontaneous.” Each pair of flasks are connected to one another by a tube with a stopcock. In the left pair of flasks, the left flask contains thirty particles evenly dispersed while the right flask contains nothing and the stopcock is closed. The right pair of flasks has an open stopcock and equal numbers of particles in both flasks.
Figure 1. An isolated system consists of an ideal gas in one flask that is connected by a closed valve to a second flask containing a vacuum. Once the valve is opened, the gas spontaneously becomes evenly distributed between the flasks.

The spontaneity of this process is therefore not a consequence of any change in energy that accompanies the process. Instead, the driving force appears to be related to the greater, more uniform dispersal of matter that results when the gas is allowed to expand. Initially, the system was comprised of one flask containing matter and another flask containing nothing. After the spontaneous process takes place, the matter distributes both more widely (occupying twice its original volume) and more uniformly (present in equal amounts in each flask).

Now consider two objects at different temperatures: object X at temperature TX and object Y at temperature TY, with TX > TY (Figure 2). When these objects come into contact, heat spontaneously flows from the hotter object (X) to the colder one (Y). This corresponds to a loss of thermal energy by X and a gain of thermal energy by Y. From the perspective of this two-object system, there was no net gain or loss of thermal energy; rather, the available thermal energy was redistributed between the two objects. This spontaneous process resulted in a more uniform dispersal of energy.

Two diagrams are shown. The left diagram is comprised of two separated squares; the left is red and labeled “X” and the right is blue and labeled “Y.” Below this diagram is the label “T subscript X, a greater than sign, T subscript Y.” The right diagram shows the boxes next to one another, shaded red on the left, blue on the right, and blended red and blue together in the middle. The left box is red and labeled “X,” the right is blue and labeled “Y” and a right-facing arrow labeled “Heat” is written above them. Below this diagram is the label “X and Y in contact.
Figure 2. When two objects at different temperatures come in contact, heat spontaneously flows from the hotter to the colder object.

As illustrated by the two processes described, an important factor in determining the spontaneity of a process is the extent to which it changes the dispersal or distribution of matter and/or energy. In each case, a spontaneous process took place that resulted in a more uniform distribution of matter or energy.

Example 1

Describe how matter is redistributed when the following spontaneous processes take place:

  1. A solid sublimes.
  2. A gas condenses.
  3. A drop of food coloring added to a glass of water forms a solution with uniform color.

Solution

(a) Sublimation is the conversion of a solid (relatively high density) to a gas (much lesser density). This process yields a much greater dispersal of matter, since the molecules will occupy a much greater volume after the solid-to-gas transition.

(b) Condensation is the conversion of a gas (relatively low density) to a liquid (much greater density). This process yields a much lesser dispersal of matter, since the molecules will occupy a much lesser volume after the solid-to-gas transition.

(c) The process in question is dilution. The food dye molecules initially occupy a much smaller volume (the drop of dye solution) than they occupy once the process is complete (in the full glass of water). The process therefore entails a greater dispersal of matter. The process may also yield a more uniform dispersal of matter, since the initial state of the system involves two regions of different dye concentrations (high in the drop, zero in the water), and the final state of the system contains a single dye concentration throughout.

Check Your Learning

Describe how matter and/or energy is redistributed when you empty a canister of compressed air into a room.

Answer

This is also a dilution process, analogous to example (c). It entails both a greater and more uniform dispersal of matter as the compressed air in the canister is permitted to expand into the lower-pressure air of the room.

Predicting the Sign of ΔS

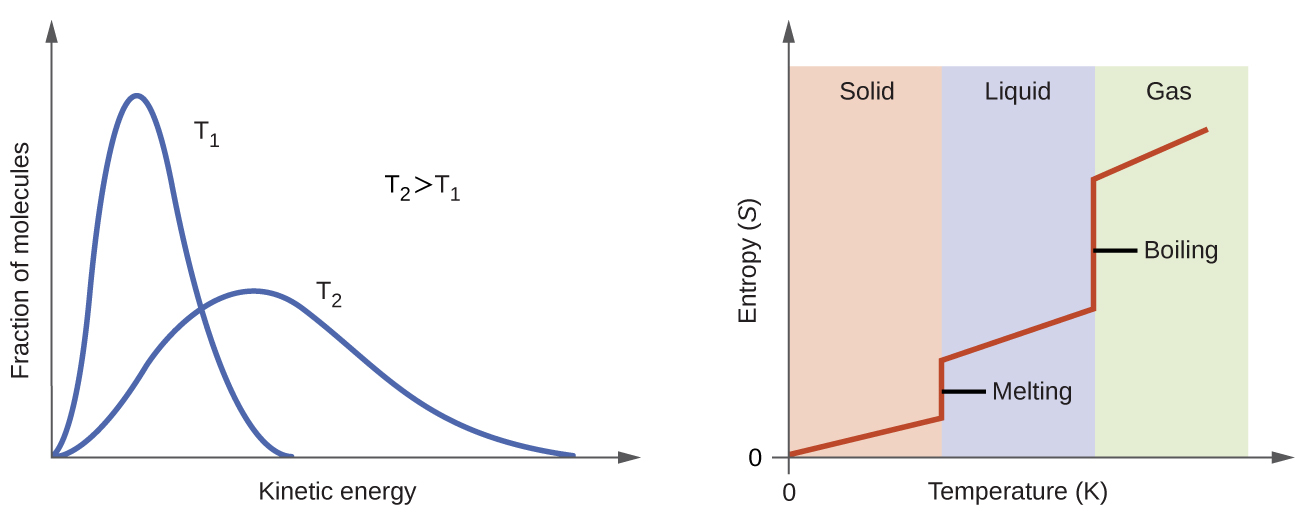
The relationships between entropy, microstates, and matter/energy dispersal described previously allow us to make generalizations regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes. Consider the phase changes illustrated in Figure 3. In the solid phase, the atoms or molecules are restricted to nearly fixed positions with respect to each other and are capable of only modest oscillations about these positions. With essentially fixed locations for the system’s component particles, the number of microstates is relatively small. In the liquid phase, the atoms or molecules are free to move over and around each other, though they remain in relatively close proximity to one another. This increased freedom of motion results in a greater variation in possible particle locations, so the number of microstates is correspondingly greater than for the solid. As a result, Sliquid > Ssolid and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, ΔS > 0. By the same logic, the reciprocal process (freezing) exhibits a decrease in entropy, ΔS < 0.

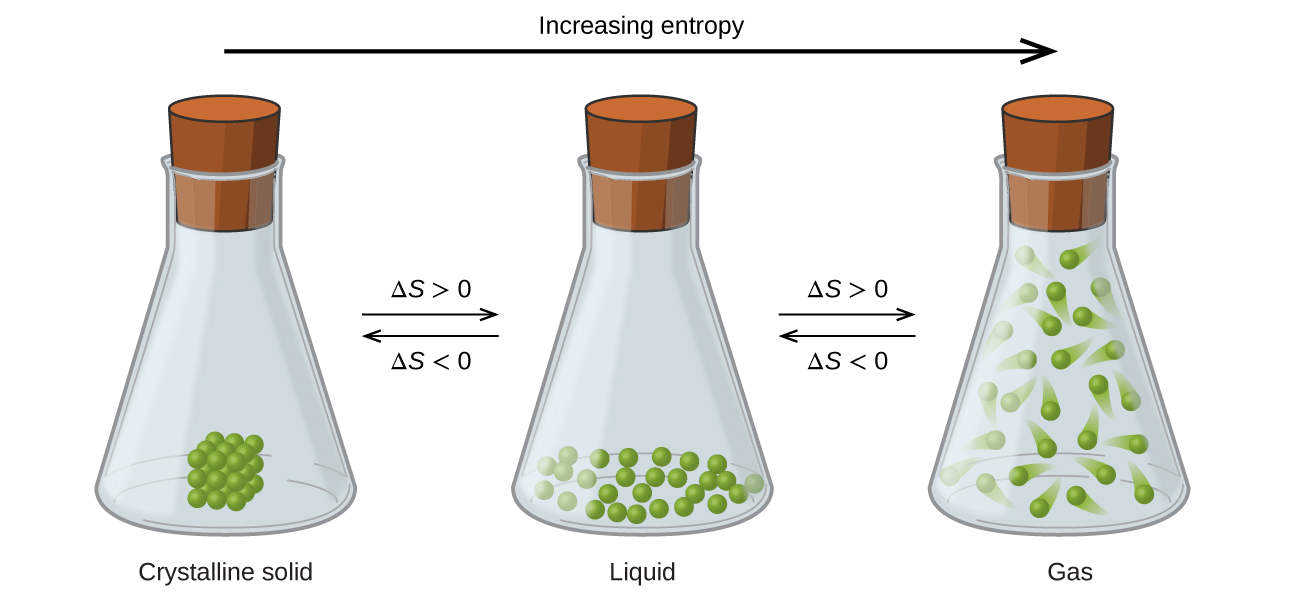
Three stoppered flasks are shown with right and left-facing arrows in between each; the first is labeled above as, “delta S greater than 0,” and below as, “delta S less than 0,” while the second is labeled above as, “delta S greater than 0,” and below as, “delta S less than 0.” A long, right-facing arrow is drawn above all the flasks and labeled, “Increasing entropy.” The left flask contains twenty-seven particles arranged in a cube in the bottom of the flask and is labeled, “Crystalline solid,” below. The middle flask contains twenty-seven particles dispersed randomly in the bottom of the flask and is labeled, “Liquid,” below. The right flask contains twenty-seven particles dispersed inside of the flask and moving rapidly and is labeled, “Gas,” below.
Figure 3. The entropy of a substance increases (ΔS > 0) as it transforms from a relatively ordered solid, to a less-ordered liquid, and then to a still less-ordered gas. The entropy decreases (ΔS < 0) as the substance transforms from a gas to a liquid and then to a solid.

Now consider the vapor or gas phase. The atoms or molecules occupy a much greater volume than in the liquid phase; therefore each atom or molecule can be found in many more locations than in the liquid (or solid) phase. Consequently, for any substance, Sgas > Sliquid > Ssolid, and the processes of vaporization and sublimation likewise involve increases in entropy, ΔS > 0. Likewise, the reciprocal phase transitions, condensation and deposition, involve decreases in entropy, ΔS < 0.

According to kinetic-molecular theory, the temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature of a substance will result in more extensive vibrations of the particles in solids and more rapid translations of the particles in liquids and gases. At higher temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also broader (more dispersed) than at lower temperatures. Thus, the entropy for any substance increases with temperature (Figure 4).

Two graphs are shown. The y-axis of the left graph is labeled, “Fraction of molecules,” while the x-axis is labeled, “Velocity, v ( m / s ),” and has values of 0 through 1,500 along the axis with increments of 500. Four lines are plotted on this graph. The first, labeled, “100 K,” peaks around 200 m / s while the second, labeled, “200 K,” peaks near 300 m / s and is slightly lower on the y-axis than the first. The third line, labeled, “500 K,” peaks around 550 m / s and is lower than the first two on the y-axis. The fourth line, labeled, “1000 K,” peaks around 750 m / s and is the lowest of the four on the y-axis. Each line get increasingly broad. The second graph has a y-axis labeled, “Entropy, S,” with an upward-facing arrow and an x-axis labeled, “Temperature ( K ),” and a right-facing arrow. The graph has three equally spaced columns in the background, labeled, “Solid,” “Liquid,” and, “Gas,” from left to right. A line extends slightly upward through the first column in a slight upward direction, then goes straight up in the transition between the first two columns. In then progresses in a slight upward direction through the second column, then goes up dramatically between the second and third columns, then continues in a slight upward direction once more. The first vertical region of this line is labeled, “Melting,” and the second is labeled, “Boiling.”
Figure 4. Entropy increases as the temperature of a substance is raised, which corresponds to the greater spread of kinetic energies. When a substance melts or vaporizes, it experiences a significant increase in entropy.

The entropy of a substance is also influenced by structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relationship between a particle’s mass and the spacing of quantized translational energy levels (which is a topic beyond the scope of this course). For molecules, greater numbers of atoms (regardless of their masses) increase the ways in which the molecules can vibrate and thus the number of possible microstates and the system entropy.

Finally, variations in the types of particles affects the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system comprised of nonidentical components. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increase in entropy, ΔS > 0.

Summary of Entropy
  • Sgas > Sliquid > Ssolid
  • The entropy for any substance increases with temperature.
  • Heavier atoms possess greater entropy at a given temperature than lighter atoms.
  • For molecules, greater numbers of atoms in a molecule increase the system entropy.
  • The entropy of a mixture of two or more different particle types is greater than that of a pure substance.

Considering the various factors that affect entropy allows us to make informed predictions of the sign of ΔS for various chemical and physical processes as illustrated in Example 2.

Example 2

Predicting the Sign of ∆S

Predict the sign of the entropy change for the following processes. Indicate the reason for each of your predictions.

  1. One mole liquid water at room temperature  ⟶  one mole liquid water at 50 °C
  2. Ag+(aq) + Cl–(aq)  →  AgCl(s)
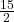  3. C6H6(ℓ) + \frac{15}{2}O2(g)  →  6 CO2(g) + 3 H2O(ℓ)
  4. NH3(s)  →  NH3(ℓ)

Solution

  1. positive, temperature increases
  2. negative, reduction in the number of ions (particles) in solution
  3. negative, net decrease in the amount of gaseous species
  4. positive, phase transition from solid to liquid, net increase in dispersal of matter

Check Your Learning

Predict the sign of the enthalpy change for the following processes. Give a reason for your prediction.

  1. NaNO3(s)  →  Na+(aq) + NO3–(aq)
  2. the freezing of liquid water
  3. CO2(s)  →  CO2(g)
  4. CaCO3(s)  →  CaO(s) + CO2(g)

Answer

  1. Positive; The solid dissolves to give an increase of mobile ions in solution.
  2. Negative; The liquid becomes a more ordered solid.
  3. Positive; The relatively ordered solid becomes a gas.
  4. Positive; There is a net production of one mole of gas.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103 Resource Book Copyright © by Chem 103 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book