Calorimetry
One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. In a calorimetry experiment, measurements of temperature changes are made inside a calorimeter, a calibrated device with a known heat capacity. The data can then be used to calculate the amount of heat transferred.
The measurement of heat transfer using this approach requires the definition of a system (the substance(s) undergoing the chemical or physical change) and its surroundings (the other components of the measurement apparatus that serve to either provide heat to the system or absorb heat from the system). Knowledge of the heat capacity of the surroundings, and careful measurements of the masses of the system and surroundings and their temperatures before and after the process, allows one to calculate the heat transferred as described in this section.
Heat flow when hot metals are placed in water
Let us first consider a simple example that illustrates the core idea behind calorimetry.
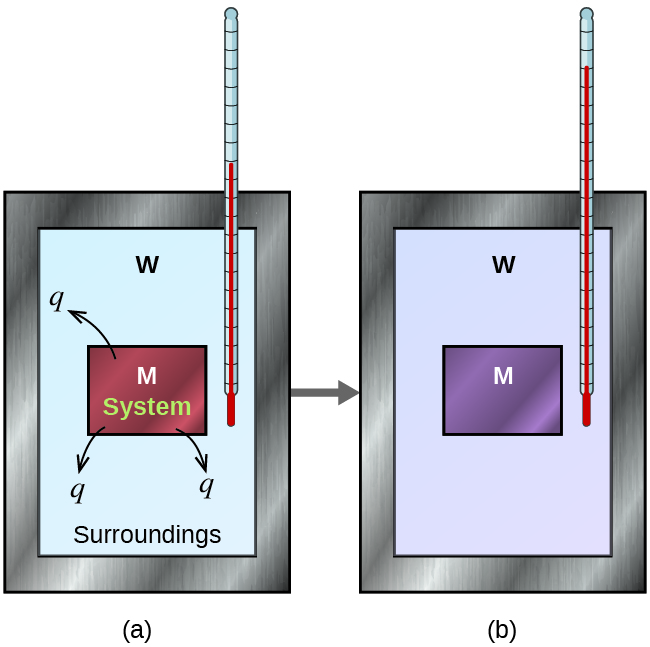 Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If they are brought into contact, heat will flow from metal to water. The temperature of the metal will decrease, and the temperature of the water will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium.
Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If they are brought into contact, heat will flow from metal to water. The temperature of the metal will decrease, and the temperature of the water will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium.
If this occurs in an ideal calorimeter, all of the heat transfer would occur between the two substances and no heat is gained or lost by the calorimeter or the environment outside of the calorimeter. In other words, the net heat change is zero:
qmetal + qwater = 0
In this example, we can define the metal as the system and the water as the surrounding. Rearranging the above equation shows that:
qmetal = –qwater
The magnitude of the heat (change) is therefore the same for system and surrounding (the amount of heat gained by the water as it warms is the same as the amount of heat lost by the metal as it cools). The negative sign in front of qwater merely shows that it is opposite in direction of heat flow as qmetal, but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition).
Example 1
A 360 g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (Specific Heat Table), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).
Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” elsewhere, then heat given off by rebar = −heat taken in by water, or:
qrebar = –qwater
Since we know how heat is related to other measurable quantities, we have:
(c × m × ∆T)rebar = -(c × m × ∆T)water
Letting f = final and i = initial, in expanded form, this becomes:
crebar × mrebar × (Tf, rebar – Ti, rebar) = -cwater × mwater × (Tf, water– Ti, water)
The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:
(0.449 J/(g·°C))(360 g)(42.7 °C – Ti, rebar) = (4.184 J/(g·°C))(425 g)(42.7 °C – 24.0 °C)
![]()
Solving this gives Ti, rebar = 248 °C, so the initial temperature of the rebar was 248 °C.
Check Your Learning
A 248 g piece of copper is dropped into 390 mL of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.
Answer
The initial temperature of the copper was 335.6 °C.
This method can also be used to determine other quantities, such as the specific heat of an unknown metal.
Example 2
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.
Solution
Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:
qmetal + qwater = 0
In expanded form, this is:
cmetal × mmetal × (Tf, metal – Ti, metal) = -cwater × mwater × (Tf, water – Ti, water)
Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C; and that for water, 60.0 mL = 60.0 g; we have:
(cmetal)(59.7 g)(28.5 °C – 100.0 °C) = -(4.184 J/(g·°C))(60.0 g)(28.5 °C – 22.0 °C)
Solving for cmetal gives:
![]()
Comparing this with values in the Specific Heats Table, our experimental specific heat is closest to the value for copper (0.39 J/(g·°C)), so we identify the metal as copper.
Check Your Learning
A 92.9 g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 mL of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).
Answer
cmetal = 0.13 J/(g·°C)
This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.
Heat flow when chemical reactions occur
When an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases the solution’s temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases the solution’s temperature (Figure 1). This temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in the chemical reaction.
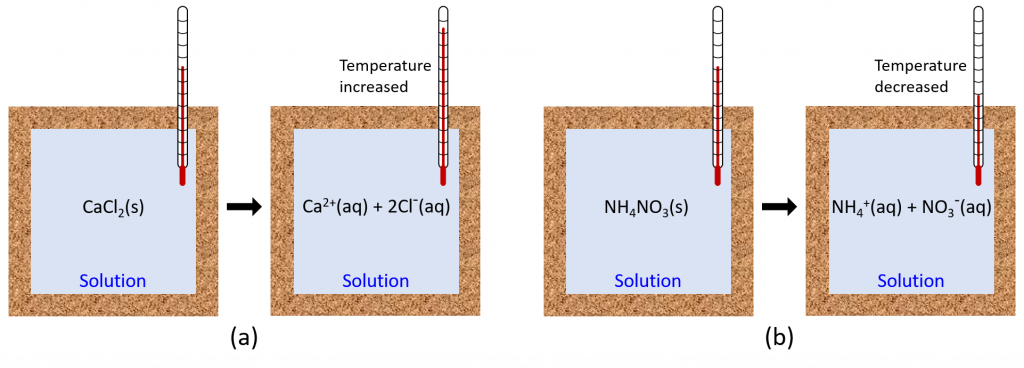
Oftentimes, we do not have a clear boundary between the chemical reaction and the solution in which it occurs (the chemical compounds are typically well-dispersed throughout the solution). Hence, we define the entire reaction solution as the system. If the experiment is conducted within an ideal calorimeter, then heat lost to matter outside the calorimeter (the surroundings) is zero, and:
qsystem = 0 = qreaction + qsolution
This means that the amount of heat produced or consumed by the reaction equals the amount of heat absorbed or lost by the solution:
qreaction = -qsolution
This equation will be extremely useful with heat-transfer related problems.
Demonstration: Heat of neutralization reaction
Set up. The following demonstration illustrates using calorimetry to measure the heat of the neutralization reaction between HCl and NaOH. First, HCl is added to an insulated container and the temperature probe is placed into the solution. An initial temperature reading is recorded on the computer. The lid is briefly lifted and the NaOH is added. The lid is then quickly replaced and the temperature change is observed.
Prediction. Before watching the video, write the reaction equation for this neutralization reaction.
Explanation. The reaction occurring here is:
HCl(aq) + NaOH(aq) → H2O(ℓ) + NaCl(aq)
The initial temperature reading of the HCl was stabilized at 22.4 °C. When the NaOH is added, the temperature of the solution increases to 66.3 °C. Since the temperature of the solution increased, we know that the qsolution is positive (positive ΔT) and therefore the qreaction must be negative. This indicates that the reaction is an exothermic reaction. An exothermic reaction releases energy and thus increases the temperature of the solution.
Note: If you look closely at the temperature reading at the end of the video, you’ll notice that the temperature reaches a maximum of 66.3 °C, but then starts to decrease again and reaches 65.7 °C at the end of the video. This decrease in temperature that happens after the reaction occurs is due to heat escaping from the insulated container. When you perform similar experiments in the lab, you will want to note the highest (or lowest) temperature reached for the reaction since imperfect insulation of the container causes the temperature to drop (or increase) after the reaction is completed and is not a result of the thermochemistry of the reaction being studied.
Example 3
When 50.0 mL of 0.10 M HCl(aq) and 50.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. What is the approximate amount of heat produced by this reaction?
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(ℓ)
Solution
To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C.
The heat given off by the reaction is equal to that absorbed by the solution. Therefore:
qreaction = –qsolution
(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange the surroundings outside of the calorimeter.)
Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:
qsolution = (c × m × ΔT)solution
To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 102 g (two significant figures). The specific heat of water is approximately 4.18 J/g °C, so we use that for the specific heat of the solution. Substituting these values gives:
qsolution = (4.184 J/(g·°C))(1.0 × 102 g)(28.9 °C – 22.0 °C) = 2.89 × 103 J
Finally, since we are trying to find the heat of the reaction, we have:
qreaction = –qsolution = -2.89 × 103 J
The negative sign indicates that the reaction is exothermic. It produces 2.89 kJ of heat.
Check Your Learning
When 100 mL of 0.200 M NaCl(aq) and 100 mL of 0.200 M AgNO3(aq), both at 21.9 °C, are mixed in a calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. How much heat is produced by this precipitation reaction? What assumptions did you make to determine your value?
Answer
1.34 × 103 J; assume no heat is absorbed by the calorimeter, no heat is lost to the surroundings outside of the calorimeter, and that the specific heat and mass of the solution are the same as those for water.
Chemistry in Real Life: Thermochemistry of Hand Warmers
When working or playing outdoors on a cold day, you might use a hand warmer to warm your hands. A common reusable hand warmer contains a supersaturated solution of NaC2H3O2 (sodium acetate) and a metal disc. Bending the disk creates nucleation sites around which the NaC2H3O2 quickly crystallizes (a later chapter on solutions will investigate saturation and supersaturation in more detail).
The process
NaC2H3O2(aq) → NaC2H3O2(s)
is exothermic, and the heat produced by this process is absorbed by your hands, thereby warming them (at least for a while). If the hand warmer is reheated, the NaC2H3O2 redissolves and can be reused.

Another common hand warmer produces heat when it is ripped open, exposing iron and water in the hand warmer to oxygen in the air. One simplified version of this exothermic reaction is
2Fe(s) + ![]() O2(g) → Fe2O3(s)
O2(g) → Fe2O3(s)
Salt in the hand warmer catalyzes the reaction, so it produces heat more rapidly; cellulose, vermiculite, and activated carbon help distribute the heat evenly. Other types of hand warmers use lighter fluid (a platinum catalyst helps lighter fluid oxidize exothermically), charcoal (charcoal oxidizes in a special case), or electrical units that produce heat by passing an electrical current from a battery through resistive wires.
Example 4

When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack” (Figure 3). When 3.21 g of solid NH4NO3 dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature of the solution decreases to 20.3 °C.
Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.
Solution
We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:
qreaction = –qsolution
Assuming also that the specific heat of the solution is the same as that for water, we have:
qreaction = –qsolution = -(c × m × ΔT)solution
qreaction = -[(4.184 J/(g·°C)) × (53.2 g) × (20.3 °C – 24.9 °C)]
= -[(4.184 J/(g·°C)) × (53.2 g) × (-4.6 °C)]
= +1.0 × 103 J = +1.0 kJ
The positive sign for qreaction indicates that the dissolution is an endothermic process.
Check Your Learning
When a 3.00-g sample of KCl was added to 3.00 × 102 g of water in a calorimeter, the temperature decreased by 1.05 °C. How much heat is involved in the dissolution of the KCl? What assumptions did you make?
Answer
1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat of the solution is the same as that for water.
Coffee Cup Calorimetry
Scientists use well-insulated calorimeters to minimize the transfer of heat to the environment outside of the calorimeter. This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on.
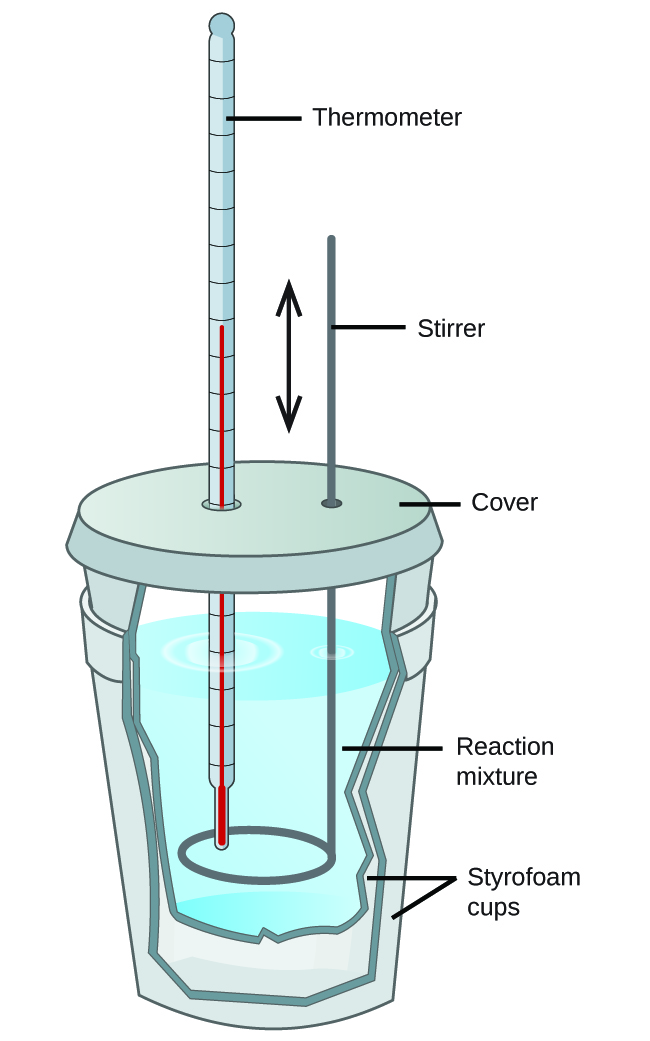 Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal loss during use, along with an insulated cover, handheld stirrer, and simple thermometer. Many general chemistry labs utilize such coffee cup calorimeters because they are inexpensive and easy to use. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it.
Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal loss during use, along with an insulated cover, handheld stirrer, and simple thermometer. Many general chemistry labs utilize such coffee cup calorimeters because they are inexpensive and easy to use. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it.
These types of calorimeters operate at constant pressure as the lid is not an air-tight seal and the system is effectively still open to the atmosphere. Since the heat flow that is measured in this case is the heat flow at constant pressure, qp, this type of calorimeter provides a direct way to find the enthalpy change of the process, ΔH, since ΔH = qp.
Commercial solution calorimeters are more expensive. Calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor.

