Energy Changes in Reactions
Reactions and Energy
Every physical and chemical change involves energy changes as well. For example, when water is boiled and evaporated, heat must be added to the liquid water to form gaseous water. In this example, the process is endothermic, meaning that it requires energy.
H2O(ℓ) + energy ⟶ H2O(g)
Conversely, when liquid water freezes to form ice, heat is lost during this process. In this example, the process is exothermic, meaning that it releases energy.
H2O(ℓ) ⟶ H2O(s) + energy
Like other quantities in balanced chemical equations, energy scales with the amount of reactants used and products formed. We can examine the combustion and electrolysis of water (two chemical changes) to see this scaling.
Demonstration: Energy can be released in the form of sound, light, and heat
Set up. Combustion of hydrogen gas in the presence of oxygen is an exothermic process. This demonstration shows the combustion of a balloon filled with hydrogen gas and oxygen gas.
Explanation. The combustion of the hydrogen and oxygen gases causes an explosion that releases energy. This energy can be observed in the forms of sound, light, and heat. When more hydrogen gas is used in the second explosion, the explosion releases even more energy.
Intuitively, one would predict that if we ignited a larger balloon filled with more hydrogen and oxygen that the explosion would be larger. In chemistry terms, more energy would be released. Conversely, if we ignited a balloon with less hydrogen and oxygen then the explosion would be smaller. Again, in chemistry terms, less energy would be released. In other words, the energy scales with reaction stoichiometry.
2 H2(g) + O2(g) ⟶ 2 H2O(ℓ) + energy
One can carefully quantify this energy released. When two moles of hydrogen gas combust in the presence of one mole of oxygen gas, then two moles of liquid water are formed and 483.6 kJ of energy are released.
2 H2(g) + O2(g) ⟶ 2 H2O(ℓ) + 483.6 kJ
If we double the amount of reactants, then we double the products, including the amount of energy released:
4 H2(g) + 2 O2(g) ⟶ 4 H2O(ℓ) + 967.2 kJ
Enthalpy
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is a state function (the value of a state function depends only on the state that a system is in, and not on how that state is reached). Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (ΔH) is the heat of reaction at constant pressure (qp). If a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (qp) and enthalpy change (ΔH) for the process are equal.
The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with qp = ΔH. Determining qp in a calorimeter by measuring the heat exchanged with the surroundings will therefore lead directly to the determination of ΔH for the process taking place in the calorimeter. Using an analogy involving money may help you understand this better. If you withdraw $100 from your bank account (analogous to qp) you can actually count the money you receive. This is what happens in a calorimeter, although it is the Joules of heat that are determined as a reaction occurs. You might not actually know the exact amount of money in your bank account, but your bank balance will have decreased by exactly $100. This is analogous to the enthalpy change. Initial enthalpy values of reactants and final enthalpy values of products, like the bank balance in this example, are not known and nor do they have to be, in order to determine the change or difference between them, ΔH.
The following conventions apply when we use ΔH:
- Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. For example, consider this equation:
2 H2(g) + O2(g) → 2 H2O(ℓ) ΔH = -9.50 × 10-22 kJ = -572 kJ/mol
This refers to reaction of 2 molecules of hydrogen gas with 1 molecule of oxygen gas to form 2 molecules of liquid water, at some temperature and pressure. If this reaction equation took place once, the two hydrogen molecules and the one oxygen molecule would react to form two water molecules and 9.5 × 10−22 kJ would be transferred to the surroundings.
Because we are interested in laboratory-scale reactions, where moles of reactants are involved, ΔH is always reported per mole of reaction rather than for a single reaction event. A mole of reaction involves a chemical reaction equation happening 6.022 × 1023 times. In this case, that is 2 moles of H2(g) reacting with 1 mole of O2(g) to give 2 moles of H2O(ℓ), yielding:
(-9.50 × 10−22 kJ) × (6.022 × 1023 mol−1) = -572 kJ/mol
Because the ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation, if the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor (ΔH is an extensive property):
(two-fold increase in amounts)
4 H2(g) + 2 O2(g) → 4 H2O(ℓ) ΔH = 2 × (-572 kJ/mol) = -1144 kJ/mol of reaction as written
(two-fold decrease in amounts)
H2(g) + ½ O2(g) → H2O(ℓ) ΔH = ½ × (-572 kJ/mol) = -286 kJ/mol of reaction as written
- The enthalpy change of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and ½ mole of oxygen gas react to form 1 mole of liquid water, 286 kJ/mol of heat are released. If gaseous water forms, only 242 kJ/mol of heat are released.
H2(g) + ½ O2(g) → H2O(g) ΔH = -242 kJ/mol
- A negative value of an enthalpy change, ΔH, indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
H2O(ℓ) → H2(g) + ½ O2(g) ΔH = -1 × (-286 kJ/mol) = +286 kJ/mol
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.
Example 1
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ of heat are produced (released). Determine the enthalpy change for the reaction
C12H22O11(aq) + 8 KClO3(aq) → 12 CO2(g) + 11 H2O(ℓ) + 8 KCl(aq)
Solution
We have available
2.67 g × ![]() = 0.00780 mol C12H22O11
= 0.00780 mol C12H22O11
and
7.19 g × ![]() = 0.0587 mol KClO3
= 0.0587 mol KClO3
0.0587 mol KClO3 × ![]() = 0.00734 mol C12H22O11 is needed; C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
= 0.00734 mol C12H22O11 is needed; C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
The reaction uses 8 mol KClO3, and the conversion factor is ![]() , so we have
, so we have
ΔH = ![]() = -5960 kJ/mol
= -5960 kJ/mol
The enthalpy change for this reaction is -5960 kJ/mol, and the thermochemical equation is:
C12H22O11(aq) + 8 KClO3(aq) → 12 CO2(g) + 11 H2O(ℓ) + 8 KCl(aq) ΔH = -5960 kJ/mol
Check Your Learning
When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl2(s) and 8.60 kJ of heat is produced. What is the enthalpy change for the reaction when 1 mole of FeCl2(s) is produced?
Answer
ΔH = -338 kJ/mol
Calculating Enthalpy Change
The enthalpy change, ΔH, for a chemical reaction is approximately equal to the sum of the energy required to break all bonds in the reactants (energy “in”, positive sign) plus the energy released when all bonds are formed in the products (energy “out,” negative sign). This can be expressed mathematically in the following way:
ΔHreaction = ∑ (energy of bonds broken) – ∑ (energy of bonds formed)
In this expression, the symbol Ʃ means “the sum of” and we sum the bond energy in kilojoules per mole, which is always a positive number. The bond energy is obtained from a table (like the one below) and will depend on whether the particular bond is a single, double, or triple bond.
Average Bond Enthalpy
In kJ/mol
| I | Br | Cl | S | P | Si | F | O | N | C | H | |
| H | 299 | 366 | 431 | 347 | 322 | 323 | 566 | 467 | 391 | 416 | 436 |
| C | 213 | 285 | 327 | 272 | 264 | 301 | 485 | 358 | 285 | 346 | |
| N | - | - | 193 | - | ~200 | 335 | 272 | 201 | 160 | ||
| O | 201 | - | 205 | - | ~340 | 368 | 190 | 146 | |||
| F | - | 238 | 255 | 326 | 490 | 582 | 158 | ||||
| Si | 234 | 310 | 391 | 226 | - | 226 | |||||
| P | 184 | 264 | 319 | - | 209 | ||||||
| S | - | 213 | 255 | 226 | Multiple Bonds | Multiple Bonds | |||||
| Cl | 209 | 217 | 242 | N=N | 418 | C=C | 598 | ||||
| Br | 180 | 193 | N≡N | 946 | C≡C | 813 | |||||
| I | 151 | C=N | 616 | C=O in CO2 | 803 | ||||||
| C≡N | 866 | C=O carbonyl | 695 | ||||||||
| N=O | 607 | C≡O | 1073 | ||||||||
| O=O in O2 | 498 | N≡O | 632 | ||||||||
| Data from Cotton, F.A., Wilkinson, G. and Gaus, P.L., Basic Inorganic Chemistry, 3rd ed., New York: Wiley, 1995. Corrected values for C-C and C-O from Cottrell, T.L., The Strengths of Chemical Bonds, 2ed., London:Butterworths, 1958. |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Thus, in calculating enthalpies in this manner, it is important that we consider the bonding in all reactants and products. Because bond energy values are typically averages for one type of bond in many different molecules, this calculation provides a rough estimate, not an exact value, for the enthalpy of reaction.
Consider the following reaction:
H2(g) + Cl2(g) → 2 HCl(g)
or
H-H(g) + Cl-Cl(g) → 2 H-Cl(g)
To form two moles of HCl, one mole of H–H bonds and one mole of Cl–Cl bonds must be broken. The energy required to break these bonds is the sum of the bond energy of the H–H bond (436 kJ/mol) and the Cl–Cl bond (242 kJ/mol). During the reaction, two moles of H–Cl bonds are formed (bond energy = 431 kJ/mol), releasing 2 × 431 kJ; or 862 kJ. Because the bonds in the products are stronger than those in the reactants, the reaction releases more energy than it consumes:
| ΔHreaction | = | ∑ (energy of bonds broken) – ∑ (energy of bonds formed) |
| = | [(H-H) + (Cl-Cl)] – [2(H-Cl)] | |
| = | [436 kJ/mol + 242 kJ/mol] – [2(431 kJ/mol)] | |
| = | -184 kJ/mol |
This excess energy is released as heat, so the reaction is exothermic.
Example 2
Methanol, CH3OH, may be an excellent alternative fuel. The high-temperature reaction of steam and carbon produces a mixture of the gases carbon monoxide, CO, and hydrogen, H2, from which methanol can be produced. Using the bond energies in the Table above, calculate the approximate enthalpy change, ΔH, for the reaction here:
CO(g) + 2 H2(g) → CH3OH(g)
Solution
First, we need to write the Lewis structures of the reactants and the products:

From this, we see that ΔH for this reaction involves the energy required to break a C–O triple bond and two H–H single bonds, as well as the energy produced by the formation of three C–H single bonds, a C–O single bond, and an O–H single bond. We can express this as follows:
ΔH = ∑ (energy of bonds broken) – ∑ (energy of bonds formed)
ΔH = [(C≡O) + 2(H-H)] – [3(C-H) + (C-O) + (O-H)]
Using the bond energy values in the Table above, we obtain:
ΔH = [1073 kJ/mol + 2(436 kJ/mol)] – [3(416 kJ/mol) + 358 kJ/mol + 467 kJ/mol]
ΔH = -128 kJ/mol
Check Your Learning
Ethyl alcohol, CH3CH2OH, was one of the first organic chemicals deliberately synthesized by humans. It has many uses in industry, and it is the alcohol contained in alcoholic beverages. It can be obtained by the fermentation of sugar or synthesized by the hydration of ethylene in the following reaction:
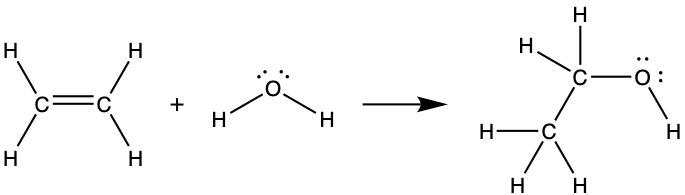
Using the bond energies in the table above, calculate an approximate enthalpy change, ΔH, for this reaction.
Answer:
–55 kJ/mol

