"

Orbital Energies, Spin, and Electron Configurations

Spin Quantum Number

It was demonstrated in the 1920s that when hydrogen line spectra are examined at extremely high resolution, some lines are actually not single peaks but rather pairs of closely spaced lines. This is the so-called fine structure of the spectrum, and it implies that there are additional small differences in energies of electrons even when they are located in the same orbital. These observations led Samuel Goudsmit and George Uhlenbeck to propose that electrons have a fourth quantum number. They called this the spin quantum number, or ms.

The other three quantum numbers—n, l, and ml—are properties of specific atomic orbitals that define the most likely location in space of an electron. These orbitals are a result of solving the Schrödinger equation for electrons in atoms. The electron spin is a different kind of property. It is a completely quantum phenomenon with no analogues in the classical realm. In addition, it cannot be derived from solving the Schrödinger equation and is not related to the normal spatial coordinates (such as the Cartesian x, y, and z). Electron spin describes an intrinsic electron “rotation” or “spinning.” Each electron acts as a tiny magnet, just as if it were a tiny rotating object charged with an angular momentum, even though this rotation cannot be observed in terms of the spatial coordinates.

The magnitude of the overall electron spin can only have one value, and an electron can only “spin” in one of two quantized states. One is termed the α state, with the z component of the spin being in the positive direction of the z axis. This corresponds to the spin quantum number ms = +½. The other is called the β state, with the z component of the spin being negative and ms = -½. Any electron, regardless of the atomic orbital it is located in, can only have one of those two values of the spin quantum number. The energies of electrons having ms = -½ and ms = ½ are different if an external magnetic field is applied.

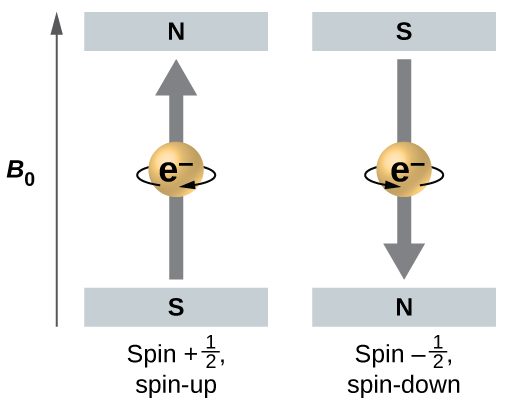
This diagram has an upward pointing arrow at the left which is labeled, “B subscript 0.” To the right, two spheres are shown. The first has a gray square at the top labeled, “N,” and a second gray square at the bottom labeled, “S.” A curved arrow is pointing right across the surface of the sphere and a gray arrow points upward through the center of the sphere. This sphere is labeled, “Spin plus one-half, spin-up.” The sphere just to the right has a gray square above it labeled, “S,” and a gray square below it labeled, “N.” This sphere has a curved arrow on its surface that is directed to the left and a gray arrow through the center of the sphere that points downward. This sphere is labeled, “Spin negative one-half spin-down.”
Figure 1. Electrons with spin values ±½ in an external magnetic field.

Figure 1 illustrates this phenomenon. An electron acts like a tiny magnet. Its moment is directed up (in the positive direction of the z axis) for the +½ spin quantum number and down (in the negative z direction) for the -½ spin quantum number. A magnet has a lower energy if its magnetic moment is aligned with the external magnetic field (the left electron in Figure 1) and a higher energy for the magnetic moment being opposite to the applied field. This is why an electron with ms = +½ has a slightly lower energy in an external field in the positive z direction, and an electron with ms = -½ has a slightly higher energy in the same field. This is true even for an electron occupying the same orbital in an atom. A spectral line corresponding to a transition for electrons between the same orbitals but with different spin quantum numbers has two possible values of energy; thus, the line in the spectrum will show a fine structure splitting.

The Pauli Exclusion Principle

An electron in an atom is completely described by four quantum numbers: n, l, ml, and ms. The first three quantum numbers define the orbital and the fourth quantum number describes the intrinsic electron property called spin. An Austrian physicist Wolfgang Pauli formulated a general principle that gives the last piece of information that we need to understand the general behavior of electrons in atoms. The Pauli exclusion principle can be formulated as follows: No two electrons in the same atom can have exactly the same set of all four quantum numbers. What this means is that electrons can share the same orbital (the same set of the quantum numbers n, l, and ml), but only if their spin quantum numbers, ms, have different values. Since the spin quantum number can only have two values (± ½), no more than two electrons can occupy the same orbital (and if two electrons are located in the same orbital, they must have opposite spins). Therefore, any atomic orbital can be populated by only zero, one, or two electrons.

The properties and meaning of the quantum numbers of electrons in atoms are briefly summarized in Table 1.

Table 1. Quantum numbers, their properties, and significance
Name Symbol Allowed values Physical meaning
principal quantum number n 1, 2, 3, 4, …. shell, the general region of an electron in the orbital (distance away from the nucleus)
azimuthal (or angular momentum) quantum number l 0 ≤ l ≤ n–1 subshell, the shape of the orbital
magnetic quantum number ml – l ≤ ml ≤ l orientation of the orbital
spin quantum number ms +½, −½ direction of the intrinsic quantum “spinning” of the electron
Example 1: Maximum Number of Electrons

Calculate the maximum number of electrons that can occupy a shell with (a) n = 2, (b) n = 5, and (c) n as a variable. Note you are only looking at the orbitals with the specified n value, not those at lower energies.

Solution

(a) When n = 2, there are four orbitals (a single orbital with l = 0, and three orbitals labeled l = 1). These four orbitals can contain eight electrons.

(b) When n = 5, there are five subshells of orbitals that we need to sum:

1 orbital with l = 0
3 orbitals with l = 1
5 orbitals with l = 2
7 orbitals with l = 3
+ 9 orbitals with l = 4
———————————————
25 orbitals total

Again, each orbital holds two electrons, so 50 electrons can fit in this shell.

(c) The number of orbitals in any shell n will equal n2. There can be up to two electrons in each orbital, so the maximum number of electrons will be 2 × n2

Check Your Learning

If a shell contains a maximum of 32 electrons, what is the principal quantum number, n?

Answer

n = 4

Orbital Energies

Single Electron

Figure 2. Orbital energy level diagram for the hydrogen atom. Each box corresponds to one orbital. Note that the difference in energy between orbitals decreases rapidly with increasing values of n.

Although we have discussed the shapes of orbitals, we have said little about their comparative energies. We begin our discussion of orbital energies by considering atoms or ions with only a single electron (such as H or He+). This is the simplest case.

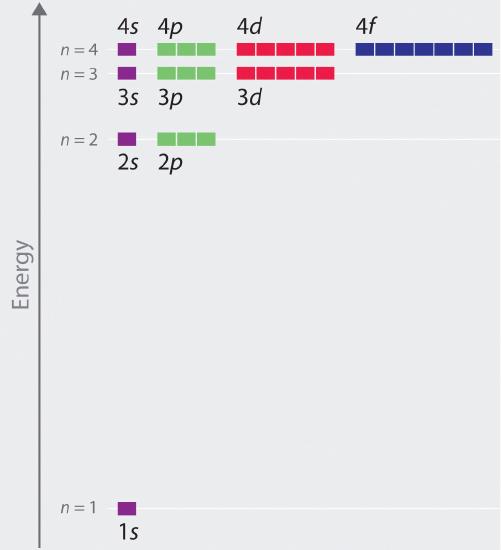
The relative energies of the atomic orbitals with n ≤ 4 for a hydrogen atom are plotted in Figure 2. Note that the orbital energies depend on only the principal quantum number n, not on l. Consequently, the energies of the 2s and 2p orbitals of hydrogen are the same; the energies of the 3s, 3p, and 3d orbitals are the same; and so forth. The orbital energies obtained for hydrogen using quantum mechanics are exactly the same as the allowed energies calculated by Bohr. In contrast to Bohr’s model, however, which allowed only one orbit for each energy level, quantum mechanics predicts that there are 4 orbitals with different electron density distributions in the n = 2 principal shell (one 2s and three 2p orbitals), 9 in the n = 3 principal shell, and 16 in the n = 4 principal shell. As we have just seen, quantum mechanics predicts that in the hydrogen atom, all orbitals with the same value of n (e.g., the three 2p orbitals) are degenerate, meaning that they have the same energy. Figure 2 shows that the energy levels become closer and closer together as the value of n increases, as expected because of the 1/n2 dependence of orbital energies.

Two or More Electrons

The energy of atomic orbitals increases as the principal quantum number, n, increases. In any atom with two or more electrons, the repulsion between the electrons makes energies of subshells with different values of l differ so that the energy of the orbitals increases within a shell in the order s < p < d < f. Figure 3 depicts the trends of increasing energy with increasing n and increasing l (note that this is different than the orbital diagram for hydrogen in Figure 2 because now we have more than one electron).

A table entitled, “Subshell electron capacity,” is shown. Along the left side of the table, an upward pointing arrow labeled, “E,” is drawn. The table includes three columns. The first column is narrow and is labeled, “2.” The second is slightly wider and is labeled, “6.” The third is slightly wider yet and is labeled, “10.” The fourth is the widest and is labeled, “14.” The first column begins at the very bottom with a horizontal line segment labeled “1 s.” Evenly spaced line segments continue up to 7 s near the top of the column. In the second column, a horizontal dashed line segment labeled, “2 p,” appears at a level between the 2 s and 3 s levels. Similarly 3 p appears at a level between 3 s and 4 s, 4 p appears just below 5 s, 5 p appears just below 6 s, and 6 p appears just below 7 s. In the third column, a dashed line labeled, “3 d,” appears just below the level of 4 p. Similarly, 4 d appears just below 5 p and 5 d appears just below 6 p. Six d however appears above the levels of both 6 p and 7 s. The far right column entries begin with a dashed line labeled, “4 f,” positioned at a level just below 5 d. Similarly, a second dashed line segment appears just below the level of 6 d, which is labeled, “5 f.”
Figure 3. Generalized energy-level diagram for atomic orbitals in an atom with two or more electrons (not to scale).

The 1s orbital at the bottom of Figure 3 is the orbital with electrons of lowest energy. The energy increases as we move up to the 2s and then 2p, 3s, and 3p orbitals, showing that the increasing n value has more influence on energy than the increasing l value for small atoms. However, this pattern does not hold for larger atoms. For example, the 3d orbital is higher in energy than the 4s orbital. Such overlaps continue to occur frequently as we move up the chart.

Electrons in successive atoms on the periodic table tend to fill low-energy orbitals first. Thus, many students find it confusing that, for example, the 5p orbitals fill immediately after the 4d, and immediately before the 6s. The filling order is based on observed experimental results, and has been confirmed by theoretical calculations. As the principal quantum number, n, increases, the size of the orbital increases and the electrons spend more time farther from the nucleus. Thus, the attraction to the nucleus is weaker and the energy associated with the orbital is higher (less stabilized). But this is not the only effect we have to take into account. Within each shell, as the value of l increases, the electrons are less penetrating (meaning there is less electron density found close to the nucleus), in the order s > p > d > f. Electrons that are closer to the nucleus slightly repel electrons that are farther out, offsetting the more dominant electron–nucleus attractions slightly (recall that all electrons have −1 charges, but nuclei have +Z charges).

This phenomenon is called shielding and will be discussed in more detail later. Electrons in orbitals that experience more shielding are less stabilized and thus higher in energy. For small orbitals (1s through 3p), the increase in energy due to n is more significant than the increase due to l; however, for larger orbitals the two trends are comparable and cannot be simply predicted.

Electron Configurations of Atoms

The arrangement of electrons in the orbitals of an atom is called the electron configuration of the atom. We describe an electron configuration with a symbol that contains three pieces of information (Figure 4):

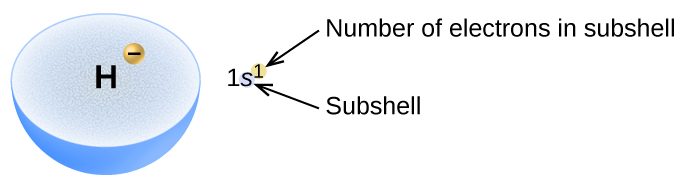
A light blue hemisphere is labeled H. At a location about midway between the center and outer edge of the hemisphere, a small yellow-orange sphere is shown that is labeled with a negative sign. To the right of this diagram is the electron configuration 1 s superscript 1. The superscript is shown in a small yellow-orange circle. This superscript is labeled, “Number of electrons in subshell,” and the s is labeled, “Subshell.”
Figure 4. The diagram of an electron configuration specifies the subshell (n and l value, with letter symbol) and superscript number of electrons.
  1. The number of the principal quantum number, n,
  2. The letter that designates the orbital type (the subshell, l), and
  3. A superscript number that designates the number of electrons in that particular subshell.

For example, 2p4 indicates four electrons in a p subshell (l = 1) with a principal quantum number (n) of 2. The notation 3d8 (read “three–d–eight”) indicates eight electrons in the d subshell (l = 2) of the principal shell for which n = 3.

The Aufbau Principle

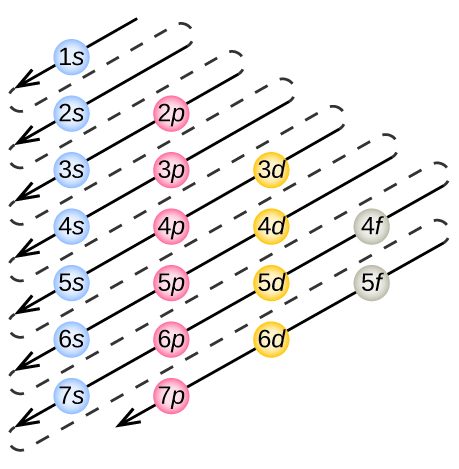
This figure includes a chart used to order the filling of electrons into atoms. At the top is a blue circle labeled “1 s.” In a row beneath this circle are 6 additional blue circles labeled “2 s” through “7 s.” A column to the right begins just right of 2 s and contains pink circles labeled 2 p through 7 p. A column to the right begins just right of 3 p and contains yellow circles labeled 3 d through 6 d. No circles are placed to the right of the 7 s and 7 p circles. A final column on the right begins right of 4 d. It includes grey circles labeled, “4 f” and, “5 f.” No circles are placed right of 6 d. Through these circles, arrows are included in the figure pointing down and to the left. The first arrow begins in the upper right and passes through 1 s. The second arrow begins just below and passes through 2 s. The third arrow passes through 2 p and 3 s. The fourth arrow passes through 3 p and 4 s. This pattern of parallel arrows pointing downward to the left continues through all circles completing the pattern 1 s 2 s 2 p 3 s 3 p 4 s 3 d 4 p 5 s 4 d 5 p 6 s 4 f 5 d 6 p 7 s 5 f 6 d 7 p.
Figure 5. The arrow leads through each subshell in the appropriate filling order for electron configurations. This chart is straightforward to construct. Simply make a column for all the s orbitals with each n shell on a separate row. Repeat for p, d, and f. Be sure to only include orbitals allowed by the quantum numbers (no 1p or 2d, and so forth). Finally, draw diagonal lines from top to bottom as shown.

To determine the electron configuration for any particular atom, we can “build” the structures in the order of atomic numbers. Beginning with hydrogen, and continuing across the periods of the periodic table, we add one proton at a time to the nucleus and one electron to the proper subshell until we have described the electron configurations of all the elements. This procedure is called the Aufbau principle, from the German word Aufbau (“to build up”). Each added electron occupies the subshell of lowest energy available (in the order shown in Figure 3), subject to the limitations imposed by the allowed quantum numbers according to the Pauli exclusion principle. Electrons enter higher-energy subshells only after lower-energy subshells have been filled to capacity.

Figure 5 illustrates the traditional way to remember the filling order for atomic orbitals.

Since the arrangement of the periodic table is based on the electron configurations, Figure 6 provides an alternative method for determining the electron configuration. The filling order simply begins at hydrogen and includes each subshell as you proceed in increasing Z order. For example, after filling the 3p block up to Ar, we see the orbital will be 4s (K, Ca), followed by the 3d orbitals.

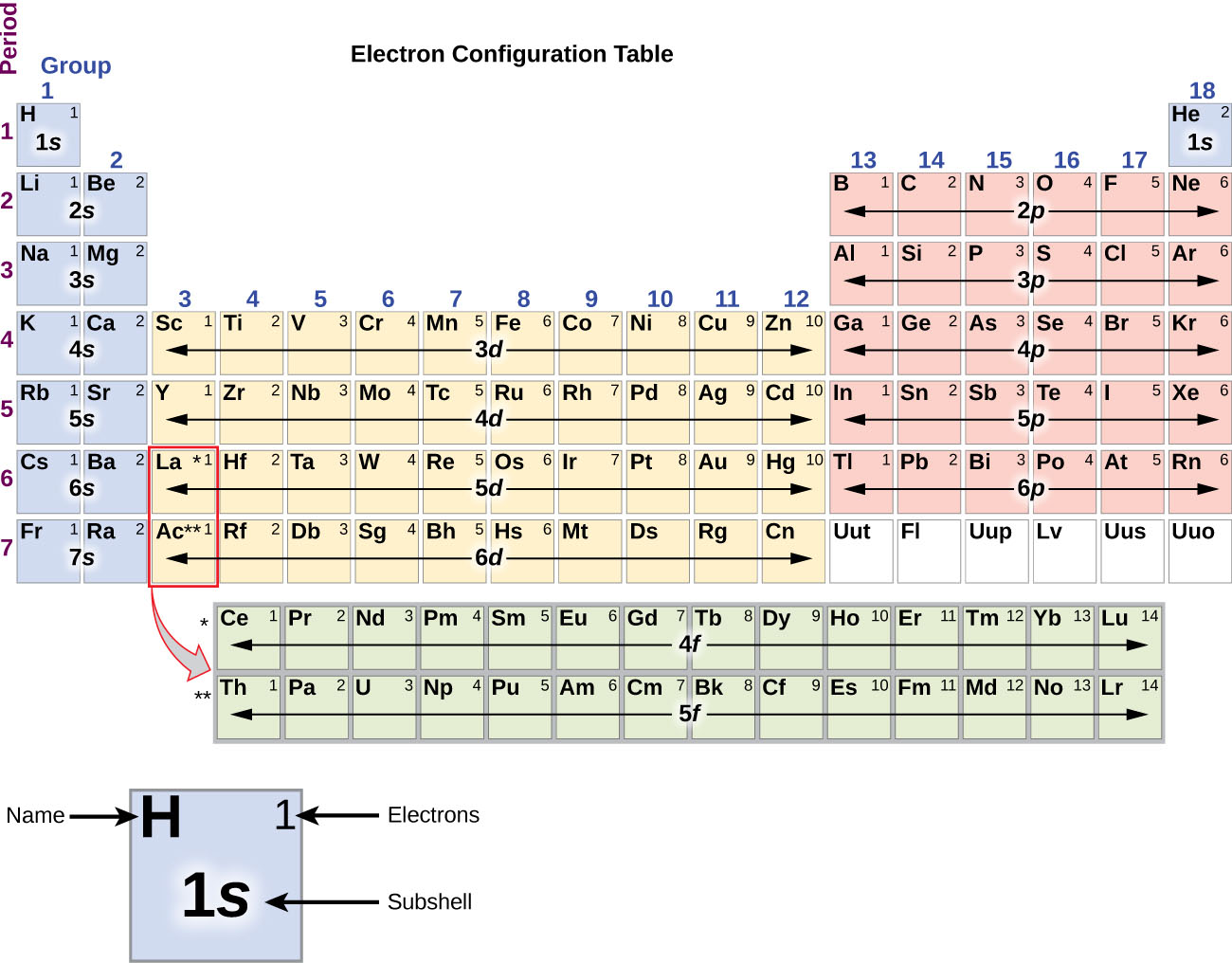
In this figure, a periodic table is shown that is entitled, “Electron Configuration Table.” Beneath the table, a square for the element hydrogen is shown enlarged to provide detail. The element symbol, H, is placed in the upper left corner. In the upper right is the number of electrons, 1. The lower central portion of the element square contains the subshell, 1 s. Helium and elements in groups 1 and 2 are shaded blue. In this region, the rows are labeled 1 s through 7 s moving down the table. Groups 3 through 12 are shaded orange, and the rows are labeled 3 d through 6 d moving down the table. Groups 13 through 18, except helium, are shaded pink and are labeled 2 p through 6 p moving down the table. The lanthanide and actinide series across the bottom of the table are shaded grey and are labeled 4 f and 5 f respectively.
Figure 6. This periodic table shows the electron configuration for each subshell. By “building up” from hydrogen, this table can be used to determine the electron configuration for any atom on the periodic table.

Writing Orbital Diagrams

We will now construct the ground-state electron configuration and orbital diagram for a selection of atoms in the first and second periods of the periodic table. Orbital diagrams are pictorial representations of the electron configuration, showing the individual orbitals and the pairing arrangement of electrons. We start with a single hydrogen atom (atomic number 1), which consists of one proton and one electron. Referring to Figure 5 or Figure 6, we would expect to find the electron in the 1s orbital. By convention, the ms  =  +½ value is usually filled first. The electron configuration and the orbital diagram are:

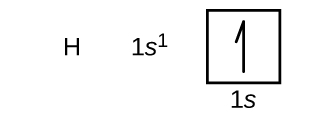
In this figure, the element symbol H is followed by the electron configuration is 1 s superscript 1. An orbital diagram is provided that consists of a single square. The square is labeled below as, “1 s.” It contains a single upward pointing half arrow.

Following hydrogen is the noble gas helium, which has an atomic number of 2. The helium atom contains two protons and two electrons. The first electron has the same four quantum numbers as the hydrogen atom electron (n = 1, l = 0, ml = 0, ms  =  +½). The second electron also goes into the 1s orbital and fills that orbital. The second electron has the same n, l, and ml quantum numbers, but must have the opposite spin quantum number, ms  =  -½. This is in accord with the Pauli exclusion principle: No two electrons in the same atom can have the same set of four quantum numbers. For orbital diagrams, this means two arrows go in each box (representing two electrons in each orbital) and the arrows must point in opposite directions (representing paired spins). The electron configuration and orbital diagram of helium are:

In this figure, the element symbol H e is followed by the electron configuration, “1 s superscript 2.” An orbital diagram is provided that consists of a single square. The square is labeled below as “1 s.” It contains a pair of half arrows: one pointing up and the other down.

The n = 1 shell is completely filled in a helium atom.

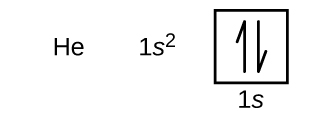
The next atom is the alkali metal lithium with an atomic number of 3. The first two electrons in lithium fill the 1s orbital and have the same sets of four quantum numbers as the two electrons in helium. The remaining electron must occupy the orbital of next lowest energy, the 2s orbital. Thus, the electron configuration and orbital diagram of lithium are:

In this figure, the element symbol L i is followed by the electron configuration, “1 s superscript 2 2 s superscript 1.” An orbital diagram is provided that consists of two individual squares. The first square is labeled below as, “1 s.” The second square is similarly labeled, “2 s.” The first square contains a pair of half arrows: one pointing up and the other down. The second square contains a single upward pointing arrow.

An atom of the alkaline earth metal beryllium, with an atomic number of 4, contains four protons in the nucleus and four electrons surrounding the nucleus. The fourth electron fills the remaining space in the 2s orbital.

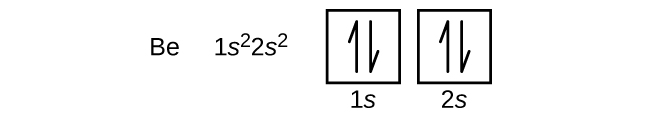
In this figure, the element symbol B e is followed by the electron configuration, “1 s superscript 2 2 s superscript 2.” An orbital diagram is provided that consists of two individual squares. The first square is labeled below as, “1 s.” The second square is similarly labeled, “2 s.” Both squares contain a pair of half arrows: one pointing up and the other down.

An atom of boron (atomic number 5) contains five electrons. The n = 1 shell is filled with two electrons and three electrons will occupy the n = 2 shell. Because any s subshell can contain only two electrons, the fifth electron must occupy the next energy level, which will be a 2p orbital. There are three degenerate 2p orbitals (ml = −1, 0, +1) and the electron can occupy any one of these p orbitals. When drawing orbital diagrams, we include empty boxes to depict any empty orbitals in the same subshell that we are filling.

In this figure, the element symbol B is followed by the electron configuration, “1 s superscript 2 2 s superscript 2 2 p superscript 1.” The orbital diagram consists of two individual squares followed by 3 connected squares in a single row. The first square is labeled below as, “1 s.” The second is similarly labeled, “2 s.” The connected squares are labeled below as, “2 p.” All squares not connected contain a pair of half arrows: one pointing up and the other down. The first square in the group of 3 contains a single upward pointing arrow.

Carbon (atomic number 6) has six electrons. Four of them fill the 1s and 2s orbitals. The remaining two electrons occupy the 2p subshell. We now have a choice of filling one of the 2p orbitals and pairing the electrons or of leaving the electrons unpaired in two different, but degenerate, p orbitals. The orbitals are filled as described by Hund’s rule: The lowest-energy configuration for an atom with electrons within a set of degenerate orbitals is that having the maximum number of unpaired electrons with parallel spins. Placing the electrons in different orbitals and with parallel spins tends to keep the electrons in different regions of space, thus minimizing their Coulomb repulsion and lowering the energy. Thus, the two electrons in the carbon 2p orbitals have identical n, l, and ms quantum numbers and differ in their ml quantum number (in accord with the Pauli exclusion principle). The electron configuration and orbital diagram for carbon are:

In this figure, the element symbol C is followed by the electron configuration, “1 s superscript 2 2 s superscript 2 2 p superscript 2.” The orbital diagram consists of two individual squares followed by 3 connected squares in a single row. The first blue square is labeled below as, “1 s.” The second is similarly labeled, “2 s.” The connected squares are labeled below as, “2 p.” All squares not connected to each other contain a pair of half arrows: one pointing up and the other down. The first two squares in the group of 3 each contain a single upward pointing arrow.

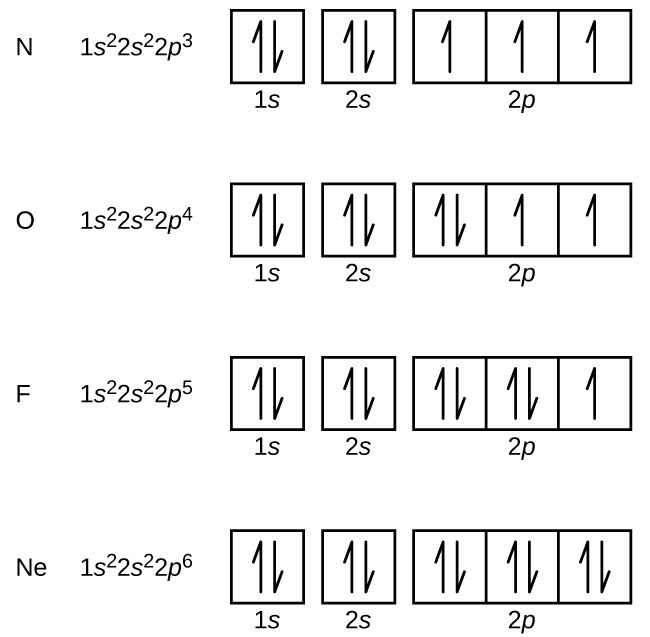
Nitrogen (atomic number 7) fills the 1s and 2s subshells and has one electron in each of the three 2p orbitals, in accordance with Hund’s rule. These three electrons have unpaired spins. Oxygen (atomic number 8) has a pair of electrons in any one of the 2p orbitals (the electrons have opposite spins) and a single electron in each of the other two. Fluorine (atomic number 9) has only one 2p orbital containing an unpaired electron. All of the electrons in the noble gas neon (atomic number 10) are paired, and all of the orbitals in the n = 1 and the n = 2 shells are filled. The electron configurations and orbital diagrams of these four elements are:

This figure includes electron configurations and orbital diagrams for four elements, N, O, F, and N e. Each diagram consists of two individual squares followed by 3 connected squares in a single row. The first square is labeled below as, “1 s.” The second is similarly labeled, “2 s.” The connected squares are labeled below as, “2 p.” All squares not connected to each other contain a pair of half arrows: one pointing up and the other down. For the element N, the electron configuration is 1 s superscript 2 2 s superscript 2 2 p superscript 3. Each of the squares in the group of 3 contains a single upward pointing arrow for this element. For the element O, the electron configuration is 1 s superscript 2 2 s superscript 2 2 p superscript 4. The first square in the group of 3 contains a pair of arrows and the last two squares contain single upward pointing arrows. For the element F, the electron configuration is 1 s superscript 2 2 s superscript 2 2 p superscript 5. The first two squares in the group of 3 each contain a pair of arrows and the last square contains a single upward pointing arrow. For the element N e, the electron configuration is 1 s superscript 2 2 s superscript 2 2 p superscript 6. The squares in the group of 3 each contains a pair of arrows.

The alkali metal sodium (atomic number 11) has one more electron than the neon atom. This electron must go into the lowest-energy subshell available, the 3s orbital, giving a 1s22s22p63s1 configuration. We can abbreviate electron configurations by writing the a noble gas configuration, which consists of the elemental symbol of the last noble gas prior to that atom, followed by the configuration of the remaining electrons. For our sodium example, the noble gas (or abbreviated or condensed) configuration is [Ne]3s1.

When we come to the alkali metal potassium (atomic number 19), we might expect that we would begin to add electrons to the 3d subshell. However, all available chemical and physical evidence indicates that potassium is like lithium and sodium, and that the next electron is not added to the 3d level but is, instead, added to the 4s level. As discussed previously, the 3d orbital with no radial nodes is higher in energy because it is less penetrating and more shielded from the nucleus than the 4s, which has three radial nodes. Thus, potassium has an electron configuration of [Ar]4s1.

Beginning with the transition metal scandium (atomic number 21), additional electrons are added successively to the 3d subshell. This subshell is filled to its capacity with 10 electrons (remember that for l = 2 [d orbitals], there are 2l + 1 = 5 values of ml, meaning that there are five d orbitals that have a combined capacity of 10 electrons). The 4p subshell fills next. Note that for three series of elements, scandium (Sc) through copper (Cu), yttrium (Y) through silver (Ag), and lutetium (Lu) through gold (Au), a total of 10 d electrons are successively added to the (n – 1) shell next to the n shell to bring that (n – 1) shell from 8 to 18 electrons. For two series, lanthanum (La) through lutetium (Lu) and actinium (Ac) through lawrencium (Lr), 14 f electrons (l = 3, 2l + 1 = 7 ml values; thus, seven orbitals with a combined capacity of 14 electrons) are successively added to the (n – 2) shell to bring that shell from 18 electrons to a total of 32 electrons.

Example 2: Quantum Numbers and Electron Configurations

What is the electron configuration and orbital diagram for a phosphorus atom? What are the four quantum numbers for the last electron added?

Solution

The atomic number of phosphorus is 15. Thus, a phosphorus atom contains 15 electrons. The order of filling of the energy levels is 1s, 2s, 2p, 3s, 3p, 4s, . . . The 15 electrons of the phosphorus atom will fill up to the 3p orbital, which will contain three electrons:

This figure provides the electron configuration 1 s superscript 2 2 s superscript 2 2 p superscript 6 3 s superscript 2 3 p superscript 3. It includes a diagram with two individual squares followed by 3 connected squares, a single square, and another connected group of 3 squares all in a single row. The first square is labeled below as, “1 s.” The second is similarly labeled, “2 s.” The first group of connected squares is labeled below as, “2 p.” The square that follows is labeled, “3 s,” and the final group of three squares is labeled, “3 p.” All squares except the last group of three squares has a pair of half arrows: one pointing up and the other down. Each of the squares in the last group of 3 contains a single upward pointing arrow.

The last electron added is a 3p electron. Therefore, n = 3 and, for a p-type orbital, l = 1. The ml value could be –1, 0, or +1. The three p orbitals are degenerate, so any of these ml values is correct. For unpaired electrons, convention assigns the value of +½ for the spin quantum number; thus, ms = +½.

Check Your Learning

Identify the atoms from the electron configurations given:

  1. [Ar]4s23d5
  2. [Kr]5s24d105p6

Answer

(a) Mn;  (b) Xe

Electron Configuration Exceptions

The periodic table can be a powerful tool in predicting the electron configuration of an element. However, we do find exceptions to the order of filling of orbitals shown in Figure 6. For instance, the ground state electron configuration of the transition metal chromium (Cr; atomic number 24) is [Ar]4s13d5 and that of copper (Cu; atomic number 29) is [Ar]4s13d10. In general, such exceptions involve subshells with very similar energy, and small effects can lead to changes in the order of filling.

In the case of Cr and Cu, we find that half-filled and completely filled subshells apparently represent conditions of preferred stability. This stability is such that an electron shifts from the 4s into the 3d orbital to gain the extra stability of a half-filled 3d subshell (in Cr) or a filled 3d subshell (in Cu). Other exceptions also occur. For example, niobium (Nb, atomic number 41) is predicted to have the electron configuration [Kr]5s24d3. Experimentally, we observe that its ground-state electron configuration is actually [Kr]5s14d4. We can rationalize this observation by saying that the electron–electron repulsions experienced by pairing the electrons in the 5s orbital are larger than the gap in energy between the 5s and 4d orbitals. There is no simple method to predict the exceptions for atoms where the magnitude of the repulsions between electrons is greater than the small differences in energy between subshells.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103 Resource Book Copyright © by Chem 103 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book