Pressure and Ideal Gas Law

Chem 103 Textbook Team

Pressure and Ideal Gas Law

Pressure and Atmospheric Pressure

The earth’s atmosphere exerts a pressure, as does any other gas. Although we do not normally notice atmospheric pressure, we are sensitive to pressure changes—for example, when your ears “pop” during take-off and landing while flying, or when you dive underwater. Gas pressure is caused by the force exerted by gas molecules colliding with the surfaces of objects. Although the force of each collision is very small, any surface of appreciable area experiences a large number of collisions in a short time, which can result in a high pressure. In fact, normal air pressure is strong enough to crush a metal container when not balanced by equal pressure from inside the container.

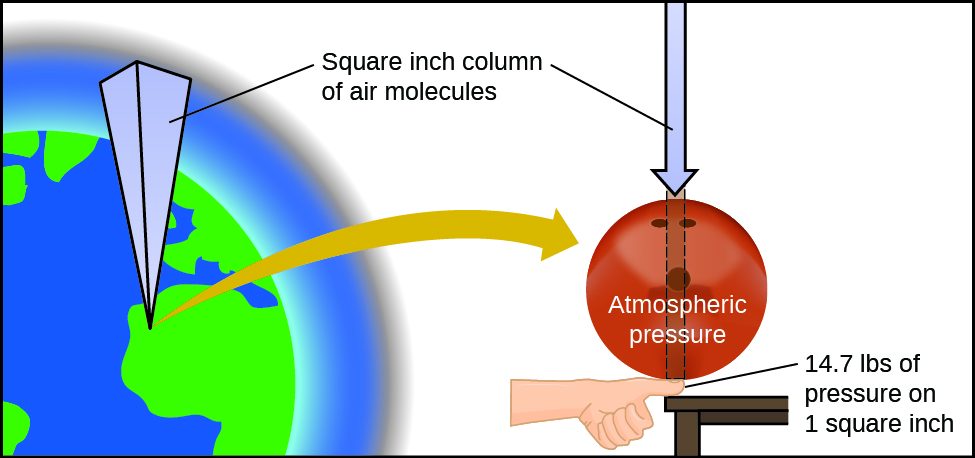
The left side of this figure includes a graphic of the earth with an inverted rectangular prism extending from a point on it. Near the top of the image, the label, “square inch column of air molecules” is connected to the prism with a line segment. This label is also connected with a line segment to a downward pointing arrow at the right side of the figure. Beneath the arrow is a red circle labeled, “atmospheric pressure.” A narrow rectangle with a dashed line border extends from the bottom of the arrow vertically through the circle. Directly beneath this rectangle at the lower edge of the circle is a hand with a thumb appearing to be resting on a tabletop. The thumb is connected with a line segment to the label, “14.7 lbs of pressure on 1 square inch.” The red circle is sitting on top of the thumb. — **Figure 1**. The atmosphere above us exerts a large pressure on objects at the surface of the earth, roughly equal to the weight of a bowling ball pressing on an area the size of a human thumbnail.

Atmospheric pressure is caused by the weight of the column of air molecules in the atmosphere above an object. At sea level, this pressure is roughly the same as that exerted by a full-grown African elephant standing on a doormat, or a typical bowling ball resting on your thumbnail. These may seem like huge amounts, and they are, but life on earth has evolved under such atmospheric pressure. If you actually perch a bowling ball on your thumbnail, the pressure experienced is twice the usual pressure, and the sensation is unpleasant.

Demonstration: Effect of atmospheric pressure

Set up. The effect of atmospheric pressure can be seen in the following two videos. In the first video, you will see the effect of atmospheric pressure on a soda can. Before the video was recorded, a small amount of water was put into the soda can and then boiled. After boiling the water for a while, the video begins. You can see the water vapor (steam) coming out of the can at the beginning of the video. Then the can is inverted in a cold water bath.

Explanation. The can was crushed by the atmospheric pressure. Usually, a can is not susceptible to the atmospheric pressure in this way because the pressure inside the open can is equal to the pressure outside the open can. But when the can was heated and the water inside was boiled, the vapor from the boiling water pushed air out of the can. After suddenly cooling the water vapor inside the can by inverting it into a cold water bath, the water vapor condensed and a partial vacuum was formed. The atmospheric pressure outside the can was greater than the pressure inside the can, and the can was crushed because the aluminum could not withstand the atmospheric pressure.

In the next video, the experiment is scaled up considerably and performed on a tanker. In this video, instead of heating the tanker car to drive out the air, a vacuum pump was used to pump out the air molecules. Before this particular part of the video, the team pumped air from the intact tanker car and the car did not collapse. Even though the atmospheric pressure outside the tanker car was greater than the pressure inside the tanker car, the walls of the tanker are strong enough to withstand this pressure difference (something the aluminum can above was not capable of). In this section of the video, the team disrupts the integrity of the structure by making a dent in the tanker before pulling a vacuum.

Explanation. You can see that the atmospheric pressure is even strong enough to crush a tanker car (provided the tanker car is already damaged in some way). This is the pressure that we are accustomed to living under every day, but these videos demonstrate how much pressure this really is.

In general, pressure is defined as the force exerted on a given area: P = $\dfrac{\text{F}}{\text{A}}$ . The SI unit of pressure is the pascal (Pa), with 1 Pa = 1 N/m², where N is a newton, a unit of force defined as 1 kg·m/s². One pascal is a small pressure which is why it is more convenient to use units of kilopascal (1 kPa = 1000 Pa) or bar (1 bar = 100,000 Pa). In the United States, pressure is often measured in pounds of force on an area of one square inch—pounds per square inch (psi)—for example, in car tires. Pressure can also be measured using the unit atmosphere (atm), which originally represented the average sea level air pressure at the approximate latitude of Paris (45°).

Ideal Gas Law

An ideal gas consists of particles (atoms or molecules) that have the following properties:

Particles have no volume.
They are very small compared to the size of the container and compared to the distance between them.
Particles exert no forces on each other.
Particles are neither attracted to, nor repelled from, each other.
Particles are in constant motion.
They undergo billiard-ball-like collisions with the walls of the container and with each other.

The ideal gas law describes the relation between the pressure, volume, temperature, and number of moles of a gas:

PV = nRT

In this equation, P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure and volume will determine the proper form of the gas constant as required by dimensional analysis, the most commonly encountered values is 0.08206 L atm mol^–1 K^–1 (hence, P is in atm and V is in L).

The ideal gas equation contains four variables, P, V, n, and T, and the gas constant R. Typically any three of these variables will permit use of the ideal gas law to calculate the fourth variable as demonstrated in the following example exercises.

Example 1

Methane, CH₄, is being considered for use as an alternative automotive fuel to replace gasoline. One gallon of gasoline could be replaced by 655 g of CH₄. What is the volume of this much methane at 25 °C and 745 torr?

Solution

We must rearrange PV = nRT to solve for V:

V = $\dfrac{n\text{RT}}{\text{P}}$

If we use R = 0.08206 L atm mol^–1 K^–1, then the amount must be in moles, temperature must be in kelvin, and pressure must be in atm.

Converting into the “right” units:

n = 655 g CH₄ × $\dfrac{1 \;\text{mol}}{16.043 \;\rule[0.5ex]{2.6em}{0.1ex}\hspace{-2.6em}\text{g CH}_4}$ = 40.8 mol

T = 25 °C + 273 = 298 K

P = 745 ~~torr~~ × $\dfrac{1 \;\text{atm}}{760 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.8em}\text{torr}}$ = 0.980 atm

V = $\dfrac{n\text{RT}}{\text{P}} = \dfrac{(40.8 \;\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol})\left(0.08206 \frac{\text{L}\cdot\rule[0.3ex]{1.35em}{0.1ex}\hspace{-1.35em}\text{atm}}{\rule[0.3ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mol}\cdot\rule[0.4ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{K}}\right)(298 \;\rule[0.6ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K})}{0.980 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.8em}\text{atm}}$ = 1.02 × 10³ L

It would require 1020 L (269 gal) of gaseous methane at about 1 atm of pressure to replace 1 gal of gasoline. It requires a large container to hold enough methane at 1 atm to replace several gallons of gasoline.

Check Your Learning

Calculate the pressure of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.

Answer

345 atm

If the number of moles of an ideal gas are kept constant under two different sets of conditions, a useful mathematical relationship called the combined gas law is obtained: $\dfrac{\text{P}_{1}\text{V}_{1}}{\text{T}_{1}} = \dfrac{\text{P}_{2}\text{V}_{2}}{\text{T}_{2}}$ using units of atm, L, and K. Both sets of conditions are equal to the product of n × R (where n = the number of moles of the gas and R is the ideal gas law constant).

Example 2

When filled with air, a typical scuba tank with a volume of 13.2 L has a pressure of 153 atm. If the water temperature is 27 °C, how many liters of air will such a tank provide to a diver’s lungs at a depth of approximately 70 feet in the ocean where the pressure is 3.13 atm?

Solution

Letting 1 represent the air in the scuba tank and 2 represent the air in the lungs, and noting that body temperature (the temperature the air will be in the lungs) is 37 °C, we have:

$\dfrac{\text{P}_{1}\text{V}_{1}}{\text{T}_{1}} = \dfrac{\text{P}_{2}\text{V}_{2}}{\text{T}_{2}} \;\;\longrightarrow\;\; \dfrac{(153 \;\text{atm})(13.2 \;\text{L})}{(300 \;\text{K})} = \dfrac{(3.13 \;\text{atm})(V_2)}{(310 \;\text{K})}$

Solving for V₂:

V₂ = $\dfrac{(153 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.7em}\text{atm})(13.2 \;\text{L})(310 \;\rule[0.6ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K})}{(300 \;\rule[0.6ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K})(3.13 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.7em}\text{atm})}$ = 667 L

(Note: Be advised that this particular example is one in which the assumption of ideal gas behavior is not very reasonable, since it involves gases at relatively high pressures and low temperatures. Despite this limitation, the calculated volume can be viewed as a good “ballpark” estimate.)

Check Your Learning

A sample of ammonia is found to occupy 0.250 L under laboratory conditions of 27 °C and 0.850 atm. Find the volume of this sample at 0 °C and 1.00 atm.

Answer

0.193 L

Chemistry in Real Life: The Interdependence between Ocean Depth and Pressure in Scuba Diving

Whether scuba diving at the Great Barrier Reef in Australia or in the Caribbean, divers must understand how pressure affects a number of issues related to their comfort and safety.

The pressure a diver experiences is the sum of all pressures above the diver (from the water and the air) and therefore increases with depth. Most pressure measurements are given in units of atmospheres, expressed as “atmospheres absolute” or ATA in the diving community: Every 33 feet of salt water represents 1 ATA of pressure in addition to 1 ATA of pressure from the atmosphere at sea level. As a diver descends, the increase in pressure causes the body’s air pockets in the ears and lungs to compress; on the ascent, the decrease in pressure causes these air pockets to expand, potentially rupturing eardrums or bursting the lungs. Divers must therefore undergo equalization by adding air to body airspaces on the descent by breathing normally and adding air to the mask by breathing out of the nose or adding air to the ears and sinuses by equalization techniques; the corollary is also true on ascent, divers must release air from the body to maintain equalization. Buoyancy, or the ability to control whether a diver sinks or floats, is controlled by the buoyancy compensator (BCD). If a diver is ascending, the air in his BCD expands because of lower pressure according to Boyle’s law (decreasing the pressure of gases increases the volume). The expanding air increases the buoyancy of the diver, and she or he begins to ascend. The diver must vent air from the BCD or risk an uncontrolled ascent that could rupture the lungs. In descending, the increased pressure causes the air in the BCD to compress and the diver sinks much more quickly; the diver must add air to the BCD or risk an uncontrolled descent, facing much higher pressures near the ocean floor. The pressure also impacts how long a diver can stay underwater before ascending. The deeper a diver dives, the more compressed the air that is breathed because of increased pressure: If a diver dives 33 feet, the pressure is 2 ATA and the air would be compressed to one-half of its original volume. The diver uses up available air twice as fast as at the surface.

Kinetic Molecular Theory of Gases

Kinetic molecular theory (KMT) is a simple microscopic model that effectively explains the ideal gas law described above. This theory is based on the following postulates, which you have seen before in our definition of an ideal gas:

Gases consist of tiny particles that move at different speeds and in every possible direction; they are in constant motion.
The size of gas particles is much smaller than the distances between them. Most of the volume of a gas is empty space.
There is no force of attraction or repulsion between gas particles. This is because the molecules are so far apart from each other.
They undergo billiard-ball-like collisions (elastic collisions) with the walls of the container and with each other.

The various pressure, temperature, and volume relationships of an ideal gas can be derived from the assumptions of the KMT. Recall that gas pressure is exerted by rapidly moving gas molecules and depends directly on the number of molecules hitting a unit area of the wall per unit of time, we see that the KMT conceptually explains the behavior of a gas as follows:

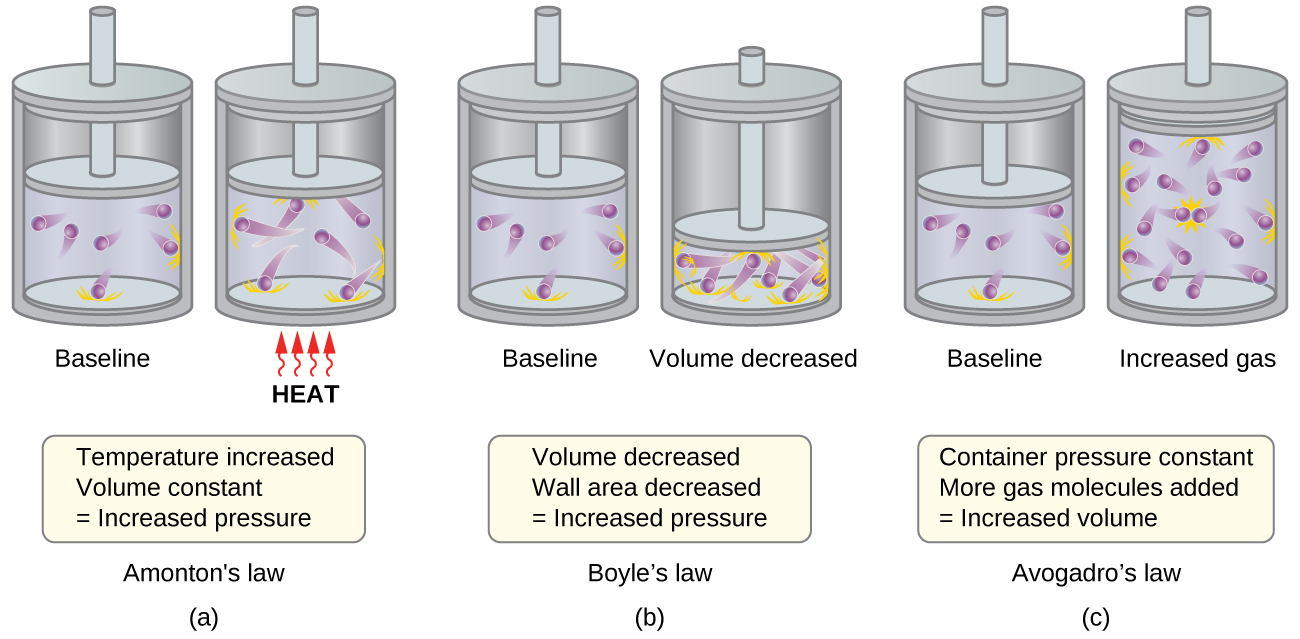
This figure shows 3 pairs of pistons and cylinders. In a, which is labeled, “Charles’s Law,” the piston is positioned for the first cylinder so that just over half of the available volume contains 6 purple spheres with trails behind them. The trails indicate movement. Orange dashes extend from the interior surface of the cylinder where the spheres have collided. This cylinder is labeled, “Baseline.” In the second cylinder, the piston is in the same position, and the label, “Heat” is indicated in red capitalized text. Four red arrows with wavy stems are pointing upward to the base of the cylinder. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. A rectangle beneath the diagram states, “Temperature increased, Volume constant equals Increased pressure.” In b, which is labeled, “Boyle’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the piston has been moved, decreasing the volume available to the 6 purple spheres to half of the initial volume. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. This second cylinder is labeled, “Volume decreased.” A rectangle beneath the diagram states, “Volume decreased, Wall area decreased equals Increased pressure.” In c, which is labeled “Avogadro’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the number of purple spheres has changed from 6 to 12 and volume has doubled. This second cylinder is labeled “Increased gas.” A rectangle beneath the diagram states, “At constant pressure, More gas molecules added equals Increased volume.” — **Figure 1**. (a) When gas temperature increases, gas pressure increases due to increased force and frequency of molecular collisions. (b) When volume decreases, gas pressure increases due to increased frequency of molecular collisions. (c) When the amount of gas increases at a constant pressure, volume increases to yield a constant number of collisions per unit wall area per unit time.

Figure 1a: Relationship between Pressure and Temperature (also known as Amonton or Gay-Lussac’s Law, P ∝ T; when V, n are constant)
- If the temperature is increased, the average speed and kinetic energy of the gas molecules increase. If the volume is held constant, the increased speed of the gas molecules results in more frequent and more forceful collisions with the walls of the container, therefore increasing the pressure.
Relationship between Volume and Temperature (also known as Charles’s Law, V ∝ T; when P, n are constant)
- If the temperature of a gas is increased, a constant pressure may be maintained only if the volume occupied by the gas increases. This will result in greater average distances traveled by the molecules to reach the container walls. One example is a cylinder like that shown in Figure 1 with a piston that moves to increase the volume. These conditions will decrease the frequency of molecule-wall collisions.
Figure 1b: Relationship between Volume and Pressure (also known as Boyle’s Law, P ∝ 1/V; when T, n are constant)
- If the gas volume is decreased, the distance to the container walls decreases, and the frequency of collisions with the wall increases, thereby increasing the pressure.
Figure 1c: Relation between Volume and Mole Number (also known as Avogadro’s Law, V ∝ n; when T, P are constant)
- At fixed pressure and temperature. The more molecules, the more volume.
Relation between Pressure and Number of Different Molecules (Dalton’s Law, P_total = P₁ + P₂ + P₃ …)
- Because of the large distances between them, the molecules of one gas in a mixture bombard the container walls with the same frequency whether other gases are present or not, and the total pressure of a gas mixture equals the sum of the (partial) pressures of the individual gases.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License