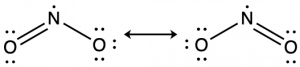
Resonance Structures and Formal Charge
Covalent Bond Length and Strength
Stable molecules exist because covalent bonds hold the atoms together. We measure the strength of a covalent bond by the energy required to break it, that is, the energy necessary to separate the bonded atoms. Separating any pair of bonded atoms requires energy. The stronger a bond, the greater the energy required to break it.
The energy required to break a specific covalent bond in one mole of gaseous molecules is called the bond energy or the bond dissociation energy. The bond energy for a diatomic molecule is defined as the standard enthalpy change for the endothermic reaction:
XY(g) → X(g) + Y(g) ΔH°
For example, the bond energy of the pure covalent H–H bond is 436 kJ per mole of H–H bonds broken:
H2(g) → 2 H(g) ΔH° = 436 kJ/mol
Molecules with three or more atoms have two or more bonds. The sum of all bond energies in such a molecule is equal to the standard enthalpy change for the endothermic reaction that breaks all the bonds in the molecule. For example, the sum of the four C–H bond energies in CH4, 1664 kJ/mol, is equal to the standard enthalpy change of the reaction:
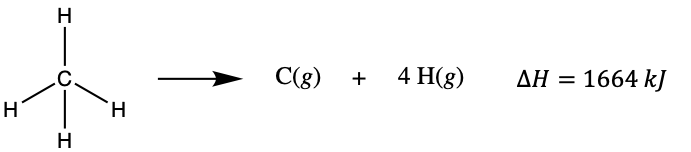
The average C–H bond energy is 1664/4 = 416 kJ/mol because there are four moles of C–H bonds broken per mole of the reaction. Although the four C–H bonds are equivalent in the original molecule, they do not each require the same energy to break; once the first bond is broken (which requires >450 kJ/mol), the remaining bonds are easier to break. The average C-H bond energy is not only averaged over each C-H bond broken within a single molecule, but the average of C-H bond energies of many molecules. For example, ethane, C2H6, has an actual C-H bond energy closer to 423 kJ/mol. The 416 kJ/mol value is the average, not the exact value required to break any one bond in any one molecule.
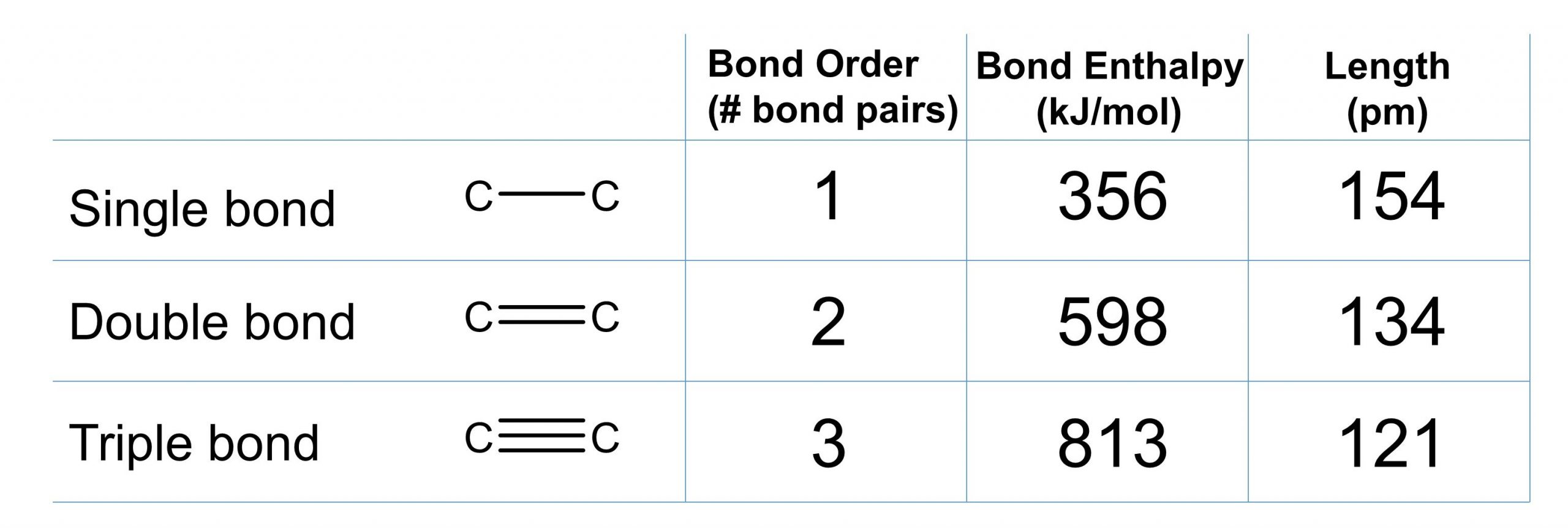
The strength of a bond between two atoms increases as the number of electron pairs in the bond increases. Generally, as the bond strength increases, the bond length decreases. Thus, we find that triple bonds are stronger and shorter than double bonds between the same two atoms; likewise, double bonds are stronger and shorter than single bonds between the same two atoms. The average bond energies for some common bonds are listed below:
Average Bond Enthalpy
In kJ/mol
| I | Br | Cl | S | P | Si | F | O | N | C | H | |
| H | 299 | 366 | 431 | 347 | 322 | 323 | 566 | 467 | 391 | 416 | 436 |
| C | 213 | 285 | 327 | 272 | 264 | 301 | 485 | 358 | 285 | 346 | |
| N | - | - | 193 | - | ~200 | 335 | 272 | 201 | 160 | ||
| O | 201 | - | 205 | - | ~340 | 368 | 190 | 146 | |||
| F | - | 238 | 255 | 326 | 490 | 582 | 158 | ||||
| Si | 234 | 310 | 391 | 226 | - | 226 | |||||
| P | 184 | 264 | 319 | - | 209 | ||||||
| S | - | 213 | 255 | 226 | Multiple Bonds | Multiple Bonds | |||||
| Cl | 209 | 217 | 242 | N=N | 418 | C=C | 598 | ||||
| Br | 180 | 193 | N≡N | 946 | C≡C | 813 | |||||
| I | 151 | C=N | 616 | C=O in CO2 | 803 | ||||||
| C≡N | 866 | C=O carbonyl | 695 | ||||||||
| N=O | 607 | C≡O | 1073 | ||||||||
| O=O in O2 | 498 | N≡O | 632 | ||||||||
| Data from Cotton, F.A., Wilkinson, G. and Gaus, P.L., Basic Inorganic Chemistry, 3rd ed., New York: Wiley, 1995. Corrected values for C-C and C-O from Cottrell, T.L., The Strengths of Chemical Bonds, 2ed., London:Butterworths, 1958. |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
The average bond lengths for some common bonds are listed below:
Average Bond Length
In picometers, (pm)
| I | Br | Cl | S | P | Si | F | O | N | C | H | |
| H | 161 | 142 | 127 | 132 | 138 | 145 | 92 | 94 | 98 | 110 | 74 |
| C | 210 | 191 | 176 | 181 | 187 | 194 | 141 | 143 | 147 | 154 | |
| N | 203 | 184 | 169 | 174 | 180 | 187 | 134 | 136 | 140 | ||
| O | 199 | 180 | 165 | 170 | 176 | 183 | 130 | 148 | |||
| F | 197 | 178 | 163 | 168 | 174 | 181 | 141 | ||||
| Si | 250 | 231 | 216 | 221 | 227 | 234 | |||||
| P | 243 | 224 | 209 | 214 | 220 | ||||||
| S | 237 | 218 | 203 | 208 | Multiple Bonds | Multiple Bonds | |||||
| Cl | 232 | 213 | 200 | N=N | 120 | C=C | 134 | ||||
| Br | 247 | 228 | N≡N | 110 | C≡C | 121 | |||||
| I | 266 | C=N | 127 | C=O in CO2 | 116 | ||||||
| C≡N | 115 | C=O carbonyl | 121 | ||||||||
| N=O | 118 | C≡O | 113 | ||||||||
| O=O in O2 | 121 | N≡O | 108 | ||||||||
Comparisons of these average bond energy and length values show that when one atom bonds to various atoms in a group, the bond strength typically decreases (and bond length increases) as we move down the group. For example, C–F is 485 kJ/mol and 141 pm, C–Cl is 327 kJ/mol and 176 pm, and C–Br is 285 kJ/mol and 191 pm.
Bond Order, Bond Length, and Bond Strength
The way that two nuclei share electrons in a bond affects quantities such as bond order, bond polarity, bond length, and bond strength. Bond order is the number of electron-pair bonds connecting two nuclei. The Lewis structure of formaldehyde, CH2O, that contributes the most to the bonding in the molecule is as shown.
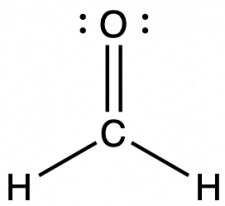 Looking at the structure of formaldehyde we can see that there is a double bond between the central carbon atom and the oxygen atom giving a CO bond order of two. The carbon is singly bonded to each hydrogen atom, which would give each CH bond orders of one.
Looking at the structure of formaldehyde we can see that there is a double bond between the central carbon atom and the oxygen atom giving a CO bond order of two. The carbon is singly bonded to each hydrogen atom, which would give each CH bond orders of one.
Bond order is an index of bond strength: the higher the bond order, the stronger the bond. Bond strength is a measured quantity: the energy (in kJ/mol) required to break a chemical bond, tabulated above. The stronger the bond, the more energy that is required to break the bond. This means that a C=O double bond is stronger than a C-O single bond, and the C=O double bond requires more energy to break than a C-O single bond. Bond length is the equilibrium distance between two nuclei. Higher bond orders generally correlate with shorter bond distances. The C=O double bond is shorter than the C-O single bond.
We can apply these same concepts to carbon-carbon single, double, and triple bonds to compare how bond order, bond length and bond strength are related (Figure 1).
Resonance Structures
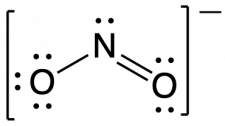 Following the five steps for drawing a Lewis structure we can determine a valid Lewis structure for NO2–:
Following the five steps for drawing a Lewis structure we can determine a valid Lewis structure for NO2–:
If this representation is the only correct resonance structure, we would expect the molecule to be asymmetric, meaning the bond lengths between the central nitrogen and the oxygen atoms would be different. A double bond between two atoms is shorter (and stronger) than a single bond between the same two atoms. As we will see from the discussion of formal charge below, we would also expect that the electrons would be distributed such that the negative charge would be present on one oxygen atom. Experimental evidence, however, establishes that nitrite is symmetric and that both N–O bonds in NO2− have the same strength and length. The two N-O bonds and the two oxygen atoms in nitrite are equivalent in all chemical and physical properties.
It is not possible to write a single Lewis structure for NO2− which accurately represents the electronic structure. Instead, we use the concept of resonance: if two or more Lewis structures with the same arrangement of atoms can be written for a molecule or ion, the actual distribution of electrons is a weighted average of the valid Lewis structures.
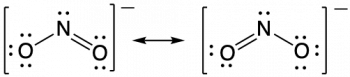 Therefore, two valid Lewis structures must be drawn to represent the bonding in the nitrite ion, NO2–. The two headed arrow that connects two (or more) valid Lewis structures is important. It communicates that we’re talking about resonance structures and not a chemical reaction (which is signified by a single-headed arrow, →) or equilibrium (which is signified by two arrows, ⇌).
Therefore, two valid Lewis structures must be drawn to represent the bonding in the nitrite ion, NO2–. The two headed arrow that connects two (or more) valid Lewis structures is important. It communicates that we’re talking about resonance structures and not a chemical reaction (which is signified by a single-headed arrow, →) or equilibrium (which is signified by two arrows, ⇌).
The nitrite ion is an example of equivalent resonance, which means that the two bonds are identical. Both NO bonds have the same atoms involved, the same length, and require the same energy added to break them. Thus, the two NO bonds are identical. The actual distribution of electrons in each of the NO bonds in NO2− is the weighted average of a double bond and a single bond. Since the bonds are equivalent, they are equally weighted, so each connection between nitrogen and oxygen has an N-O bond order of 1.5.
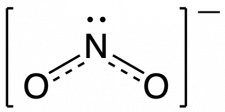 The actual electronic structure of the molecule (the weighted average of the resonance forms) is represented by a resonance hybrid of the individual resonance forms, as shown.
The actual electronic structure of the molecule (the weighted average of the resonance forms) is represented by a resonance hybrid of the individual resonance forms, as shown.
We should remember that a molecule described as a resonance hybrid never possesses an electronic structure described by either resonance form. It does not fluctuate between resonance forms; rather, the actual electronic structure is always the weighted average of that shown by all resonance forms.
Notice that the atoms did not change position in the nitrite example of resonance. If atom positions change with respect to one another, then this is not an example of resonance. Instead, the molecules are isomers involved in a chemical change, and that will be explored in future courses.
The carbonate anion, CO32−, provides a second example of a polyatomic ion with equivalent resonance or equally weighted resonance structures:
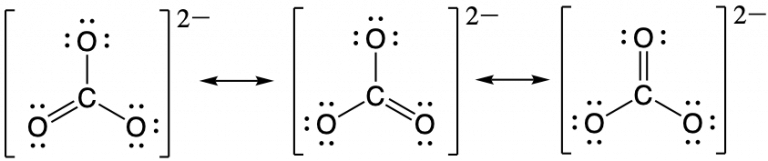
One oxygen atom must have a double bond to carbon to complete the octet on the central atom. All oxygen atoms, however, are equivalent, and the Lewis structure could be drawn with the double bond between carbon and any one of the three oxygen atoms. This gives rise to three equivalent resonance forms of the carbonate ion. Because we can write three equivalent resonance structures, we know that the actual arrangement of electrons in the carbonate ion is the equally weighted average of the three structures. These three structures highlight the symmetric bonding and distribution of electrons present in the carbonate ion. Again, experimental evidence establishes the symmetry of carbonate and shows that all three CO bonds are equivalent (bond length and bond strength) and that each oxygen atom is chemically equivalent.
Bond Order Revisited
As we described at the beginning of this section, bond order is the number of electron-pair bonds connecting two atoms. Using the carbonate ion, CO32- as an example, we already know the possible resonance structures for this ion. If we would like to determine the bond order between the central carbon and the top oxygen atom (labeled with a number one in the image below), we can calculate that CO bond order in each resonance structure and then divide by the total number of resonance structures.
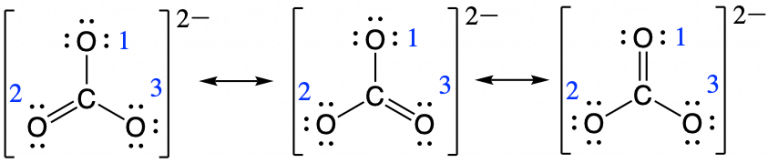
So for determining the bond order between carbon and oxygen number one the calculation would be as follows:
bond order for oxygen one = ![]()
and for oxygen number two:
bond order for oxygen two = ![]()
and for oxygen number three:
bond order for oxygen three = ![]()
 This gives the bond order between the central carbon and each oxygen atom as being 4/3. This means that in the resonance hybrid each bond between carbon and oxygen has bond character that is between that of a single bond and a double bond, which we have proven experimentally.
This gives the bond order between the central carbon and each oxygen atom as being 4/3. This means that in the resonance hybrid each bond between carbon and oxygen has bond character that is between that of a single bond and a double bond, which we have proven experimentally.
As indicated by the resonance hybrid and the bond order calculation, each bond between carbon and oxygen has a total bond order between that of a single bond (bond order = 1) and a double bond (bond order = 2). This is consistent with all of the experimental observations of the bond lengths and the reactivity of each atom, as well as theoretical predictions of the electronic structure.
All of the resonance structures we’ve considered up to this point have been equivalent to one another. That is, the location of the double bond had an equal likelihood of being associated with any of the oxygen atoms in NO2– or CO32- so each resonance structure has equal stability. There are molecules where one resonance structure may not be as stable as another while still satisfying the octet rule. We are able to compare these resonance structures to one another using a concept known as formal charge.
Formal Charge
The formal charge of an atom in a molecule is the hypothetical charge the atom would have if we could redistribute the electrons in the bonds evenly between the atoms. Another way of saying this is that formal charge results when we take the number of valence electrons of a neutral atom, subtract the nonbonding electrons, and then subtract half the number of bonding electrons (distribute them evenly to each of the two atoms that are bonded).
Thus, we calculate formal charge as: 
By subtracting one-half the number of bonding electrons, we essentially assign half the bonding electrons to each atom. This implicitly assumes that these bonding electrons are shared relatively equally, as in covalent bonding. Since each bond represents two electrons, we can also count the number of bonds connected to that atom in the Lewis structure and the equation becomes:

The previous two equations are both common ways of calculating formal charge and will yield the same answer. The sum of the formal charges on all atoms in a neutral molecule is zero; the sum of the formal charges on a polyatomic ion is the charge on the ion.
We must remember that the formal charge calculated for an atom is not the actual charge of the atom in the molecule. Formal charge is only a useful bookkeeping procedure; it does not indicate the presence of actual charges.
Example 1: Calculating Formal Charge from Lewis Structures
Assign formal charges to each atom in the interhalogen ion ICl4−.
Solution
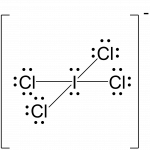 We divide the bonding electron pairs equally for all I–Cl bonds:
We divide the bonding electron pairs equally for all I–Cl bonds:- We assign lone pairs of electrons to their atoms. Each Cl atom now has 6 unshared electrons and 2 bonding electrons, and the I atom has 4 unshared electrons and 8 bonding electrons.
- Subtract the number of unshared electrons + ½ number of bonding electrons from the number of valence electrons for the neutral atom:
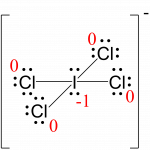 I: 7 – (4 + ½ (8)) = –1
I: 7 – (4 + ½ (8)) = –1
Cl: 7 – (6 + ½ (2)) = 0The sum of the formal charges of all the atoms equals –1, which is identical to the charge of the ion (–1).
The formal charges for each atom are drawn next to them in red for the final Lewis structure.
Check Your Learning
![]() Calculate the formal charge for each atom in the carbon monoxide molecule.
Calculate the formal charge for each atom in the carbon monoxide molecule.
Answer
C −1, O +1. ![]()
Example 2: Calculating Formal Charge from Lewis Structures
Assign formal charges to each atom in the interhalogen molecule BrCl3.
Solution
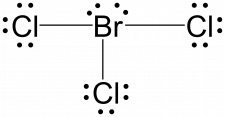 Assign one of the electrons in each Br–Cl bond to the Br atom and one to the Cl atom in that bond:
Assign one of the electrons in each Br–Cl bond to the Br atom and one to the Cl atom in that bond:- Assign the lone pairs to their atom. Now each Cl atom has 6 unshared electrons and 2 bonding electrons, and the Br atom has 4 unshared electrons and 6 bonding electrons.
- Subtract this number from the number of valence electrons for the neutral atom. This gives the formal charge:
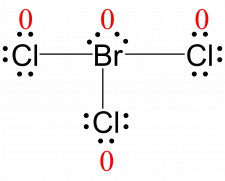 Br: 7 – (4 + ½ (6)) = 0
Br: 7 – (4 + ½ (6)) = 0
Cl: 7 – (6 + ½ (2)) = 0All atoms in BrCl3 have a formal charge of zero, and the sum of the formal charges totals zero, as it must in a neutral molecule.
The formal charges for each atom are drawn next to them in red for the final Lewis structure.
Check Your Learning
Determine the formal charge for each atom in NCl3.
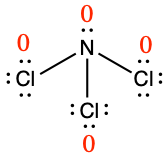
Answer
N: 0; all three Cl atoms: 0
Using Formal Charge to Predict Resonance Structure Contributions
As discussed previously, molecules often have more than one valid Lewis structure. These resonance structures contribute to the overall resonance hybrid for a given molecule. However, not all resonance structures contribute equally to the bonding of a molecule. The most stable individual resonance structure (and thus the largest contributor to the resonance hybrid) tends to:
- Minimize formal charges on atoms.
- Place negative formal charges on more electronegative atoms.
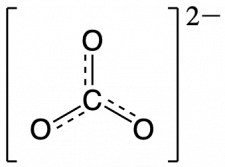
To see how these guidelines apply, let us consider some possible structures for carbon dioxide, CO2, with carbon as the central atom. We can draw three possibilities for the structure, and assigning formal charge to each atom gives us the following values:
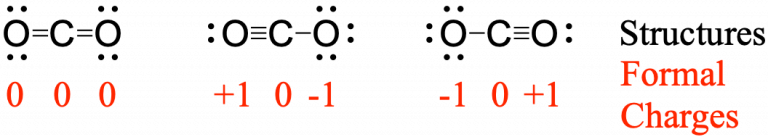
Computational chemistry predicts that the left structure (which minimizes formal charge since all atoms have a formal charge of zero) contributes the greatest to the bonding in CO2 (~50%). The other two structures contribute less to the bonding structure (~25% each). Thus, CO2 has non-equivalent resonance structures. Formal charges help us estimate the relative contributions by each resonance structure when non-equivalent resonance structures contribute to the resonance hybrid.
Example 3: Using Formal Charge to Determine Major Resonance Structure
Nitrous oxide, N2O, commonly known as laughing gas, is used as an anesthetic in minor surgeries, such as the routine extraction of wisdom teeth. Which structure is the major contributor to the resonance hybrid?
![]()
Solution
Determining formal charge yields the following:
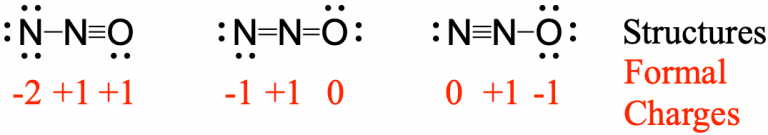
The structure in which the oxygen carries the negative formal charge ![]() is the major resonance contributor since oxygen is more electronegative than nitrogen. Additionally the number of atoms with formal charges are minimized since one atom has a formal charge of 0.
is the major resonance contributor since oxygen is more electronegative than nitrogen. Additionally the number of atoms with formal charges are minimized since one atom has a formal charge of 0.
Check Your Learning
Using formal charge, rationalize which structure contributes the most for the thiocyanate (SCN−) ion?
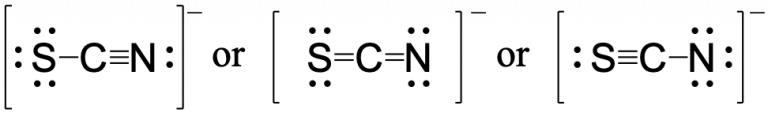
Answer
First, assign formal charges:
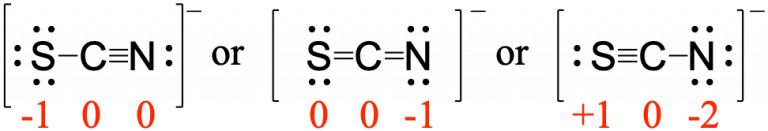
Major contributor is ![]()
In this resonance form of the thiocyanate ion, the formal charges are as follows:
S: 0; C: 0; N: -1
Since nitrogen is more electronegative than sulfur, placing the negative formal charge on nitrogen is favorable compared to the other two options above.
Valence Bond Theory and Resonance Structures
For molecules that have two or more major resonance structures, the hybridization and molecular geometry assigned to one resonance structure must be the same as all other resonance structures in the set. This is because a set of resonance structures describes a single molecule.
Hybridization involves only σ bonds, lone pairs of electrons, and single unpaired electrons (radicals). Structures that account for these features describe the correct hybridization of the atoms. However, many structures also include resonance forms. Remember that different resonance forms are required to represent the molecule when various arrangements of π bonds are possible.
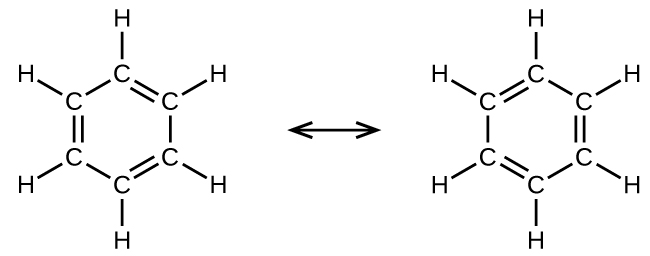 For example, the molecule benzene has two major resonance structures. We can use either of these structures to determine that each of the carbon atoms is bonded to three other atoms with no lone pairs, so the correct hybridization is sp2. The electrons in the unhybridized p orbitals form π bonds. Neither resonance structure completely describes the electrons in the π bonds. They are not located in one position or the other, but in reality are delocalized throughout the ring. A simple application of Valence Bond theory does not easily address delocalization. Bonding in molecules with resonance forms is better described by molecular orbital theory or by invoking hyperconjugation (to learn more, enroll in CHEM 343).
For example, the molecule benzene has two major resonance structures. We can use either of these structures to determine that each of the carbon atoms is bonded to three other atoms with no lone pairs, so the correct hybridization is sp2. The electrons in the unhybridized p orbitals form π bonds. Neither resonance structure completely describes the electrons in the π bonds. They are not located in one position or the other, but in reality are delocalized throughout the ring. A simple application of Valence Bond theory does not easily address delocalization. Bonding in molecules with resonance forms is better described by molecular orbital theory or by invoking hyperconjugation (to learn more, enroll in CHEM 343).
Example 4: Assignment of Hybridization Involving Resonance
Some acid rain results from the reaction of sulfur dioxide with atmospheric water vapor, followed by the formation of sulfuric acid. Sulfur dioxide, SO2, is a major component of volcanic gases as well as a product of the combustion of sulfur-containing coal. What is the hybridization of the S atom in SO2?
Solution
The resonance structures of SO2 are: 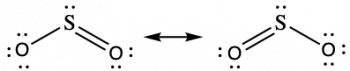
The sulfur atom is surrounded by two bonding regions and one lone pair of electrons in either resonance structure. Therefore, the electron-pair geometry is trigonal planar, and the hybridization of the sulfur atom is sp2.
Check Your Learning
Another acid in acid rain is nitric acid, HNO3, which is produced by the reaction of nitrogen dioxide, NO2, with atmospheric water vapor. What is the hybridization of the nitrogen atom in NO2? (Note: the lone electron on nitrogen occupies a hybridized orbital just as a lone pair would.)
Answer
sp2