Core and Valence Electrons

The electrons occupying the outermost shell orbital(s) are called valence electrons, and those occupying the inner shell orbitals are called core electrons (Figure 1). They can be more easily distinguished when using the noble gas configuration. For some examples, let us consider the ground state electron configurations of the elements in the 3rd period of the periodic table. For sodium, [Ne]3s¹, the symbol [Ne] represents core electrons (1s²2s²2p⁶) and the valence electron is the electron in the 3s orbital.

Compare this to the abbreviated configuration of lithium, [He]2s¹, where [He] represents the configuration of the helium atom, which is identical to that of the filled inner shell of lithium. And the abbreviated configuration of potassium, [Ar]4s¹, where [Ar] represents the configuration of the argon atom, which is identical to that of the filled inner shell of potassium.

Writing the configurations in this way emphasizes the similarity of the configurations of lithium, sodium and potassium. All three atoms, which are in the alkali metal family, have only one electron in a valence s subshell outside a filled set of inner shells.

Li: [He]2s¹
Na: [Ne]3s¹
K: [Ar]4s¹

The alkaline earth metal magnesium with its 12 electrons in a [Ne]3s² configuration, is analogous to its family members beryllium, [He]2s², and calcium, [Ar]4s². All three atoms have a filled s subshell outside their filled inner shells.

Aluminum (atomic number 13), with 13 electrons and the electron configuration [Ne]3s²3p¹, is analogous to its family member boron, [He]2s²2p¹. The electron configurations of silicon (14 electrons), phosphorus (15 electrons), sulfur (16 electrons), chlorine (17 electrons), and argon (18 electrons) are analogous in the electron configurations of their outer shells to their corresponding family members carbon, nitrogen, oxygen, fluorine, and neon, respectively, except that the principal quantum number of the outer shell of the heavier elements has increased by one to n = 3. Figure 2 shows the ground-state electron configuration for the outer-shell electrons of these elements as well as that for atoms of each of the known elements. (note that for p-block elements in periods 4-7, the outer-shell configurations in Figure 2 includes more than just the valence electrons; it also shows the full d and f subshells for clarity.)

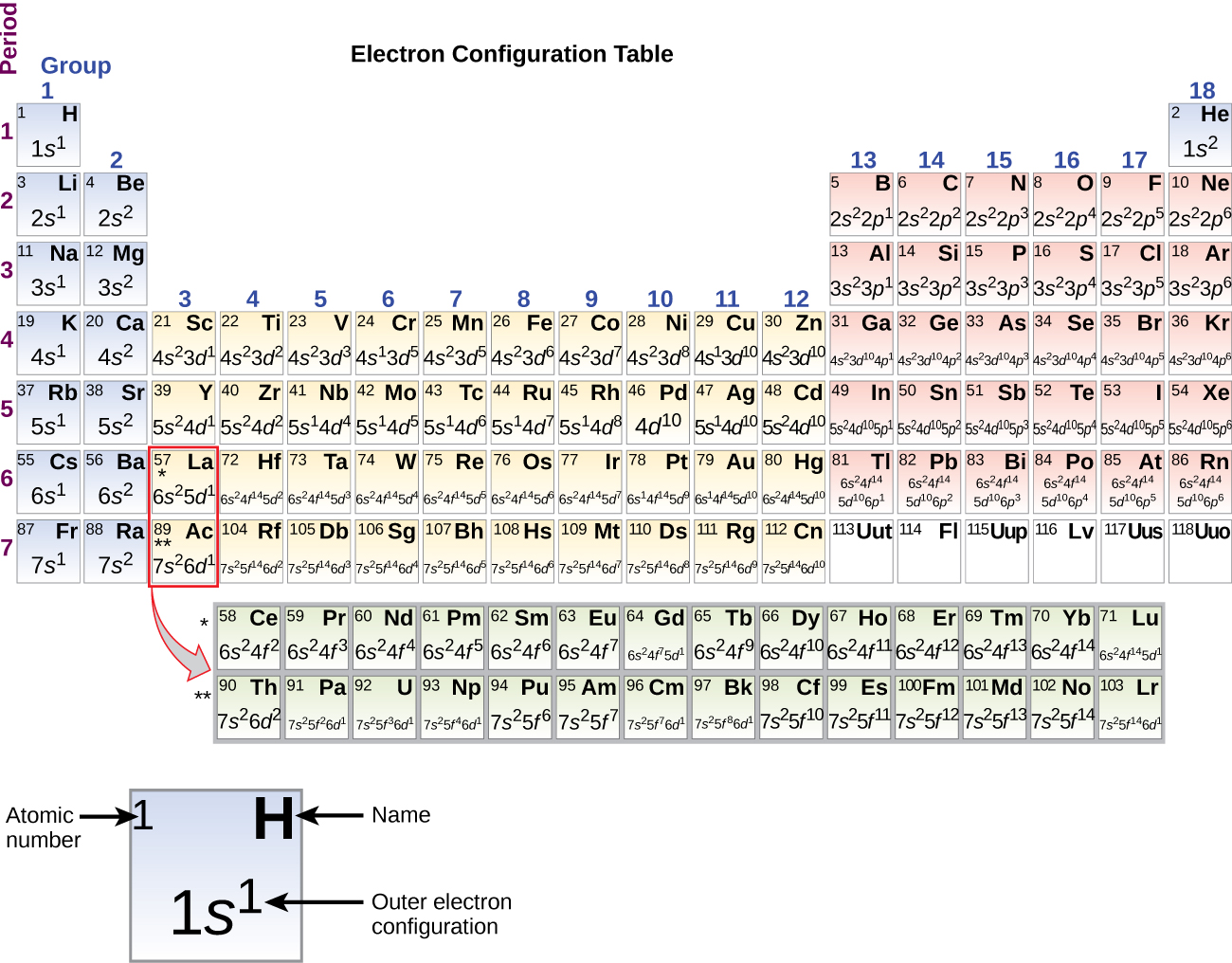Figure 2. This version of the periodic table shows the outer-shell electron configuration of each element. Note that down each group, the configuration is often similar.

Effective Nuclear Charge (Z_eff)

For an atom or an ion with only a single electron, we can calculate the potential energy of an electron by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. For example, in helium there are two electrons. From Coloumb’s law we know that there is a repulsive interaction that depends on the distance between them. In addition there are attractive interactions between each of the two electrons with the nucleus.  There are no known solutions to the Schrodinger equation for this problem, so one must use approximate methods to find the orbitals and their energies.

If an electron is far from the nucleus (i.e., if the distance r between the nucleus and the electron is large), then at any given moment, most of the other electrons will be between that electron and the nucleus. Hence these electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between the nucleus and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (Z_eff). An effective nuclear charge is the nuclear charge an electron actually experiences because of shielding from other electrons closer to the nucleus (Figure 3). Consequently, the Z_eff is always less than the actual nuclear charge, Z. The Z_eff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present.

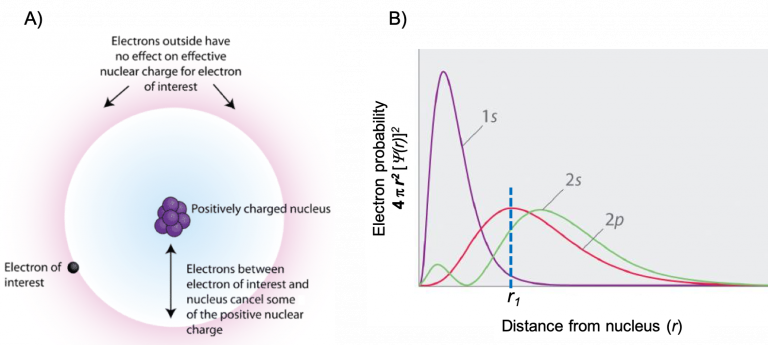
Shielding is determined by the probability of another electron being between the electron of interest and the nucleus, as well as by the electron–electron repulsions the electron of interest encounters. Core electrons are adept at shielding, while electrons in the same valence shell do not block the nuclear attraction experienced by each other as efficiently. In Figure 3B, if a 2p electron exists at a distance r₁, most likely the 1s electrons (core electrons) will be between the electron of interest and the nucleus. But, there is only a small probability of the 2s electron (electron in the same valence shell) to shield the 2p electron of interest. Thus, each time we move from one element to the next across a period, Z increases by one, but the shielding increases only slightly. Thus, Z_eff for valence electrons increases as we move from left to right across a period. In this class, we will calculate Z_eff = Z – S, where S is the number of core electrons that are shielding the valence electrons. There are more exact ways of determining Z_eff which include the shielding contribution of electrons in the same shell, but the approximate formula we use in this course is accurate enough to be very useful. Remember from earlier, Z is the number of protons in the nucleus. Note that while we often refer to the Z_eff of a valence electron, we can calculate the Z_eff for any electron by taking into account only the number of core electrons that are shielding. For example, consider a 2s electron of Cl. For Cl, Z = 17 and the electron configuration is 1s²2s²2p⁶3s²3p⁵. The only electrons that will shield a 2s electron are the 1s electrons, and there are two of them. Therefore, Z_eff = 17 – 2 = 15 for a 2s electron of Cl. The Z_eff for a 3p electron, on the other hand, is Z_eff = 17 – 10 = 7 because there are 10 electrons shielding the 3p electron (2 electrons in n = 1 and a total of 8 electrons in n = 2).

Electron Configurations and Chemical Reactivity

As described earlier, the Periodic Table arranges atoms based on increasing atomic number so that elements with the same chemical properties recur periodically. Because they are in the outer shells of an atom, valence electrons play the most important role in chemical reactions. The valence electrons (outer electrons) have the highest energy of the electrons in an atom and are more easily lost or shared than the core electrons. Valence electrons are also the determining factor in some physical properties of the elements.

Elements in any one group (or column) have the same number of valence electrons; the alkali metals (e.g. lithium and sodium) each have only one valence electron, the alkaline earth metals (e.g. beryllium and magnesium) each have two, and the halogens (e.g. fluorine and chlorine) each have seven valence electrons. The similarity in chemical properties among elements of the same group occurs because they have the same number of valence electrons. It is the loss, gain, or sharing of valence electrons that defines how elements react.

It is important to remember that the Periodic Table was developed on the basis of the chemical behavior of the elements, well before any idea of their atomic structure was available. Now we can understand why the Periodic Table has the arrangement it has—the arrangement puts elements whose atoms have the same number of valence electrons in the same group. This arrangement is emphasized in Figure 2 above, which shows, in Periodic-Table form, the electron configuration of the last subshell to be filled by the Aufbau principle. The colored sections of Figure 2 show the three categories of elements classified by the orbitals being filled: main group, transition, and inner transition elements. These classifications determine which orbitals are counted in the valence shell, or highest energy level orbitals of an atom.

1. Main group elements (sometimes called representative elements) are those in which the last electron added enters an s or a p orbital in the outermost shell, shown in blue and red in Figure 2. This category includes all the nonmetallic elements, as well as many metals and the intermediate semimetallic elements. The valence electrons for main group elements are those with the highest n level. For example, gallium (Ga, atomic number 31) has the electron configuration [Ar]4s²3d¹⁰4p¹, which contains three valence electrons (underlined). The completely filled d orbitals count as core, not valence, electrons.
2. Transition elements or transition metals. These are metallic elements in which the last electron added enters a d orbital. The valence electrons (those added after the last noble gas configuration) in these elements include the ns and (n – 1) d electrons. The official IUPAC definition of transition elements specifies those with partially filled d orbitals. Thus, the elements with completely filled orbitals (Zn, Cd, Hg, as well as Cu, Ag, and Au in Figure 2) are not technically transition elements. However, the term is frequently used to refer to the entire d block (colored yellow in Figure 2), and we will adopt this usage in this textbook.
3. Inner transition elements are metallic elements in which the last electron added occupies an f orbital. They are shown in green in Figure 2. The valence shells of the inner transition elements consist of the (n – 2)f, the (n – 1)d, and the ns subshells. There are two inner transition series:
   1. The lanthanide series: lanthanum (La) through lutetium (Lu)
   2. The actinide series: actinium (Ac) through lawrencium (Lr)

Lanthanum and actinium, because of their similarities to the other members of the series, are included and used to name the series, even though they are transition metals with no f electrons.