Solutions
Introduction to Solution Chemistry
Solutions are defined as homogeneous mixtures of two or more substances. Often, one component of a solution is present at a significantly greater concentration, in which case it is called the solvent. The other components of the solution present in relatively lesser concentrations are called solutes. Sugar is a covalent solid composed of sucrose molecules, C12H22O11. When this compound dissolves in water, its molecules become uniformly distributed among the molecules of water:
C12H22O11(s) ⟶ C12H22O11(aq)
The parenthetical “aq” in the equation signifies that the sucrose molecules are solutes and are therefore individually dispersed throughout the aqueous solution (water is the solvent). Although sucrose molecules are heavier than water molecules, they remain dispersed throughout the solution; gravity does not cause them to “settle out” over time.
Potassium dichromate, K2Cr2O7, is an ionic compound composed of colorless potassium ions, K+, and orange dichromate ions, Cr2O72-. When a small amount of solid potassium dichromate is added to water, the compound dissolves and dissociates to yield potassium ions and dichromate ions uniformly distributed throughout the mixture (Figure 1), as indicated in this equation:
K2Cr2O7(s) ⟶ 2 K+(aq) + Cr2O72-(aq)
As with the mixture of sugar and water, this potassium dichromate mixture is also an aqueous solution. Its solutes, potassium and dichromate ions, remain individually dispersed among the solvent (water) molecules.

Water is used so often as a solvent that the word solution has come to imply an aqueous solution to many people. However, almost any gas, liquid, or solid can act as a solvent.
Solutions exhibit these defining traits:
- They are homogeneous; that is, after a solution is mixed, it has the same composition at all points throughout (its composition is uniform).
- The components of a solution are dispersed on a molecular scale; that is, they consist of a mixture of separated molecules, atoms, and/or ions.
- The dissolved solute in a solution will not settle out or separate from the solvent.

Mixtures—samples of matter containing two or more substances physically combined—are more commonly encountered in nature than are pure substances. Similar to a pure substance, the relative composition of a mixture plays an important role in determining its properties. The relative amount of oxygen in a planet’s atmosphere determines its ability to sustain aerobic life. The relative amounts of iron, carbon, nickel, and other elements in steel (a mixture known as an “alloy”) determine its physical strength and resistance to corrosion. The relative amount of the active ingredient in a medicine determines its effectiveness in achieving the desired pharmacological effect. The relative amount of sugar in a beverage determines its sweetness (Figure 1). Here, we will describe one of the most common ways in which the relative compositions of mixtures may be quantified.
Solutions & Molarity
We have previously defined solutions as homogeneous mixtures, meaning that the composition of the mixture (and therefore its properties) is uniform throughout its entire volume. Solutions occur frequently in nature and have also been implemented in many forms of manmade technology.
The relative amount of a given solution component is known as its concentration. Often, though not always, a solution contains one component with a concentration that is significantly greater than that of all other components. This component is called the solvent and may be viewed as the medium in which the other components are dispersed, or dissolved. Solutions in which water is the solvent are, of course, very common on our planet. A solution in which water is the solvent is called an aqueous solution (indicated by (aq) in a chemical reaction).
A solute is a component of a solution that is typically present at a much lower concentration than the solvent. Solute concentrations are often described with qualitative terms such as dilute (of relatively low concentration) and concentrated (of relatively high concentration).
Concentrations may be quantitatively assessed using a wide variety of measurement units, each convenient for particular applications. Molarity (M), or molar concentration, is a useful concentration unit for many applications in chemistry. Molarity is defined as the number of moles of solute in exactly 1 liter (1 L) of the solution:
M = ![]()
Students often get confused with the use of the terms molarity and molar. The terms molarity and molar are synonymous, but have different uses. For example, if you have a solution that is labeled “3.5 M”. We could say that the molarity (or molar concentration) of the solution is 3.5, or we could say that the solution is 3.5 molar. We would not typically read “3.5 M” as “3.5 molarity”.
Also notice that due to the definition of molarity, if you are provided with a molarity, you are inherently provided with a conversion factor between moles of solute and liters of solution (this is similar to how we can think about density as a conversion factor, or ratio, of mass to volume of a substance).
Example 1: Calculating Molar Concentrations
A 355 mL soft drink sample contains 0.133 mol of sucrose (table sugar). What is the molar concentration of sucrose in the beverage?
Solution
Since the moles of solute and the volume of solution are both given, the molarity can be calculated using the definition of molarity. Per this definition, the solution volume must be converted from mL to L:
M = ![]() =
= ![]() = 0.375 M
= 0.375 M
Check Your Learning
A teaspoon of table sugar contains about 0.01 mol sucrose. What is the molarity of sucrose if a teaspoon of sugar has been dissolved in a cup of tea with a volume of 200 mL?
Answer
0.05 M
Example 2: Deriving Moles and Volumes from Molar Concentrations
How much sugar (mol) is contained in a modest sip (~10 mL) of the soft drink from Example 1?
Solution
In this case, we can rearrange the definition of molarity to isolate the quantity sought, moles of sugar. We then substitute the value for molarity that we derived in Example 1, 0.375 M:
M = ![]()
mol solute = M × L solution
mol solute = 0.375 ![]() ×
× ![]() = 0.004 mol sugar
= 0.004 mol sugar
Here we are using molarity as a conversion factor—since we know molarity and volume, we can find moles of substance.
Check Your Learning
What volume (mL) of the sweetened tea described in Example 1 contains the same amount of sugar (mol) as 10 mL of the soft drink in this example?
Answer
80 mL
Example 3: Calculating Molar Concentrations from the Mass of Solute
 Distilled white vinegar is a solution of acetic acid, CH3CO2H, in water. A 0.500 L vinegar solution contains 25.2 g of acetic acid. What is the concentration of the acetic acid solution in units of molarity?
Distilled white vinegar is a solution of acetic acid, CH3CO2H, in water. A 0.500 L vinegar solution contains 25.2 g of acetic acid. What is the concentration of the acetic acid solution in units of molarity?
Solution
As in the previous examples, the definition of molarity is the primary equation used to calculate the quantity sought. In this case, the mass of solute is provided instead of the amount of moles, so we must use the solute’s molar mass to obtain the amount of solute in moles:
M = ![]() = 0.839
= 0.839 ![]() = 0.839 M
= 0.839 M
Check Your Learning
Calculate the molarity of 6.52 g of CoCl2 (128.9 g/mol) dissolved in an aqueous solution with a total volume of 75.0 mL.
Answer
0.674 M
Example 4: Determining the Mass of Solute in a Given Volume of Solution
How many grams of NaCl are contained in 0.250 L of a 5.30 M solution?
Solution
The volume and molarity of the solution are specified, so the amount (mol) of solute is easily computed as demonstrated in Example 2:
M = ![]()
mol solute = M × L solution
mol solute = 5.30 ![]() × 0.250 L = 1.325 mol NaCl
× 0.250 L = 1.325 mol NaCl
Finally, this molar amount is used to derive the mass of NaCl:
1.325 mol NaCl × ![]() = 77.4 g NaCl
= 77.4 g NaCl
Another way of solving this problem, thinking of the concentration as a conversion factor between moles of solute and liters of solution is:
0.250 L solution × ![]() ×
× ![]() = 77.4 g NaCl
= 77.4 g NaCl
Check Your Learning
How many grams of CaCl2 (110.98 g/mol) are contained in 250.0 mL of a 0.200 M solution of calcium chloride?
Answer
5.55 g CaCl2
When performing calculations stepwise, as in Example 4, it is important to refrain from rounding any intermediate calculation results, which can lead to rounding errors in the final result. In Example 4, the molar amount of NaCl computed in the first step, 1.325 mol, would be properly rounded to 1.32 mol if it were to be reported; however, although the last digit (5) is not significant, it must be retained as a guard digit in the intermediate calculation. If we had not retained this guard digit, the final calculation for the mass of NaCl would have been 77.1 g, a difference of 0.3 g.
In addition to retaining a guard digit for intermediate calculations, we can also avoid rounding errors by performing computations in a single step (see Example 5). This eliminates intermediate steps so that only the final result is rounded.
Example 5: Determining the Volume of Solution Containing a Given Mass of Solute
In Example 3, we found the typical concentration of vinegar to be 0.839 M. What volume of vinegar contains 75.6 g of acetic acid?
Solution
First, use the molar mass to calculate moles of acetic acid from the given mass:
g solute × ![]() = mol solute
= mol solute
Then, use the molarity of the solution to calculate the volume of solution containing this molar amount of solute:
mol solute × ![]() = L solution
= L solution
Combining these two steps into one yields:
g solute × ![]() ×
× ![]() = L solution
= L solution
75.6 g CH3CO2H × ![]() ×
× ![]() = 1.50 L solution
= 1.50 L solution
Check Your Learning
What volume of a 1.50 M KBr solution contains 66.0 g KBr?
Answer
0.370 L
Dilution of Solutions

Dilution is the process whereby the concentration of a solution is lessened by the addition of solvent. For example, we might say that a glass of iced tea becomes diluted as the ice melts. The water from the melting ice increases the volume of the solvent (water) and the overall volume of the solution (iced tea), thereby reducing the relative concentrations of the solutes that give the beverage its taste (Figure 3).
Dilution is also a common means of preparing solutions of a desired concentration. By adding solvent to a measured portion of a more concentrated stock solution, we can achieve a particular concentration. For example, commercial pesticides are typically sold as solutions in which the active ingredients are far more concentrated than is appropriate for their application. Before they can be used on crops, the pesticides must be diluted. This is also a very common practice for the preparation of a number of common laboratory reagents (Figure 4).

A simple mathematical relationship can be used to relate the volumes and concentrations of a solution before and after the dilution process. According to the definition of molarity, the amount of moles of solute (n) in a solution is equal to the product of the solution’s molarity (M) and its volume in liters (L):
n = M × L
Expressions like these may be written for a solution before and after it is diluted:
n1 = M1 × L1
n2 = M2 × L2
where the subscripts “1” and “2” refer to the solution before and after the dilution, respectively. Since the dilution process does not change the amount of solute in the solution, n1 = n2. Thus, these two equations may be set equal to one another:
M1 × L1 = M2 × L2
This relation is commonly referred to as the dilution equation. Although we derived this equation using molarity as the unit of concentration and liters as the unit of volume, other units of concentration and volume may be used, so long as the units properly cancel per dimensional analysis. Reflecting this versatility, the dilution equation is often written in the more general form:
C1 × V1 = C2 × V2
where C and V are concentration and volume, respectively.
Example 6: Determining the Concentration of a Diluted Solution
If 0.850 L of a 5.00 M solution of copper nitrate, Cu(NO3)2, is diluted to a volume of 1.80 L by the addition of water, what is the molarity of the diluted solution?
Solution
We are given the volume and concentration of a stock solution, V1 and C1, and the volume of the resultant diluted solution, V2. We need to find the concentration of the diluted solution, C2. We thus rearrange the dilution equation in order to isolate C2:
C1 × V1 = C2 × V2
C2 = ![]()
Since the stock solution is being diluted by more than two-fold (volume is increased from 0.85 L to 1.80 L), we would expect the diluted solution’s concentration to be less than one-half 5 M. We will compare this ballpark estimate to the calculated result to check for any gross errors in computation (for example, such as an improper substitution of the given quantities). Substituting the given values for the terms on the right side of this equation yields:
C2 = ![]() = 2.36 M
= 2.36 M
This result compares well to our ballpark estimate (it’s a bit less than one-half the stock concentration, 5 M).
Check Your Learning
What is the concentration of the solution that results from diluting 25.0 mL of a 2.04 M solution of CH3OH to 500.0 mL?
Answer
0.102 M CH3OH
Example 7: Volume of a Diluted Solution
What volume of 0.12 M HBr can be prepared from 11 mL (0.011 L) of 0.45 M HBr?
Solution
We are given the volume and concentration of a stock solution, V1 and C1, and the concentration of the resultant diluted solution, C2. We need to find the volume of the diluted solution, V2. We thus rearrange the dilution equation in order to isolate V2:
C1 × V1 = C2 × V2
V2 = ![]()
Since the diluted concentration (0.12 M) is slightly more than one-fourth the original concentration (0.45 M), we would expect the volume of the diluted solution to be roughly four times the original volume, or around 44 mL. Substituting the given values and solving for the unknown volume yields:
V2 = ![]() = 0.041 L
= 0.041 L
The volume of the 0.12 M solution is 0.041 L (41 mL). The result is reasonable and compares well with our rough estimate.
Check Your Learning
A laboratory experiment calls for 0.125 M HNO3. What volume of 0.125 M HNO3 can be prepared from 0.250 L of 1.88 M HNO3?
Answer
3.76 L
Example 8: Volume of a Concentrated Solution Needed for Dilution
What volume of 1.59 M KOH is required to prepare 5.00 L of 0.100 M KOH?
Solution
We are given the concentration of a stock solution, C1, and the volume and concentration of the resultant diluted solution, V2 and C2. We need to find the volume of the stock solution, V1. We thus rearrange the dilution equation in order to isolate V1:
C1 × V1 = C2 × V2
V1 = ![]()
Since the concentration of the diluted solution 0.100 M is roughly one-sixteenth that of the stock solution (1.59 M), we would expect the volume of the stock solution to be about one-sixteenth that of the diluted solution, or around 0.3 liters. Substituting the given values and solving for the unknown volume yields:
V1 = ![]() = 0.314 L
= 0.314 L
Thus, we would need 0.314 L of the 1.59 M solution to prepare the desired solution. This result is consistent with our rough estimate.
Check Your Learning
What volume of a 0.575 M solution of glucose, C6H12O6, can be prepared from 50.00 mL of a 3.00 M glucose solution?
Answer
0.261 L
Solution Stoichiometry
Earlier, we learned that the coefficients of a balanced chemical equation provide the relative numbers of the chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. The process of using the coefficients in a balanced chemical equation to relate the amount of reactants and products can be summarized as in Figure 5.
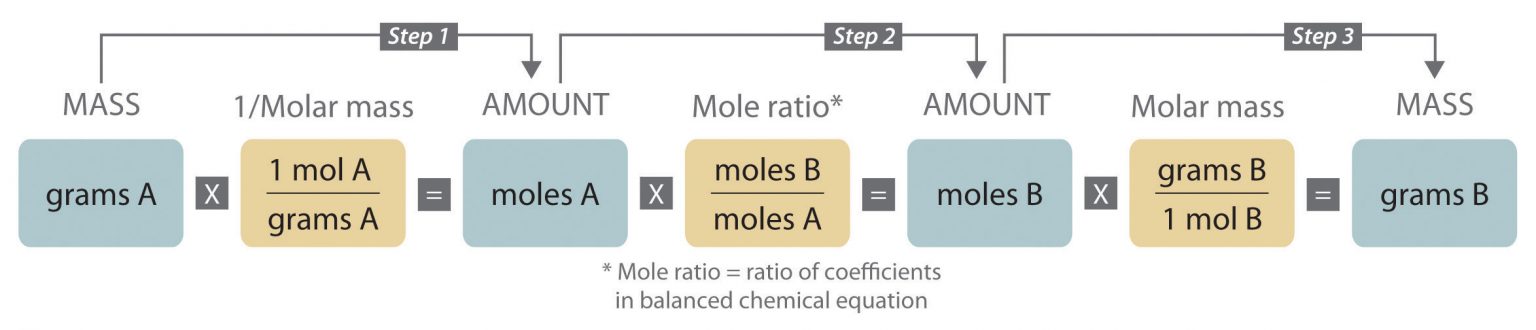
Since solutions offer a convenient medium for carrying out chemical reactions, it is often necessary to know how much of one solution will react with a given quantity of another. We can perform calculations similar to those outlined in Figure 5 by first using the volume of the solution and the concentration of the solution to determine how many moles of solute are present. This process is outlined in Figure 6.

The initial goal is the same for both procedures—convert to moles. You can accomplish this by either using mass and molar mass of a substance or by using volume and concentration of a solution. Once you have determined how many moles of a reactant or product are present, you can use the stoichiometric mole ratio to determine the quantity of the other reactants or products in the reaction.
Example 9: Solution Stoichiometry
Gold is extracted from its ores by treatment with an aqueous cyanide solution, which causes a reaction that forms the soluble [Au(CN)2]− ion. Gold is then recovered by reduction with metallic zinc according to the following equation:
Zn(s) + 2 [Au(CN)2]–(aq) → [Zn(CN)4]2-(aq) + 2 Au(s)
What mass of gold would you expect to recover from 400.0 L of a 3.30 × 10−4 M solution of [Au(CN)2]−?
Solution
First, we check the chemical equation to make sure it is balanced as written. Then we calculate the number of moles of [Au(CN)2]− present by multiplying the volume of the solution by its concentration. From the balanced chemical equation, we then use a mole ratio to calculate the number of moles of gold that can be obtained from the reaction. To calculate the mass of gold recovered, we multiply the number of moles of gold by its molar mass.
We can adapt Figure 6 to show this process as follows:
![A flow chart for stoichiometric calculations is shown. There are 7 boxes arranged horizontally. The first is shaded blue and labeled, “400.0 liters”. A multiplication sign is between the first and second box. The second box is shaded yellow and labeled “3.30e-4 moles [Au(CN) subscript 2]- divided by 1 liter”. The second box is followed by an equal sign. The third box is shaded blue and labeled “0.132 mol [Au(CN) subscript 2]-”. The third box is followed by a multiplication sign. The fourth box is shaded yellow and labeled “2 moles Au divided by 2 moles [Au(CN) subscript 2]-“. The fourth box is followed by an equal sign. The fifth box is shaded blue and labeled “0.132 mole Au”. The fifth box is followed by a multiplication sign. The sixth box is shaded yellow and labeled “196.67 g Au divided by 1 mol Au”. The sixth box is followed by an equal sign. The seventh and final box is shaded blue and labeled “26.0 g Au”.](https://wisc.pb.unizin.org/app/uploads/sites/763/2025/01/103_M4Q6_Ex9.jpg)
Check Your Learning
What mass of solid lanthanum(III) oxalate nonahydrate [La2(C2O4)3·9H2O] (molar mass = 703.87 g/mol) can be obtained from 650 mL of a 0.0170 M aqueous solution of LaCl3 by adding a stoichiometric amount of sodium oxalate (Na2C2O4)? The unbalanced reaction is as follows:
LaCl3(aq) + Na2C2O4(s) + H2O(ℓ) → La2(C2O4)3·9H2O(s) + NaCl(aq)
Answer
3.89 g
Example 10: Limiting Reactants in Solution
When aqueous solutions of silver nitrate and potassium dichromate are mixed, an exchange reaction occurs, and silver dichromate is obtained as a red solid. The overall chemical equation for the reaction is as follows:
2 AgNO3(aq) + K2Cr2O7(aq) → Ag2Cr2O7(s) + 2 KNO3(aq)
What mass of Ag2Cr2O7 is formed when 500 mL of 0.17 M K2Cr2O7 are mixed with 250 mL of 0.57 M AgNO3?
Solution
First, calculate the number of moles of each reactant by multiplying the volume of each solution by its molarity.
mol K2Cr2O7 = 500 mL × ![]() ×
× ![]() = 0.085 mol K2Cr2O7
= 0.085 mol K2Cr2O7
mol AgNO3 = 250 mL × ![]() ×
× ![]() = 0.14 mol AgNO3
= 0.14 mol AgNO3
Then, determine the limiting reactant by calculating the moles of Ag2Cr2O7 produced if each reactant were completely reacted.
0.085 mol K2Cr2O7 × ![]() = 0.085 mol Ag2Cr2O7
= 0.085 mol Ag2Cr2O7
0.14 mol AgNO3 ![]() = 0.071 mol Ag2Cr2O7
= 0.071 mol Ag2Cr2O7
Since complete reaction of AgNO3 produces less product (Ag2Cr2O7), AgNO3 is the limiting reactant and K2Cr2O7 is the excess reactant.
To find what mass of Ag2Cr2O7 is formed, we use the molar mass (431.72 g/mol):
0.071 mol Ag2Cr2O7 × ![]() = 30.8 g Ag2Cr2O7
= 30.8 g Ag2Cr2O7
Check Your Learning
Aqueous solutions of sodium bicarbonate and sulfuric acid react to produce carbon dioxide according to the following equation:
2 NaHCO3(aq) + H2SO4(aq) → 2 CO2(g) + Na2SO4(aq) + 2 H2O(ℓ)
If 13.0 mL of 3.0 M H2SO4 are added to 732 mL of 0.112 M NaHCO3, what mass of CO2 is produced?
Answer
3.4 g

