Up to now the major types of change we have considered are phase changes (solid to liquid, liquid to gas, etc.) Now we will look at the elements of a phase change in greater detail starting with temperature. If you look up the definition of temperature you will probably find something like “the degree of heat of an object” and think to yourself, “Well, that’s not very illuminating, is it?” However, it is actually quite difficult to give a simple definition of temperature, (typically abbreviated as T).

A useful macroscopic way of thinking about temperature is that it tells you in which direction thermal energy (often called heat) will move—energy always moves from a hotter (higher-temperature) object to a cooler (lower-temperature) one. This may seem like an obvious statement about how the physical world works but do you really know why it must be the case? Why doesn’t heat flow from cooler to warmer? Is there some principle that will allow us to to explain why? We will be coming back to these questions later on in this chapter.

Students often confuse temperature and thermal energy and before we go on we need to have a good grasp of the difference between them. The temperature of an object is independent of the size of the object, at least until we get down to the atomic/molecular level where temperature begins to lose its meaning as a concept.^[1] The temperature of a drop of boiling water is the same as the temperature of a pan (or an ocean) of boiling water: 100 °C at sea level. At the same time the total amount of thermal energy in a drop of water is much less than that in a large pot of water at the same temperature. A drop of boiling water may sting for a moment if it lands on you, but a pan of boiling water will cause serious damage if it splashes over you. Why? Even though the two are at the same temperature, one has relatively little thermal energy and the other has a lot; the amount of energy is related to the size of the system. In addition, the amount of thermal energy depends on the type, that is, the composition of the material. Different amounts of different substances can have different amounts of thermal energy, even if they are at the same temperature (weird but true).

Kinetic Energy and Temperature

Another way of thinking about temperature is that it is related to the energy of the particles in the sample: the faster the particles are moving, the higher the temperature. It may well take different amounts of energy to get particles moving at the same average kinetic energy. For a simple monoatomic gas, like helium or neon, the only motion that the atoms can do is to move from one place to another in a straight line until they bump into something else, such as another atom or molecule.^[2] This kind of motion is called translational motion and is directly linked to the kinetic energy of the atom or molecule through the relationship

where is the average of the square of velocity of all of the molecules in the population, m is the mass, R is a constant, and T is the temperature. That is, the average kinetic energy of a gas is directly related to the temperature. In any given gaseous sample of moving atoms there are many collisions per unit time but these collisions do not alter the total energy of the system (it is conserved).^[3] What these collision can, and often do, alter is the relative kinetic energies of the two (or more) colliding atoms: if one slows down, the other will speed up (remember, we are now talking only about monoatomic species; things get more complicated with more complex molecules).

Any single atom or molecule has kinetic energy, but not a temperature. This is an important distinction. Populations of molecules have a temperature related to their average velocity but the concept of temperature is not relevant to individual molecules, they have kinetic energy but not a temperature. This is a important idea, temperature as a characteristic of a system not its individual components. While a system has a unique temperature, the individual molecules that make up the system can have quite different kinetic energies. Because of collisions between molecules, an individual molecule’s kinetic energy can be changing rapidly, even though the temperature of the system is constant. When it comes to chemical reactions, it is individual kinetic energies that will be critical.

Thinking About Populations of Molecules

Within a population of atoms and molecules, the many collisions that occur per second lead to a range of speeds and directions (that is, velocities) of the atoms/molecules. When large numbers of particles are involved in a phenomenon, their individual actions are not important, for example when measuring temperature or pressure (although they are when individual molecules collide, that is, take part in chemical reactions). We treat large numbers of molecules as a population. A population is characterized by the distribution of the number or probability of molecules moving with various velocities.^[4] This makes it possible to use statistical methods to characterize the behavior of the population. Although any particular molecule behaves differently from one moment to the next, depending upon whether it collides with other molecules or not, the behavior of the population is quite predictable.^[5]

From this population perspective, it is the distribution of kinetic energies of atoms or molecules that depends upon the temperature of the system. We will not concern ourselves with deriving the equations that describe these relationships, but rather focus on a general description of the behavior of the motions of atoms and molecules in various states of matter.

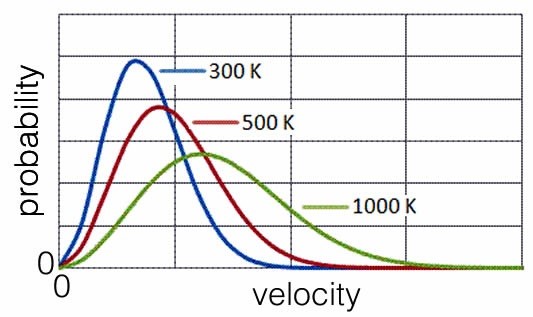
Let us think about a population of molecules at a particular temperature in the gas phase. Because of their constant collisions with one another, the population of molecules has a distribution of speeds. We can calculate the probability of a particular molecule moving at a particular speed. This relationship is known as the Maxwell–Boltzmann distribution, shown in the graph. Its shape is a function of the temperature of the system; typically it rises fairly steeply from zero (all of the curves begin at zero – why is that do you think?) to a maximum, which then decreases and tails off at higher velocities (which correspond to higher kinetic energies). Because we are plotting probability versus kinetic energy (or rms velocity or speed) we can set the area under the curve to be equal to one (or any other constant). As the temperature changes, the area under the curve stays constant. Why? Because we are completely certain that each particle has some defined amount of kinetic energy (or velocity or speed), even if it is zero and even if we could not possibly know it (remember the uncertainty principle). As the temperature is increased, the relative number of particles that are moving at higher speeds and with more kinetic energy increases. The shape of the curve flattens out and becomes broader. There are still molecules moving very slowly, but there are relatively fewer of them. The most probable speed (the peak of the curve) and the average speed (which is a little higher since the curve is not symmetrical) increase as the temperature increases.

Temperature, Kinetic Energy and Gases

Now here is an unexpected fact: the average kinetic energies of molecules of any gas at the same temperature are equal (since KE_avg = 3/2RT, the identity of the gas does not matter). Let us think about how that could be true and what it implies about gases. Under most circumstances the molecules in a gas do not significantly interact with each other; all they do is collide with one another like billiard balls. So when two gases are at the same temperature, their molecules have the same average kinetic energy. However, an even more unexpected fact is that the mass of the molecules of one gas is different from the mass of the molecules of the other gas. Therefore, given that the average kinetic energies are the same, but the molecular masses are different, the average velocities of molecules in the two gases must be different.

For example, let us compare molecular hydrogen (H₂ ) gas (molecular weight = 2 g/mol) with molecular oxygen (O₂) gas (molecular weight = 32 g/mol), at the same temperature. Since they are at the same temperature the average kinetic energy of H₂  must be equal to the average kinetic energy of O₂, then the H₂ molecules must be moving, on average, faster than the O₂ molecules.^[6]

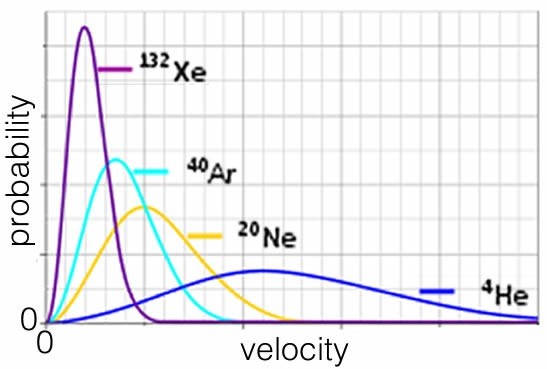
So the average speed at which an atom or molecule moves depends on its mass. Heavier particles move more slowly, on average, which makes perfect sense. Consider a plot of the behavior of the noble (monoatomic) gases, all at the same temperature. On average helium atoms move much faster than xenon atoms, which are over 30 times heavier. As a side note, gas molecules tend to move very fast. At 0 °C the average H₂ molecule is moving at about 2000 m/s, which is more than a mile per second and the average O₂ molecule is moving at approximately 500 m/s.