D11.4 Activation Energy, Concentration, and Reaction Rate

Jia Zhou; John Moore; Etienne Garand

D11.4 Activation Energy, Concentration, and Reaction Rate

The Arrhenius equation enables calculation of the rate constant at a given temperature. The rate law enables calculation of the rate, given k and concentrations of species that affect the rate. The previous section outlined one way to determine the rate law. In this section we illustrate how to experimentally determine the activation energy.

Exercise: Calculating Rate Constants

If we take the natural logarithm of both sides of the Arrhenius equation, we have:

$\text{ln}(k)\; =\; \text{ln}(A)\; +\; \left(-\dfrac{E_a}{RT}\right)$

which has a standard linear equation format:

$\begin{array}{rcccl} \text{ln}(k) & = & \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T}\right) &+& \text{ln}(A) \\[0.5em] y &=& m\ \ \ \ x &+& b \end{array}$

This provides a way to experimentally measure the activation energy of a reaction (the transition state structures are so short-lived that it is often impossible to characterize them experimentally). By measuring k at different temperatures and plotting ln(k) versus 1/T, we can obtain a straight line where slope = –E_a/R.

Activity: Determining E_a

You can estimate the activation energy without constructing an Arrhenius plot if the rate constant was measured at only two temperatures. The slope of an Arrhenius plot is:

$\text{Slope} = \dfrac{{\Delta}(\text{ln}\;k)}{{\Delta}\left(\dfrac{1}{T}\right)} = -\dfrac{E_{\text{a}}}{R}$

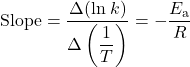
Therefore:

$\dfrac{\text{ln}(k_1)-\text{ln}(k_2)}{\dfrac{1}{T_1}-\dfrac{1}{T_2}} = -\dfrac{E_{\text{a}}}{R}$

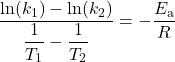
which can be rearranged as:

$\text{ln}\left(\dfrac{k_1}{k_2}\right) = -\dfrac{E_{\text{a}}}{R}\left(\dfrac{1}{T_1}\;-\;\dfrac{1}{T_2}\right)$

Left-click here for different forms of the equation

The negative sign on the right hand side of the equation can be included in the temperature term:

$\text{ln}\left(\dfrac{k_1}{k_2}\right) = \dfrac{E_{\text{a}}}{R}\left(\dfrac{-1}{T_1} - \dfrac{-1}{T_2}\right)$

$\text{ln}\left(\dfrac{k_1}{k_2}\right) = \dfrac{E_{\text{a}}}{R}\left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right)$

Alternatively, you can also multiply both side of the equation by -1 and obtain:

$-\text{ln}\left(\dfrac{k_1}{k_2}\right) = \dfrac{E_{\text{a}}}{R}\left(\dfrac{1}{T_1} - \dfrac{1}{T_2}\right)$

$\text{ln}\left(\dfrac{k_2}{k_1}\right) = \dfrac{E_{\text{a}}}{R}\left(\dfrac{1}{T_1} - \dfrac{1}{T_2}\right)$

Whichever form of the equation you use, keep careful track of the subscripts on the variables k₁, T₁, k₂, and T₂.

Left-click here for a different derivation of the equation

You can obtain the same equation by subtracting the Arrhenius equation with k₂ and T₂ from the Arrhenius equation with k₁ and T₁.

At T₁:

$\text{ln}(k_1) = \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_1}\right) + \text{ln}(A)$

At T₂:

$\text{ln}(k_2) = \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_2}\right) + \text{ln}(A)$

Subtracting the two:

$\text{ln}(k_1) - \text{ln}(k_2) = \left[\left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_1}\right) + \text{ln}(A)\right] - \left[\left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_2}\right) + \text{ln}(A)\right]$

$\text{ln}\left(\dfrac{k_1}{k_2}\right) = \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_1}\right) - \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_2}\right) + \text{ln}(A) - \text{ln}(A) = \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T_1}-\dfrac{1}{T_2}\right)$

Comments
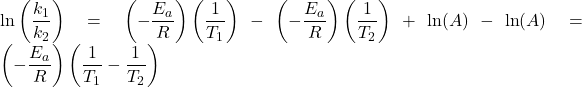
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 104 Summer 2024 Copyright © by Jia Zhou; John Moore; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.