D7.3 Equilibrium Constant Expressions

Jia Zhou; John Moore; Etienne Garand

D7.3 Equilibrium Constant Expressions

An equilibrium constant (K ) is a ratio of equilibrium partial pressures (gas-phase reaction) or equilibrium concentrations (solution-phase reaction) of products and reactants that has a specific value for a given reaction at a given temperature. For example, consider this generic reaction:

m A + n B ⇌ x C + y D

If the equation represents a gas-phase reaction, the equilibrium constant, K, is:

$K = \dfrac{p_{\text{C}}^{x}\ p_{\text{D}}^{y}}{p_{\text{A}}^{m}\ p_{\text{B}}^{n}}$

This mathematical expression is called the equilibrium constant expression for a gas-phase reaction. Each p in the expression represents the numeric value of the partial pressure of a gaseous product (numerator) or reactant (denominator) when the reaction is at equilibrium. Each partial pressure is raised to the power of its coefficient in the balanced equation. The partial pressures must be expressed in units of bar and only the number of bars is entered into the K expression. Because only numbers are entered into the expression, K has no units. (You will learn more about why K has no units later in this course.)

If the equation is for a reaction that occurs in solution, the K expression is:

$K = \dfrac{[\text{C}]^{x}[\text{D}]^{y}}{[\text{A}]^{m}[\text{B}]^{n}}$

Square brackets represent concentration in M (mol/L), so “[A]” represents the numeric value of the equilibrium concentration of reactant A. Each concentration value is raised to the power of its coefficient. Concentrations must be in expressed in mol/L and only numbers are entered into the K expression, so K has no units.

In general, K expressions include only substances whose partial pressures or concentrations change as a reaction proceeds. In other words, K expressions do not contain terms for pure solids or pure liquids. For example, consider the equilibrium constant expression for this reaction:

2 HgO(s) ⇌ 2 Hg(ℓ) + O₂(g) $K = p_{{\text{O}}_2}$

Because HgO is a solid, the number of HgO formula units per unit volume depends only on the density of HgO at the temperature of the reaction. In other words, the concentration of HgO(s) is the same throughout the reaction, and does not change as HgO is consumed or produced. Similarly, the number of Hg atoms per unit volume of Hg(ℓ) is constant throughout the reaction. Thus, these concentrations are not included in the K expression. It is necessary for some HgO(s) and some Hg(ℓ) to be present for the equilibrium to be maintained, but the total quantity of each does not affect the equilibrium.

In addition, for dilute solutions, the concentration of the solvent remains constant throughout the reaction and is also not included in the K expression, even though the solvent sometimes appears in the reaction equation.

A homogeneous equilibrium is one in which all of the reactants and products are present in a single phase. Examples of homogeneous equilibria are reactions in the gas phase and reactions in liquid solutions. For example:

C₂H₂(g) + 2 Br₂(g) ⇌ C₂H₂Br₄(g) $K = \dfrac{p_{\text{C}_2\text{H}_2\text{Br}_4}}{p_{\text{C}_2\text{H}_2}\ p_{\text{Br}_2}^{2}}$

I₂(aq) + I⁻(aq) ⇌ I₃⁻(aq) $K = \dfrac{[\text{I}_3^{-}]}{[\text{I}_2] [\text{I}^{-}]}$

Hg₂²⁺(aq) + NO₃⁻(aq) + 3 H₃O⁺(aq) ⇌ 2 Hg²⁺(aq) + HNO₂(aq) + 4H₂O(ℓ) $K = \dfrac{[\text{Hg}^{2+}]^{2}[\text{HNO}_2]}{[\text{Hg}_2^{2+}] [\text{NO}_3^{-}] [\text{H}_3\text{O}^{+}]^{3}}$

HF(aq) + H₂O(ℓ) ⇌ H₃O⁺(aq) + F⁻(aq) $K = \dfrac{[\text{H}_3\text{O}^{+}] [\text{F}^{-}]}{[\text{HF}]}$

NH₃(aq) + H₂O(ℓ) ⇌ NH₄⁺(aq) + OH⁻(aq) $K = \dfrac{[\text{NH}_4^{+}] [\text{OH}^{-}]}{[\text{NH}_3]}$

In the aqueous equilibrium systems, H₂O(ℓ) is the solvent. Its concentration does not appear in the K expression.

A heterogeneous equilibrium is a system in which reactants and products are found in two or more phases. Some heterogeneous equilibria involve chemical changes, for example:

PbCl₂(s) ⇌ Pb²⁺(aq) + 2 Cl⁻(aq) K = [Pb²⁺][Cl⁻]²

CaO(s) + CO₂(g) ⇌ CaCO₃(s) $K = \dfrac{1}{p_{\text{CO}_2}}$

C(s) + 2 S(g) ⇌ CS₂(g) $K = \dfrac{p_{\text{CS}_2}}{p_{\text{S}}^{2}}$

Other heterogeneous equilibria involve phase changes, for example:

Br₂(ℓ) ⇌ Br₂(g) $K = p_{{\text{Br}}_2}$

Working with K

There are a few things to keep in mind when working with equilibrium constant expressions.

When all the coefficients in a balanced chemical equation are multiplied by some factor n, then the new K is the original K raised to the n^th power. For example:

2 NO₂(g) ⇌ N₂O₄(g) $K_{1} = \dfrac{p_{\text{N}_2\text{O}_4}}{p_{\text{NO}_2}^{2}}$

NO₂(g) ⇌ ½ N₂O₄(g) $K_{2} = \dfrac{p_{\text{N}_2\text{O}_4}^{1/2}}{p_{\text{NO}_2}} = (K_{1})^{1/2}$

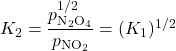
When a reaction’s direction is reversed, the K for the new reaction is the reciprocal (inverse) of the original reaction K. For example, consider these reactions in the gas phase:

A + 2B ⇌ AB₂ $K_{1} = \dfrac{p_{\text{AB}_2}}{p_{\text{A}}\ p_{\text{B}}^{2}}$

AB₂ ⇌ A + 2B $K_{2} = \dfrac{p_{\text{A}}\ p_{\text{B}}^{2}}{p_{\text{AB}_2}} = \dfrac{1}{K_{1}}$

When two reactions occur sequentially to yield a new overall reaction, the K for the overall reaction is the product of the K values for the individual steps. For example, consider these reactions in solution:

A + C ⇌ AC $K_{1} = \dfrac{[\text{AC}]}{[\text{A}] [\text{C}]}$

AC + C ⇌ AC₂ $K_{2} = \dfrac{[\text{AC}_2]}{[\text{AC}] [\text{C}]}$

A + 2 C ⇌ AC₂ $K_{3} = \dfrac{[\text{AC}_2]}{[\text{A}] [\text{C}]^{2}} = K_{1}\times K_{2}$

Exercise: Properties of Chemical Equilibrium

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 104 Summer 2024 Copyright © by Jia Zhou; John Moore; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.