D14.3 Equilibrium Approximation
When the rate-determining step is not the first step, the rate law of the overall reaction can still be approximated as the rate law for the rate-determining step. However, one or more of the reactants involved in such a rate-determining step would be a reaction intermediate formed from a previous step. Hence, the rate law for the rate-determining step would include the concentration of a species that is rarely measurable. (Even if the concentration of a reaction intermediate can be measured experimentally, the accuracy is usually low because the concentration is very small.)
Experimentally determined rate laws are always expressed in terms of concentrations of reactants and/or products, for which accurate measurements are much easier to obtain. In order to compare the theoretical rate law derived from the mechanism to the experimentally determined rate law, we must express the mechanism rate law only in terms of reactant and product concentrations, that is, we cannot simply use the rate law of the rate-determining step as is (unless the rate-determining step is the first step).
In other words, it is necessary to express an intermediate’s concentration in terms of reactant and/or product concentrations. To do this, some approximation is usually needed. In one situation, where a preceding step that forms the reaction intermediate is at equilibrium, we can make use of the equilibrium approximation.
For an example, consider the following multi-step reaction:
The currently accepted mechanism for this reaction is:
| Step 1: | NO(g) + Cl2(g) | NOCl2(g) | fast | |
| Step 2: | NOCl2(g) + NO(g) | 2NOCl(g) | slow | |
| Overall: | 2NO(g) + Cl2(g) | ⟶ | 2NOCl(g) |
In this mechanism, step 1 has a smaller activation energy and hence a larger rate constant than step 2. Therefore step 2 is the rate-determining step, and its rate law is:
However, this rate law involves the concentration of an intermediate, [NOCl2], so it cannot be directly compared to experimental data. We need to express [NOCl2] in terms of concentrations of reactants.
When NO and Cl2 react to form NOCl2 with rate constant k1, there are two reactions possible for the NOCl2:
- it can decompose back to form NO and Cl2 with rate constant k-1
NOCl2(g)
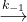 NO(g) + Cl2(g)
NO(g) + Cl2(g) - it can react with NO to form two NOCl with rate constant k2
NOCl2(g) + NO(g)
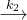 2 NOCl(g)
2 NOCl(g)
Because k2 << k-1, NOCl2 molecules are much more likely to decompose than to react in step 2. When enough NOCl2 has formed, we can approximate that the rate of its decomposition (rate-1) is equal to the rate at which it forms (rate1), meaning that step 1 is at equilibrium (rate1 = rate-1). This approximation gives us:
| rate1 | = | rate-1 |
| k1[NO][Cl2] | = | k-1[NOCl2] |
This relationship can be rearranged to solve for the concentration of NOCl2:
Substituting this expression into the rate law for step 2, we have:
If we make:
then the rate law for the overall reaction becomes:
This rate law can be compared with experimental data to determine whether the proposed mechanism is a plausible one.
Activity: Rate Law from Mechanism
A fellow student says that the reaction mechanism below is a plausible mechanism for this reaction:
2 NO(g) + O2(g) ⟶ 2 NO2(g) Rate = k[NO]2[O2]
Mechanism:
| Step 1 (fast): | NO(g) + O2(g) | NO3(g) | |
| Step 2 (slow): | NO3(g) + NO(g) | 2 NO2(g) |
Apply the criteria for an appropriate mechanism to explain why your fellow student is correct or incorrect. Write your rationale in your notebook.
Write in your notebook, then left-click here for an explanation.
Your fellow student is correct. This is a plausible mechanism.
- Each step in the mechanism is a bimolecular reaction, satisfying the criterion that a mechanism consists of unimolecular or bimolecular elementary reactions. The intermediate, NO3 is known to occur in some reactions; drawing a Lewis structure reveals that NO3 is a free radical (it has one electron less than nitrate ion, which has a complete octet on each atom). Since it is a free radical NO3 is not extremely stable, but it is stable enough to exist as an intermediate.
- The two reactions in the mechanism sum to the overall reaction given:
Step 1: NO(g) + O2(g) ⇌ NO3(g) Step 2: NO3(g) + NO(g) ⟶ 2 NO2(g) NO(g) + O2(g) + NO3(g)+ NO(g)⟶ NO3(g)+ 2 NO2(g)that is, 2 NO(g) + O2(g) ⟶ 2 NO2(g)
- The mechanism predicts the experimental rate law for the reaction:
The rate law for the slow step is the rate law for the reaction. Step 2 is the slow step, soRate = k2[NO3][NO]However, NO3 is an intermediate and its concentration is not easily measured. Therefore, we need to express the concentration of NO3 in terms of concentrations of reactants (or other species whose concentrations are easily measured).
Assuming that the first step is a rapid equilibrium, and the forward and reverse reaction of the first step occur at equal rates. Thenratestep 1, forward = ratestep 1, reverse
k1[NO][O2] = k−1[NO3]Solving for [NO3] gives
![Rendered by QuickLaTeX.com [\text{NO}_3] = \dfrac{k_1}{k_{-1}}[\text{NO}][\text{O}_2]](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-61323d0d9c0490ce500e610d921299cd_l3.png)
and so the predicted rate law is
![Rendered by QuickLaTeX.com Rate = k_2 [\text{NO}_3] [\text{NO}] = k_2 \left( \dfrac{k_1}{k_{-1}} [\text{NO}] [\text{O}_2]\right) [\text{NO}]](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-40cbe4a2be081ac8bbd12a0229aa7513_l3.png)
Because the product and quotient of constants is itself a constant, the rate law becomes
Rate = k[NO]2[O2]which agrees with the experimentally determined rate law.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

