D14.1 Multi-step Reactions and Rate-Determining Step

We now know how to experimentally measure the reaction orders and determine the value of k, which also informs us about activation energy and the frequency factor, but how do we use the experimentally determined rate law to assess whether a proposed reaction mechanism is likely to be correct?

A valid mechanism for a multi-step reaction has these characteristics:

• The mechanism should consist of a series of unimolecular and/or bimolecular elementary reaction steps that are plausible based on our knowledge of chemical bonding and interactions between molecules.
  • For example, if a step in a proposed mechanism involves three reactant species, it is very unlikely that this would be an elementary reaction, and therefore the mechanism is likely incorrect.
  • If a reaction step involves breaking a very strong bond, then it is unlikely to have a small enough activation energy to occur fast enough to make the mechanism work.
• The sum of the reaction steps should agree with the overall balanced reaction equation.
• The mechanism must agree with the experimentally observed rate law.

Let us consider the last point in more detail.

For some multi-step mechanisms, it is possible to derive the overall rate law from the known rate laws of the individual elementary steps (which can be derived directly from the stoichiometry of the chemical equations). If the experimentally determined rate law agrees with the theoretical rate law derived from the mechanism, the mechanism is a plausible theory for how the reaction occurs. If the mechanism predicts a rate law that is not the same as the experimentally observed rate law, then the mechanism must be incorrect. Other experimental data can further support the plausibility of a mechanism. For example, if an intermediate proposed in the mechanism is observed in the reaction mixture, that would support the mechanism.

Deriving the rate law from a reaction mechanism can be a complex task. However, for many multi-step reactions, one elementary reaction step is significantly slower than the other steps, and this step limits the rate at which the overall reaction occurs. This slowest step in a mechanism is called the rate-determining step (or rate-limiting step), and it allows for some simplifying approximations.

As an example of a rate-determining step, consider the oxidation of iodide ions by hydrogen peroxide in aqueous solution:

The currently accepted mechanism for this reaction has three steps. The third step occurs twice: each time the first step takes place and each time the second steps take place, so it is written twice.

Step 1:	H2O2(aq) + I–(aq)		HOI(aq) + OH–(aq)	Slow
Step 2:	HOI(aq) + I–(aq)		I2(aq) + OH–(aq)	Fast
Step 3:	OH–(aq) + H+(aq)		H2O(ℓ)	Fast
	OH–(aq) + H+(aq)		H2O(ℓ)

The first step is labeled “slow”, which conveys the idea that the rate constant k₁ is much smaller than the other two rate constants. Similarly, steps 2 and 3 are labeled “fast” to communicate that rate constants k₂ and k₃ are much larger than k₁.

However, keep in mind that the actual reaction rate of each step also depends on the concentrations of their reactants. Initially, steps 2 and 3 do not occur (rate = 0) because the concentration of one of their reactants is zero. For example, [HOI] = 0 M initially because HOI is not a reactant in the overall reaction. Thus, step 2 (rate_{step 2} = k₂[HOI][I^–]) cannot proceed forward until step 1 produces some HOI and raises [HOI] above zero. No matter how big k₂ might be, step 2 cannot go any faster than step 1. We say that the rate of step 2 is limited by the rate of step 1. Similarly, step 3 cannot occur until steps 1 and 2 produce some OH^–, so the rate of step 3 is also limited by the rate of step 1. Thus, in this case, step 1 is the rate-limiting step.

Activity: Reaction Energy Diagram

Consider the mechanism for oxidation of iodide ions by hydrogen peroxide shown below. The reaction is known to be exergonic.

Step 1:	H2O2(aq) + I–(aq)		HOI(aq) + OH–(aq)	Slow
Step 2:	HOI(aq) + I–(aq)		I2(aq) + OH–(aq)	Fast
Step 3:	OH–(aq) + H+(aq)		H2O(ℓ)	Fast
	OH–(aq) + H+(aq)		H2O(ℓ)

In your notebook, draw a reaction energy diagram corresponding to this mechanism. Label each minimum in the diagram with the atomic-level particles that are present at that stage in the reaction. Make certain that the relative energies of the transition states are shown accurately.

Note that there are two identical equations in step 3. This is because there is one OH⁻ ion produced in step 1 and one OH⁻ ion produced in step 2. Thus the reaction in step 3 happens twice. We could also write step 3 as

2 × [ OH⁻(aq) + H⁺(aq) H₂O(ℓ) ]

Draw in your notebook, then left-click here for an explanation.

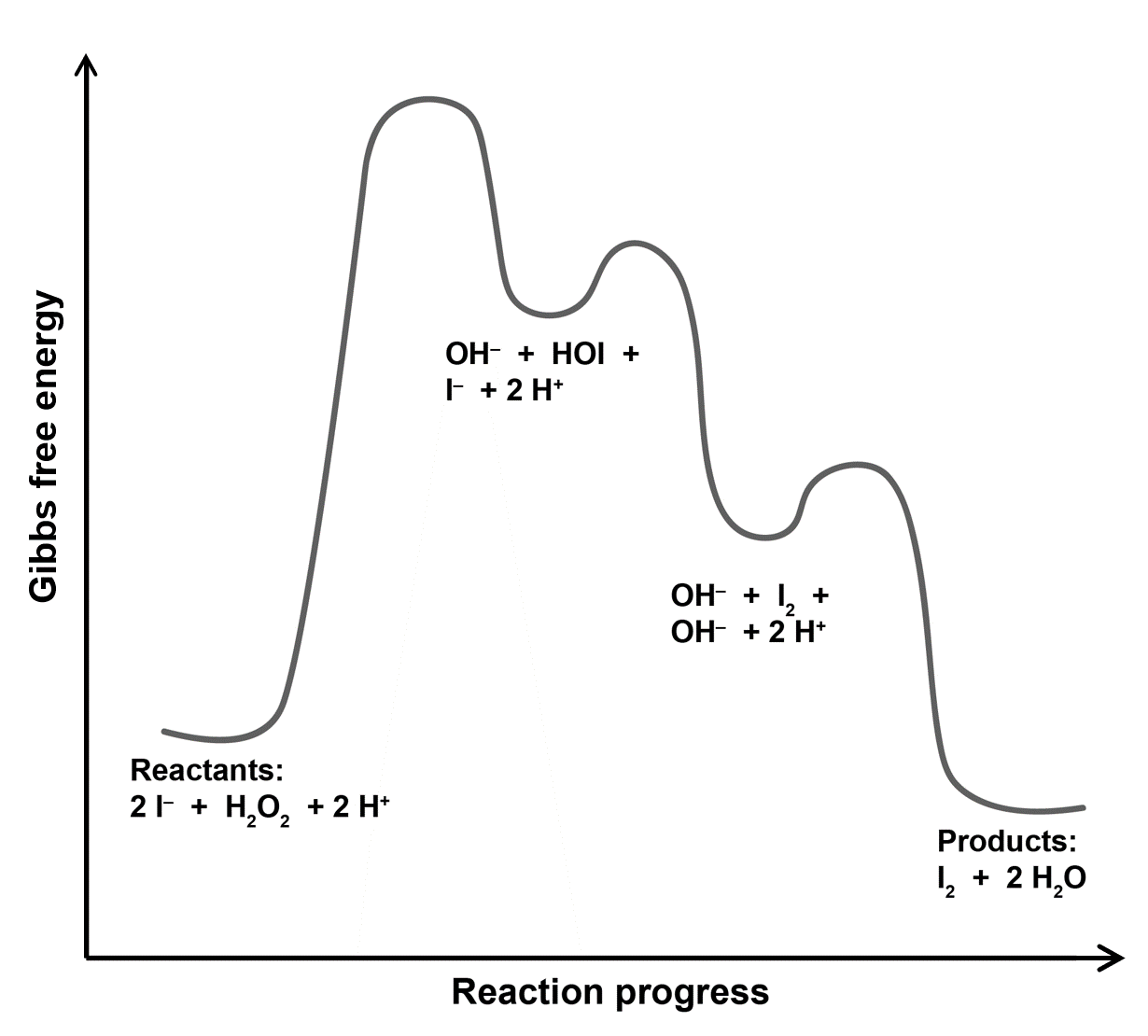The diagram has three maxima because the mechanism has three steps. Each maximum corresponds to the transition state of an elementary reaction step.

The initial energy is higher than the final energy because the reaction is exergonic. The initial energy corresponds to reactants. The reactants are 2I⁻, H₂O₂, and 2H⁺.

The first maximum is highest because the first step is slow (has smallest k and therefore highest activation energy).

The next minimum is products of step 1: HOI and OH⁻, and leftover reactants: I⁻ and 2H⁺.

The second maximum is lower than the first one and the activation energy of step 2 is smaller than that of step 1.

The second minimum is products of step 2: I₂ and OH⁻, unreacted products of step 1: OH^−, and leftover reactants: 2H⁺.

The last maximum is also lower than the first one and the activation energy of step 3 is also smaller than that of step 1. (There is no information on the difference between activation energy of step 3 and step 2.)

The final minimum is products: I₂ and 2H₂O.

Reaction intermediates are HOI, which is produced in step 1 and reacted away in step 2, and OH⁻, which is produced in steps 1 and 2 and reacted away in step 3.