D15.7 Radioactive Half-Lives

Determining the rate law and rate constant of a reaction has numerous real world applications, one of which involves the rate of radioactive decay, the spontaneous change of an unstable nuclide into a different nuclide. (A nuclide is an atomic species of a specific isotope.) The rate of radioactive decay allows scientists to learn about the histories of our world in geological and archaeological studies.

During a radioactive decay process, the unstable nuclide is called the parent nuclide, and the nuclide that results from the decay is called the daughter nuclide. The daughter nuclide may be stable, or it may decay itself. The atomic representations used when discussing radioactive decay reactions have two numbers written to the left of the atomic symbol, for example, and its isotope . The subscript denotes the atomic number, Z, of the element (number of protons), and the superscript denotes the mass number, A, of the isotope (number of protons + number of neutrons). Both subscript and superscript are necessary for balancing nuclear equations.

Most radioactive decay processes follow first-order kinetics, and have a characteristic constant half-life. A radioactive isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, or how long a sample of an undesirable or dangerous isotope must be stored before it decays to a sufficiently low radiation level.

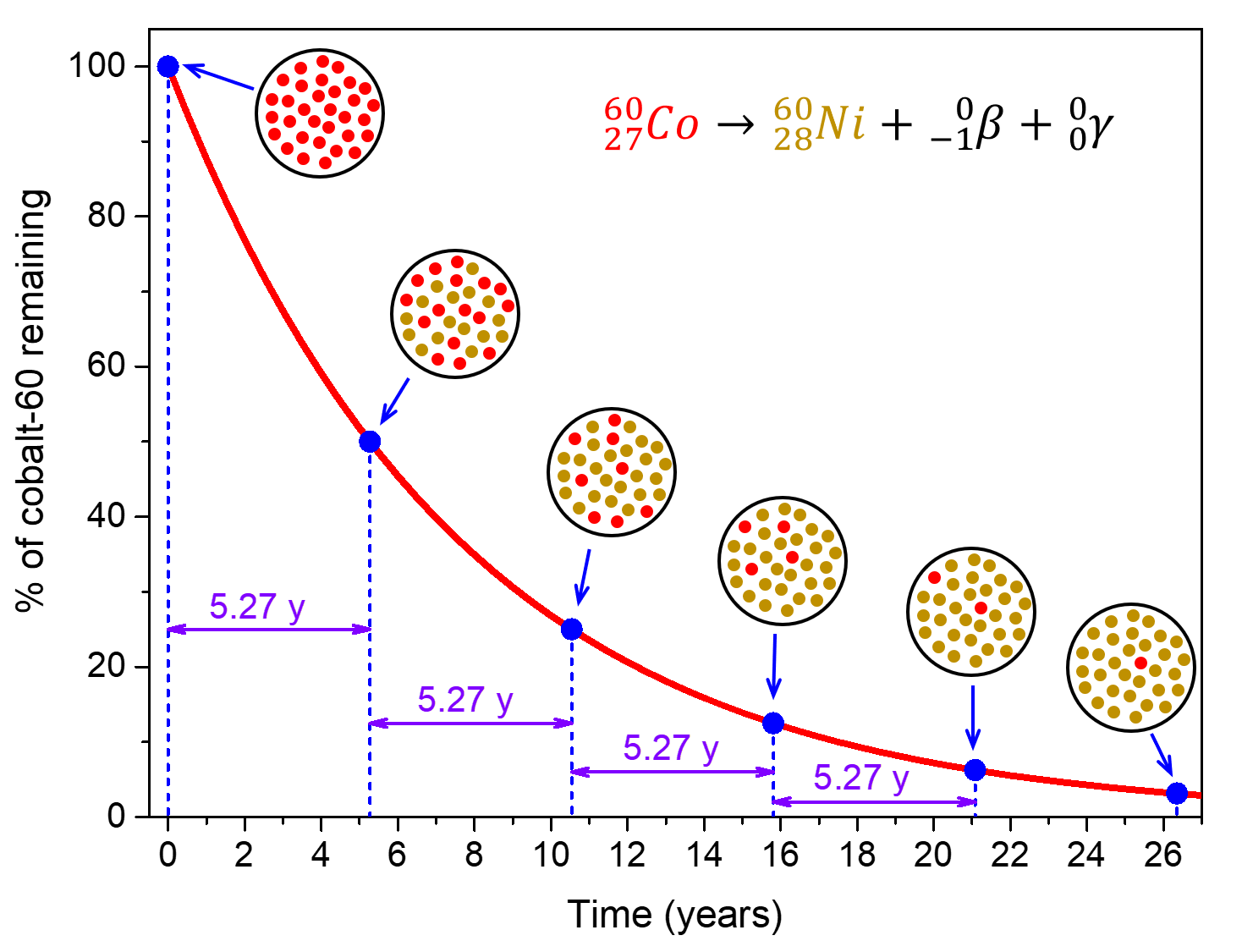
For example, cobalt-60 (), an isotope that emits gamma rays used to treat cancer, has t_½ = 5.27 years. Therefore, in a given cobalt-60 source, both the amount of and the intensity of the radiation emitted is cut in half every 5.27 years.

The number of nuclear transformations per unit time is called the activity, symbol A, of the radioactive sample. The activity of a sample can be measured with an instrument, such as a Geiger counter. The activity is directly proportional to the number of radioactive nuclei present, which is symbolized by N. The rate constant for nuclear decay is called the decay constant, symbol λ. Hence, the rate expression for radioactive decay is:

This is analogous to the first-order rate law for a chemical reaction, C ⟶ D + E,

Notice that in the case of radioactive decay, rate corresponds to A, [C] corresponds to N, and k corresponds to λ.

The other kinetic equations for first-order reactions similarly apply to radioactive decay, but with radioactive-decay-specific symbols:

Note that rather than concentration units (mol/L), N₀ and N_t have the units of moles or number of atoms. Because radioactivity is defined in terms of the number of radioactive nuclei, the activity increases as the mass of a radioactive sample increases.