D9.2 Second Law of Thermodynamics
The second law of thermodynamics enables predictions of whether a process, such as a chemical reaction, is spontaneous and whether the process is product-favored.
In thermodynamic models, the system and surroundings are defined to compose of everything (in other words, the system plus the surroundings is everything in the universe), therefore,
To illustrate this relationship, consider the process of heat transfer between two objects, one identified as the system and the other as the surroundings. There are three possibilities for such a process:
- The objects are at different temperatures, and energy transfers from the hotter object to the cooler object. This is always observed to occur. Designating the hotter object as the system and invoking the definition of entropy yields:
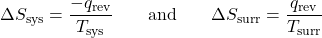
The arithmetic signs of qrev denote the loss of energy by the system and the gain of energy by the surroundings. Since Tsys > Tsurr in this scenario, ΔSsurr is positive and its magnitude is greater than the magnitude of ΔSsys. Thus, ΔSsys and ΔSsurr sum to a positive value for ΔSuniv. This process involves an increase in the entropy of the universe.
- The objects are at different temperatures, and energy transfers from the cooler object to the hotter object. This is never observed to occur. Again designating the hotter object as the system:
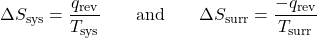
The magnitude of ΔSsurr is again greater than that for ΔSsys, but in this case, the sign of ΔSsurr is negative, yielding a negative value for ΔSuniv. This process involves a decrease in the entropy of the universe. (Note also that possibility 1, which is the reverse of this process, always occurs.)
- The temperature difference between the objects is infinitesimally small, Tsys ≈ Tsurr, and therefore the heat transfer is thermodynamically reversible. In this case, the system and surroundings experience entropy changes that are equal in magnitude and sum to a value of zero for ΔSuniv. This process involves no change in the entropy of the universe.
These results lead to the second law of thermodynamics: all changes that take place of their own accord (are spontaneous) involve an increase in the entropy of the universe.
| ΔSuniv > 0 | spontaneous (takes place of its own accord) |
| ΔSuniv < 0 | not spontaneous (reverse reaction would occur) |
| ΔSuniv = 0 | system is at equilibrium |
For many realistic applications, the surroundings are vast in comparison to the system. In such cases, the heat transfer to or from the surroundings would be a nearly infinitesimal fraction of its total thermal energy. For example, combustion of a hydrocarbon fuel in air involves heat transfer from a system (the fuel and oxygen molecules reacting to form carbon dioxide and water) to surroundings that are significantly more massive (Earth’s atmosphere). As a result, qsurr is a good approximation of qrev, and the second law of thermodynamics may be stated as:
We can use this equation to predict whether a process is spontaneous.
Activity: Enthalpy, Entropy, and Spontaneous Reactions
Under a particular set of conditions, the process:
H2O(s) ⟶ H2O(ℓ)
has entropy change of 22.1 J/K·mol and requires that the system be heated by 6.00 kJ/mol. Is the process spontaneous at −10.00 °C? Is it spontaneous at +10.00 °C? Explain your reasoning.
Write in your notebook, then left-click here for an explanation.
We can assess whether the process is spontaneous by calculating the entropy change of the universe. If ΔSuniv is positive, then the process is spontaneous. At both temperatures, ΔSsys = 22.1 J/K·mol and qsurr = −6.00 kJ/mol. (The system was heated by 6.00 kJ/mol, and qsurr = −qsys)
At −10.00 °C (263.15 K):
![Rendered by QuickLaTeX.com \begin{array}{rcl} {\Delta}S_{\text{univ}} &=& {\Delta}S_{\text{sys}} + {\Delta}S_{\text{surr}} = {\Delta}S_{\text{sys}} + \dfrac{q_{\text{surr}}}{T} \\[1em] &=& 22.1\;\frac{\text{J}}{\text{K·mol}} + \dfrac{-6.00 \times 10^3\;\text{J/mol}}{263.15\;\text{K}} = -0.7\;\frac {\text{J}}{\text{K·mol}} \end{array}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-29f44a751631ba2c633e4b083ead6a76_l3.png)
ΔSuniv < 0, so the process is not spontaneous at −10.0 °C. Ice does not melt under the specified conditions.
At 10.00 °C (283.15 K):
![Rendered by QuickLaTeX.com \begin{array}{rcl} {\Delta}S_{\text{univ}} &=& {\Delta}S_{\text{sys}} + \dfrac{q_{\text{surr}}}{T} \\[0.5em] &=& 22.1\;\frac{\text{J}}{\text{K·mol}} + \dfrac{-6.00 \times 10^3\;\text{J/mol}}{283.15\;\text{K}} = +0.9\;\frac{\text{J}}{\text{K·mol}} \end{array}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-5cc231d56f76c8416a55012ad2587e86_l3.png)
ΔSuniv > 0, so the process is spontaneous at 10.00 °C.
Suppose an exothermic chemical reaction takes place at constant atmospheric pressure. There is heat transfer of energy from the reaction system to the surroundings, qsurr = –qsys. The heat transfer for the system is the enthalpy change of the reaction because, at constant pressure, ΔrH° = q. Because the energy transfer to the surroundings is reversible, the entropy change for the surroundings can also be expressed as:
The same reasoning applies to an endothermic reaction: qsys and qsurr are equal but have opposite sign.
Also, for a chemical reaction system, ΔS°sys = ΔrS° (the standard entropy change for the reaction). Hence, ΔS°univ can be expressed as:
The convenience of this equation is that, for a given reaction, ΔS°univ can be calculated from thermodynamics data for the system only. That is, from data found in the Appendix. And the sign of ΔS°univ can tell you if a process will be spontaneous from a system starting point of standard state, which is also then related to whether the process is product-favored (ΔS°univ > 0) or reactant-favored (ΔS°univ < 0).
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

