D22.1 Standard Half-Cell Potentials
A cell potential results from the difference in the electrical potential between the half-cells. It is not possible to measure directly the potential of a single half-cell; one half-cell has to be connected to another half-cell to measure a voltage.
However, it is useful to tabulate potentials for individual half-cells, such that the potential for a voltaic cell constructed from any two half-cells can be calculated from the values in the table. To create such a table, all half-cell potentials need to be measured relative to the same reference half-cell. That half-cell is the standard hydrogen electrode (SHE), which consists of hydrogen gas at 1 bar pressure bubbling through a 1 M H+(aq) solution (platinum is used as the inert electrode):
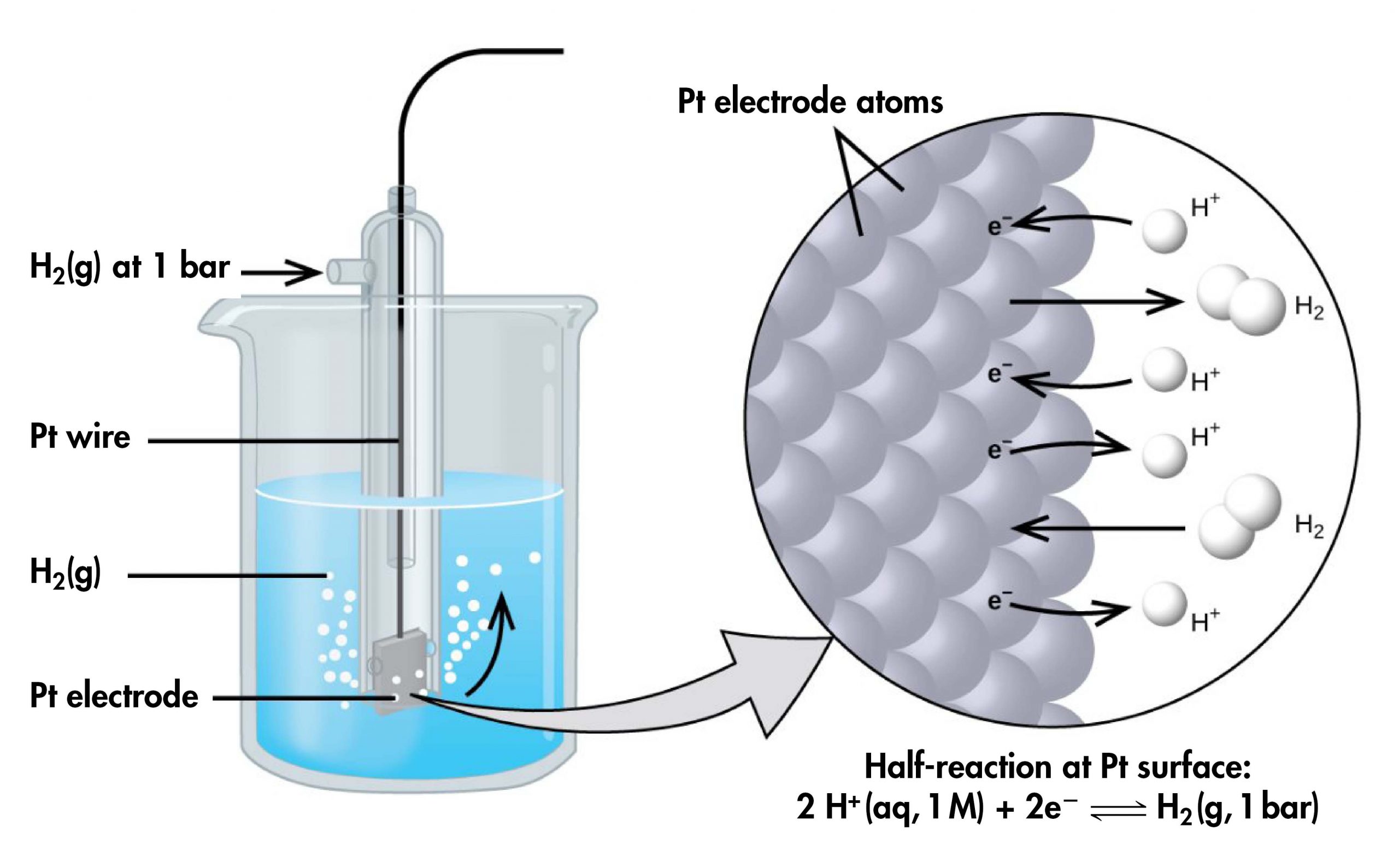
If a cell is set up with the SHE on the left and the half-cell whose potential we want to measure on the right, with all concentrations 1 M and all gas partial pressures 1 bar, then the reading on the voltmeter is E°, the standard half-cell potential, for the half-cell on the right. (Unless specified, the temperature is typically assumed to be 25 ºC.)
For example, a voltaic cell consisted of a SHE and a Cu2+ | Cu(s) half-cell can be used to determine the standard half-cell potential for Cu2+ | Cu(s).
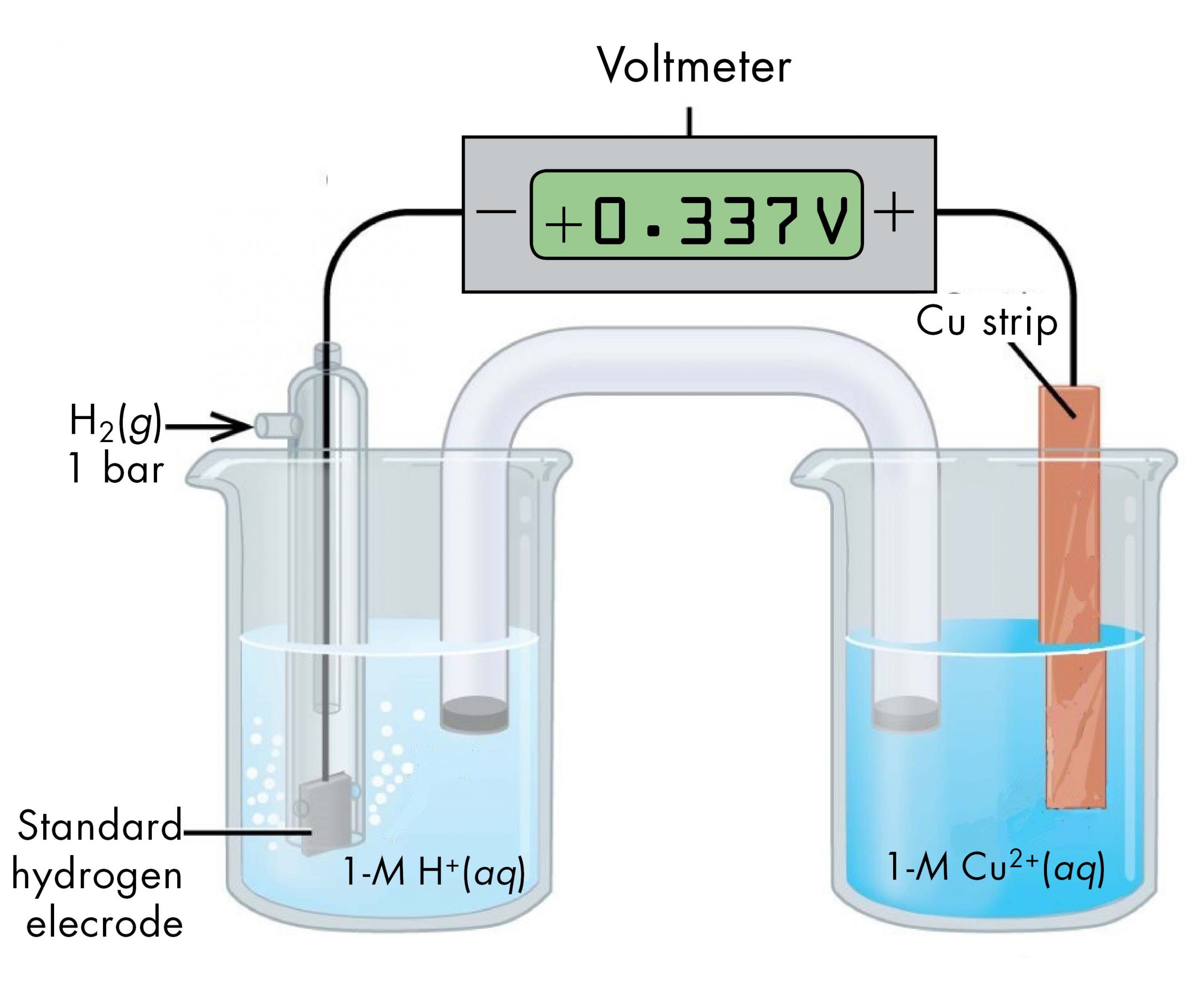
The cell notation for this voltaic cell is:
As we noted earlier, the cell potential, E°cell, measured by the voltmeter, is the difference between the potential of the right-hand half-cell and the left-hand half-cell:
From the measured E°cell = +0.337 V and the defined potential of zero for the Pt(s) | H2(g, 1 bar) | H+(aq, 1 M) half-cell, we can calculate E° of the Cu2+(aq, 1 M) | Cu(s) half-cell:
Sometimes, when a cell is set up with the SHE on the left, the reading on the voltmeter is negative. That is, for some half-cells the standard half-cell potential is lower than the potential for the Pt(s) | H2(g, 1 bar) | H+(aq, 1 M) half-cell. Consider the cell shown below, with cell notation:
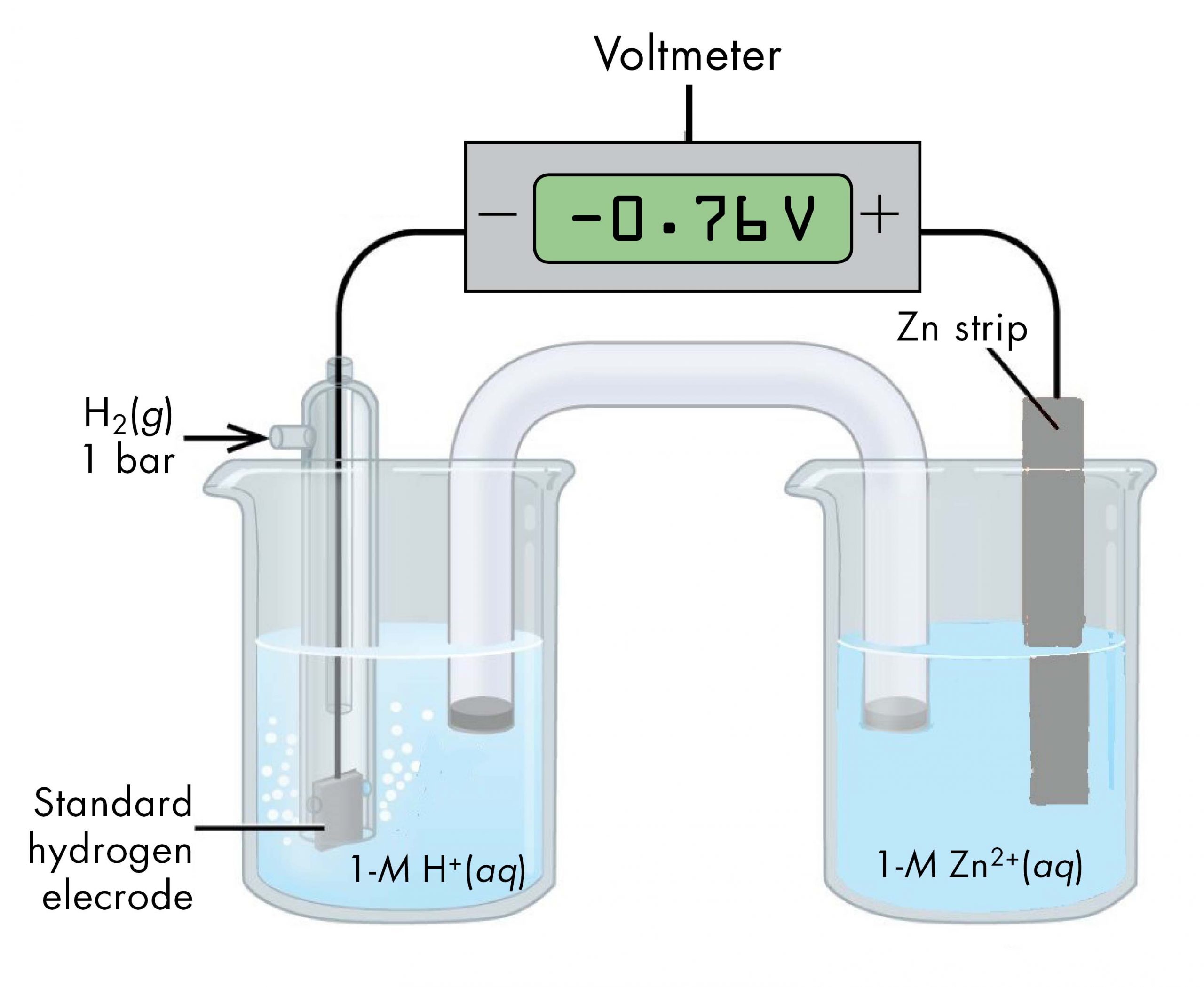
Following the same reasoning as for the Cu2+(aq, 1 M) | Cu(s) half-cell, E° of the Zn2+(aq, 1 M) | Zn(s) half-cell can be calculated.
It may seem strange that the standard half-cell potential is negative. This just reflects the fact that the electrical potential of the Zn2+(aq, 1 M) | Zn(s) half-cell is lower than the electrical potential of the Pt(s) | H2(g, 1 bar) | H+(aq, 1 M) half-cell.
The standard hydrogen electrode is rather dangerous because H2(g) is very flammable. Hence, it is rarely used in the laboratory. Its main significance is that it establishes the “zero” for standard half-cell potentials. Most standard half-cell potentials are measured by setting up a voltaic cell with one half-cell of known standard potential and one half-cell of unknown (to be measured) standard potential.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

