33 Defining a Buffer; Calculating the pH of a Buffer Solution (M16Q1)

Learning Objectives

  • Describe, recognize, and provide examples of buffer solutions; identify the components of buffer systems.
    | How Buffers Work |
  • Apply a Ka expression or the Henderson-Hasselbalch equation in order to calculate the pH of a buffer system.
    | Henderson-Hasselbalch Equation |

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Buffers

A buffer solution, or a buffer is a solution composed of approximately equal amounts of a dissolved weak acid and weak base conjugate pair. Buffer solutions resist a change in pH when a strong acid or a strong base are added (Figure 1).

A solution of acetic acid and acetate ion (CH3COOH + CH3COO–) is an example of an acidic buffer. A solution of ammonia and ammonium ion (NH3 + NH4+) is an example of a basic buffer. Both contain both weak acid and weak base, regardless of the resulting pH.

To summarize, both a weak acid and weak base must be present in a buffer solution, and the weak acid and weak base must be conjugate pairs.

Two images are shown. Image a on the left shows two beakers that each contain yellow solutions. The beaker on the left is labeled “Unbuffered” and the beaker on the right is labeled “p H equals 8.0 buffer.” Image b similarly shows 2 beakers. The beaker on the left contains a bright orange solution and is labeled “Unbuffered.” The beaker on the right is labeled “p H equals 8.0 buffer.”
Figure 1. (a) The buffered solution on the left and the unbuffered solution on the right have the same pH (pH 8); they are basic, showing the yellow color of the indicator methyl orange at this pH. (b) After the addition of 1 mL of a 0.01-M HCl solution, the buffered solution has not detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in color of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)

Chemistry in Real Life: Blood and Buffers

Blood is an important example of a buffered solution, with the principal acid and ion responsible for the buffering action being carbonic acid, H2CO3, and the bicarbonate ion, HCO3–.

H2CO3(aq)  +  H2O(l)   ⇌   HCO3–(aq)  +  H3O+(aq)

The pH of human blood remains very near 7.35, that is, slightly basic. Variations are usually less than 0.1 of a pH unit. A change of 0.4 of a pH unit is likely to be fatal.

How Buffers Work

A mixture of acetic acid and sodium acetate is a buffer because it contains both the weak acid and its conjugate base, assuming their quantities are similar. If we add a strong acid, the acetate ions will react with the hydronium ions created by the strong acid to produce acetic acid and water (as seen below). Acetic acid is a weak acid, which will cause the pH to decrease by a very small amount compared to the addition of a strong acid to pure water.

CH3COO–(aq)  +  H3O+(aq)  →   CH3COOH(aq)  +  H2O(l)

Conversely, if we add a strong base, such as sodium hydroxide, the hydroxide ions react with the acetic acid to produce acetate ions and water. Acetate ions are a weak base, which cause the pH to increase by a very small amount compared to the addition of a strong base to water.

CH3COOH(aq)  +  OH–(aq)  →   CH3COO–(aq)  +  H2O(l)

These two examples show how a buffer is able to resist pH changes even when a strong acid or base are added (Figure 2).

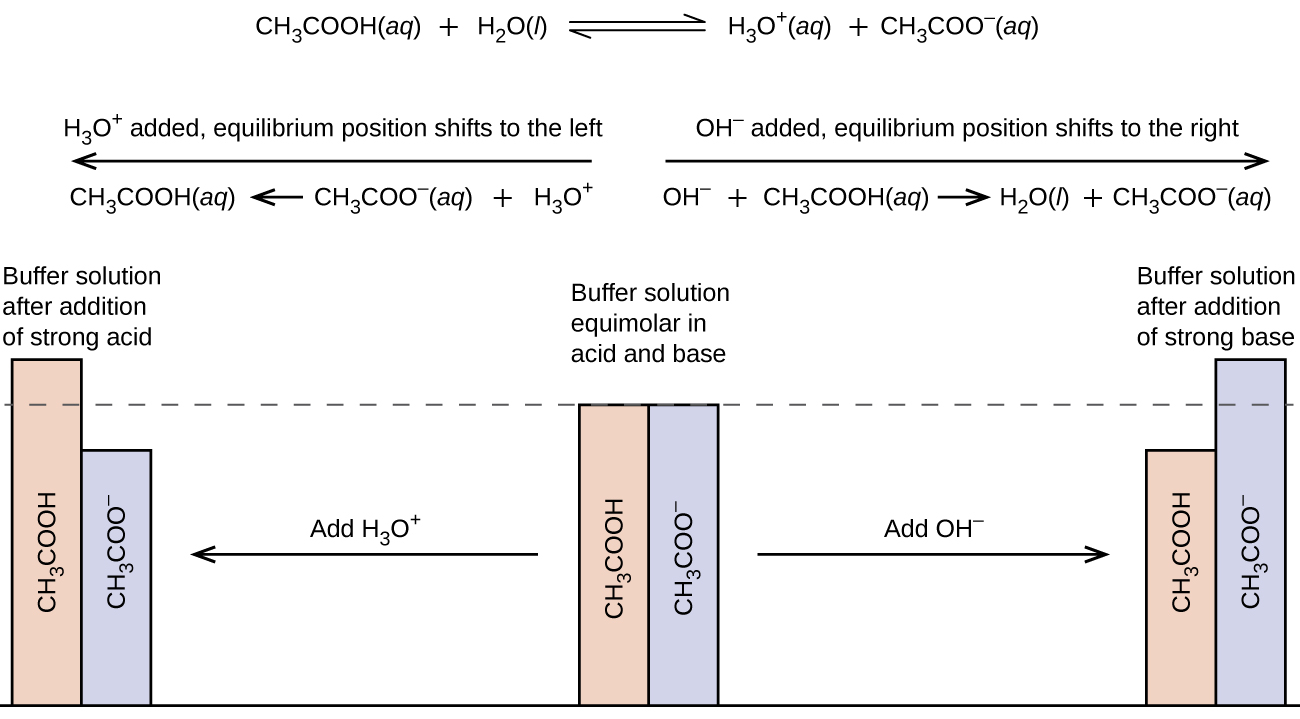
This figure begins with a chemical reaction at the top: C H subscript 3 C O O H ( a q ) plus H subscript 2 O ( l ) equilibrium arrow H subscript 3 O superscript positive sign ( a q ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below this equation are two arrows: one pointing left and other pointing right. The arrow pointing left has this phrase written above it, “H subscript 3 O superscript positive sign added, equilibrium position shifts to the left.” Below the arrow is the reaction: C H subscript 3 C O O H ( a q ) left-facing arrow C H subscript 3 C O O superscript negative sign ( a q ) plus H subscript 3 O superscript positive sign. The arrow pointing right has this phrase written above it, “O H subscript negative sign added, equilibrium position shifts to the right.” Below the arrow is the reaction: O H superscript negative sign plus C H subscript 3 C O O H ( a q ) right-facing arrow H subscript 2 O ( l ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below all the text is a figure that resembles a bar graph. In the middle are two bars of equal height. One is labeled, “C H subscript 3 C O O H,” and the other is labeled, “C H subscript 3 C O O superscript negative sign.” There is a dotted line at the same height of the bars which extends to the left and right. Above these two bars is the phrase, “Buffer solution equimolar in acid and base.” There is an arrow pointing to the right which is labeled, “Add O H superscript negative sign.” The arrow points to two bars again, but this time the C H subscript 3 C O O H bar is shorter than that C H subscript 3 C O O superscript negative sign bar. Above these two bars is the phrase, “Buffer solution after addition of strong base.” From the middle bars again, there is an arrow that points left. The arrow is labeled, “Add H subscript 3 O superscript positive sign.” This arrow points to two bars again, but this time the C H subscript 3 C O O H bar is taller than the C H subscript 3 C O O superscript negative sign bar. These two bars are labeled, “Buffer solution after addition of strong acid.”
Figure 2. This diagram shows the buffer action of these reactions.

A mixture of ammonia and ammonium chloride is basic because the Kb for ammonia is greater than the Ka for the ammonium ion. It is a buffer because it also contains a weak acid and a weak base, assuming their quantities are close to equal. If we add a strong acid, the ammonia molecules will react with the hydronium ions to produce ammonium and water (as seen below), converting a strong acid into a weak acid.

NH3(aq)  +  H3O+(aq)  →   NH4+(aq)  +  H2O(l)

If we add a strong base, the ammonium ions will react with the hydroxide ions to produce ammonia and water (as seen below), converting a strong base into a weak base.

NH4+(aq)  +  OH–(aq)   →   NH3(aq)  +  H2O(l)

The Henderson-Hasselbalch Equation

The Henderson-Hasselbalch equation is used to calculate the pH of buffer solutions from the ionization constant (Ka) of the relevant weak acid and the concentrations of both the weak acid and its conjugate base in solution. This equation is derived from the equilibrium expression for a weak acid dissociating in water, as can be seen below.

The ionization-constant expression for a solution of a weak acid can be written as:

Ka = [latex]\frac{[H_{3}O^{+}][A^{-}]}{[HA]}[/latex]

After rearranging to solve for [H3O+]:

[H3O+] = Ka × [latex]\frac{[HA]}{[A^{-}]}[/latex]

Taking the negative logarithm of both sides of this equation:

– log[H3O+] = – log Ka – log[latex]\frac{[HA]}{[A^{-}]}[/latex],

which can be written as

pH = pKa + log[latex]\frac{[A^{-}]}{[HA]}[/latex]

where pKa is the negative of the common logarithm of the ionization constant of the weak acid (pKa = −log Ka). The Henderson-Hasselbalch equation always uses the Ka of the conjugate acid/base pair.

Example 1

Calculating the pH of Buffer Solutions
Calculate the pH of an acetic acid buffer solution with a Ka = 1.8 x 10-5, [CH3COONa] = 0.25 M and [CH3COOH] = 0.50 M.

Solution

Using the given Ka and concentrations, plug all the values into the Henderson-Hasselbalch equation:

pH = pKa + log[latex]\frac{[A^{-}]}{[HA]}[/latex]

pH = -log 1.8 × 10-5 + log [latex]\frac{[0.25]}{[0.50]}[/latex]

pH = 4.74 – 0.301

pH = 4.44

Check Your Learning
Calculate the pH of an ammonia buffer solution with a Kb of 1.8 x 10-5, [NH3] = 0.70 M and [NH4+] = 0.40 M.

Answer:

pH = 9.49 (Hint: Don’t forget to calculate the Ka!)

Chemistry in Real Life: Lawrence Joseph Henderson and Karl Albert Hasselbalch

Lawrence Joseph Henderson (1878–1942) was an American physician, biochemist and physiologist, to name only a few of his many pursuits. He obtained a medical degree from Harvard and then spent 2 years studying in Strasbourg, then a part of Germany, before returning to take a lecturer position at Harvard. He eventually became a professor at Harvard and worked there his entire life. He discovered that the acid-base balance in human blood is regulated by a buffer system formed by the dissolved carbon dioxide in blood. He wrote an equation in 1908 to describe the carbonic acid-carbonate buffer system in blood. Henderson was broadly knowledgeable; in addition to his important research on the physiology of blood, he also wrote on the adaptations of organisms and their fit with their environments, on sociology and on university education. He also founded the Fatigue Laboratory, at the Harvard Business School, which examined human physiology with specific focus on work in industry, exercise, and nutrition.

In 1916, Karl Albert Hasselbalch (1874–1962), a Danish physician and chemist, shared authorship in a paper with Christian Bohr in 1904 that described the Bohr effect, which showed that the ability of hemoglobin in the blood to bind with oxygen was inversely related to the acidity of the blood and the concentration of carbon dioxide. The pH scale was introduced in 1909 by another Dane, Sørensen, and in 1912, Hasselbalch published measurements of the pH of blood. In 1916, Hasselbalch expressed Henderson’s equation in logarithmic terms, consistent with the logarithmic scale of pH, and the Henderson-Hasselbalch equation was born.

Key Concepts and Summary

Buffer solutions, which contain a conjugate weak acid and weak base pair, resist a change in pH when a strong acid or a strong base are added. When a strong acid is added, the weak base reacts converting the strong acid into a weak acid (resulting in a small pH decrease). When a strong base is added, the weak acid reacts converting the strong base into a weak base (resulting in a small pH increase).

The Henderson-Hasselbalch equation can be used to calculate the pH of a buffer solution, both before and after a strong acid or strong base addition. This equation is: pH = pKa + log [latex]\frac{[A^{-}]}{[HA]}[/latex], where pH = -log[H3O+], pKa = -log(Ka), [A–] = moles or concentration of the weak base, [HA] = moles or concentration of the weak acid.

Key Equations

  • pH = pKa + log [latex]\frac{[A^{-}]}{[HA]}[/latex]

Glossary

buffer
solution composed of approximately equal amounts of a dissolved weak acid and weak base conjugate pair
Henderson-Hasselbalch equation
used to calculate the pH of buffer solutions from the ionization constant (Ka) and the concentrations of both the weak acid and its conjugate base in solution.

Chemistry End of Section Exercises

  1. What is a buffer?
  2. Write the chemical equation that represents a buffer comprised of equal amounts of the acid H3PO4 and a salt of its conjugate base NaH2PO4. Explain why the pH does not change significantly when a small amount of (a) an acid or (b) a base is added to this solution.
  3. Write the chemical equation that represents a buffer comprised of equal amounts of the base NH3 and a salt of its conjugate acid NH4Cl. Explain why the pH does not change significantly when a small amount of (a) an acid or (b) a base is added to this solution.
  4. Which of the following combinations could be used to create a buffer solution?
    1. HNO3 and HNO2
    2. HNO2 and NO3–
    3. NO2– and HNO2
    4. NH4+ and NH3
    5. NH3 and CH3NH2
  5. What is the effect (increase, decrease, no effect) on the concentration of formic acid (HCOOH), hydronium ion, and formate ion (HCOO–) when the following are added to a buffer solution of equal concentrations of formic acid and sodium formate:
    1. HCl
    2. KHCOO
    3. NaCl
    4. KOH
    5. HCOOH
  6. What is the effect (increase, decrease, no effect) on the pH when the following are added to a buffer solution of equal concentrations of NaH2PO4 and Na2HPO4:
    1. HCl
    2. K2HPO4
    3. NaCl
    4. KOH
    5. NaH2PO4
  7. What is the pH of a solution that is 0.25 M CH3COOH and 0.030 M NaCH3COO. The Ka for CH3COOH is 1.8 × 10-5.
  8. What is the pH of a solution that is 0.075 M HNO2 and 0.030 M NaNO2. The Ka for HNO2 is 7.4 × 10-4.
  9. What is the pH of a buffer that is 0.125 M CH3NH2 and 0.130 M CH3NH3Cl. The Kb for CH3NH2 is 5.0 × 10-4.
  10. What is the pH of a buffer that is 1.25 M NH3 and 0.78 M NH4Cl. The Kb for NH3 is 1.77 × 10-5,

Answers to Chemistry End of Section Exercises

  1. A buffer is a solution that resists change in pH when small amounts of a strong acid or base are added. The solution is comprised of approximately equal concentrations of a weak acid and its conjugate base (or a weak base and its conjugate acid).
  2. H3PO4(aq) + H2O(l) ⇌ H2PO4–(aq) + H3O+(aq); Note that the Na+ is a spectator ion and is not included
    (a) Added acid, H3O+, is removed primarily by reacting with the base, H2PO4–, shown in following equation:
    H3O+(aq) + H2PO4–(aq) → H3PO4(aq) + H2O(l)
    (b) Added base, OH–, is removed primarily by reacting with the acid, H3PO4, by the reaction:
    OH–(aq) + H3PO4(aq) → H2PO4–(aq) + H2O(l)
  3. NH4+(aq) + H2O(l) ⇌ NH3(aq) + H3O+(aq); Note that the Cl– is a spectator ion and is not included
    (a) Added acid, H3O+, is removed primarily by reacting with the base, NH3, shown in following equation:
    H3O+(aq) + NH3(aq) → NH4+(aq) + H2O(l)
    (b) Added base, OH–, is removed primarily by reacting with the acid, NH4+, by the reaction:
    OH–(aq) + NH4+(aq) → NH3(aq) + H2O(l)
  4. Buffers are mixtures of a weak acid and its conjugate base. (c) and (d)
  5. Buffer reaction: HCOOH(aq) + H2O(l) ⇌ HCOO–(aq) + H3O+(aq)
    Consider the effects using Le Châtelier’s Principle:

    1. HCl adds H3O+ to the reaction, pushing the equilibrium toward the reactants. This causes [HCOOH] to increase, [H3O+] to increase, and [HCOO–] to decrease.
    2. KHCOO is a soluble ionic compound and will dissolve upon addition to the solution. The K+ is a spectator ion and will not affect the equilibrium. Additional HCOO– will shift the equilibrium toward the reactants, causing the [HCOOH] to increase, [H3O+] to decrease, and [HCOO–] to increase.
    3. NaCl will dissolve, adding Na+ and Cl– ions to the solution. Neither of these will effect the equilibrium and so the concentrations will be unchanged.
    4. KOH will dissolve upon addition, adding K+ and OH– ions to the solution. The OH- ions will react with the H3O+, decreasing the H3O+ concentration and causing the equilibrium to shift to toward the products. The [HCOOH] will decrease, [H3O+] will decrease, and [HCOO–] will increase.
    5. Adding HCOOH will shift the equilibrium toward the products. The [HCOOH] will decrease, [H3O+] will increase, and [HCOO–] will increase.
  6. Buffer reaction: H2PO4–(aq) + H2O(l) ⇌ HPO42-(aq) + H3O+(aq)
    1. pH will decrease
    2. pH will increase
    3. pH will be unchanged.
    4. pH will increase.
    5. pH will decrease
  7. 3.82
  8. 2.73
  9. 10.68
  10. 9.45

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

CHEM 104: Working Copy Copyright © by Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book

Feedback/Errata

1 Responses to Defining a Buffer; Calculating the pH of a Buffer Solution (M16Q1)

Leave a Reply

Your email address will not be published. Required fields are marked *