17 Mechanisms and Multistep Reactions; Reaction Profiles; Rate Limiting Steps (M13Q10)

Learning Objectives

  • Identify characteristics and components of mechanisms, such as elementary steps and their rate laws, the rate-determining step, and intermediates.
  • Critique a provided reaction mechanism by determining whether it is in agreement with the experimentally determined stoichiometry of a reaction and the experimentally determined rate law.
  • Sketch a reaction profile based on a provided mechanism, or critique a mechanism based on a provided reaction profile.

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Relating Reaction Mechanisms to Rate Laws

It’s often the case that one step in a multistep reaction mechanism is significantly slower than the others. Because a reaction cannot proceed faster than its slowest step, this step will limit the rate at which the overall reaction occurs. The slowest step is therefore called the rate-determining step (or rate-limiting step) of the reaction.

A photo is shown of cattle passing through a narrow chute into a holding pen. A person directs them through the gate with a long white and red pole.
Figure 1. A cattle chute is a nonchemical example of a rate-determining step. Cattle can only be moved from one holding pen to another as quickly as one animal can make its way through the chute. (credit: Loren Kerns)

Deriving a Rate Law from a Multi-step Mechanism with a Slow First Step

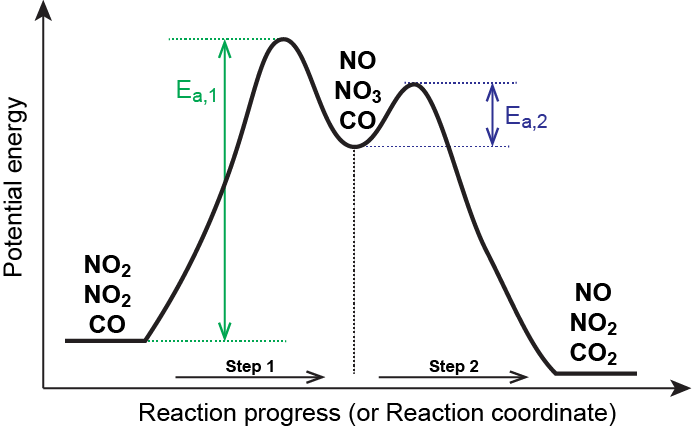
As described earlier, rate laws may be derived directly from the chemical equations for elementary reactions. We cannot assume this to be true for overall balanced equations because they often represent the overall change for a chemical system, and very often are the result of a multistep reaction mechanisms. Overall rate laws must be determined from experimental data and the mechanism deduced from the rate law (and sometimes from other data). The reaction of NO2 and CO provides an illustrative example:

NO2(g)  +  CO(g)  →  CO2(g)  +  NO(g)

At temperatures below 225 °C, the reaction is described by a rate law that is second order with respect to NO2:

rate = k[NO2]2

This is consistent with a mechanism that involves the following two elementary reactions, the first of which is slower and is therefore the rate-determining step:

Step 1 NO2(g)  +  NO2(g)  →  NO3(g)  +  NO(g) slow
Step 2 NO3(g)  +  CO(g)  →  NO2(g)  +  CO2(g) fast

The rate-determining step gives a rate law showing second-order dependence on the NO2 concentration, and the sum of the two equations gives the net overall reaction. In this mechanism, NO3 is an intermediate.

In general, when the rate-determining (slower) step is the first step in a mechanism, the rate law for the overall reaction is the same as the rate law for this step.

In a reaction coordinate diagram, each step in a multi-step mechanism will have its own activation energy, resulting in an energy peak for each step. The rate-determining, or slow, step will have the largest activation energy. This can be seen in Figure 2 below.

Figure 2. Reaction coordinate diagram for the reaction: NO2(g) + CO(g) → CO2(g) + NO(g). The sum of the two elementary reaction steps gives the net overall reaction—the NO3 that is formed in step (1) is consumed in step (2), and one of the NO2 consumed in step (1) is reformed in step (2).

Deriving a Rate Law from a Multi-step Mechanism with a Fast (Equilibrium) First Step

When the rate-determining step is preceded by a step involving an equilibrium reaction, the rate law for the overall reaction may be more difficult to derive. The following general mechanism example will illustrate how to derive overall rate laws from mechanisms involving equilibrium steps preceding the rate-determining step.

Consider the following general mechanism:

Step 1 A   +   B   ⇌   C Fast equilibrium
Step 2 C  +  B     →   2 D Slow
Overall A   +   2 B   →   2 D

The rate law is determined by the slow step and would be:

rate  =  k2[B][C]

where k2 is the rate constant for the second step in the mechanism. However, this rate law contains an intermediate and intermediates cannot be included in the overall rate law expression, since their concentrations cannot usually be measured. To replace the intermediate, it is possible to use step 1, the fast equilibrium, to derive the overall rate law using a technique that is referred to as the steady state approximation.

In an equilibrium reaction, the rate of the forward reaction equals the rate of the reverse reaction. Thus, for a general reaction like A  +  B   ⇌   C

Forward reaction A   +   B   →   C rateforward  =  k1[A][B], where k1 is the rate constant for the forward reaction
Reverse reaction C   →   A   +   B ratereverse  =  k-1[C], where k-1 is the rate constant for the reverse reaction

Because the rates are equal, this can be summarized as:

rateforward =  ratereverse

or

k1[A][B]  =  k-1[C]

[C] can be isolated using algebra and substituted into the rate law, resulting in an rate law that contains only reactants:

[C]  =  [latex]\frac{k_{1}[A][B]}{k_{-1}}[/latex]

rate  =  k2[B][C] = k2[B][latex](\frac{k_{1}[A][B]}{k_{-1}})[/latex] = [latex]\frac{k_{2}k_{1}}{k_{-1}}[/latex][A][B]2
The rate constants are usually condensed into a single overall k. The overall  rate law can be then written as:
rate  =  k[A][B]2
The reaction coordinate for this reaction is given in Figure 3. Notice that there is a separate activation energy peak for each step and that the larger activation energy corresponds to the slow step in the mechanism.
Figure 3. A reaction coordinate diagram for a mechanism with a fast equilibrium first step and a slow, rate-determining, second step.

Example 1

Deriving the Overall Rate Law Expression for a Multistep Reaction Mechanism

Atomic oxygen in the atmosphere reacts with ozone in the following pair of elementary reactions:

Step 1 Cl(g)  +  O3(g)  ⇌  ClO(g)  +  O2(g) fast equilibrium
Step 2 ClO(g)  +  O(g)  →  Cl(g)  +  O2(g) slow

Determine the overall reaction, identify any intermediates, and determine the overall rate law expression.

1.  Add the two steps together. Cancel out species found on both the reactant and product sides to find the overall reaction:

Cl(g)  +  O3(g)  ⇌  ClO(g)  +  O2(g)
+ ClO(g)  +  O(g)  →  Cl(g)  +  O2(g)
Overall reaction: O3(g)  +  O(g)  →  2O2(g)

2.  Intermediates are formed in one step and then used in a subsequent step. They do not appear in the overall reaction:

OCl is an intermediate. It is formed in step 1 and then used in step 2 – it does not appear in the final overall reaction.

Note: Cl is a catalyst, not an intermediate. It is present in the beginning and used in step 1. It is reformed in step 2. It does not appear in the final overall reaction. We will learn more about catalysts in the next section.

3.  Determine the overall rate law:

The rate law from the slow or rate-determining step is:

rate  =  k2[ClO][O]

This contains an intermediate and therefore is not a valid overall rate law. Find [OCl] in terms of reactants found in the overall reaction equation.

rateforward  =  ratereverse

k1[Cl][O3]  =  k-1[ClO][O2]

[ClO]  =  [latex]\frac{k_{1}[Cl][O_{3}]}{k_{-1}[O_{2}]}[/latex]

Substitute this into the rate-determining rate law:

rate  =  k2[ClO][O] = k2[latex]( \frac{k_{1}[Cl][O_{3}]}{k_{-1}[O_{2}]} )[/latex][O]

Simplified:

rate = k[latex]\frac{[Cl][O_{3}][O]}{[O_{2}]}[/latex]

where:

k  =  [latex]\frac{k_{1}k_{2}}{k_{-1}}[/latex]

Note: While it is not always the case, catalysts and products can be in the rate law. It is also possible to have negative orders, where the presence of a species in the reaction will slow down the reaction rate as its concentration increases.

Key Concepts and Summary

To determine a rate law for an overall reaction, either experimental evidence or a valid mechanism must be used, not the coefficients of the overall reaction. To use a mechanism to determine the rate law, identify the slow step of the reaction, which is either labeled “slow” or has the highest activation energy. This slow step is known as the rate-determining step, since its completion limits the entire reaction’s rate of completion. Then, a rate law can be written using the reactants and coefficients from the rate-determining step. If this rate law happens to have an intermediate, then the steady-state approximation must be employed to replace the intermediate, since measuring the concentration of an intermediate is extremely difficult.

Key Equations

  • rateforward =  ratereverse

Glossary

rate-determining step
the slowest step in a reaction mechanism

steady-state approximation
a technique used to replace an intermediate in a rate law derived from the slowest step

Chemistry End of Section Exercises

  1. Compound A reacts with compound B, according to the following equation:

    2 A(g) + 2 B(g) → C(g) + 2 D(l)

    What would the rate law be if the mechanism for this reaction were:

    2 A(g) + B(g) → C(g) + E(l) Slow
    E(l) + B(g) → 2 D(l) Fast
  2. Experiments were conducted to study the rate of the reaction represented by this equation.[1]

    2 NO(g) + 2 H2(g) → N2(g) + H2O(g)

    Initial concentrations and rates of reaction are given here:

    Experiment Initial Concentration [NO] (M) Initial Concentration, [H2] (M) Initial Rate of Formation of N2 (M/min)
    1 0.0060 0.0010 1.8 × 10−4
    2 0.0060 0.0020 3.6 × 10−4
    3 0.0010 0.0060 0.30 × 10−4
    4 0.0020 0.0060 1.2 × 10−4

    Consider the following questions:

    1. Determine the order for each of the reactants, NO and H2, from the data given and show your reasoning.
    2. Write the overall rate law for the reaction.
    3. Calculate the value of the rate constant, k, for the reaction. Include units.
    4. The following sequence of elementary steps is a proposed mechanism for the reaction:
      NO(g) + NO(g) → N2O2(g)
      N2O2(g) + H2(g) → H2O(l) + N2O(g)
      N2O(g) + H2(g) → N2(g) + H2O(l)

      Based on the data presented, which of these is the rate determining step? Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.

  3. The reaction of CO with Cl2 gives phosgene (COCl2), a nerve gas that was used in World War I. Use the mechanism shown here to complete the following exercises:
    Mechanism Step Rate Constant
    Cl2(g) ⇌ 2 Cl(g) fast k1 is the rate constant for the forward reaction and k-1 is the rate constant for the reverse reaction
    CO(g) + Cl(g) → COCl(g) slow k2
    COCl(g) + Cl(g) ⇌ COCl2(g) fast k3 is the rate constant for the forward reaction and k-3 is the rate constant for the reverse reaction
    1. Write the overall reaction.
    2. Identify all intermediates.
    3. Write the rate law for each elementary reaction.
    4. Write the overall rate law expression.

Answers to Chemistry End of Section Exercises

  1. rate = k[A]2[B]
    1. Doubling [H2] doubles the rate. [H2] must enter the rate equation to the first power. Doubling [NO] increases the rate by a factor of 4. [NO] must enter the rate law to the second power.
    2. Rate = k[NO]2[H2]
    3. k = 5.0 × 103 M−2 min−1
    4. The three reactions do add up to the overall reaction so the mechanism is a plausible scenario. Using the following logic, the mechanism would be fast-slow-fast: If the first step was the rate determining (slow) step, the rate law would be rate = k[NO]2. This disagrees with the experimentally determined rate law so it cannot be the rate determining step. If the second step is the rate determining step, then the rate law would be rate = k[NO]2[H2]. This agrees with the experimentally determined rate law so it is likely that the second step is the rate determining step. Since the rate determining step is the slowest step, the third step would have to be a fast step.
    1. Cl2(g) + CO(g) → COCl2(g)
    2. Cl, COCl
    3. rate = k1[Cl2]; rate = k2[CO][Cl]; rate = k3[COCl][Cl]
    4. rate = k[CO][Cl2]½; k = k1½k2/k-1½

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

CHEM 104: Working Copy Copyright © by Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book

Feedback/Errata

Leave a Reply

Your email address will not be published. Required fields are marked *