38 Titration of a Weak Acid with a Strong Base; Titration of a Weak Base with a Strong Acid (M16Q6)
Learning Objectives
- Identify key species present in the titration of a weak acid by a strong base (or a weak base by a strong acid).
- Determine pH and concentrations of chemical species at any point in the titration of a weak acid by a strong base or a weak base by a strong acid.
| Titrations Flow Chart | - Determine the Ka or Kb value for a weak acid or weak base from a given titration curve, as well as the equivalence point for the titration.
The titration of a weak acid with a strong base (or of a weak base with a strong acid) follows the same general principle as those discussed for a strong acid/strong base titration but typically has an extra step or two in the calculations. Let us consider the titration of 25.0 mL of 0.100 M acetic acid (a weak acid) with 0.100 M sodium hydroxide and compare the titration curve with that of the strong acid (Figure 1).
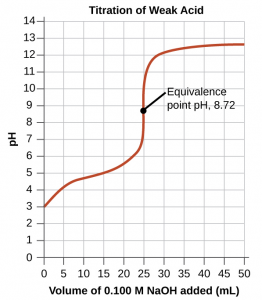
Although the initial volume and molarity of the acids are the same, there are important differences between the two titration curves. The titration curve for the weak acid begins at a higher value (less acidic) and maintains higher pH values up to the equivalence point. The pH at the equivalence point is also higher (8.72 rather than 7.00) due to the presence of the acetate ion and water at the equivalence point:
After the equivalence point, the two curves are identical because the pH is only dependent on the excess hydroxide added in both cases.
Example 1
Titration of a Weak Acid with a Strong Base
The titration curve shown in Figure 1 is for the titration of 25.00 mL of 0.100 M CH3COOH with 0.100 M NaOH. The reaction can be represented as:
(a) What is the initial pH before any amount of the NaOH solution has been added? Ka = 1.8 × 10−5 for CH3COOH.
(b) Find the pH after 12.50 mL of the NaOH solution have been added.
(c) Find the pH after 25.00 mL of the NaOH solution has been added.
(d) Find the pH after 37.50 mL of the NaOH solution has been added.
Solution
(a) Since there is only a weak acid in solution, we can use an ICE table to aid is in calculating the pH:
| CH3COOH(aq) + H2O(l) ⇌ CH3COO-(aq) + H3O+(aq) | ||||
| I (Intial) | 0.100 | - | 0 | 0 |
| C (Change) | -x | - | + x | + x |
| E (Equilibrium) | 0.100 - x | - | x | x |
Assuming that the dissociated amount is small compared to 0.100 M, we find that:
Ka = [latex]\frac{[H_{3}O^{+}][CH_{3}COO^{-}]}{[CH_{3}COOH]} = \frac{x^{2}}{[0.100 - x]} = \frac{x^{2}}{[0.100]}[/latex] = 1.8 × 10-5
x = [latex]\sqrt{1.8 \times 10^{-5} \times 0.100}[/latex]
x = 1.3 × 10-3
pH = -log[H3O+] = -log(1.3 × 10-3) = 2.87
(b) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:
moles CH3COOH = 25.00 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1\ L}[/latex] = 0.002500 moles CH3COOH
moles OH- = 12.50 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1\ L}[/latex] = 0.001250 moles OH-
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.001250 | 0 | - |
| C (Change) | - | |||
| F (Finish) | - | |||
Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero.
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.001250 | 0 | - |
| C (Change) | -0.001250 | -0.001250 | +0.001250 | - |
| F (Finish) | 0.001250 | 0 | 0.001250 | - |
The last step is to ask ourselves "What's left in the beaker?" We have the conjugate acid/base pair left in the beaker, so we can use the Henderson-Hasselbalch equation to solve for the pH.
pH = pKa + log [latex]\frac{[base]}{[acid]}[/latex]
pH = -log(1.8 × 10-5) + log [latex]\frac{[0.001250]}{[0.001250]}[/latex]
pH = 4.74
Notice that the pH is equal to the pKa. We could have predicted this since the moles of conjugate base are equal to the moles of acid! This represents the half-equivalence point of the titration.
(c) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:
moles CH3COOH = 25.00 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1\ L}[/latex] = 0.002500 moles CH3COOH
moles OH- = 25.00 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1\ L}[/latex] = 0.002500 moles OH-
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.002500 | 0 | - |
| C (Change) | - | |||
| F (Finish) | - | |||
Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero.
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.002500 | 0 | - |
| C (Change) | -0.002500 | -0.002500 | +0.002500 | - |
| F (Finish) | 0 | 0 | 0.002500 | - |
The last step is to ask ourselves "What's left in the beaker?" We have only the conjugate base and water left in solution (a weak base solution). In order to solve for the pH of a weak base, we first need to flip the reaction, set up an ICE table, and calculate the new concentration of the conjugate base, and set up a Kb expression.
[CH3COO-] = [latex]\frac{0.002500\ moles}{0.05000\ L}[/latex] = 0.0500 M CH3COO-
| CH3COO-(aq) + H2O(l) ⇌ CH3COOH(aq) + OH-(aq) | ||||
| I (Initial) | 0.0500 | - | 0 | 0 |
| C (Change) | - x | - | + x | + x |
| E (Equilibrium) | 0.0500 - x | - | x | x |
Kb = [latex]\frac{K_{w}}{K_{a}} = \frac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}}[/latex] = 5.6 × 10-10
Kb = [latex]\frac{[OH^{-}][CH_{3}COOH]}{[CH_{3}COO^{-}]} = \frac{x^{2}}{[0.0500 - x]} = \frac{x^{2}}{[0.0500]}[/latex] = 5.6 × 10-10
x = [latex]\sqrt{5.6 \times 10^{-10} \times 0.0500}[/latex]
x = 5.3 × 10-6
pOH = -log[OH-] = -log(5.3 × 10-6) = 5.28
pH = 14.00 - pOH = 14.00 - 5.28 = 8.72
Note that the pH at the equivalence point of this titration is significantly greater than 7 since only the weak base remains at the equivalence point!
(d) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:
moles CH3COOH = 25.00 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1\ L}[/latex] = 0.002500 moles CH3COOH
moles OH- = 37.50 mL × [latex]\frac{1\ L}{1000\ mL} \times \frac{0.100\ moles\ CH_{3}COOH}{1 L}[/latex] = 0.003750 moles OH-
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.003750 | 0 | - |
| C (Change) | - | |||
| F (Finish) | - | |||
Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero.
| CH3COOH(aq) + OH-(aq) → CH3COO-(aq) + H2O(l) | ||||
| S (Start) | 0.002500 | 0.003750 | 0 | - |
| C (Change) | -0.002500 | -0.002500 | +0.002500 | - |
| F (Finish) | 0 | 0.001250 | 0.002500 | - |
The last step is to ask ourselves "What's left in the beaker?" We have both excess strong base and the conjugate weak base. We can use a very accurate approximation here to make solving for the pH much easier. The excess strong base will affect the pH much, MUCH more than the leftover conjugate weak base. So we will approximate the pH by the strong base alone by first calculating the concentration of the [OH-].
[OH-] = [latex]\frac{0.001250\ moles\ OH^{-}}{0.06250\ L}[/latex] = 0.0200 M OH-
pOH = -log[OH-] = -log(0.0200) = 1.70
pH = 14.00 - pOH = 14.00 - 1.70 = 12.30
Note that this result is the same as for the strong acid-strong base titration example provided earlier in this chapter, since the amount of the strong base added moves the solution past the equivalence point.
Check Your Learning
Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL. (Ka HCOOC is 3.0 × 10-4)
Answer:
0.00 mL, pH = 2.26; 15.0 mL, pH = 3.70; 25.00 mL, pH= 8.17; 30.0 mL, pH = 12.097
Flow Chart for Acid & Base Problems
Solving for concentrations and pH values in acid/base reactions can seem confusing how to approach at first. However, there are four primary scenarios that you will encounter, shown in Figure 1 below.
- The first scenario is in green, when you only have a weak acid or a weak base in water. We encounter these problems earlier this semester when studying acids and bases. Since both reactants are weak and do not dissociate 100%, the first step will be to write out the correct reaction and set up an ICE table.
- The second scenario is in red, when you only have a strong acid or a strong base in water. We also encountered these types of problems earlier this semester when studying acids and bases.
- The third scenario is in blue, when you have both an acid and a base reacting and one or both of them is strong. These are a typical titration problem and will require the most work of the four scenarios as there is always a second step to finish the problem.
- Once you have fully reacted the acid and base, you must look at "F" in your SCF table to determine what is left in your beaker. There are three possible outcomes, which just happen to be the three other scenarios in the flow chart!
- If you only have a weak acid or base with water left (which occurs in weak/strong titrations at the equivalence point), you must calculate the concentration of the remaining weak acid or base (by dividing by total volume), set up an ICE table, and use the appropriate equilibrium constant K.
- If you only have a strong acid or base left (which occurs often in a strong/strong titration or after the equivalence point in a weak/strong titration), you must calculate the concentration of the remaining strong acid or base (by dividing by total volume).
- If you have a buffer remaining (the weak conjugate acid/base pair, which occurs often before the equivalence point in a weak/strong titration), you can plug the moles directly into the Henderson-Hasselbalch equation, assuming everything is in the same beaker.
- Once you have fully reacted the acid and base, you must look at "F" in your SCF table to determine what is left in your beaker. There are three possible outcomes, which just happen to be the three other scenarios in the flow chart!
- The fourth scenario is in purple, when you have a weak acid-base pair that are also conjugates of each other. This is a buffer solution and you can use the Henderson-Hasselbalch equation to solve the problem.
![This figure contains a flow chart, beginning with a black box with the text “What’s in my beaker?” There are four arrows going from this black box. To the left is a green arrow pointing towards a green box with the text “only weak acid or base + H 2 O, I C E Table, (Need K a or K b)”. Pointing down to the left is a red arrow to a red box with the text “only strong acid or base, p H = - log [H 3 O +] or p O H”. Pointing down to the right is a blue arrow to a blue box with the text “acid and base, (one or both strong), balanced reaction, S C F Table, What’s left?”. Pointing to the right is a purple arrow to a purple box that says “acid and base, (both weak & conjugate pair), buffer, Find p H using Henderson-Hasselbalch Equation”. Pointing down from the blue box are three more arrows. A red arrow points to the left to the red box with “Divide by Total Volume” above the arrow. A green arrow points to the left to the green box with “Divide by Total Volume, Flip Reaction” above the arrow. The purple arrow points to the right to the purple box.](https://wisc.pb.unizin.org/app/uploads/sites/418/2019/08/104_M5Q5_titrationflowchart-1-1024x383.png)
Chemistry End of Section Exercises
- In a general chemistry lab session, 50.0 mL 1.00 M HNO2 is titrated with 0.500 M NaOH. (The Ka of HNO2 is 7.41 × 10-4)
- Write the net ionic equation for the titration reaction that occurs when 50.0 mL of 1.00 M HNO2 is titrated with 0.500 M NaOH.
- Are there spectator ions present? If so, what are they and how will they affect the pH?
- How many moles of NaOH will be added to the analyte to reach the equivalence point?
- How many mL of NaOH will be added to the analyte to reach the equivalence point?
- What is the pH at the equivalence point?
- In a general chemistry lab session, 100.0 mL of 1.00 M NH3 is titrated with 0.600 M HCl.
- Write the net ionic equation for the titration reaction that occurs when 100.0 mL 1.00 M NH3 is titrated with 0.600 M HCl.
- Are there spectator ions present? If so, what are they and how will they affect the pH?
- How many moles of HCl will be added to the analyte to reach the equivalence point?
- How many mL of HCl will be added to the analyte to reach the equivalence point?
- What is the pH at the equivalence point?
- 60.0 mL of a 0.050 M CH3COOH solution is titrated with a 0.075 M NaOH solution. How many mL of base must be added to get to the equivalence point? (The Ka of CH3COOH = 1.8 × 10-5)
- 80.0 mL of 0.100 M NH3 is titrated with 0.200 M HClO4. (The Kb of NH3 is 1.77 × 10-5) Calculate the pH at the following points:
- Initially, before any HClO4 has been added
- When 15.0 mL HClO4 has been added
- When 32.0 mL HClO4 has been added
- When 40.0 mL HClO4 has been added
- When 80.0 mL HClO4 has been added
Answers to Chemistry End of Section Exercises
-
- HNO2(aq) + OH-(aq) ⇌ NO2-(aq) + H2O(l)
- Na+; this is a neutral ion and will not affect the pH
- 0.0500 moles
- 1.00 × 102 mL
- 8.327
-
- NH3(aq) + H3O+(aq) ⇌ NH4+(aq) + H2O(l)
- Cl-; this is a neutral ion and will not affect the pH
- 0.100 moles
- 167 mL
- 4.837
- 40.0 mL
-
- 11.124
- 9.470
- 8.646
- 5.212
- 1.301


Feedback/Errata