Unit Two
Day 20: Rate of Radioactive Decay
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 18-3 through 18-9, and/or Chapter 9.13-9.15 in the Additional Reading Materials section.
D20.1 Half-Life of a Reaction
The half-life (t1/2) of a reaction is the time required for the concentration of a reactant to be reduced to half its initial value. In each succeeding half-life, the remaining concentration of the reactant is halved.
First-Order Reactions
An equation for the half-life of a first-order reaction can be derived from the integrated rate law:
If we set the time t equal to the half-life, t1/2, then [latex][A]_{t_{1/2}} = \frac{1}{2}[A]_0[/latex]. Therefore:
Thus:
The half-life of a first-order reaction is inversely proportional to the rate constant k, and, conveniently, is independent of the concentration of the reactant. A fast reaction (shorter half-life) has a larger k; a slow reaction (longer half-life) has a smaller k.
Example 1
Calculation of a First-order Rate Constant using Half-Life
Some dyes can be decomposed by sunlight. Use the data in the figure to determine whether the reaction is first order and to calculate the rate constant for decomposition of a green dye dissolved in water and left outdoors in sunlight at 40 °C.

Solution
It takes 6 hours for the 1.000-M solution to decrease to 0.500 M; it takes another 6 hours for the concentration to reach 0.250 M, and each successive halving also takes 6 h. Therefore the half-life for the decomposition is 6 h or 2.16 × 104 s. Because the half-life is independent of concentration, it is reasonable to assume the reaction is first order. (Subsequent sections in today’s work show that for other reaction orders, half-lives vary with concentration.) To find the rate constant at 40 °C:
Check Your Learning
The first-order radioactive decay of iodine-131 exhibits a rate constant of 0.138 d−1. What is the half-life for this decay?
Answer:
5.02 d.
Second-Order Reactions
The equation for half-life of a second-order reaction can be derived this way:
When t = t1/2 and [latex][A]_{t_{1/2}} = \frac{1}{2}[A]_0[/latex],
Thus,
For a second-order reaction, t1/2 is inversely proportional to the concentration of the reactant, and hence is not constant throughout the reaction. It increases as the reaction proceeds due to decreasing concentration of reactant. Consequently, unlike the situation with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.
Zeroth-Order Reactions
For a zeroth-order reaction,
When t = t1/2 and [latex][A]_{t_{1/2}} = \frac{1}{2}[A]_0[/latex]:
and
The half-life of a zeroth-order reaction decreases as the initial concentration decreases.
Equations for both differential and integrated rate laws and the corresponding half-lives for zero-, first-, and second-order reactions are summarized in Table 1.
| Property | Zeroth-Order | First-Order | Second-Order |
|---|---|---|---|
| rate law | rate = k | rate = k[A] | rate = k[A]2 |
| units of rate constant | M s−1 | s−1 | M−1 s−1 |
| integrated rate law | [A]t = −kt + [A]0 | ln[A]t = −kt + ln[A]0 | [latex]\dfrac{1}{[A]_t} = kt\;+\;(\dfrac{1}{[A]_0})[/latex] |
| plot needed for linear fit of rate data | [A] vs. t | ln[A] vs. t | [latex]\dfrac{1}{[A]}\;\text{vs.}\;t[/latex] |
| relationship between slope of linear plot and rate constant | k = −slope | k = −slope | k = +slope |
| half-life | [latex]t_{1/2} = \dfrac{[A]_0}{2k}[/latex] | [latex]t_{1/2} = \dfrac{0.693}{k}[/latex] | [latex]t_{1/2} = \dfrac{1}{[A]_0k}[/latex] |
| Table 1. Summary of Rate Laws for Zeroth-, First-, and Second-Order Reactions | |||
Exercise 1: Half-Life, Rate, and Concentration
D20.2 Radioactive Half-Lives
Most radioactive decay follows first-order kinetics, and hence radioactive decay has a characteristic, constant half-life. An isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, and how long a sample of an undesirable or dangerous isotope must be stored before it decays to a sufficiently low radiation level.
For example, cobalt-60, an isotope that emits gamma rays used to treat cancer, has a half-life of 5.27 years (Figure 1). In a given cobalt-60 source, since half of the [latex]_{27}^{60}\text{Co}[/latex] nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation produced is directly proportional to the rate of decay of the substance and the quantity of the substance.)
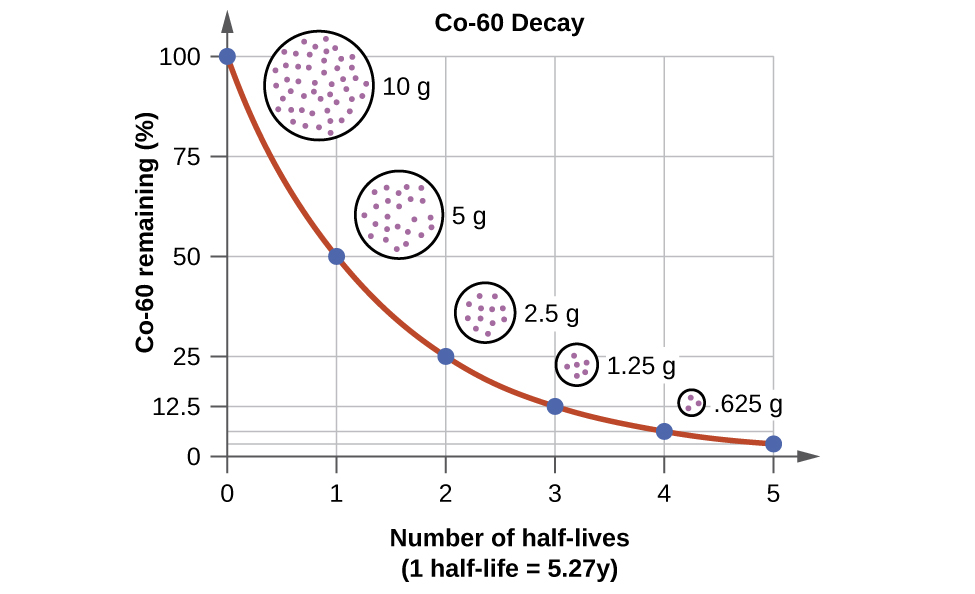
Radioactive decay occurs in atomic nuclei and therefore does not depend on chemical bonding or collisions of molecules. Each nuclide has a particular probability that a nucleus will decay in a given time. The more nuclei there are, the greater the number of nuclear decays during that time, so the rate of radioactive decay is proportional to the number of atomic nuclei present, N. The rate constant, k, for nuclear decay is called the decay constant. Hence, the rate of radioactive decay is:
The decay rate in nuclear decays per second is called the activity of the radioactive sample. The decay constant is related to the half-life by,
The first-order equations relating amount, N, and time are:
where N0 is the initial number of nuclei or moles of the isotope, and Nt is the number of nuclei/moles remaining at time t.
Example 2
Rates of Radioactive Decay
[latex]_{27}^{60}\text{Co}[/latex] decays with a half-life of 5.27 years to produce [latex]_{28}^{60}\text{Ni}[/latex].
(a) Calculate the decay constant for the radioactive disintegration of cobalt-60.
(b) Calculate the fraction of a sample of the [latex]_{27}^{60}\text{Co}[/latex] isotope that remains after 15.0 years.
(c) Calculate the time required for a sample of [latex]_{27}^{60}\text{Co}[/latex] to disintegrate to the extent that only 2.0% of the original number of nuclei remain.
Solution
(a) The value of the rate constant is given by:
(b) The fraction of [latex]_{27}^{60}\text{Co}[/latex] that is left after time t is given by [latex]\frac{N_t}{N_0}[/latex]. Rearranging the first-order relationship [latex]N_t = N_0e^{-kt}[/latex] to solve for this ratio yields:
The fraction of [latex]_{27}^{60}\text{Co}[/latex] that remains after 15.0 years is 0.138, or 13.8%.
(c) 2.00% of the original nuclei of [latex]_{27}^{60}\text{Co}[/latex] is equal to 0.0200×N0. Substituting this into the equation for time gives,
Check Your Learning
Radon-222, [latex]_{86}^{222}\text{Rn}[/latex], has a half-life of 3.823 days. Calculate the time required for a sample of radon-222 with a mass of 0.750 g to decay so that only 0.100 g of radon-222 is left.
Answer:
11.1 days
Exercise 2: Mass of Radioactive Nuclide Remaining
59Fe has a half-life of 44.5 days. For a 0.56-mg sample of 59Fe, calculate the mass, in mg, that remains after 1 year. Enter your numeric answer in the blank as a decimal fraction (not in scientific notation), include two significant figures.
D20.3 Radiometric Dating
Several radioisotopes have half-lives and other properties that make them useful for radiometric dating, the process of determining the date of origin of objects such as geological formations, archaeological artifacts, or formerly living organisms. Radiometric dating has been responsible for many breakthrough scientific discoveries about the geological history of the earth, the evolution of life, and the history of human civilizations. We will explore some of the most common types of radiometric dating and how the particular isotopes work for each type.
Radiometric Dating Using Carbon-14
Radiocarbon dating or carbon-14 dating can provide reasonably accurate dating of carbon-containing substances up to about 50,000 years old.
Naturally occurring carbon consists of three isotopes: [latex]_{\;\;6}^{12}\text{C}[/latex], which constitutes 99% of the carbon on earth; [latex]_{\;6}^{13}\text{C}[/latex], about 1% of the total; and trace amounts of [latex]_{\;\;6}^{14}\text{C}[/latex]. Carbon-14 is formed in the upper atmosphere by the reaction of nitrogen atoms with neutrons:
All isotopes of carbon react with oxygen to produce CO2. In the atmosphere, the ratio of 14CO2 to 12CO2 depends on the ratio of 14C to 12C, and the natural abundance of 14C is approximately 1 part per trillion. Analysis of carbon-containing gas samples trapped in Greenland ice sheets provides data on the 14C:12C ratio in the past, and the ratio has been nearly constant.
The incorporation of 14CO2 and 12CO2 into plants is a regular part of photosynthesis, which means that the 14C:12C ratio found in a living plant is the same as the 14C:12C ratio in the atmosphere. But when the plant dies, it no longer traps additional carbon through photosynthesis. Because 12C is a stable isotope and does not undergo radioactive decay, its concentration in the plant does not change. However, 14C decays by β emission with a half-life of 5730 years:
Thus, the 14C:12C ratio gradually decreases after the plant dies. The decrease in the ratio over time provides a measure of the time that has elapsed since the death of the plant. Throughout their lifetimes organisms that feed on plants also take up 14C with abundance the same as the atmosphere; when they die the 14C decays and the 14C:12C ratio gradually decreases. Figure 2 depicts this process.
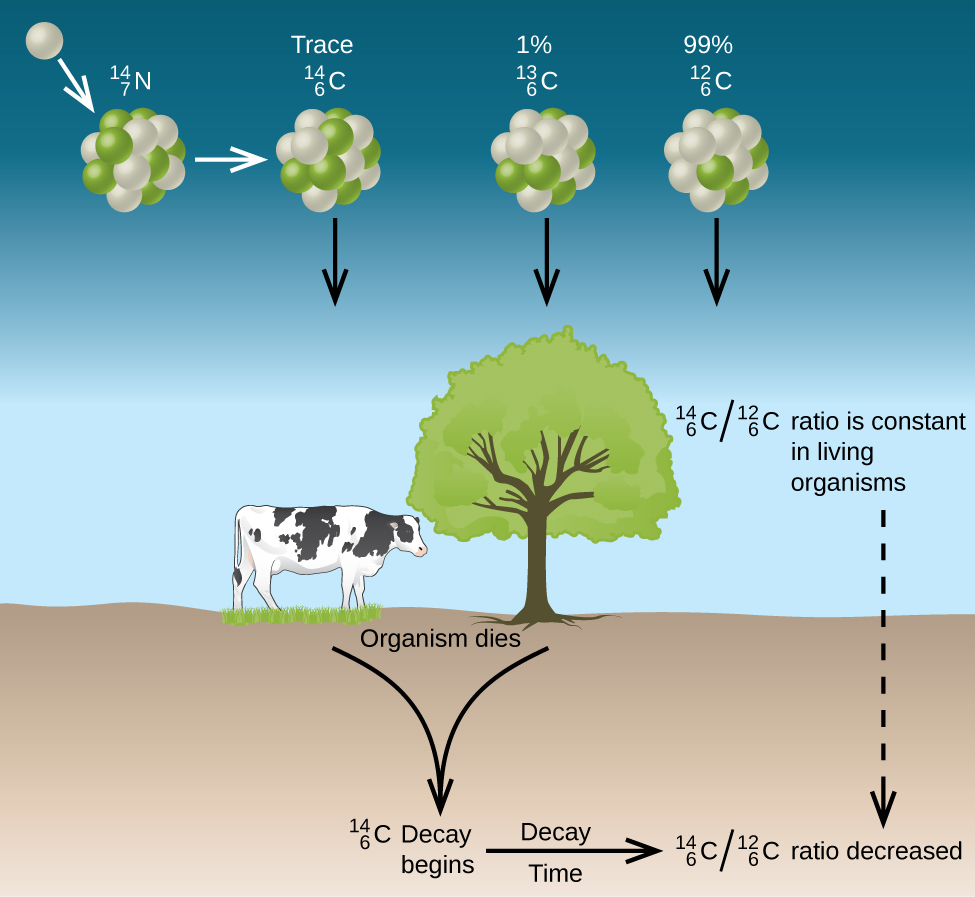
For example, if the 14C:12C ratio in a wooden object found in an archaeological dig is half what it is in a living tree, this indicates that 5730 years have elapsed since the death of the tree from which the wooden object was made. Highly accurate determinations of 14C:12C ratios can be obtained from very small samples (as little as a milligram) by the use of a mass spectrometer.
Example 3
Radiocarbon Dating
The first radiocarbon dating of the Dead Sea Scrolls was in 1950. A tiny piece of paper (produced from formerly living plant matter) taken from the Dead Sea Scrolls was found to have an activity of 10.8 disintegrations per minute per gram of carbon. If the initial 14C activity was 13.6 disintegrations/min/g of C, estimate the age of the Dead Sea Scrolls. (The half-life of 14C is 5730 years)
Solution
The activity, or rate of decay, is proportional to the amount of radioactive 14C left in the paper (decay rate = kN), so we can substitute the decay rates for the amount of 14C, N, in the relationship:
where the subscript 0 represents the time when the plants were cut to make the paper, and the subscript t represents the current time.
The decay constant can be determined from the half-life of 14C:
Substituting and solving, we have:
Therefore, the Dead Sea Scrolls are approximately 1900 years old.

Check Your Learning
More accurate dates of the reigns of ancient Egyptian pharaohs have been determined recently using plants that were preserved in their tombs. Samples of seeds and plant matter from King Tutankhamun’s tomb have a 14C decay rate of 9.07 disintegrations/min/g of C. How long ago did King Tut’s reign come to an end?
Answer:
about 3350 years ago, or approximately 1340 BC
The accuracy of this technique depends on the 14C:12C ratio in a living plant being the same now as it was in an earlier era, but this is not always valid. For example, right now, due to the increasing accumulation of CO2 (largely 12CO2) in the atmosphere, caused by combustion of fossil fuels in which essentially all of the 14C has decayed, the 14C:12C ratio in our atmosphere is decreasing. This in turn affects the 14C:12C ratio in currently living organisms on the earth. Fortunately, we can use other data, such as tree dating via examination of annual growth rings, to calculate correction factors. With these correction factors, more accurate dates can be determined. In general, radioactive dating only works for about 10 half-lives; therefore, the limit for carbon-14 dating is about 57,000 years.
Radiometric Dating Using Nuclides Other than Carbon-14
Radiometric dating can also use other radioactive nuclides with longer half-lives to date older events.
For example, uranium-238 can be used for establishing the age of rocks (and the approximate age of the oldest rocks on earth). Since 238U has a half-life of 4.5 billion years, it takes that amount of time for half of the original 238U to decay into 206Pb. In a sample of rock that does not contain appreciable amounts of 208Pb, the most abundant isotope of lead, we can assume that lead was not present when the rock was formed. Therefore, by measuring and analyzing the ratio of 238U:206Pb, we can determine the age of the rock. This assumes that all of the 206Pb present came from the decay of 238U. If there is 206Pb from other sources than 238U present, which is indicated by the presence of lead isotopes with mass number other than 206 in the sample, it is necessary to make adjustments in the calculations.
Potassium-argon dating uses a similar method. 40K decays by positron emission and electron capture to form 40Ar with a half-life of 1.25 billion years. If a rock sample is crushed and the amount of 40Ar gas that escapes is measured, determination of the 40Ar:40K ratio yields the age of the rock. Other methods, such as rubidium-strontium dating (87Rb decays into 87Sr with a half-life of 48.8 billion years), operate on the same principle. To estimate the lower limit for the earth’s age, scientists determine the age of various rocks and minerals, making the assumption that the earth is older than the oldest rocks and minerals in its crust. As of 2014, the oldest known rocks on earth are the Jack Hills zircons from Australia, found by uranium-lead dating to be almost 4.4 billion years old.
Podia Question
A sample of an igneous rock contains 9.58 × 10–5 g of 238U, 2.51 × 10–5 g of 206Pb, and a negligible quantity of 208Pb. No other lead isotopes are detected. Determine the approximate time at which the rock was formed. (238U decays into 206Pb with a half-life of 4.5 × 109 y.)
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

