D25.2 Effect of Temperature on Equilibrium

Jia Zhou; John Moore

D25.2 Effect of Temperature on Equilibrium

Recall that:

Δ_rG° = Δ_rH° – TΔ_rS° and Δ_rG° = −RT(lnK°)

Therefore:

−RT(lnK°) = Δ_rH° – TΔ_rS°

This equation can be used to calculate K° at different temperatures, if we assume that Δ_rH° and Δ_rS° for a reaction have the same values at all temperatures. This is a good, but not perfect, assumption. It is not a good assumption if there is a phase change for a reactant or a product within the temperature range of interest.

Dividing both sides of the equation by -RT gives:

lnK°	=	$-\dfrac{{\Delta}_rH^{\circ}}{R}\left(\dfrac{1}{T}\right)$	+	$\dfrac{{\Delta}_rS^{\circ}}{R}$
y	=	mx	+	b

A plot of lnK° vs. $\frac{1}{T}$ is called a van’t Hoff plot. The graph has a slope of $-\frac{{\Delta}_rH^{\circ}}{R}$ . Therefore, if the concentrations of reactants and products are measured at various temperatures so that K° can be calculated at each temperature, the reaction’s Δ_rH° can be obtained from a van’t Hoff plot.

**Figure: Van’t Hoff plots**. The reaction N₂ + O₂ ⇄ 2 NO has Δ_rH° = 180.5 kJ/mol. For this endothermic reaction, as T increases (1/T decreases) the equilibrium constant increases. The reaction N₂ + 3 H₂ ⇄ 2 NH₃ has Δ_rH° = −92.2 kJ/mol. For this exothermic reaction, as T increases (1/T decreases) the equilibrium constant decreases.

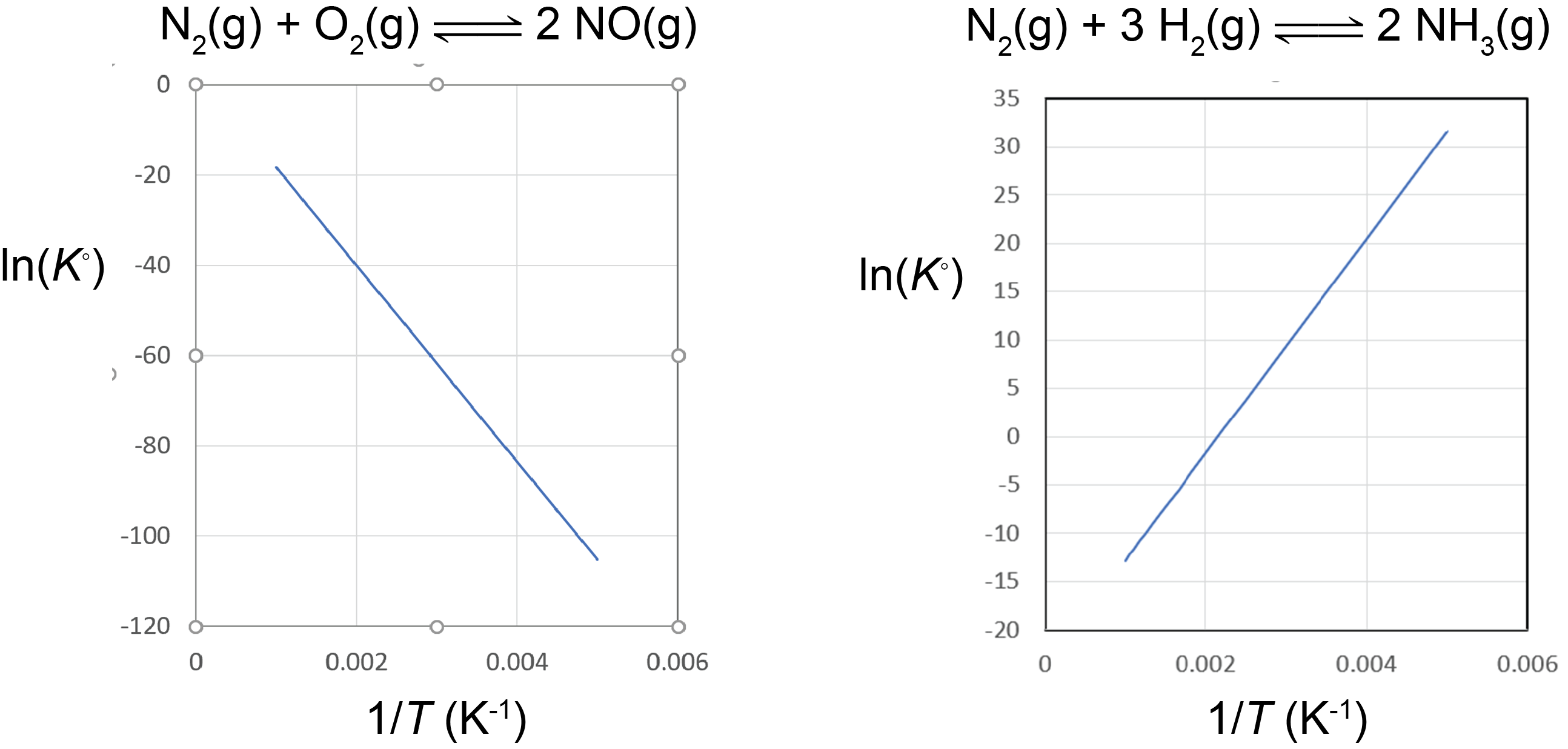
Based on the equation for the van’t Hoff plot, an exothermic reaction (Δ_rH° < 0) has K° decreasing with increasing temperature, and an endothermic reaction (Δ_rH° > 0) has K° increasing with increasing temperature. The magnitude of Δ_rH° will dictate how rapidly K° changes as a function of temperature.

For example, suppose that K°₁ and K°₂ are the equilibrium constants for a reaction at temperatures T₁ and T₂, respectively:

$\text{ln}K_1^{\circ} = -\dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_1}\right)\;+\;\dfrac{{\Delta}_{\text{r}}S^{\circ}}{R}$

$\text{ln}K_2^{\circ} = -\dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_2}\right)\;+\;\dfrac{{\Delta}_{\text{r}}S^{\circ}}{R}$

Subtracting the two equations yields:

$\begin{array}{rcl}\text{ln}K_2^{\circ}\;-\;\text{ln}K_1^{\circ} &=& \left(-\dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_2}\right)\;+\;\dfrac{{\Delta}_{\text{r}}S^{\circ}}{R}\right) - \left(-\dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_1}\right)\;+\;\dfrac{{\Delta}_{\text{r}}S^{\circ}}{R}\right)\\[1em] \text{ln}\left(\dfrac{K_2^{\circ}}{K_1^{\circ}}\right) &=& -\dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_2}\;-\;\dfrac{1}{T_1}\right)\\[1em] \text{ln}\left(\dfrac{K_2^{\circ}}{K_1^{\circ}}\right) &=& \dfrac{{\Delta}_{\text{r}}H^{\circ}}{R}\left(\dfrac{1}{T_1}\;-\;\dfrac{1}{T_2}\right) \end{array}$

Thus calculating Δ_rH° from tabulated Δ_fH° values and measuring the equilibrium constant at one temperature would allow us to calculate the equilibrium constant at any other temperature (assuming that Δ_rH° and Δ_rS° are independent of temperature).

Using this equation, you can also estimate Δ_rH° without constructing a van’t Hoff plot if K° was determined at only two temperatures (but the result will not be as accurate as a van’t Hoff plot constructed from numerous data points).

Exercise: Temperature Dependence of the Equilibrium Constant

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License