D6.4 MOs for Second-row Diatomic Molecules
Let’s consider some slightly more complex examples of molecular orbitals. F2, O2, and N2 are diatomic molecules formed by elements from the second row of the periodic table. These molecules contain many more electrons than H2, and their molecular orbitals are derived from p atomic orbitals as well as s atomic orbitals.
Activity: Shapes and Phases of p Atomic Orbitals
Draw a Cartesian coordinate system showing x, y, and z axes and draw a schematic diagram of a 2px atomic orbital. Show phases using two different colors, shading/no shading, or plus/minus signs. On a second coordinate system, make a similar drawing of a 2pz atomic orbital.
Draw in your notebook, then left-click here for an explanation.
The 2px orbital has one phase along the positive x axis and the opposite phase along the negative x axis. The 2pz orbital is similar, but oriented along the z axis. The orbital diagrams look like this:
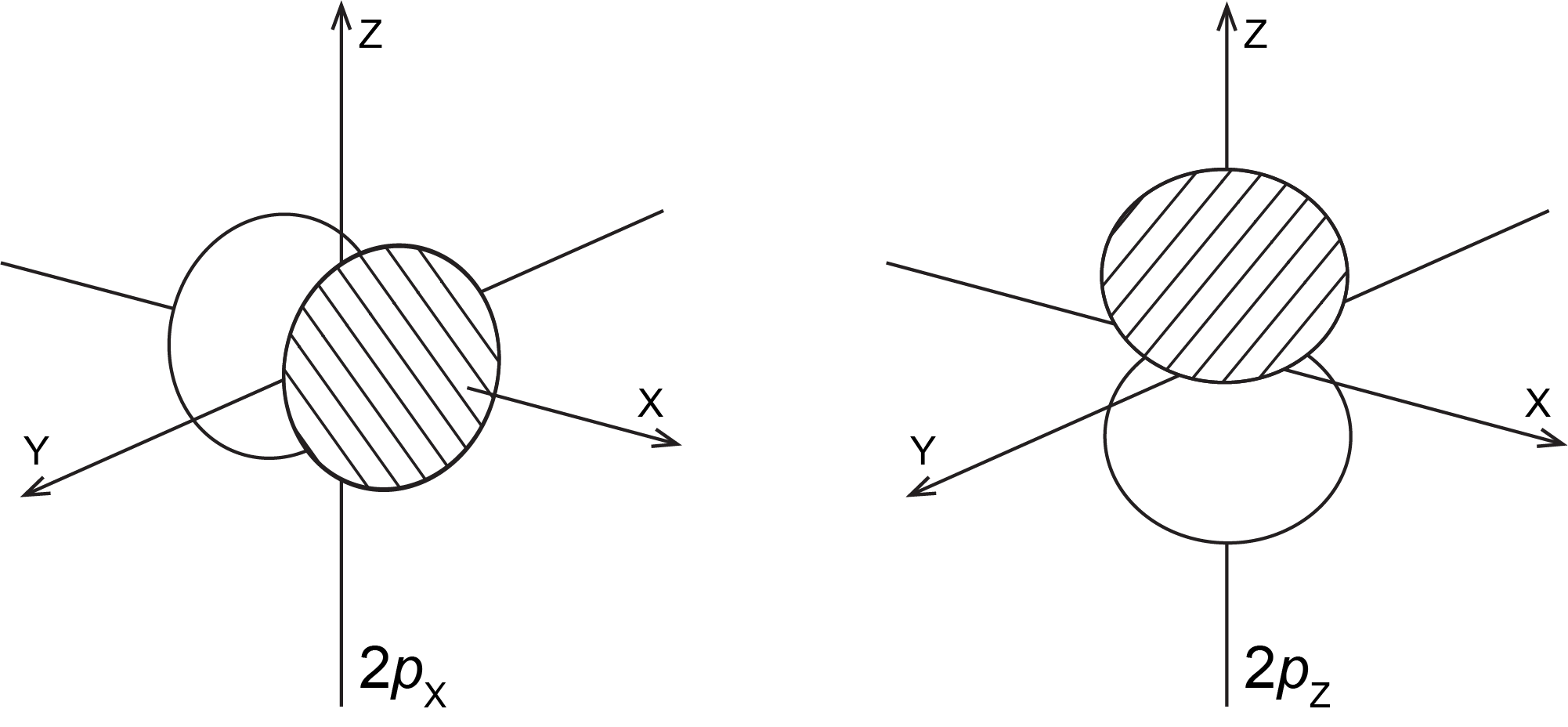
Suppose you spin an atom around the z-axis. Classify the 2px, 2py, and 2pz orbitals with respect to cylindrical symmetry around the z-axis. Which orbital does not have a node that contains the z-axis?
Write in your notebook, then left-click here for an explanation.
The 2pz orbital is cylindrically symmetric around the z-axis: it looks the same no matter what the angle of rotation is. The nodal plane of the 2pz orbital is the x-y plane, which does not contain the z-axis.
The 2px orbital is not cylindrically symmetric around the z-axis. If you rotate the px orbital 180° around the z-axis, the + and − phases are exchanged; also, the orbital looks different for every angle of rotation.
The nodal plane of the 2px orbital contains the origin of the coordinate system and is perpendicular to the x-axis; the z-axis lies in this nodal plane. This is another way to tell that the 2px orbital is not cylindrically symmetric around the z-axis.
The 2py orbital also is not cylindrically symmetric around the z-axis and has a node that contains the z-axis.
Now think about what happens when two atoms containing 2p atomic orbitals approach each other. Assume that the internuclear axis is the z axis. This means that the 2pz atomic orbitals are aligned along the internuclear axis while the 2px and 2py atomic orbitals are oriented perpendicular to the internuclear axis.
When the two atoms approach, the bonding and antibonding overlap of the two 2pz atomic orbitals occurs along the internuclear axis (z axis):

MOs derived from these two combinations are labeled σ2pz and σ*2pz. If you don’t understand why these MOs are have the label σ, review the section on MO diagrams.
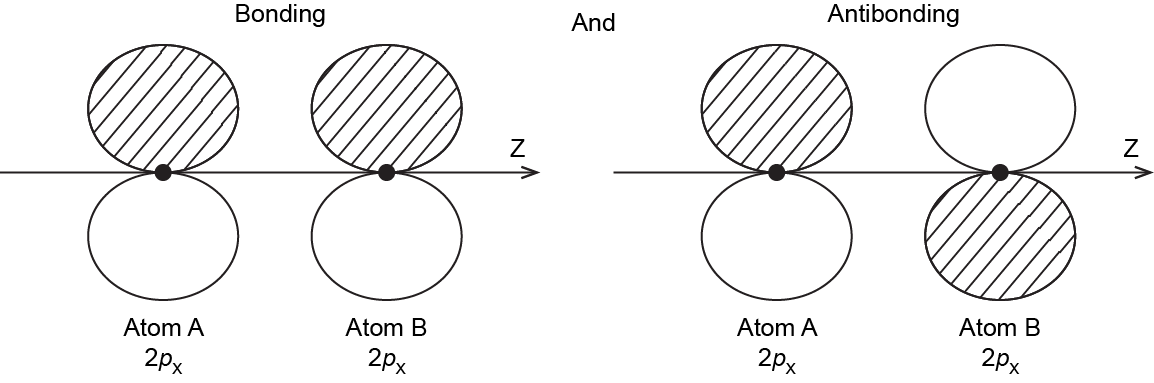
It is also possible to make bonding and antibonding combinations from the two 2px AOs and from the two 2py AOs. Here is a diagram for the two ways the 2px AOs can overlap. Notice that the orbitals overlap side-by-side, not end-on, because the 2px AOs are aligned perpendicular to the internuclear axis (z axis).
Activity: Molecular Orbitals Involving p Atomic Orbitals
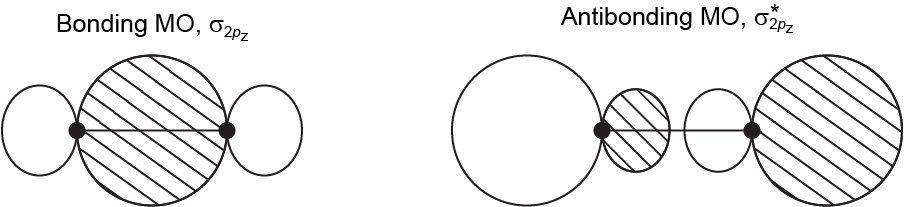
Assume that two atoms approach along the z axis. Draw two diagrams showing MOs formed from two 2pz AOs, one on each of the atoms. Label one diagram “Bonding MO, σ2pz” and the other diagram “Antibonding MO, σ∗2pz“. Explain why you labeled each MO as you did. (Note that these diagrams are derived from, but not the same as, the diagrams above.)
Draw and label in your notebook, then left-click here for an explanation.
When the orbitals overlap so that the phases match between the nuclei, there is bonding. When the orbitals are out of phase there is antibonding. The orbitals are labeled σ because they are cylindrically symmetric around the internuclear axis (there is no node that contains the internuclear axis).
The orbital diagrams look like this:
Consider overlap of a 2px AO on each of two atoms, which approach along the z axis. (Assume that the x axis on one atom is parallel to the x axis on the other atom.) Draw a MO that is a bonding combination of the two 2px AOs and a MO that is antibonding. Label each orbital as bonding or antibonding and as sigma or pi. Explain why you labeled each orbital as you did.
Draw and label in your notebook, then left-click here for an explanation.
When the atomic orbitals overlap so that the phases match between the nuclei, there is bonding and a bonding MO forms. When the AOs are out of phase there is antibonding. The AOs were oriented side-by-side (perpendicular to the internuclear axis); therefore, the AOs were not cylindrically symmetric and the MO is also not cylindrically symmetric. Because each MO has one node that contains the internuclear axis, the orbitals are labeled π. (A MO with two nodes containing the internuclear axis is labeled δ.)
The orbital diagrams look like this:
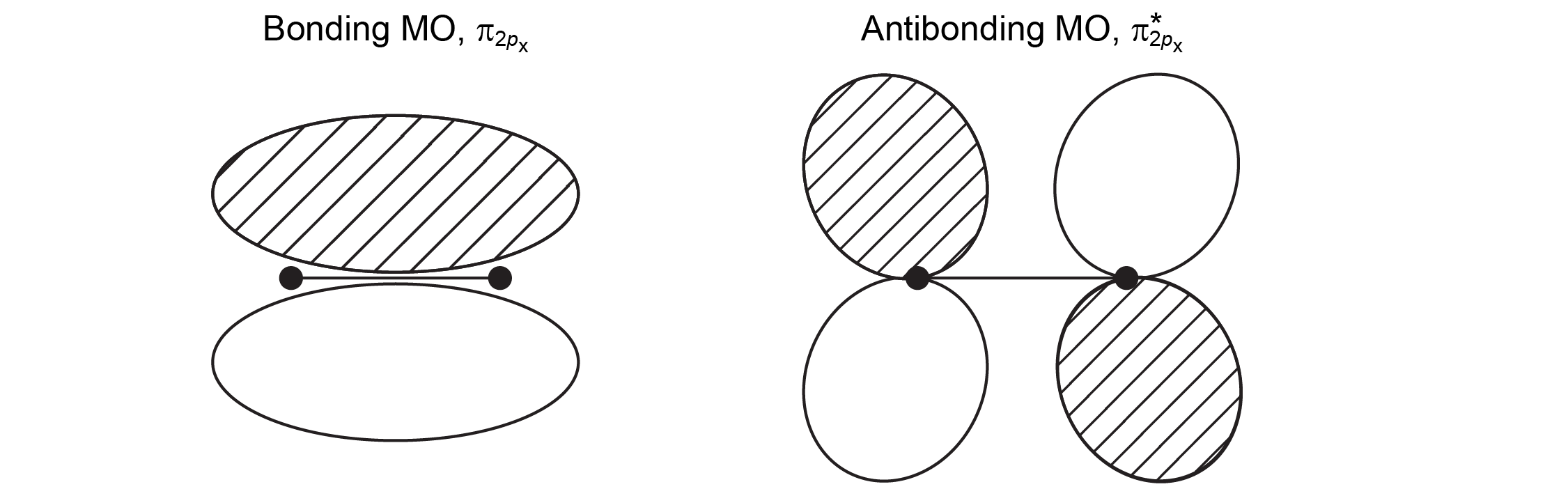
When two 2p AOs overlap side-by-side, the bonding MO formed is not symmetric with respect to rotation around the internuclear axis. Thus, the bond formed is not a σ bond. If you look down the internuclear (bond) axis, the “side view” of the MO looks similar to a 2p atomic orbital; this MO is called a π orbital.
Think about all atomic orbitals that are occupied in a fluorine atom, F: 1s, 2s, 2pz, 2px, and 2py. For each pair of AOs (such as 2s on atom A with 2s on atom B), overlap produces one bonding and one antibonding MO. There is σ and σ* for 1s – 1s, 2s – 2s, and 2pz – 2pz overlaps. There is π and π* for 2px – 2px, and 2py – 2py overlaps. These ideas result in the MO energy-level diagram shown here:

From the ten AOs (five from each F atom), ten MOs are formed in F2. Note that whether a MO is bonding or antibonding is dependent on whether it is lower or higher in energy than the AOs from which it is derived. Hence, even though σ*2s is lower in energy than σ2pz, it is still an antibonding MO.
The y-axis in the above figure only shows qualitative relative energy ordering. If you consider the actual energy values, the core electrons are much much lower in energy than the valence electrons. For example, the energy difference between the 1s and 2s atomic orbitals in F is 62,000 kJ/mol while the difference between 2s and 2p is only 1,800 kJ/mol. The core electrons also occupy orbitals that are much smaller (closer to their nucleus) than valence electrons. Hence, the core electrons from two atoms will not overlap in any significant way even as their valence electrons overlap to form covalent bonds. This is why you will often see the core electrons omitted from MO diagrams. (Such omission will not hinder your analysis of the molecule. For example, results from bond order calculations will be the same with or without core electrons.)
We also see in Figure: MO Energies for F2 that the two π bonding MOs, π2px and π2py, are degenerate (have the same energy). This is because the side-by-side overlap of two 2px AOs is identical to the side-by-side overlap of two 2py AOs. They differ only in that π2px and π2py are perpendicular to each other, because the 2px AO is perpendicular to the 2py AO. Similar reasoning leads to the conclusion that the π*2px and π*2py MOs are also degenerate. Recognizing degenerate MOs is important when applying Hund’s rule to determine molecular electron configurations.
Figure: Pi-Bond MOs (below) shows the formation of the two perpendicular π bonds as two N atoms approach each other. (The two molecular depictions in the figure represent the same N2 molecule: one shows the 2px – 2px orbital overlap and the other shows the 2py – 2py orbital overlap.)
Exercise: Molecular Orbital Electron Configurations
Additional Practice
Based on the electron configuration for the F2 molecule, the π and π* MOs are all filled; there is no net π bond in the molecule. This is reflected in the bond order calculation: F2 has a bond order of 1, corresponding to a single σ bond.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

