D4.3 Periodic Variation in Ionization Energies
In addition to atomic radius, several other properties vary depending on position in the periodic table. Like atomic radius, these properties depend on effective nuclear charge and size of atomic shell.
The quantum mechanics model for the hydrogen atom discussed ionization of the hydrogen atom: excitation of the electron from the n = 1 level to the limit of n → ∞:
Ionization energy (IE), the minimum energy required to remove an electron from the atomic orbital it occupies (exciting it to n = ∞), also applies to multi-electron atoms. As shown in this table of ionization energies, there are successive ionization energies, one for each electron.
The first ionization energy (IE1) is the minimum energy required to remove the least tightly bound electron, i.e. the electron in the highest energy orbital. It corresponds to the process:
The second ionization energy (IE2) is the minimum energy required for removing an electron from the 1+ cation, corresponding to:
And so forth.
Electrons in atoms have lower potential energy than when they are separated from the atom, so energy is always required to remove an electron from atoms or ions. Ionization is an endothermic process and IE values are always positive.
Ionization energies can be determined experimentally from atomic spectra or by shining light on a gas-phase sample and successively increasing the photon energy until ejection of an electron is observed. Such experiments also give us direct information about the atomic orbital the electron was occupying.
Based on Coulomb’s law, it is reasonable that the least tightly held electron is easiest to remove because it is located farthest from the nucleus. Use what you have just learned about atomic radii to predict how first ionization energy varies
- from one atom to the next going across a row in the periodic table
- from one atom to the next going down a periodic group
Write each prediction in your notebook, then left-click here for an explanation.
According to Coulomb’s law, the force between nucleus and electron decreases as distance increases. Smaller attractive force allows an electron to be removed more easily. Because the least tightly bound electron is farthest from the nucleus and determines the size of an atom, as atomic radius increases, first ionization energy should decrease.
This predicts that, as a general rule, first ionization energy increases across a period and decreases down a group.
Exercise: Periodic Variation of Ionization Energy
In the preceding activity, you developed a general rule that across a period, IE1 increases with increasing atomic number, Z; down a group, IE1 decreases with increasing Z. Look at the Figure: Ionization Energies below and make certain you see how the data in the figure support both trends. There are a few systematic deviations from these trends, which also can be seen in the Figure.
Examine data presented in the figure. Identify all deviations from the trend that ionization energy increases across a period and decreases down a group. Click on each deviation involving an element in Period 1, Period 2, or Period 3.
In your notebook, write an explanation for the fact that IE1 for B is smaller than IE1 for Be. (It may help to write the electron configuration for each atom.)
Write in your notebook, then left-click here for an explanation.
B has one more proton than Be and the effective nuclear charge is greater because the n = 2 electrons do not screen the nuclear chage completely. Therefore, to a first approximation it should be harder to remove an electron from B and IE₁ for B should be larger.
Comparing electron configurations, Be 1s22s2 versus B 1s22s22p1, we see that the electron lost from Be is in an s orbital but the electron lost from B is in a p orbital. Because the energy of a subshell increases as ℓ increases, within any shell the p electrons are higher in energy than the s electrons; thus, an s electron is harder to remove from an atom than a p electron in the same shell. This results in a lower first ionization energy for boron than for beryllium. There is a small deviation from the predicted trend each time a new subshell begins to be filled with electrons.
Another deviation occurs when a subshell becomes more than half filled. For example, oxygen’s IE1 is slightly lower than that for nitrogen. The orbital diagram of oxygen shows that the last electron added (red) is forced to pair with another electron, because the 2p subshell is more than half full.
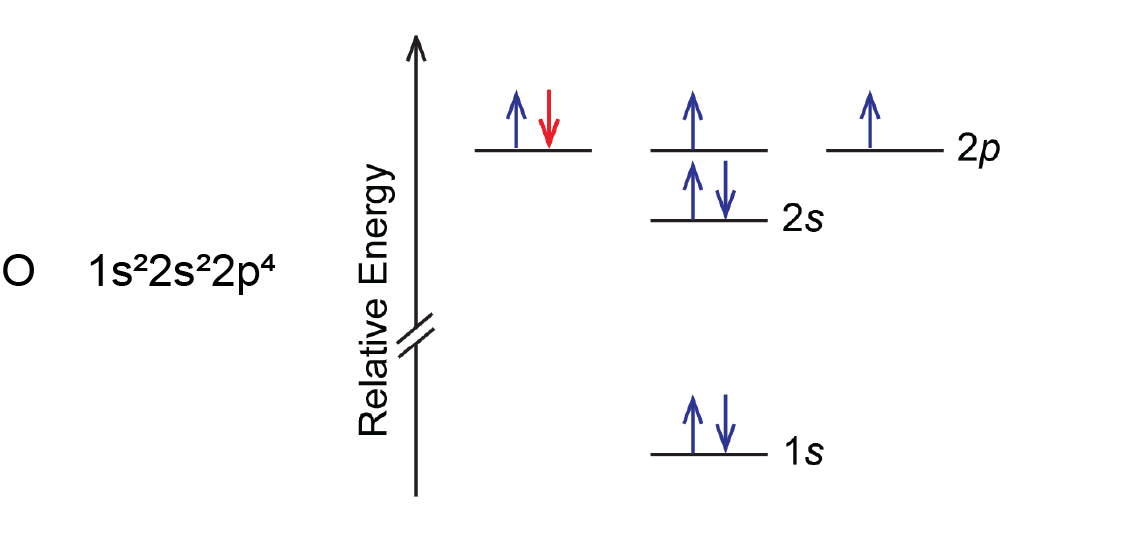
Loss of the electron (colored red in the orbital diagram) yields a greater reduction of electron–electron repulsion because there are no longer two electrons in the same orbital. This makes it easier to lose one electron from O and the ionization energy is smaller than expected. The same explanation applies to the dip for sulfur after phosphorus in Figure: Ionization Energies.
Looking at the successive IEs in the appendix, we see that for any element, IE1 < IE2 < IE3, and so forth, and this is due to the greater Zeff in successively more positive ions. However, sometimes the increase in successive IE is larger than expected. For example, consider the data in Table 1:
| Element | IE1 | IE2 | IE3 | IE4 | IE5 | IE6 | IE7 |
|---|---|---|---|---|---|---|---|
| K | 419 | 3069 | 4438 | 5876 | 7975 | 9620 | 11385 |
| Ca | 590 | 1145 | 4941 | 6465 | 8142 | 10496 | 12350 |
| Sc | 633 | 1244 | 2388 | 7130 | 8877 | 10720 | 13314 |
| Ga | 579 | 1982 | 2962 | 6194 | 8299 | 10874 | 13585 |
| Ge | 760 | 1537 | 3301 | 4409 | 9012 | 11183 | 13981 |
| As | 947 | 1949 | 2731 | 4834 | 6040 | 12302 | 14183 |
| Table. Successive Ionization Energies (IEs) for Some Period-4 Elements (kJ/mol) | |||||||
Determine the number of valence electrons for each atom:
K Sc Ga
Correlate the electron configuration and number of valence electrons with the IE data in the Table above. Write a clear, concise explanation of why the larger IE increases occur where they do.
Write in your notebook, then left-click here for an explanation.
K ([Ar]4s1) has a single valence electron. The second ionization energy is much larger than the first. The first ionization energy corresponds to loss of the single valence electron. The second ionization energy has to correspond to loss of a core electron, because there are no valence electrons left. Core electrons are more tightly held by nuclear charge and much harder to remove.
Sc ([Ar]4s23d1) has three valence electrons. Each of the first three ionization energies is a bit less than double the one before it, reflecting the effect of increasing charges of the cations. The fourth ionization energy is almost three times larger than the third, corresponding to loss of one of the core electrons. It is much harder to make a Sc4+ ion than a Sc3+ ion.
Ga ([Ar]4s23d104p1) has only three valence electrons. (Electrons in the completely filled 3d subshell are core electrons). There are two big jumps in ionization energy: IE2 is more than three times IE1 and IE4 is more than double IE3, whereas IE3 is only 1.5 times IE2. These jumps can be explained by the electron configuration. The 4p subshell is higher in energy than the 4s subshell so loss of the single 4p electron is relatively easy but loss of a second electron, a 4s electron is harder. Losing the third (and last) valence electron, also a 4s electron, requires only a little more energy than losing the second electron. However, a good deal more energy is required to remove a core electron from the 3d subshell.
These observed ionization energies are consistent with the idea of valence electrons—electrons in outer shell(s) that are less bound and more energetically accessible, allowing them to participate in chemical transformations.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

