D22.2 Predicting the Sign of ΔS

The relationships between entropy, microstates, and matter/energy dispersal make it possible for us to assess relative entropies of substances and predict the sign of entropy changes for chemical and physical processes.

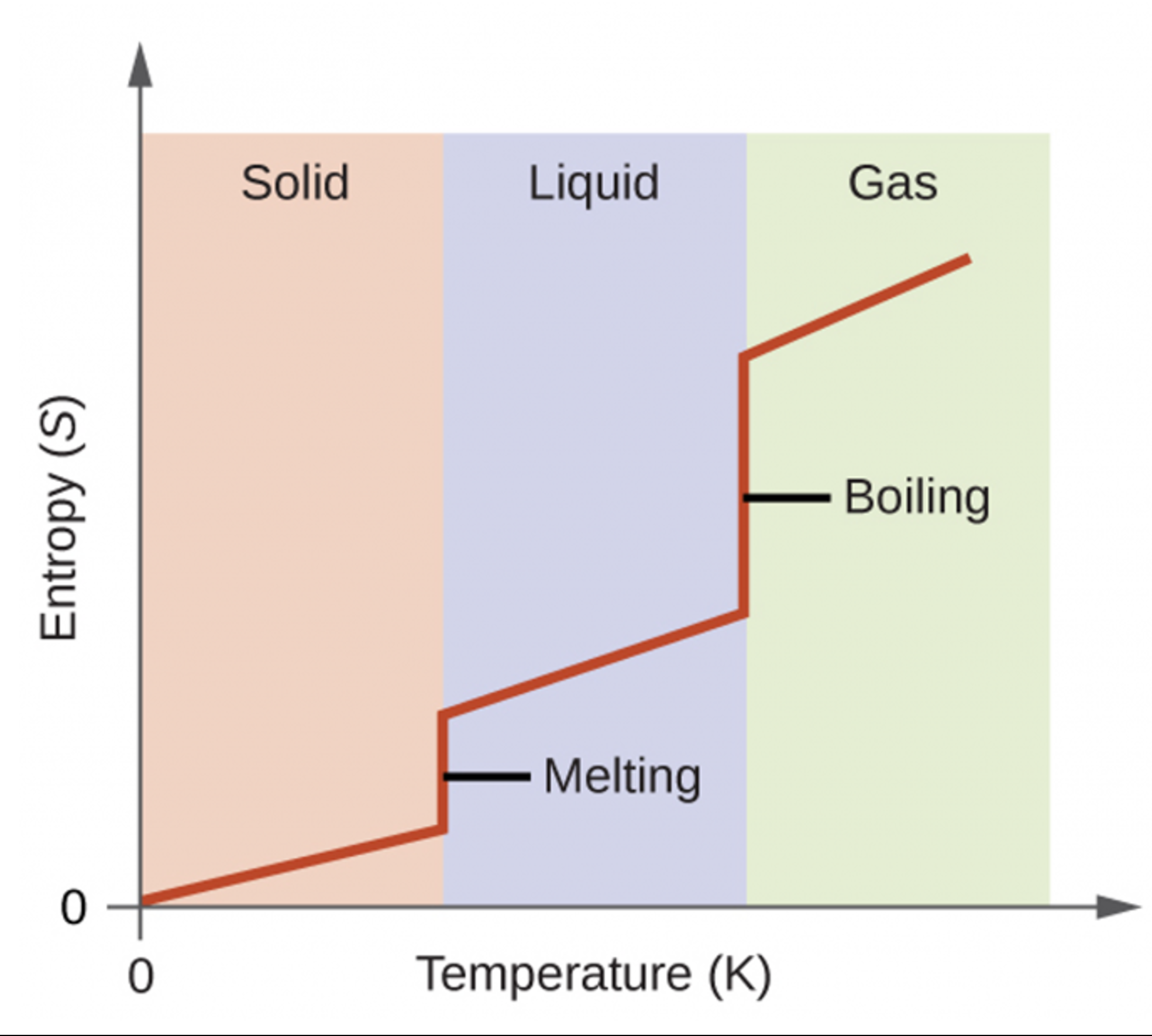
Consider the atomic-scale models of solid, liquid, and gas illustrated in the figure below. In the solid phase, the molecules (represented as spheres) are restricted to nearly fixed positions relative to each other and only oscillate a little about these positions; the number of microstates (W_solid) is relatively small. In the liquid phase, the molecules can move over and around each other, though they remain in relatively close proximity. This increased freedom of motion results in a greater variation in possible particle energy allocation, W_liquid > W_solid. As a result, S_liquid > S_solid and the process of melting is characterized by an increase in entropy, ΔS > 0.

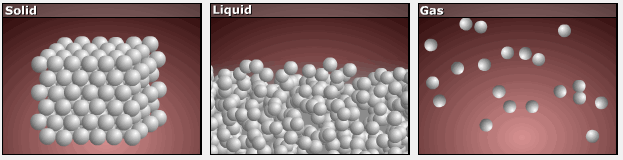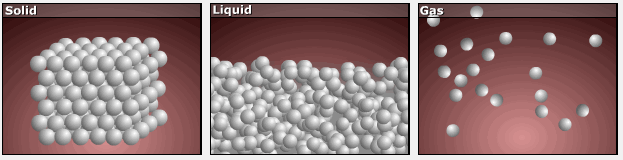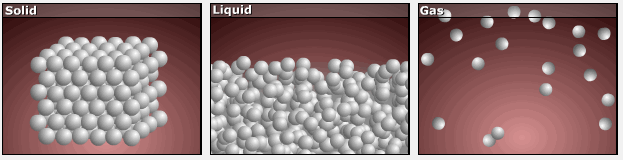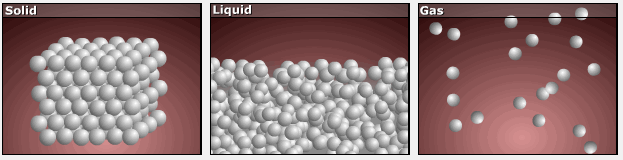
Solids and liquids have surfaces that define their volume, but in the gas phase the molecules occupy the entire container. Therefore, for the same sample, each molecule in a gas has much higher freedom of motion (and there are many more microstates) than in the liquid or solid phase. Consequently, S_gas > S_liquid > S_solid, and the processes of vaporization and sublimation involve increases in entropy, ΔS > 0.

The temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature results in more extensive vibrations of the particles in solids and more rapid movements of the particles in liquids and gases. Thus, the entropy for any substance increases with temperature.

The entropy of a substance is also influenced by the structure of the particles that the substance comprises. For atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms. For heavier atoms the energy levels corresponding to movement from one place to another are closer together, which means that at a given temperature there are more occupied energy levels and more microstates. For molecules, greater number of atoms (regardless of their masses) within a molecule gives rise to more ways in which the molecule can vibrate, which increases the number of possible microstates. Thus, the more atoms there are in a molecule the greater the entropy is.

Finally, variations in the types of particles affects the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of different particle types is greater due to the additional orientations and interactions that are possible. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates.