D12.2 Hybridization in Resonance Structures
The assignment of hybridization and molecular geometry for molecules that have two or more major resonance structures is the same as the process for a single Lewis structure. There is one caveat: the hybridization (and hence molecular geometry) assigned to one resonance structure must be the same as all other resonance structures in the set. This is because a set of resonance structures describes a single molecule.
Therefore, when assigning hybridization, consider all the major resonance structures. If an atom’s nhyb is different in one resonance structure from another, then use the smaller nhyb to determine hybridization of that atom.
Exercise: Molecular Structure of Resonance Hybrid
In formamide, the delocalized π molecular orbital extends over the oxygen, carbon, and nitrogen atoms (see figure below). This is also described by the set of resonance structures, where there is a partial double-bond character between O and C as well as between C and N. An unhybridized 2p atomic orbital on the N atom must contribute to this π bond. Therefore, the N atom must have sp2 hybridization (it forms three σ bonds) and a trigonal planar local geometry. If N had an sp3 hybridization, it would not be able to participate in the π bond.
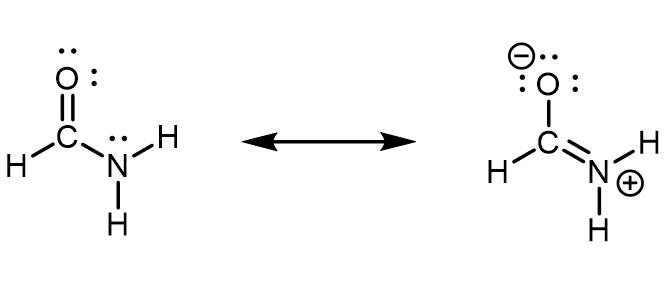
When looking at the left resonance structure, you might be tempted to assign sp3 hybridization to N given its similarity to ammonia (NH3). However, this is a resonance structure; the set of resonance structures describes a molecule that cannot be described correctly by a single Lewis structure. All atoms must remain in the same positions from one resonance structure to another in a set of resonance structures. There cannot be a N atom that is trigonal pyramidal in one resonance structure and trigonal planar in another resonance structure, because the atoms attached to the N would have to change positions.
Experimental evidence and quantum mechanics calculations show that formamide is a planar molecule, hence, the hybridization and geometry assignments are valid. This also means that the planar geometry must be more stable than the geometry involving a trigonal pyramidal sp3 N. In other words, participation in the π bonding stabilizes the sp2 hybridization of N.
Resonance Structures and Orbital Overlap (Valence Bond Theory)
In some molecules, electrons are “localized” in a specific region—a covalent bond or an electron lone pair on one atom. In others (like those we have been discussing in this and previous section), some of the electrons are “delocalized”—they are associated with more than one bonding or lone pair region, because the molecule’s structure allows for overlapping of adjacent unhybridized 2p orbitals.
For example, consider ozone (O3), for which you need to draw two resonance structures to describe the atom connectivity and distribution of valence electrons in the molecule.
In this representation, there are two electron pairs that are not localized to a particular bond or atom. These electron pairs seem to “move” between the two resonance structures. Move the slider to the center position in the above figure to follow the red electrons! The blue arrows represent how redistributing valence electrons results in these two resonance structures for ozone.
BUT, as discussed previously, the electrons DO NOT redistribute like this. They don’t redistribute at all—the individual resonance structures for O3 do not exist. The actual structure of O3 is an “average” of these two resonance structures. The above electron movement diagram is just an illustration of one way to think about electron delocalization within the limitations of Lewis structures.
But WHAT is it about the structure of a molecule that allows for this electron delocalization to occur? To answer this question, we can use valence bond theory to consider: what orbitals (if any) are available to overlap and form an uninterrupted pathway across the regions where electron delocalization is occurring?
Consider a valence bond model of O3. The central oxygen atom would utilize sp2 hybrid orbitals (giving rise to the “bent” geometry of the O3 molecule), while the oxygen atoms on the end would utilize sp hybrid orbitals (no matter which of the two resonance structures you interrogate). Move the slider to the rightmost position in the figure above to see.
Given these hybridizations, there would be at least one unhybridized 2p orbital on each oxygen atom whose electron density lobes are above and below the plane of the molecule. (Recall that the unhybridized 2p orbitals must be perpendicular to the hybrid orbitals involved in the σ bonding interactions.)
The overlap of these (parallel-to-each-other) unhybridized 2p orbitals gives rise to the “pathway” via which electron delocalization occurs in O3. This is what we have to imagine when we look at the resonance structures of O3.
You may recognize the overlap of adjacent parallel 2p orbitals as forming a π bond interaction. Indeed, both O–O bonds in O3 have “π-bonding character”. Because the two electron pairs are being delocalized across the molecule, some electron density is added to the O–O bonding regions (in addition to the Osp-Osp2 σ bonds). This results in O–O bonds that are stronger than typical “O–O” bonds but weaker than the “O=O” bond in O2. Indeed, this is reflected in the bond length data, which show that the O–O bonds in O3 are in between formal “O–O” and “O=O”. Moreover, it is experimentally more similar to “O=O” bonds than “O–O” bonds.
| Bond | Average length | Range |
| O-O | 168 ± 61 pm | 112-298 pm |
| O=O | 120 ± 5 pm | 120-121 pm |
| O-O in O3 | bond length = 128 pm | |
In the case of O3, electron delocalization occurs across the entire molecule, but some molecules may have electron delocalization occurring across only a portion of the molecule’s structure. For each molecule, you have to consider: what orbitals (if any) are available to overlap and allow for electron delocalization?
Left-click here for optional information: Why is electron delocalization a stabilizing phenomenon?
We can think about the energy associated with electron delocalization in terms of the potential and kinetic components.
For potential energy, according to Coulomb’s law, systems with stronger electron-electron repulsions will have a higher potential energy. Thus, the more localized the charge (i.e., higher charge density), the higher the energy of the system. Delocalizing charge is a stabilizing phenomenon because it reduces these electron-electron repulsions.
For kinetic energy, we previously used a “energy of confinement” model for wave-like electrons that predicts a lower kinetic energy when the electron wave is confined to a larger volume. When electrons are confined to the three-atom-π-bonding network of O3, they will have a lower kinetic energy than if they were confined to a single unhybridized 2p orbital (or a single π bond between two O atoms).
Thus, electron delocalization overall lowers the total energy of the system by lowering both potential energy and kinetic energy.
Activity: Molecular Structure of Resonance Hybrid
Some acid rain results from the reaction of sulfur dioxide with atmospheric water vapor, followed by the formation of sulfuric acid. Sulfur dioxide, SO2, is a major component of volcanic gases as well as a product of the combustion of sulfur-containing coal.
Determine the hybridization of the S atom in SO2. Draw a set of resonance structures for SO2 with correct molecular geometry; include all lone pairs and formal charges in your resonance structures.
Draw in your notebook, then left-click here for an explanation.
The major contributing resonance structures of sulfur dioxide are:

In both resonance structures, the sulfur atom has one single bond, one double bond, and one lone pair. Therefore, the hybridization of the sulfur atom is sp2, and the molecular geometry is bent. The lone pair resides in one of the sp2 hybrid orbitals, and the unhybridized 3p atomic orbital is involved in the delocalized π bonding.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

