D35.4 Polyprotic Acids
We can classify acids by the number of protons per molecule that they can donate in an acid-base reaction. Acids that contain one ionizable hydrogen atom per molecule are called monoprotic acids. Examples include HCl, HNO3, HCN, and CH3COOH. In the same vein, monoprotic bases are bases that can accept a single proton.
Diprotic acids contain two ionizable hydrogen atoms per molecule. For example:
HSO4–(aq) + H2O(ℓ) ⇌ SO42-(aq) + H3O+(aq) Ka,2 = 1.1 × 10-2
A triprotic acid, such as phosphoric acid, is an acid that has three protons that undergo stepwise dissociation:
H2PO4–(aq) + H2O(ℓ) ⇌ HPO42-(aq) + H3O+(aq) Ka,2 = 6.3 × 10-8
HPO42-(aq) + H2O(ℓ) ⇌ PO43-(aq) + H3O+(aq) Ka,3 = 4.6 × 10-13
The phosphate anion, PO43-, is an example of a triprotic base.
Notice that in both examples above, the dissociation of the first H+ takes place to a greater extent than the dissociation of the second H+, etc. (in other words, Ka,1 > Ka,2 > Ka,3). This is generally the case for polyprotic acids, although by how much Ka,2 is smaller than Ka,1 would vary acid to acid.
Let’s use phosphoric acid as an example to think about the successive dissociation steps in a little more detail.
| ΔrH° (kJ/mol) | ΔrS° (J/mol·K) | Ka (25 °C) | pKa (25 °C) |
|
| H3PO4(aq) + H2O(ℓ) ⇌ H2PO4–(aq) + H3O+(aq) | -8.3 | -68 | 7.2 × 10-3 | 2.14 |
| H2PO4–(aq) + H2O(ℓ) ⇌ HPO42-(aq) + H3O+(aq) | 4.2 | -124 | 6.3 × 10-8 | 7.20 |
| HPO42-(aq) + H2O(ℓ) ⇌ PO43-(aq) + H3O+(aq) | 14.7 | -187 | 4.6 × 10-13 | 12.34 |
Removing the first proton is exothermic—the energy required to break the O-H bond in H3PO4 and disrupt the H3PO4···water interaction is less than the energy released by forming the O-H bond in H3O+ and forming the ion-water interactions. However, there is an entropic penalty (ΔrS° is negative) stemming from the stronger ion-water interactions present in H2PO4¯(aq) and H3O+(aq). Together, this leads to an overall positive ΔrG° at 25 °C and a Ka < 1. (This is similar to HF.)
The second proton is removed from an already negatively charged H2PO4¯. In terms of ΔrH°, this is less favorable than removing the first proton—the product, HPO42-, contains two excess electrons, and this build up of excess charge destabilizes the conjugate base, making the acid less acidic. In fact, the second dissociation step is an endothermic process. It is also less favorable in terms of ΔrS° because the dianion’s interaction with water molecules is even stronger, leading to a larger shell of rigidly connected water molecules.
This trend continues for the third dissociation step.
In general, when all else are the same, it is easier (energetically more favorable) to remove an H+ from a positively charged molecule, and harder (energetically less favorable) to remove an H+ from a negatively charged molecule. Hence, Ka,1 > Ka,2 > Ka,3 for polyprotic acids.
Why is acetic acid, CH3COOH, not polyprotic?
What would the successive dissocation steps be?
CH3COOH(aq) + H2O(ℓ) ⇌ CH3COO–(aq) + H3O+(aq) Ka,1 = 1.8 × 10-5
CH3COO– + H2O(ℓ) ⇌ CH2COO2-(aq) + H3O+(aq) Ka,2 = ??
For us to consider the second step to be essentially not occurring, Ka,2 would have to be very very small. (after all, phosphoric acid’s Ka,3 = 4.6 × 10-13 and we consider phosphoric acid as triprotic.) Let’s draw the Lewis structures involved in the second step and think about why.

The bond that is broken is a C-H bond, which is not a particularly polar bond. The conjugate base has excess electron density localized on a C atom, which has a relatively low electronegativity.
Simply considering the two factors above, an ordinary alkane molecule would have essentially no acid strength. For example, the pKa of propane is ~50. However, the conjugate base above is even worse: it has a -2 charge. pKa,2 therefore would be quite a bit more than 50 (i.e., Ka,2 << 1 × 10-50). It is energetically more favorable for this molecule to fall apart than to form this dianion.
If the successive Ka‘s of a polyprotic acid differ by at least 20 times (pKa‘s differ by at least 1.3), it is OK to treat the dissociation steps as separate equilibria. This can simplify the math considerably because we can assume that the concentration changes from subsequent dissociation step(s) would not perturb the equilibrium of the first step. For an example, consider the activity below.
Activity: Ionization of a Diprotic Acid
There is another group of commonly occurring diprotic acids, called dicarboxylic acids. As the name suggest, each molecule contains two carboxylic acid groups, giving rise to its diprotic nature.
Oxalic acid is the simplest dicarboxylic acid, and occurs naturally in many foods, such as members of the spinach family and cabbage family, rhubarb, and many soil fungi.
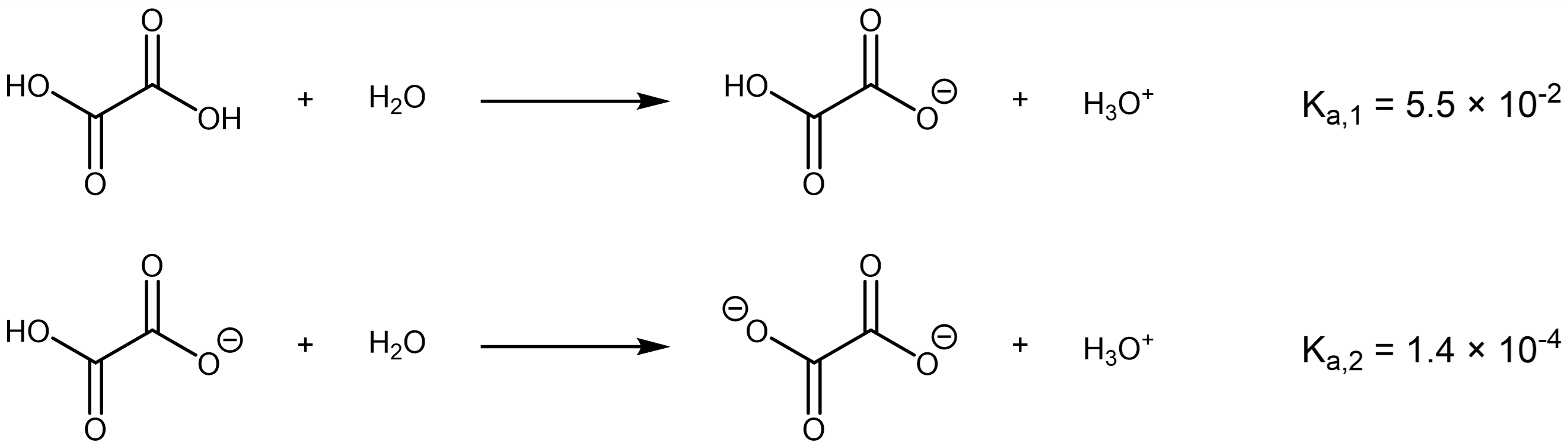
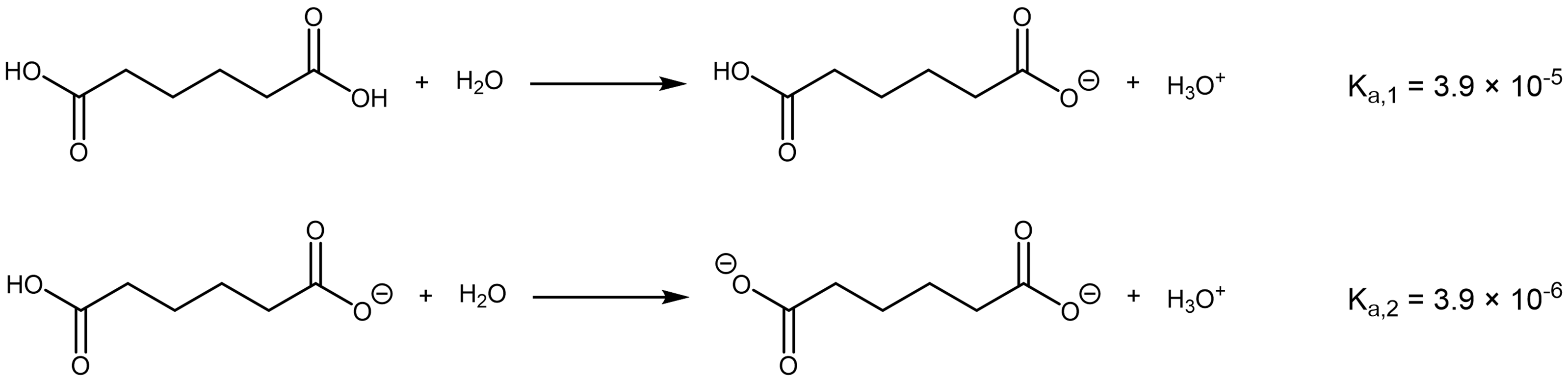
If the length of the alkyl chain connecting the two carboxylic acid groups is extended, the successive Ka values become closer to each other. For example, 1,6-hexanedioic acid, a reactant for making polyamides, has successive Ka‘s that differ by only 10 times (pKa‘s differ by 1.0).
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

