D24.2 Activation Energy

It is useful to examine reaction progress for the isomerization of cis-1,2-difluoroethene in more detail. As we saw previously, the angle of rotation around the double bond is a good measure of the progress of the reaction. Even a little rotation around the C=C double bond increases energy, because even a little rotation moves the atomic p orbital on one carbon atom out of exact side-by-side alignment with the p orbital on the other carbon atom, thereby partially breaking the π bond. Also, the direction of rotation does not matter, because rotating in either direction can lead to isomerization. Thus, we use angle of rotation to delineate the x-axis in a reaction energy diagram.

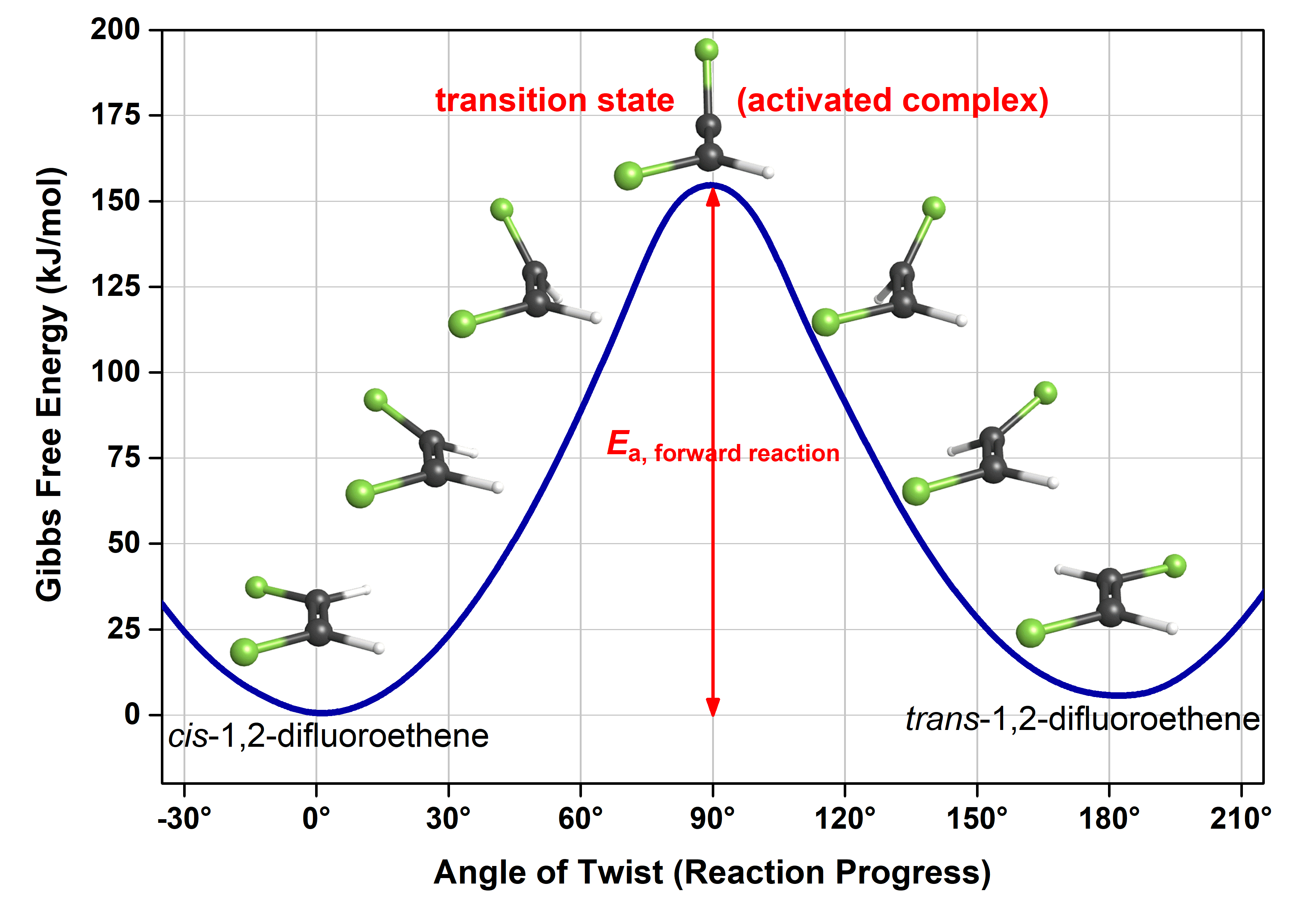
This figure is similar to the reaction energy diagram we saw earlier. The main difference is that the x-axis is defined to be angle of rotation and the y-axis has energy values. Note that while the x-axis of a reaction energy diagram is always “reaction progress”, the exact electron density rearrangments and atomic motions that connect reactants to products are unique to each reaction.

Let us use the more detailed reaction energy diagram to discuss a few crucial pieces of information. Here, the reactant (cis isomer) and product (trans isomer) are connected by a single transition state, which is a maximum on the reaction energy diagram. The transition-state structure (or activated complex) is the structure that corresponds to the transition state. Because a transition-state structure has greater energy than either reactant molecule(s) or product molecule(s), it is unstable relative to both. Moreover, it exists at a maximum on the reaction energy diagram (in comparison, the reactant and product exist at a minimum, usually different for reactant and product). The instability of the transition-state structure means that it exists for only a very short time (typically <10^-15 s), and it is very difficult to observe an activated complex experimentally.

The difference in energy between the transition state and the reactant(s) is the activation energy (E_a) of the forward reaction. Similarly, the difference in energy between the transition state and the product(s) is the E_a of the reverse reaction. Reading from the figure, the activation energy for the forward reaction is 158 kJ/mol (or 262 × 10^-21 J/molecule. If a cis-1,2-difluoroethene molecule has less than 158 kJ/mol, it cannot proceed to form trans-1,2-difluoroethene.

As we saw previously, there is a distribution of kinetic energies (and hence velocities) for individual molecules at a given temperature. The distributions of molecular energies for cis-1,2-difluoroethene gas molecules at various temperatures are shown below.

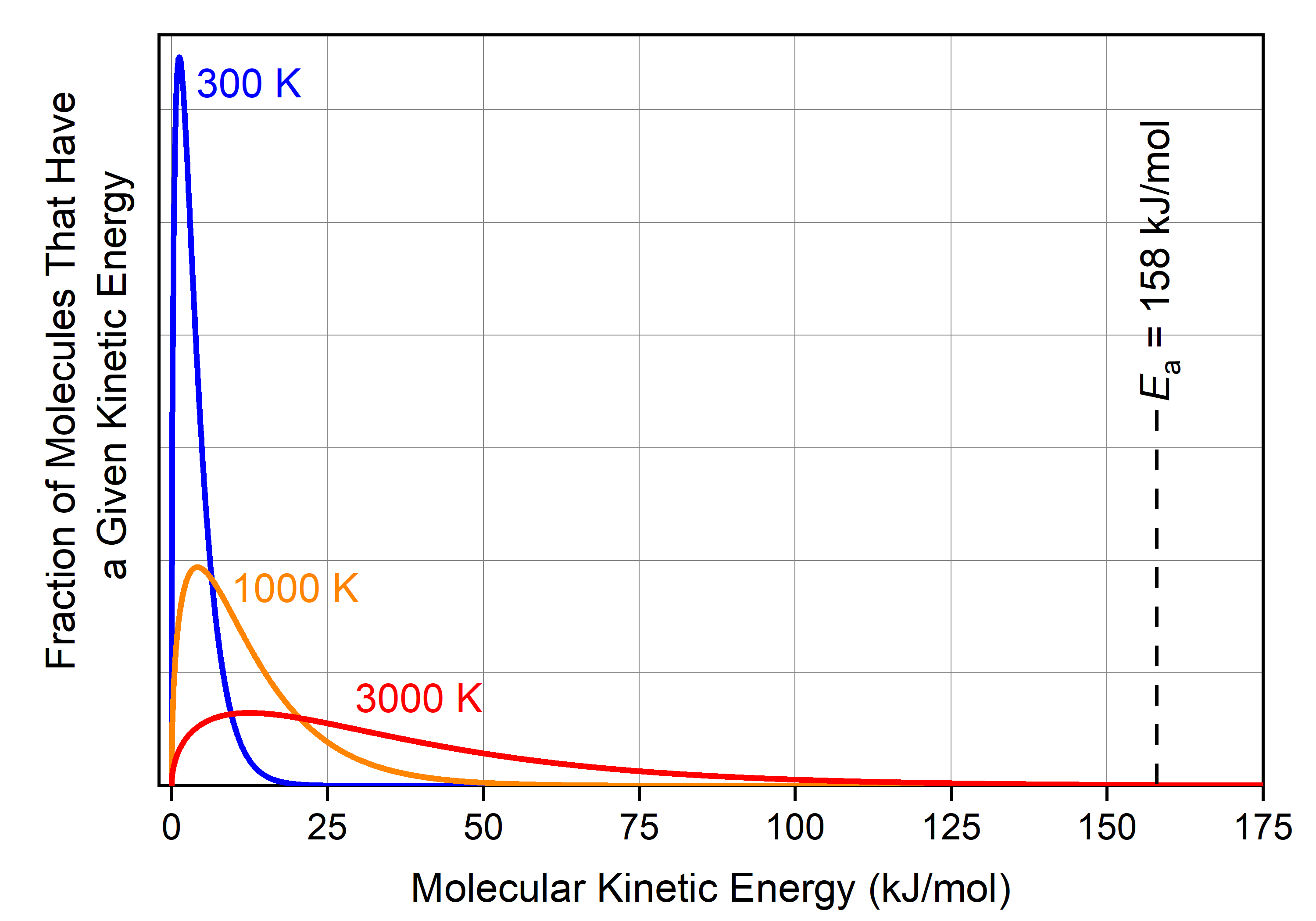
At 300 K, the fraction of cis-1,2-difluoroethene molecules with energy >158 kJ/mol (blue curve) is minuscule: you would need 35 kg of cis-1,2-difluoroethene to have 1 molecule that has KE > E_a. Therefore, there is essentially no cis-1,2-difluoroethene molecule with enough energy to reach the transition state at 300 K, and the reaction does not occur at this temperature (rate = 0; the time needed for a sample of cis-1,2-difluoroethene to reach equilibrium with trans-1,2-difluoroethene is hundreds of millions of years).

There are significantly more molecules with sufficient energy at 1000 K (orange curve): namely, 2 × 10¹⁶ cis-1,2-difluoroethene molecules in a 1 mole (0.064 kg) sample have KE > E_a. (This is not obvious in the graph because this fraction of molecules represents 0.000003% of the total molecules.) If one of these rapidly moving molecules hits another molecule in a way that causes one carbon to start rotating with respect to the other carbon, and if the collision is hard enough that the second molecule now has energy greater than E_a, then the cis isomer can transform into the trans isomer.

Remember that the cis-1,2-difluoroethene molecules are constantly colliding and exchanging energy with each other. If you could follow a specific molecule over time, you would see its kinetic energy continually changing; occasionally it will be part of the fraction with KE > E_a. This is true for all the molecules within the sample of cis-1,2-difluoroethene at 1000 K. Moreover, molecules are moving faster on average at 1000 K than at 300 K (KE_avg is greater). This leads to more frequent collisions and more frequent exchanges of energies. Therefore, the reaction rate is significantly faster at 1000 K, and equilibrium can be reached on the order of seconds.

At a given temperature, the equilibrium constant and its expression can be used to determine the equilibrium concentrations or partial pressures of products relative to reactants. However, it does not tell us how fast equilibrium is reached. Chemical kinetics is the study of rates of reactions and provides this vital information. Both kinetics and thermodynamics are needed to characterize a chemical reaction because a useful reaction usually is one where significant quantities of products can be produced in a short time.