D17.1 Energy and Phase Change
Earlier we used boiling points of substances as a way to compare the strengths of attractive forces between molecules (London forces (LDFs), dipole-dipole forces, hydrogen bonds). We now explore that idea in more detail.
When a liquid boils, molecules become much farther apart in the gas phase than they were in the liquid phase. Because of intermolecular attractive forces, the energy of a pair of molecules is lower when the molecules are close together than when they are farther apart. For example, consider argon, which boils at 87.3 K (−185.8 °C). The figure in the activity below shows how the potential energy of two argon atoms varies with distance between their atomic nuclei.
Activity: Analysis of Potential Energy Curve for Argon
Look carefully at the potential energy curve for argon shown below. The curve has a minimum at a distance of 377 pm and an energy of -1.16 kJ/mol.
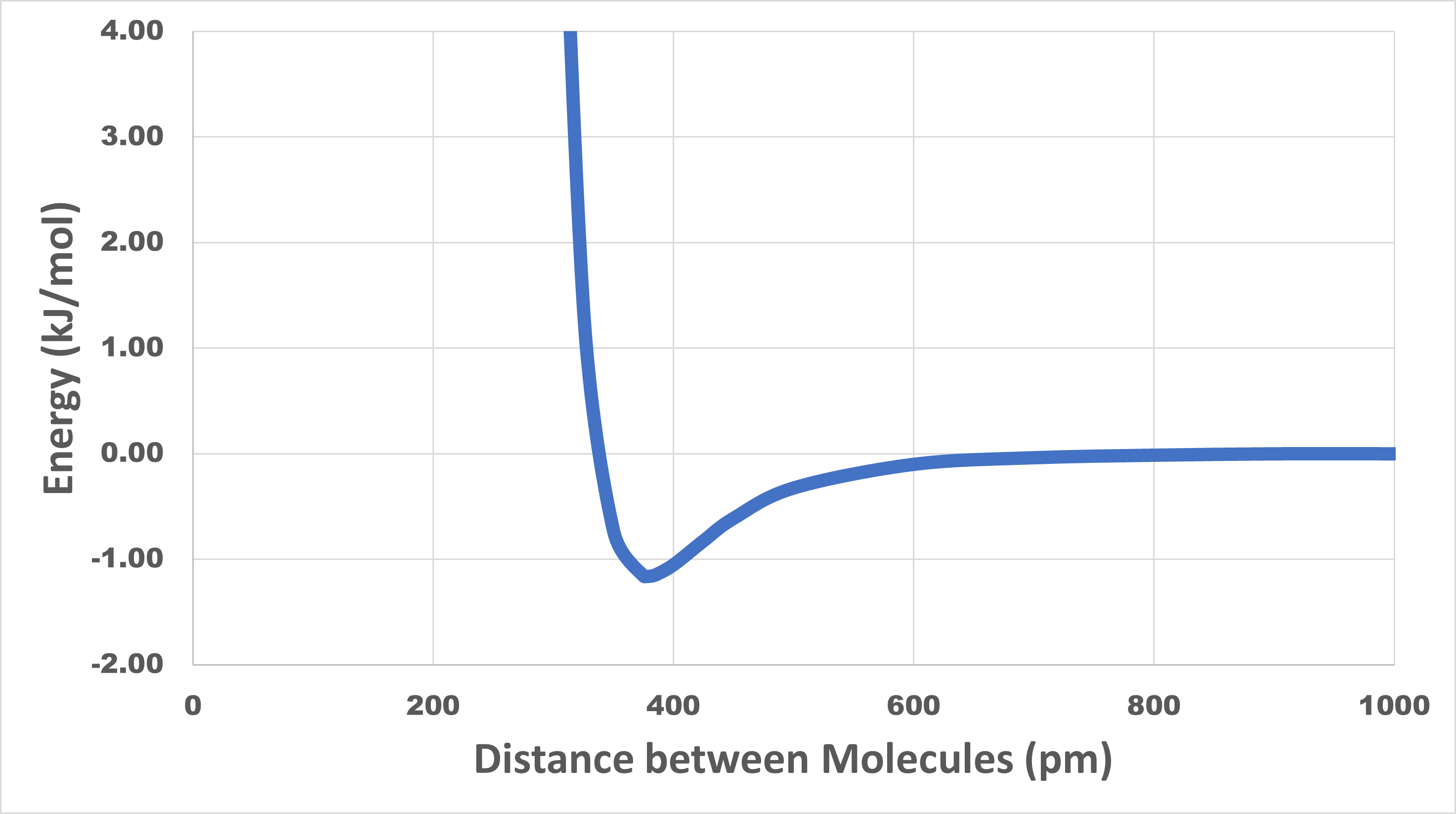
Why does the curve go up rapidly at distances less than 350 pm?
Another student says that the LDFs between argon atoms are short-range forces and are not important at distances greater than 600-800 pm. Use data from the figure to support or argue against this statement and write down your reasoning.
Write in your notebook, then left-click here for an explanation.
The minimum energy value of -1.16 kJ/mol indicates that an energy of 1.16 kJ/mol is required to separate two argon atoms that are initially 377 pm apart.
The curve goes up rapidly at distances less than 350 pm because such distances correspond to superimposing two argon atoms. Because the electron clouds of each atom are being forced together, the mutual repulsions among electrons cause the energy to increase rapidly.
The statement that LDFs are short-range forces is supported by the data. At distances greater than 800 pm the potential energy values are essentially zero, which means there is no attractive force between the molecules. (In this case the molecules are argon atoms, but this applies to LDFs between any pair of molecules.) LDFs drop off very rapidly as molecules move farther apart.
Now think about what happens when argon boils. In the gas phase, nearly all the molecules are much farther apart than 800 pm, so the attractions between them are negligible. In the liquid phase, the molecules are 350–450 pm apart and almost every molecule is surrounded by many other molecules at distances less than 600 pm. Separating two molecules requires that the molecules have at least enough kinetic energy to go from −1.16 kJ/mol on the potential energy curve (distance of 377 pm) to 0 kJ/mol on the curve (distance of >800 pm). For a pair of molecules 377 pm apart, 1.16 kJ/mol (or 1.93 × 10-21 J per molecule) is required to separate the molecules. At any given instant, each molecule in the liquid is surrounded by about a dozen other molecules at distances ranging between 350 and 450 pm. The situation is more complicated than for just two molecules and the energy required is greater: it takes 6.4 kJ/mol (or 1.06 x 10−20 J per molecule) to vaporize a sample of liquid argon.
The energy of all the molecules in 1 mol gaseous argon is 6.4 kJ greater than the energy the molecules had in the liquid phase at the same temperature. This difference is the result of attractive forces (London dispersion forces) that cause the energies of molecules that are close together in the liquid phase to be less than the energies of molecules that are far apart in the gas phase. It follows from the law of conservation of energy (also called the first law of thermodynamics) that, because the energy of the gas-phase molecules is greater than the energy of the liquid-phase molecules, energy must be transferred to the argon from somewhere else as the argon vaporizes.
Distribution of Molecular Energies
Activity: Molecular Speeds in Argon Gas
The video above is an atomic-scale simulation of a small portion of a sample of argon gas at 189 K. (Source: PHET simulations: States of Matter.)
Observe the simulation carefully. Compare the speeds of different molecules. Also, watch one molecule and follow its motion. Write at least two observations about the motion of the molecules shown in the video.
Write in your notebook, then left-click here for an explanation.
Here are four possible observations. There may be more or these might be worded differently.
- The video shows that molecules of argon (Ar atoms) are in constant motion.
- Not all molecules are moving at the same speed. At any instant some molecules are moving very fast and some are much slower.
- A single Ar molecule moves slowly at some times but at other times it moves much faster.
- Collisions with other molecules can change the speed and direction at which a molecule moves.
As you can see from the simulation of argon gas, molecules are in constant motion. At a given instant, some molecules are moving fast and others are moving slowly. That is, there is a distribution of speeds of the molecules. Because kinetic energy is proportional to the square of molecular speed, there is also a distribution of molecular energies: some molecules have much greater energies than others. The temperature of a sample of matter is proportional to the average energy over all these different molecular energies.
When a sample of liquid argon boils, bubbles of argon gas form within the liquid and rise to the surface. (The same applies to boiling water or any other liquid.) Consider a single argon atom (or a single molecule of any liquid). In both liquid and gas the energy of any individual molecule changes continually as a result of collisions with other molecules: sometimes the molecule’s energy is low, sometimes it is high. If an argon molecule’s energy is equal to or higher than 6.4 kJ/mol, the molecule has enough energy to overcome the attractions toward other molecules that surround it; if the molecule is at the surface of the liquid, then it can transfer from liquid phase to gas phase. However, only those molecules with sufficient energy can escape; that is, only high-energy molecules transfer from liquid to gas phase.
Activity: Molecular Energies and Phase Changes
Based on what you have just read, write a few sentences in response to each prompt.
- Use scientifically appropriate language to explain why a liquid can evaporate to form a gas even though the temperature is below the boiling point. (For example, a puddle of water on a paved street evaporates when the temperature is 20 °C.)
- When you perspire, evaporation of perspiration (mostly water) cools your skin. Explain why the water that remains on your skin is cooler after some water has evaporated.
Write in your notebook, then left-click here for an explanation.
- Because there is a broad range of molecular energies, even at temperatures below the boiling point, a few molecules in a liquid have much higher than average energies–energies large enough for the molecule to overcome the attractions of surrounding molecules. Such molecules can transfer from liquid to gas phase, which corresponds to evaporation at the macroscale.
- When some high-energy molecules transfer from liquid to gas phase, the average energy of the molecules remaining in the liquid decreases. Because the average energy of the molecules is proportional to temperature, the temperature of the remaining liquid must also be lower, and the liquid is cooler.
This question did not ask why evaporation cools your skin, but that’s important in keeping you cool, so let’s think about it. As soon as the liquid becomes cooler than your skin, energy transfers from your skin to the liquid. Where the liquid contacts your skin, molecules of liquid (which have lower average kinetic energy) contact molecules that make up your skin (which have higher average kinetic energy). This contact allows energy to transfer, driving the two (liquid and skin) toward having the same average kinetic energy. As the total quantity of energy in your skin decreases during this process, the average energy of skin molecules decreases and so the temperature decreases. We will say more about this transfer of energy from a warmer object to a cooler one in the next section.
During our discussion of boiling argon, you may have thought, “How did someone find out that it takes 6.4 kJ/mol to separate argon molecules from liquid to gas phase?” Such information is obtained by measurements that involve instruments known as calorimeters. The next section explores such measurements in more detail.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

