D38.2 Titration Curves
The acid-base reactions that we have discussed thus far are commonly employed for titration because there is a rapid change in solution pH near the equivalence point in these titrations. This means that there would be a clear observable change accompanying a small addition of titrant, which minimizes experimental uncertainty. For example, an acid-base indicator generally changes color over a range of about 2 pH units, so if pH increases (or decreases) by 2 or more pH units when 0.01 mL of titrant is added at the equivalence point, the color change would effectively signal the end point of the titration.
In typical acid-base titrations, a strong acid or a strong base is used in one of the solutions to ensure that the resulting acid-base reaction is heavily product-favored (essentially goes to completion).
The figure below shows a titration curve, a graph of pH as a function of volume of titrant, for the titration of a 50.00-mL sample of 0.100-M hydrochloric acid with 0.100-M sodium hydroxide.
Exercise: Titration Curve
A titration is carried out for 50.00 mL of 0.100 M HCl with 0.100 M NaOH at 25 °C. The titration curve is shown above in Figure: Titration curve (HCl and NaOH).
What is the dominant species in the reaction solution (in the flask) when the following volumes of NaOH are added?
- 0.00 mL
- 25.00 mL
- 50.00 mL
- 60.00 mL
Write in your notebook, then left-click here for an explanation.
- With no NaOH added, the flask contains only the HCl solution. Because HCl is a strong acid, it is fully dissociated in solution, and the dominant species in the solution are H3O+(aq) and Cl¯(aq).
- Cl¯ does not have any acidity or basicity, so the solution pH is dictated by the concentration of H3O+ present.
- pH = −log[H3O+] = −log(0.100) = 1.000
- Cl¯ does not have any acidity or basicity, so the solution pH is dictated by the concentration of H3O+ present.
- NaOH is a strong base, it dissociates in solution to yield Na+(aq) and OH¯(aq). When NaOH is added from the buret to the flask, OH¯ readily reacts with H3O+ that are present in the HCl solution. The reaction is:
HCl(aq) + NaOH(aq) ⇌ NaCl(aq) + H2O(ℓ)
- In the original 50.00 mL of 0.100M HCl solution, there are (0.100 M)(0.05000L) = 0.00500 mol of H3O+ present.
- When 25.00 mL of 0.100 M NaOH is added, (0.100 M)(0.02500L) = 0.00250 mol of OH¯ reacts with the H3O+ present.
- This leaves 0.00500 mol - 0.00250 mol = 0.00250 mol H3O+ (in other words, at 25.00 mL NaOH added, HCl is the excess reactant.)
All of the added OH¯ have reacted away, this leaves in solution H3O+(aq), Cl¯(aq), and Na+(aq).
- Cl¯ and Na+ do not have any acidity or basicity, so the solution pH is dictated by the concentration of H3O+ present.
- [latex]pH = - \log [\text{H}_3\text{O}^+] = - \log \left(\dfrac{0.00250\;mol}{0.05000\;L\;+\;0.02500\;L}\right) = 1.478[/latex]
- The equivalence point is reached when a total of 50.00 mL of NaOH is added. At the equivalence point, the acid-base reaction is complete with no excess reactants left, this means the dominant species in solution are Cl¯(aq), and Na+(aq).
- The amount of H3O+ and OH¯ present are from the water autoionization process.
- When a total of 60.00 mL of NaOH is added, there would be an excess of NaOH. All of the H3O+ have reacted away, this leaves in solution OH¯(aq), Cl¯(aq), and Na+(aq).
- The solution pH is dictated by the concentration of OH¯ present.
- (0.100 M)(0.06000L NaOH) - (0.100 M)(0.05000L HCl) = 0.00100 mol OH¯
- [latex]pH = 14 - pOH = 14 + \log \left(\dfrac{0.00100\;mol}{0.05000\;L\;+\;0.06000\;L}\right) = 11.959[/latex]
- The solution pH is dictated by the concentration of OH¯ present.
Now let's consider the titration of 50.00 mL of 0.100 M acetic acid with 0.100 M sodium hydroxide, titration curve shown below.
Comparing it to the one for HCl and NaOH, we see that although the initial volumes and concentrations of the acids are the same, the solution pH for acetic acid begins at a higher value and the titration curve maintains higher pH values up to the equivalence point. This is because acetic acid is a weak acid that only partially dissociates in solution.
At the equivalence point, the pH is also higher (8.72 rather than 7.00). This is because the dominant species present in solution at the equivalence point is Na+ and CH3COO¯, the latter is a weak base that raises the pH via the reaction:
After the equivalence point, the two titration curves are identical because the pH depends on the excess NaOH added.
Activity: Titration Equivalence Point
"For titration of a series of weak acids with a strong base, the weaker the acid being titrated is, the higher the pH value at the equivalence point."
This statement is true under certain conditions. Explain why the statement is true and state the conditions needed to make it true.
Write in your notebook, then left-click here for an explanation.
The statement is true if the concentrations of the weak acids are the same and the concentration of the titrant (strong base) is the same. Also, all titrations must be carried out at the same temperature.
At the equivalence point, the solution contains the conjugate base of the weak acid. The weaker an acid is the stronger its conjugate base is. For a given concentration and temperature, the stronger base would have a higher pH, so the titration of the same initial concentration of a weaker acid with the same concentration of strong base has a more alkaline (higher pH) equivalence point.
The midpoint of a titration is when half the volume of titrant needed to reach the equivalence point has been added. When titrating a weak acid with a strong base, the pH of the solution at midpoint equals the pKa of the weak acid. This is because when exactly half the amount of strong base needed is added, the concentration of the weak acid present in the solution is equal to the concentration of its conjugate base:
Activity: Titration of a Weak Base with a Strong Acid
Consider the titration of 50.00 mL of 0.100-M ammonia (NH3, Kb = 1.77 × 10−5) with 0.100-M hydrochloric acid (HCl) at 25 °C. Write the balanced chemical equation for the titration reaction. Without calculating any concentrations, sketch the titration curve for this titration. Explain how you estimated the pH halfway to the equivalence point. Is the pH at the equivalence point greater than or less than 7? Estimate the pH after a large excess of HCl has been added.
On the same axes, sketch a titration curve for titration of 50.00 mL of 0.100-M sodium bicarbonate (NaHCO3, Kb = 2.3 × 10−8) with 0.100-M hydrochloric acid (HCl). Describe how this titration curve differs from the titration curve for ammonia. For each difference, explain why the curve is different.
Sketch two titration curves, then left-click here for an explanation.
The equation for the first titration (red curve in figure below) is
NH3(aq) + HCl(aq) ⇌ NH4Cl(aq)
Because ammonia is a weak base, the titration curve begins at pH > 7 but well below the pH of 0.1-M strong base (which is pH = 13).
Halfway to the equivalence point, when 25.00 mL HCl has been added, pH = pKa for the conjugate acid of ammonia. pKb for ammonia is
−log(1.77 × 10−5) = 4.752
and, for ammonium ion,
pKa = 14 − 4.752 = 9.248
Thus, halfway to the equivalence point the pH should be a little above 9.
At the equivalence point all the ammonia has been converted to its conjugate acid, ammonium ion. This weak acid causes the pH to be less than 7.
After an excess of HCl has been added, the pH is determined solely by the concentration of strong acid. Therefore the pH decreases toward a minimum value of −log(0.100) = 1.0. (If 10 L of 0.100-M HCl were added to the titration solution, the HCl would hardly be diluted by the small volume of base solution initially present, and the concentration of hydronium ions would approach 0.100 M.)
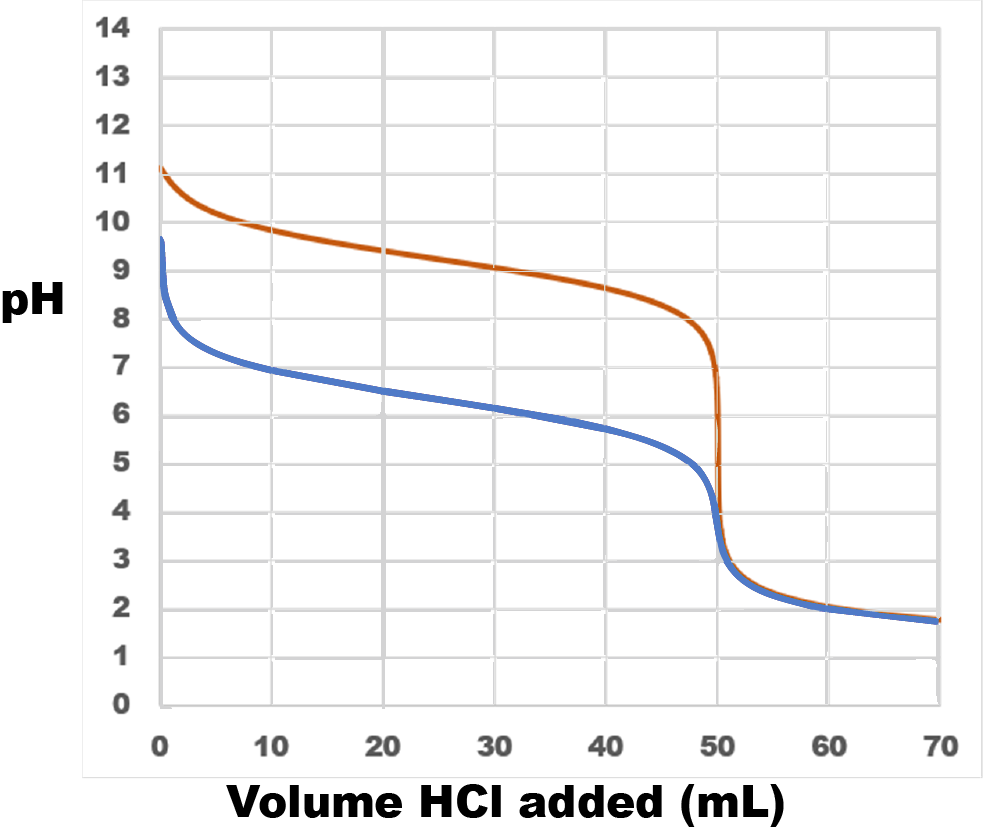
Bicarbonate is an amphiprotic species. Adding strong acid causes it to act as a base. The overall reaction is:
NaHCO3(aq) + HCl(aq) ⇌ H2CO3(aq) + NaCl
Because the Kb for bicarbonate ion is smaller, it is a weaker base than ammonia. Consequently, the titration curve (blue curve in figure above) is lower on the pH scale. pKa for carbonic acid, H2CO3, the conjugate acid of bicarbonate ion, is 14 − (−log(2.3 × 10−8)) = 6.36, so at the midpoiont of the titration the pH = 6.36.
Because bicarbonate is a weaker base than ammonia, its conjugate acid H2CO3 is a stronger acid than ammonium ion. Therefore the equivalence point (where all the bicarbonate ion has been converted to carbonic acid) has a lower pH than the equivalence point for the ammonia titration.
Once the equivalence point has been reached, the titration curve is exactly the same for both titrations because the pH depends only on the amount of HCl and the solution volume and those are the same in both cases.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

