2 Isotopes and Atomic Mass

Learning Objectives

  • Recognize that elements are identified by the number of protons, but the number of neutrons may vary (isotopes).
    | Isotopes |
  • Calculate natural abundance and atomic mass.
    | Natural Abundance |

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Isotopes

Although all atoms of an element exhibit similar behavior, they are not all the same. The symbol for a specific isotope of any element is written by placing the mass number as a superscript to the left of the element symbol (Figure 1). The atomic number is sometimes written as a subscript preceding the symbol, but since this number defines the element’s identity, as does its symbol, it is often omitted. For example, magnesium exists as a mixture of three isotopes, each with an atomic number of 12 and with mass numbers of 24, 25, and 26, respectively. These isotopes can be identified as 24Mg, 25Mg, and 26Mg. These isotope symbols are read as “element, mass number” and can be symbolized consistent with this reading. For instance, 24Mg is read as “magnesium 24,” and can be written as “magnesium-24” or “Mg-24.” 25Mg is read as “magnesium 25,” and can be written as “magnesium-25” or “Mg-25.” All magnesium atoms have 12 protons in their nucleus. They differ only because a 24Mg atom has 12 neutrons in its nucleus, a 25Mg atom has 13 neutrons, and a 26Mg has 14 neutrons.

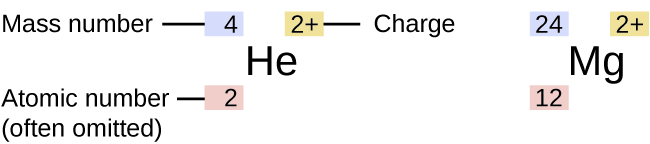
This diagram shows the symbol for helium, “H e.” The number to the upper left of the symbol is the mass number, which is 4. The number to the upper right of the symbol is the charge which is positive 2. The number to the lower left of the symbol is the atomic number, which is 2. This number is often omitted. Also shown is “M g” which stands for magnesium It has a mass number of 24, a charge of positive 2, and an atomic number of 12.
Figure 1. The symbol for an atom indicates the element via its usual two-letter symbol, the mass number as a left superscript, the atomic number as a left subscript (sometimes omitted), and the charge as a right superscript.

Information about the naturally occurring isotopes of elements with atomic numbers 1 through 10 is given in Table 1. Note that in addition to standard names and symbols, the isotopes of hydrogen are often referred to using common names and accompanying symbols. Hydrogen-2, symbolized 2H, is also called deuterium and sometimes symbolized D. Hydrogen-3, symbolized 3H, is also called tritium and sometimes symbolized T.

Element Symbol Atomic Number Number of Protons Number of Neutrons Mass (amu) % Natural Abundance
hydrogen [latex]_1^1[/latex]H (protium) 1 1 0 1.0078 99.989
[latex]_1^2[/latex]H (deuterium) 1 1 1 2.0141 0.0115
[latex]_1^3[/latex]H (tritium) 1 1 2 3.01605 — (trace)
helium [latex]_2^3[/latex]He 2 2 1 3.01603 0.00013
[latex]_2^4[/latex]He 2 2 2 4.0026 100
lithium [latex]_3^6[/latex]Li 3 3 3 6.0151 7.59
[latex]_3^7[/latex]Li 3 3 4 7.0160 92.41
beryllium [latex]_4^9[/latex]Be 4 4 5 9.0122 100
boron [latex]_5^{10}[/latex]B 5 5 5 10.0129 19.9
[latex]_5^{11}[/latex]B 5 5 6 11.0093 80.1
carbon [latex]_6^{12}[/latex]C 6 6 6 12.0000 98.89
[latex]_6^{13}[/latex]C 6 6 7 13.0034 1.11
[latex]_6^{14}[/latex]C 6 6 8 14.0032 — (trace)
nitrogen [latex]_7^{14}[/latex]N 7 7 7 14.0031 99.63
[latex]_7^{15}[/latex]N 7 7 8 15.0001 0.37
oxygen [latex]_8^{16}[/latex]O 8 8 8 15.9949 99.757
[latex]_8^{17}[/latex]O 8 8 9 16.9991 0.038
[latex]_8^{18}[/latex]O 8 8 10 17.9992 0.205
fluorine [latex]_9^{19}[/latex]F 9 9 10 18.9984 100
neon [latex]_{10}^{20}[/latex]Ne 10 10 10 19.9924 90.48
[latex]_{10}^{21}[/latex]Ne 10 10 11 20.9938 0.27
[latex]_{10}^{22}[/latex]Ne 10 10 12 21.9914 9.25
Table 1. Nuclear Compositions of Atoms of the Very Light Elements

Demonstration: Heavy water is more dense than regular water

Set up. As shown in the table above, hydrogen and oxygen each have three isotopes. Of these isotopes, hydrogen-1 and oxygen-16 are by far the most common isotopes. Therefore, water molecules typically consist of two hydrogen-1 atoms and an oxygen-16 atom, giving a molecular weight of ~18 amu. It is possible to form “heavy water”—water that is composed of two hydrogen-2 atoms and an oxygen-16 atom. This heavy water has a molecular weight of ~20 amu. In this demonstration, we compare the density of solid regular water (regular ice) and solid heavy water (“heavy water ice”) by placing each into a glass of liquid regular water.

Prediction. Before watching the video, make a prediction about whether the heavy water ice will float or sink in the glass of liquid water.

Explanation. In this video, the regular ice floats on the liquid regular water, as expected for an ice cube in a glass of water because the density of solid (regular) water is less than the density of liquid (regular) water. However, the heavy water ice cube sinks to the bottom of the glass because the extra mass causes the density of the heavy water ice to be greater than the density of the liquid regular water, and therefore it is unable to float.

 

Use this Build an Atom simulator to build atoms of the first 10 elements, see which isotopes exist, check nuclear stability, and gain experience with isotope symbols.

Natural Abundance

Because each proton and each neutron contribute approximately one amu to the mass of an atom, and each electron contributes far less, the atomic mass of a single atom is approximately equal to its mass number (a whole number). However, the average masses of atoms of most elements are not whole numbers because most elements exist naturally as mixtures of two or more isotopes.

The mass of an element shown in a periodic table or listed in a table of atomic masses is a weighted, average mass of all the isotopes present in a naturally occurring sample of that element. This is equal to the sum of each individual isotope’s mass multiplied by its fractional abundance.

average mass  =  ∑i (fractional abundance × isotopic mass)i

For example, the element boron is composed of two isotopes: About 19.9% of all boron atoms are 10B with a mass of 10.0129 amu, and the remaining 80.1% are 11B with a mass of 11.0093 amu. The average atomic mass for boron is calculated to be:

boron average mass  =  (0.199 × 10.0129 amu) + (0.801 × 11.0093 amu)
=  1.99 amu + 8.82 amu
=  10.81 amu

It is important to understand that no single boron atom weighs exactly 10.8 amu; 10.8 amu is the average mass of all boron atoms, and individual boron atoms weigh either approximately 10 amu or 11 amu.

Example 1

Calculation of Average Atomic Mass
A meteorite found in central Indiana contains traces of the noble gas neon picked up from the solar wind during the meteorite’s trip through the solar system. Analysis of a sample of the gas showed that it consisted of 91.84% 20Ne (mass 19.9924 amu), 0.47% 21Ne (mass 20.9940 amu), and 7.69% 22Ne (mass 21.9914 amu). What is the average mass of the neon in the solar wind?

Solution

neon average mass  =  (0.9184 × 19.9924 amu) + (0.0047 × 20.9940 amu) + (0.0769 × 21.9914 amu)
=  (18.36 + 0.099 + 1.69) amu
=  20.15 amu

The average mass of a neon atom in the solar wind is 20.15 amu. (The average mass of a terrestrial neon atom is 20.1796 amu. This result demonstrates that we may find slight differences in the natural abundance of isotopes, depending on their origin.)

Check Your Learning
A sample of magnesium is found to contain 78.70% of 24Mg atoms (mass 23.98 amu), 10.13% of 25Mg atoms (mass 24.99 amu), and 11.17% of 26Mg atoms (mass 25.98 amu). Calculate the average mass of a Mg atom.

Answer:

24.31 amu

We can also do variations of this type of calculation, as shown in the next example.

Example 2

Calculation of Percent Abundance
Naturally occurring chlorine consists of 35Cl (mass 34.96885 amu) and 37Cl (mass 36.96590 amu), with an average mass of 35.453 amu. What is the percent composition of Cl in terms of these two isotopes?

Solution
The average mass of chlorine is the fraction that is 35Cl times the mass of 35Cl plus the fraction that is 37Cl times the mass of 37Cl.

chlorine average mass  =  (fraction of 35Cl × mass of 35Cl) + (fraction of 37Cl × mass of 37Cl)

If we let x represent the fraction that is 35Cl, then the fraction that is 37Cl is represented by 1.00 − x.

(The fraction that is 35Cl + the fraction that is 37Cl must add up to 1, so the fraction of 37Cl must equal 1.00 − the fraction of 35Cl.)

Substituting this into the average mass equation, we have:

35.453 amu  =  (x × 34.96885 amu) + [(1.00 – x) × 36.96590 amu]
35.453  =  34.96885x + 36.96590 – 36.96590x
1.99705x  =  1.513
x  =  [latex]\frac{\text{1.513}}{\text{1.99705}}[/latex]  =  0.7576

So solving yields: x  =  0.7576, which means that 1.00 − 0.7576  =  0.2424. Therefore, chlorine consists of 75.76% 35Cl and 24.24% 37Cl.

Check Your Learning
Naturally occurring copper consists of 63Cu (mass 62.9296 amu) and 65Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What is the percent composition of Cu in terms of these two isotopes?

Answer:

69.15% Cu-63 and 30.85% Cu-65


Visit this site to make mixtures of the main isotopes of the first 18 elements, gain experience with average atomic mass, and check naturally occurring isotope ratios using the Isotopes and Atomic Mass simulation.

Key Concepts and Summary

Isotopes of an element are atoms with the same atomic number but different mass numbers; isotopes of an element, therefore, differ from each other only in the number of neutrons within the nucleus. When a naturally occurring element is composed of several isotopes, the atomic mass of the element represents the average of the masses of the isotopes involved.

Key Equations

  • average mass  =  ∑i (fractional abundance × isotopic mass)i

Glossary

atomic mass
average mass of atoms of an element, expressed in amu
empirical formula
formula showing the composition of a compound given as the simplest whole-number ratio of atoms
isotopes
atoms that contain the same number of protons but a different number of neutrons
molecular formula
formula indicating the composition of a molecule of a compound and giving the actual number of atoms of each element in a molecule of the compound

Chemistry End of Section Exercises

Isotopes

  1. Visit the PhET Isotopes and Atomic Mass simulation site and select the “Mix Isotopes” tab, hide the “Percent Composition” and “Average Atomic Mass” boxes, and then select the element boron.
    1. Write the symbols of the isotopes of boron that are shown as naturally occurring in significant amounts.
    2. Predict the relative amounts (percentages) of these boron isotopes found in nature. Explain the reasoning behind your choice.
    3. Add isotopes to the black box to make a mixture that matches your prediction in (b). You may drag isotopes from their bins or click on “More” and then move the sliders to the appropriate amounts.
    4. Reveal the “Percent Composition” and “Average Atomic Mass” boxes. How well does your mixture match with your prediction? If necessary, adjust the isotope amounts to match your prediction.
    5. Select “Nature’s mix” of isotopes and compare it to your prediction. How well does your prediction compare with the naturally occurring mixture? Explain. If necessary, adjust your amounts to make them match “Nature’s” amounts as closely as possible.
  2. Pick an element from this list of isotope abundances that has three naturally occurring isotopes, and find the average mass of the element given the abundances of its isotopes.

Natural Abundance

  1. Average atomic masses listed by IUPAC are based on a study of experimental results. Bromine has two isotopes 79Br and 81Br, whose masses (78.9183 and 80.9163 amu) and abundances (50.69% and 49.31%) were determined in earlier experiments. Calculate the average atomic mass of bromine based on these experiments.
  2. Variations in average atomic mass may be observed for elements obtained from different sources. Lithium provides an example of this. The isotopic composition of lithium from naturally occurring minerals is 7.5% 6Li and 92.5% 7Li, which have masses of 6.01512 amu and 7.01600 amu, respectively. A commercial source of lithium, recycled from a military source, was 3.75% 6Li (and the rest 7Li). Calculate the average atomic mass values for each of these two sources.
  3. The 18O:16O abundance ratio in some meteorites is greater than that used to calculate the average atomic mass of oxygen on earth. Is the average mass of an oxygen atom in these meteorites greater than, less than, or equal to that of a terrestrial oxygen atom?

Answers to Chemistry End of Section Exercises

  1. (a) 10B and 11B; (b) Boron has an average atomic mass of that is closer to 11 amu than 10 amu, so there should be more 11B than 10B. For example, we can estimate 65% 11B and 35% 10B; (c) check; (d) Average atomic mass of the example estimation is 10.661 amu; (e) the example estimation is off; nature’s mix is 80.1% 11B and 19.9% 10B with average atomic mass of 10.811 amu.
  2. Let us use neon as an example. Since there are three isotopes, there is no way to be sure to accurately predict the abundances to make the total of 20.18 amu average atomic mass. Let us guess that the abundances are 9% Ne-22, 91% Ne-20, and only a trace of Ne-21. The average mass would be 20.18 amu. Checking the nature’s mix of isotopes shows that the abundances are 90.48% Ne-20, 9.25% Ne-22, and 0.27% Ne-21, so our guessed amounts have to be slightly adjusted.
  3. 79.90 amu
  4. From natural source: 6.94 amu; from commercial source: 6.98 amu
  5. The average mass of an oxygen atom in meteroites is greater than the average mass of a terrestrial oxygen atom because there is more O-18 that occurs in a meterorite than does on earth.

 

License

Pharmacy Resource Book Copyright © by treitz. All Rights Reserved.

Share This Book