Part II. Our first agent-based evolutionary model
II-4. Interactivity and efficiency
1. Goal
Our goal in this chapter is to improve the interactivity and the efficiency of our model.
By interactivity we mean the possibility of changing the value of parameters at runtime, with immediate effect on the dynamics of the model. This feature is very convenient for exploratory work. In this chapter, we will implement the necessary functionality to let the user change the number of agents in the population at runtime.
By efficiency we mean implementing the model in such a way that it can be executed using as little time and memory as possible. In this chapter, we will modify the code of our model slightly to make it run significantly faster.
Oftentimes there is a trade-off between interactivity and efficiency: making the model more interactive generally implies some loss of efficiency. Nonetheless, sometimes we can find ways of implementing a model more efficiently without compromising its interactivity.
It is also important to be aware that –most often– there is also a trade-off between efficiency and code readability. The changes required to make our model run faster will frequently make our code somewhat less readable too. Uri Wilensky –the creator of NetLogo– and William Rand do not recommend making such comprises:
However, it is important that your code be readable, so others can understand it. In the end, computer time is cheap compared to human time. Therefore, it should be noted that, whenever there is a possibility of trade-off, clarity of code should be preferred over efficiency. Wilensky and Rand (2015, pp 219–20)
Our personal opinion is that this decision is best made case by case, taking into account the objectives and constraints of the whole modelling exercise in the specific context at hand. Our hope is that, after reading this book, you will be prepared to make these decisions by yourself in any specific situation you may encounter.
2. Motivation. The impact of population size
The dynamics of many evolutionary models strongly depend on the number of agents in the population. Can you guess how the population size affects the dynamics of the imitate-if-better decision rule with noise in the Rock-Paper-Scissors game? In this chapter we will implement the possibility of changing the population size at runtime, a feature that will greatly facilitate the exploration of this question.
3. Description of the model
We will not make any modification on the formal model our program implements. Thus, we refer to the previous chapter to read the description of the model. The only paragraph we add (about the program itself) is the following:
The number of players in the simulation can be changed at runtime with immediate effect on the dynamics of the model, using parameter n-of-players:
- If n-of-players is reduced, the necessary number of (randomly selected) players are killed.
- If n-of-players is increased, the necessary number of (randomly selected) players are cloned.
Thus, the proportions of agents playing each strategy remain the same on average (although the actual effect of this change is stochastic).
 4. Interactivity
4. Interactivity
Note that we can already modify the value of parameters prob-revision and noise at runtime, with immediate effect on the dynamics of the model. This is so because the values of these variables are used directly in the code. Parameter prob-revision is used only in procedure to go, in the following line:
if (random-float 1 < prob-revision) [update-strategy-after-revision]
And parameter noise is used only in procedure to update-strategy-after-revision, in the following line:
ifelse (random-float 1 < noise)
Whenever NetLogo reads the two lines of code above, it uses the current values of the two parameters. Because of this, we can modify the parameters’ values on the fly and immediately see how that change affects the dynamics of the model.
By contrast, changing the value of parameter n-of-players-for-each-strategy at runtime will have no effect whatsoever. This is so because parameter n-of-players-for-each-strategy is only used in procedure to setup-players, which is executed at the beginning of the simulation –triggered by procedure to setup– and never again.
To enable the user to modify the population size at runtime, we should create a slider for the new parameter n-of-players. Before doing so, we have to remove the declaration of the global variable n-of-players in the Code tab, since the creation of the slider implies the definition of the variable as global.
globals [ payoff-matrix n-of-strategies ;; n-of-players <== we remove this line ]
After creating the slider for parameter n-of-players, we could also remove the monitor showing n-of-players from the interface, since it is no longer needed. Another option (see figure 1 below) is to use that same monitor to display the value of the ticks that have gone by since the beginning of the simulation. To do this, we just have to write the primitive ticks (instead of n-of-players) in the “Reporter” box of the monitor.
The next step is to implement a separate procedure to check whether the value of parameter n-of-players differs from the current number of players in the simulation and, if it does, act accordingly. We find it natural to name this new procedure to update-n-of-players, and one possible implementation would be the following:
to update-n-of-players let diff (n-of-players - count players) if diff != 0 [ ifelse diff > 0 [ repeat diff [ ask one-of players [hatch-players 1] ] ] [ ask n-of (- diff) players [die] ] ] end
Note the use of primitives hatch-players and die to clone and kill agents respectively. The difference between primitives hatch-players and create-players is important. Hatching is an action that only individual agents (i.e. “turtles” and breeds of “turtles”, in NetLogo parlance) can execute. By contrast, only the observer can run create-turtles and create-<breeds> primitives.
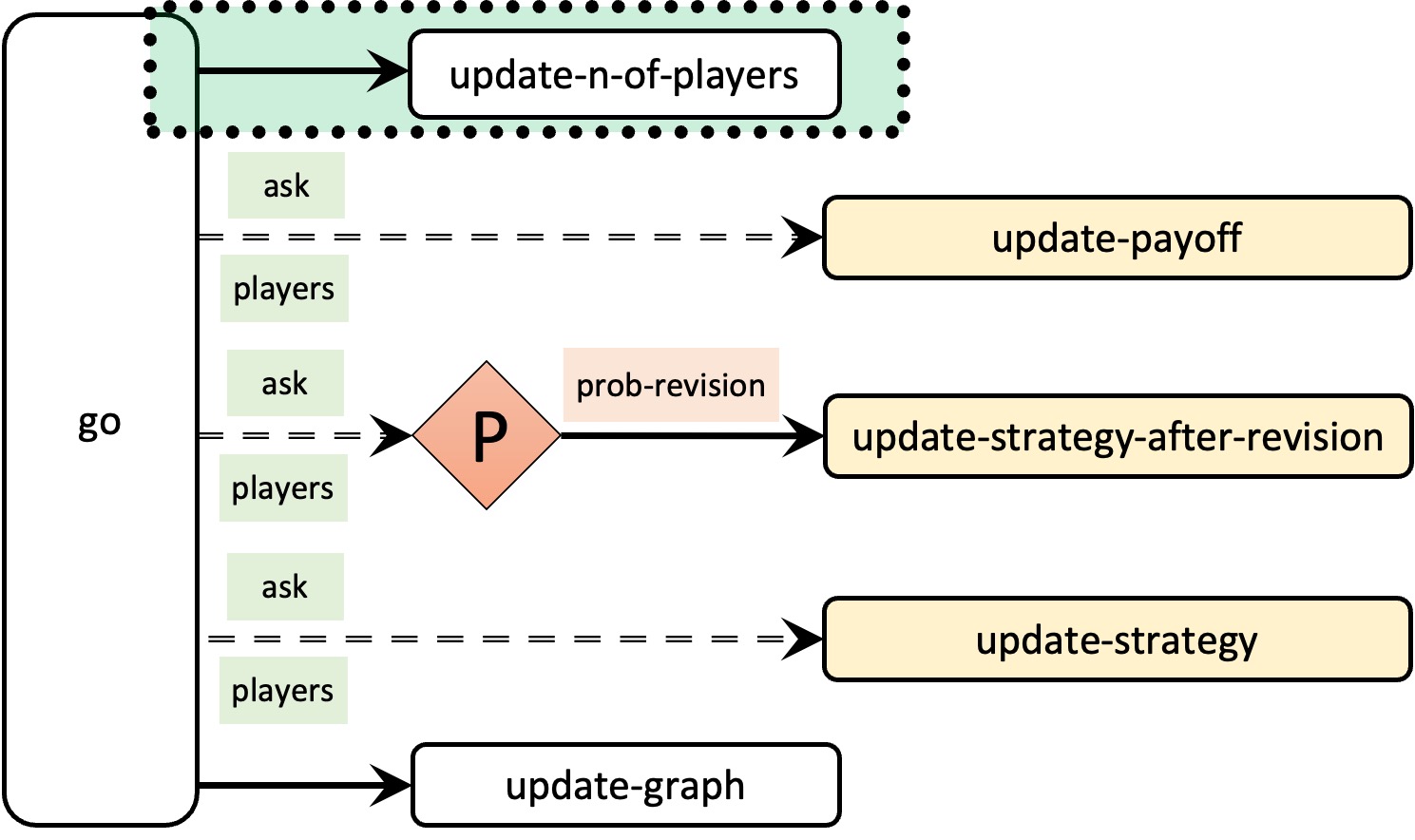
Finally, we should include the call to the new procedure at the beginning of to go.
to go update-n-of-players ;; <== new line ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end
And with this, we’re ready to go! Give it a try, and enjoy the good progress you are making!
Figure 2 below shows the skeleton of our current procedure to go, highlighting the only substantial change we have made so far.
 5. Efficiency
5. Efficiency
Naturally, to make a model run faster, one can always untick the “view updates” box on the Interface tab. The same effect can be achieved by pushing the speed slider –situated in the middle of the interface toolbar– to its rightmost position, or by using primitive no-display in the code. This is a must in models that do not make use of the view, like the ones we are programming here, since it implies a significant speed-up at no cost. Thus, in our model, we should include the primitive no-display in procedure to setup, right after clear-all.
to setup clear-all no-display ;; <== new line setup-payoffs setup-players setup-graph reset-ticks update-graph end
But beyond this simple piece of advice, in general, how can we make our model run faster? In our view, the very first thing we have to do is to find out where our model spends most of the time. The following section shows how to do this.
5.1. Measuring execution speed of different parts of the code
There are two simple ways to measure execution speed in NetLogo. One is using primitives reset-timer and timer. For instance, to time how long it takes to have every agent carry out the operation:
other players
we could write the following reporter:
to-report time-other-players reset-timer ask players [let temporary-var other players] report timer end
The second –more advanced– way of measuring execution speed involves the Profiler Extension, which comes bundled with NetLogo. This extension allows us to see how many times each procedure in our model is called during a run and how long each call takes. The extension is simple to use and it is well documented at its own website. To use it in our model, we should include the extension at the beginning of our code, as follows:
extensions [profiler]
Then we could execute the following procedure, borrowed from the Profiler Extension documentation page. (Please, remember that we have to include the new procedure after the declaration of variables.)
to show-profiler-report setup ;; set up the model profiler:start ;; start profiling repeat 1000 [ go ] ;; run something you want to measure profiler:stop ;; stop profiling print profiler:report ;; print the results profiler:reset ;; clear the data end
Once the procedure is implemented, you can run it by typing its name in the Command Center.
The profiler report includes the inclusive time and the exclusive time for each procedure. Inclusive time is the time the simulation spends running the procedure, i.e. since the procedure is entered until it finishes. Exclusive time is the time passed since the procedure is entered until it finishes, but does not include any time spent in other user-defined procedures which it calls.
Let us see an example of the output printed by show-profiler-report with our current model (nxn-imitate-if-better-noise-interactive-profiler.nlogo). We model Rock-Paper-Scissors game (payoffs = [[0 -1 1][1 0 -1][-1 1 0]]), initial distribution n-of-players-for-each-strategy = [200 200 200], prob-revision = 0.1 and noise = 0.01.
BEGIN PROFILING DUMP Sorted by Exclusive Time Name Calls Incl T(ms) Excl T(ms) Excl/calls UPDATE-PAYOFF 600000 13569.169 13569.169 0.023 UPDATE-STRATEGY 600000 7745.460 7745.460 0.013 UPDATE-STRATEGY-AFT... 60179 796.219 796.219 0.013 GO 1000 22746.879 462.636 0.463 UPDATE-GRAPH 1000 170.606 170.606 0.171 UPDATE-N-OF-PLAYERS 1000 2.788 2.788 0.003 Sorted by Inclusive Time GO 1000 22746.879 462.636 0.463 UPDATE-PAYOFF 600000 13569.169 13569.169 0.023 UPDATE-STRATEGY 600000 7745.460 7745.460 0.013 UPDATE-STRATEGY-AFT... 60179 796.219 796.219 0.013 UPDATE-GRAPH 1000 170.606 170.606 0.171 UPDATE-N-OF-PLAYERS 1000 2.788 2.788 0.003 Sorted by Number of Calls UPDATE-PAYOFF 600000 13569.169 13569.169 0.023 UPDATE-STRATEGY 600000 7745.460 7745.460 0.013 UPDATE-STRATEGY-AFT... 60179 796.219 796.219 0.013 GO 1000 22746.879 462.636 0.463 UPDATE-GRAPH 1000 170.606 170.606 0.171 UPDATE-N-OF-PLAYERS 1000 2.788 2.788 0.003 END PROFILING DUMP
In the example above we can see –among other things– that:
- Simulations spend most of the time executing procedure to update-payoff (13 569 / 22 746 ≈ 60%). This procedure is fairly simple (it only takes 0.023 ms each time it is executed), but the problem is that it is called 600 000 times. This makes sense, since there are 600 agents in this simulation, each of them runs to update-payoff once every tick, and we ran the model for 1000 ticks (600 × 1 × 1000 = 600 000).
- After procedure to update-payoff, simulations spend most of the time running procedure to update-strategy. This procedure is extremely simple, but it is also called 600 000 times. All in all, this procedure takes 7 745 / 22 746 ≈ 34% of simulation time.
- Our implementation to allow the user to modify the number of agents at runtime hardly takes any computing time (just 2.788 ms, i.e., 2.788 / 22 746 ≈ 0.01% of simulation time).
With this information in mind, our next step is to try to identify inefficiencies in our code. These inefficiencies often take one of two possible forms:
- Computations that we conduct but we do not use at all.
- Computations that we conduct several times despite knowing that their outputs will not change.
Let us see an example of each of these inefficiencies in our current code.
5.2. Example of computations that we conduct but do not use
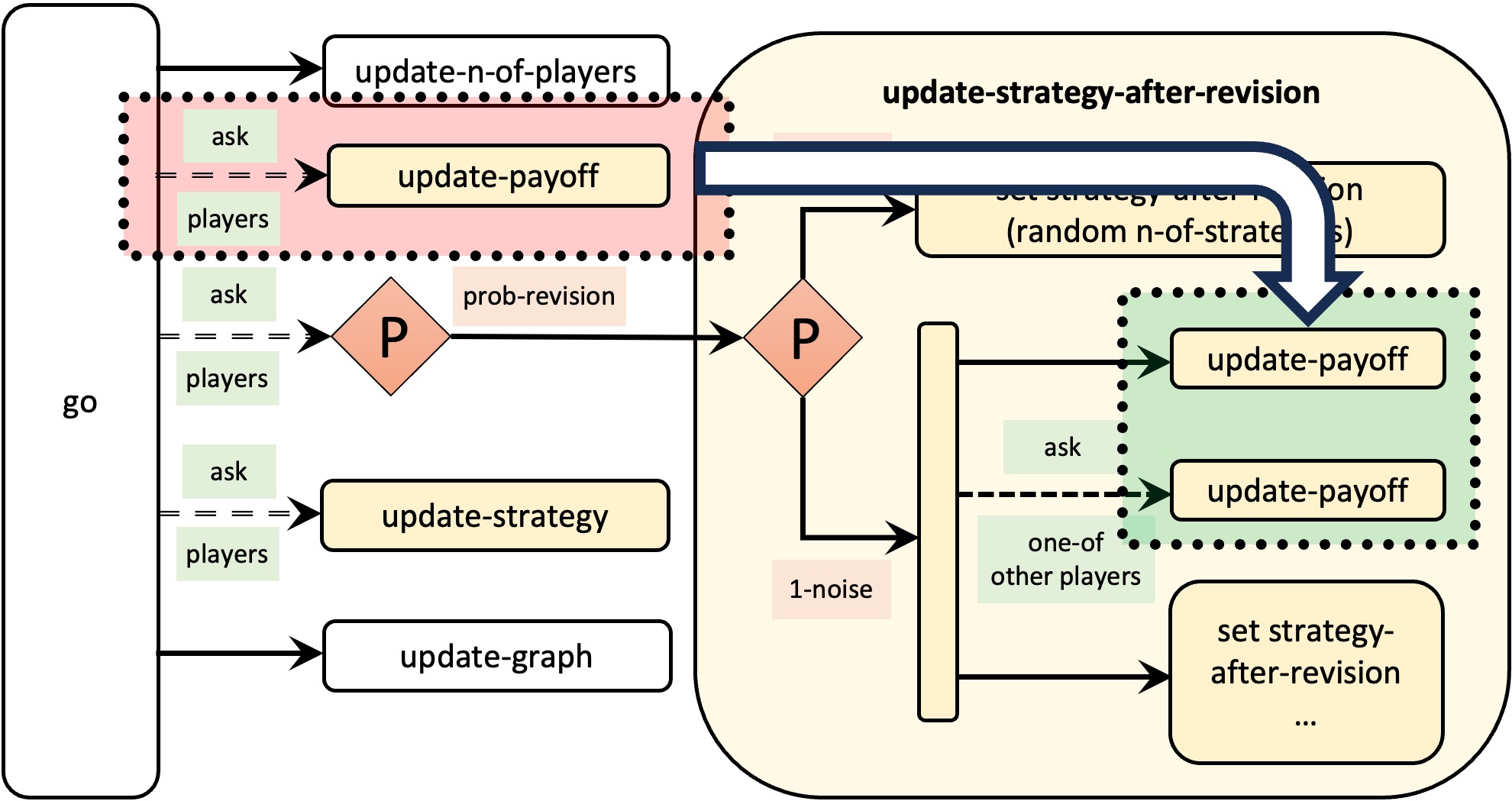
Note that in this model we make all agents update their payoff in every tick, but we only use the payoffs obtained by the revising agents and by the agents they observe. Thus, we can make the model run faster by asking only revising and observed agents to update their payoff. One way of implementing this efficiency improvement would be to modify the code of procedures to go and to update-strategy-after-revision as follows:
to go update-n-of-players ;; ask players [update-payoff] <== We remove this line ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ let observed-player one-of other players update-payoff ;; <== new line ask observed-player [update-payoff] ;; <== new line if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end
These changes, which are summarized in Figure 3 below, will make simulations with low prob-revision run much faster.
In any case, we should double check that we have made our model faster using the profiler extension. The output for the new model (nxn-imitate-if-better-noise-efficient-but-more-than-once-profiler.nlogo) is:
BEGIN PROFILING DUMP Sorted by Exclusive Time Name Calls Incl T(ms) Excl T(ms) Excl/calls UPDATE-STRATEGY 600000 8056.915 8056.915 0.013 UPDATE-PAYOFF 118634 3013.853 3013.853 0.025 UPDATE-STRATEGY-AFT... 59894 4866.334 1852.482 0.031 GO 1000 13623.073 373.725 0.374 UPDATE-GRAPH 1000 320.337 320.337 0.320 UPDATE-N-OF-PLAYERS 1000 5.762 5.762 0.006 Sorted by Inclusive Time GO 1000 13623.073 373.725 0.374 UPDATE-STRATEGY 600000 8056.915 8056.915 0.013 UPDATE-STRATEGY-AFT... 59894 4866.334 1852.482 0.031 UPDATE-PAYOFF 118634 3013.853 3013.853 0.025 UPDATE-GRAPH 1000 320.337 320.337 0.320 UPDATE-N-OF-PLAYERS 1000 5.762 5.762 0.006 Sorted by Number of Calls UPDATE-STRATEGY 600000 8056.915 8056.915 0.013 UPDATE-PAYOFF 118634 3013.853 3013.853 0.025 UPDATE-STRATEGY-AFT... 59894 4866.334 1852.482 0.031 GO 1000 13623.073 373.725 0.374 UPDATE-GRAPH 1000 320.337 320.337 0.320 UPDATE-N-OF-PLAYERS 1000 5.762 5.762 0.006 END PROFILING DUMP
From the report, we can draw the following inferences:
- We have significantly reduced the number of calls to procedure to update-payoff, from 600 000 down to 118 634. This number makes sense, since there were 600 agents in this simulation, prob-revision was 0.1, noise was 0.01, each revision without noise makes two calls to the procedure, and we ran the model 1000 ticks (600 × 0.1 × 0.99 × 2 × 1000 = 118 800). Note, however, that for prob-revision greater than 0.5, the number of calls would be greater with the new implementation. In general, the expected number of calls to procedure to update-payoff in the new model will be (2 × prob-revision × n-of-players × ticks).
- Our change in the code has reduced the simulation time considerably, from 22 746 down to 13 623 ms.
- Now simulations spend most of the time running procedure to update-strategy. This procedure is extremely simple, but it is called 600 000 times. All in all, this procedure takes 8 056 / 13 623 ≈ 59% of simulation time.
The changes we conducted have made our model run much faster (since prob-revision was 0.1 < 0.5). However, note that, by making these changes, we have implemented a slightly different model. In the original implementation, agents would only update their payoff once every tick, but in the new implementation, the same agent could update her payoff several times in the same tick (if, for instance, she is observed several times). This leads to a (very slightly) different distribution of payoffs. Whether this is crucial or not is a matter that would depend on the scientific question we want to answer. In any case, do not worry! We can fix this problem and, at the same time, make our model even more efficient! Let us see how!
Our goal then is to make sure that agents execute procedure to update-payoff at most once in each tick. To make that happen, we have to keep track of whether each individual agent has already executed the procedure in the current tick or not. To that end, we could define a new player-owned variable named played? that will equal true if the agent has already executed procedure to update-payoff in the current tick and false otherwise. We would also have to set the every players’ value of this new variable played? to false at the beginning of the tick. The changes we have to implement in the model to make this work are highlighted below:
players-own [ strategy strategy-after-revision payoff played? ;; <== new line ] to setup-players ;; ... some lines of code ... ;; let i 0 foreach initial-distribution [ j -> create-players j [ set payoff 0 set strategy i set strategy-after-revision strategy set played? false ;; <== new line ] set i (i + 1) ] set n-of-players count players end to go update-n-of-players ask players [set played? false] ;; <== new line ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end to update-payoff let mate one-of other players set payoff item ([strategy] of mate) (item strategy payoff-matrix) set played? true ;; <== new line end to update-strategy-after-revision ifelse (random-float 1 < noise) [ set strategy (random n-of-strategies) ] [ let observed-player one-of other players if not played? [update-payoff] ;; <== modified lines ask observed-player [if not played? [update-payoff]] ;; <== if ([payoff] of observed-player) > payoff [ set strategy ([strategy] of observed-player) ] ] end
The changes implemented above are summarized in Figure 4 below.
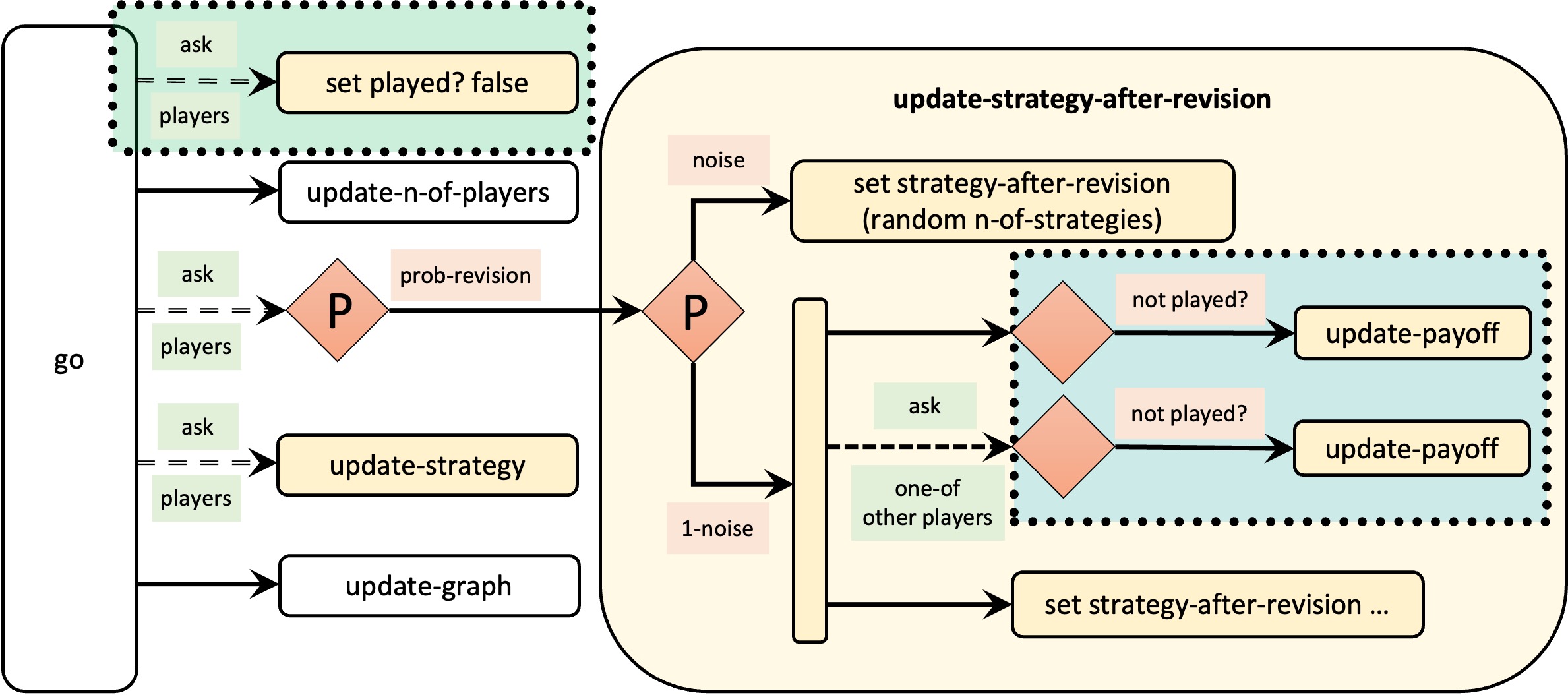
With this new implementation, the expected number of calls to procedure to update-payoff will be less than (2 × prob-revision × n-of-players × ticks) –especially so if prob-revision is high– and never more than (n-of-players × ticks). Thus, the new implementation reduces the number of calls to procedure to update-payoff regardless of the value of prob-revision, and it implements the original model precisely. Thus, one would think that we have made our model even faster but… is that true? Let us check with the profiler extension.
The output for the new model (nxn-imitate-if-better-noise-efficient-played-profiler.nlogo) is:
BEGIN PROFILING DUMP Sorted by Exclusive Time Name Calls Incl T(ms) Excl T(ms) Excl/calls GO 1000 21457.028 8050.356 8.050 UPDATE-STRATEGY 600000 7716.470 7716.470 0.013 UPDATE-PAYOFF 110916 3871.700 3871.700 0.035 UPDATE-STRATEGY-AFT... 60322 5557.386 1685.686 0.028 UPDATE-GRAPH 1000 127.998 127.998 0.128 UPDATE-N-OF-PLAYERS 1000 4.817 4.817 0.005 Sorted by Inclusive Time GO 1000 21457.028 8050.356 8.050 UPDATE-STRATEGY 600000 7716.470 7716.470 0.013 UPDATE-STRATEGY-AFT... 60322 5557.386 1685.686 0.028 UPDATE-PAYOFF 110916 3871.700 3871.700 0.035 UPDATE-GRAPH 1000 127.998 127.998 0.128 UPDATE-N-OF-PLAYERS 1000 4.817 4.817 0.005 Sorted by Number of Calls UPDATE-STRATEGY 600000 7716.470 7716.470 0.013 UPDATE-PAYOFF 110916 3871.700 3871.700 0.035 UPDATE-STRATEGY-AFT... 60322 5557.386 1685.686 0.028 GO 1000 21457.028 8050.356 8.050 UPDATE-GRAPH 1000 127.998 127.998 0.128 UPDATE-N-OF-PLAYERS 1000 4.817 4.817 0.005 END PROFILING DUMP
The following table shows the simulation times and the number of calls to procedure to update-payoff of the different models we have programmed in this chapter up until now, in chronological order:
| Model’s name | Summary | Number of calls to procedure to update-payoff | Simulation time (ms) |
|---|---|---|---|
| nxn-imitate-if-better-noise- interactive-profiler.nlogo | Baseline. All players update their payoff in every tick | 600 000 | 22 746 |
| nxn-imitate-if-better-noise- efficient-but-more-than- once-profiler.nlogo | Only revisers and the players they observe update their payoff. Some players may update their payoff more than once in one tick | 118 634 | 13 623 |
| nxn-imitate-if-better-noise- efficient-played- profiler.nlogo | The number of times that procedure to update-payoff is executed is minimal. Implementation with boolean variable named played? | 110 916 | 21 457 |
Table 1. Simulation times and number of calls to procedure to update-payoff of all the models implemented in this chapter up until now
It may come as a surprise that the last changes we made, which ensure that the model calls procedure to update-payoff as few times as possible, actually make the model much slower, from 13 623 ms up to 21 457 ms! Oh, no! How is that possible? We are calling procedure to update-payoff fewer times! (We went from 118 634 down to 110 916.) Take a look at the profiler report above and try to come up with an answer… This is a tricky one…
Why is the last model so slow?
As you can see in the report, the exclusive time spent in procedure to go each time it is executed has increased a lot: from 0.374 to 8.050 ms. The only change we have made in this procedure has been to include the following line:
ask players [set played? false] ;; <== new line
This line is not as harmless as it seems in current versions of NetLogo, and it is the main responsible for the increase in simulation time.
Our goal now is to implement the same model, but without having to explicitly tell every agent at the beginning of every tick that they have not played yet.
One way we can do this is by using a player-owned variable named tick-I-played-last (instead of boolean variable played?) that will store the tick number at which the player updated her payoff for the last time. Then, we would ask players to update their payoff only if the value of their tick-I-played-last is less than the current tick. The key difference with the previous model is that we do not have to set the value of this new variable tick-I-played-last every tick for every player.
Model nxn-imitate-if-better-noise-efficient-tick-I-played-last-profiler.nlogo implements these changes, which are summarized in Figure 5 below.
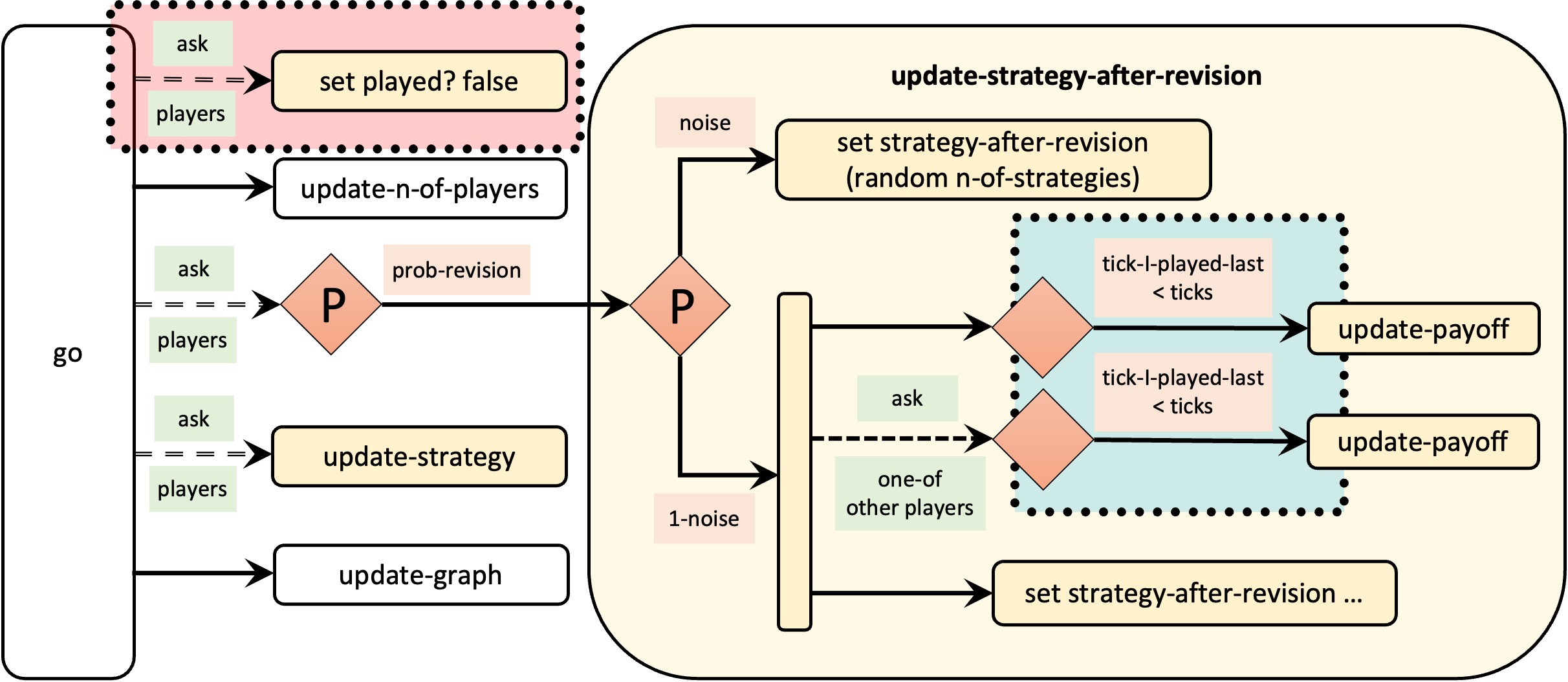
All the necessary changes in the code are highlighted below:
players-own [ strategy strategy-after-revision payoff ;; played? <== deleted line tick-I-played-last ;; <== new line ] to setup-players ;; ... some lines of code ... ;; let i 0 foreach initial-distribution [ j -> create-players j [ set payoff 0 set strategy i set strategy-after-revision strategy ;; set played? false <== deleted line set tick-I-played-last -1 ;; <== new line ] set i (i + 1) ] set n-of-players count players end to go update-n-of-players ;; ask players [set played? false] <== deleted line ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end to update-payoff let mate one-of other players set payoff item ([strategy] of mate) (item strategy payoff-matrix) ;; set played? true <== deleted line set tick-I-played-last ticks ;; <== new line end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ let observed-player one-of other players ;; vvv modified lines below vvv if (tick-I-played-last < ticks) [update-payoff] ask observed-player [ if (tick-I-played-last < ticks) [update-payoff] ] if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end
The output of profiler for the new model (nxn-imitate-if-better-noise-efficient-tick-I-played-last-profiler.nlogo) is:
BEGIN PROFILING DUMP Sorted by Exclusive Time Name Calls Incl T(ms) Excl T(ms) Excl/calls UPDATE-STRATEGY 600000 7462.968 7462.968 0.012 UPDATE-PAYOFF 110211 3927.434 3927.434 0.036 UPDATE-STRATEGY-AFT... 59846 5527.475 1600.041 0.027 GO 1000 13416.363 279.186 0.279 UPDATE-GRAPH 1000 144.769 144.769 0.145 UPDATE-N-OF-PLAYERS 1000 1.964 1.964 0.002 Sorted by Inclusive Time GO 1000 13416.363 279.186 0.279 UPDATE-STRATEGY 600000 7462.968 7462.968 0.012 UPDATE-STRATEGY-AFT... 59846 5527.475 1600.041 0.027 UPDATE-PAYOFF 110211 3927.434 3927.434 0.036 UPDATE-GRAPH 1000 144.769 144.769 0.145 UPDATE-N-OF-PLAYERS 1000 1.964 1.964 0.002 Sorted by Number of Calls UPDATE-STRATEGY 600000 7462.968 7462.968 0.012 UPDATE-PAYOFF 110211 3927.434 3927.434 0.036 UPDATE-STRATEGY-AFT... 59846 5527.475 1600.041 0.027 GO 1000 13416.363 279.186 0.279 UPDATE-GRAPH 1000 144.769 144.769 0.145 UPDATE-N-OF-PLAYERS 1000 1.964 1.964 0.002 END PROFILING DUMP
It is then corroborated that this last version is the most efficient (comparable to the second one if prob-revision is low) and it implements the original model exactly. The table below shows the simulation times and the number of calls to procedure to update-payoff of all the models implemented in this chapter up until now:
| Model’s name | Summary | Number of calls to procedure to update-payoff | Simulation time (ms) |
|---|---|---|---|
| nxn-imitate-if-better-noise- interactive-profiler.nlogo | Baseline. All players update their payoff in every tick | 600 000 | 22 746 |
| nxn-imitate-if-better-noise- efficient-but-more-than- once-profiler.nlogo | Only revisers and the players they observe update their payoff. Some players may update their payoff more than once in one tick | 118 634 | 13 623 |
| nxn-imitate-if-better-noise- efficient-played- profiler.nlogo | The number of times that procedure to update-payoff is executed is minimal. Implementation with boolean variable named played? | 110 916 | 21 457 |
| nxn-imitate-if-better-noise- efficient-tick-I-played-last- profiler.nlogo | The number of times that procedure to update-payoff is executed is minimal. Implementation with variable named tick-I-played-last | 110 211 | 13 416 |
Table 2. Simulation times and number of calls to procedure to update-payoff of all the models implemented in this chapter up until now
Finally, note that, looking at the output printed by show-profiler-report, it still seems wasteful to make all agents update their strategies, even when they do not revise them. In exercise 5 below, we ask you to think about how you would make only revising agents call procedure to update-strategy.
5.3. Example of computations that we conduct several times when once would do
Let us now focus on the second type of inefficiency pointed out above. Can you identify any computations that we repeatedly conduct in every tick, even though its result does not change?
Note that we undertake the computation:
other players
several times in every tick, but we could conduct it just once for each agent in each simulation. To be sure, we conduct that operation every time an agent computes her payoff in to update-payoff:
let mate one-of other players
And also every time an agent revises her strategy in to update-strategy-after-revision:
let observed-agent one-of other players
This computation may not sound very expensive, but if the number of agents is large, it may well be (see exercise 3 below). To make the model run faster, we could create an individually-owned variable named e.g. other-players, as follows
players-own [ strategy strategy-after-revision payoff tick-I-played-last other-players ]
And then we should set the new individually-owned variable other-players to the appropriate value only once at the beginning of each simulation (at the end of procedure to setup-players).
ask players [ set other-players other players ]
Since we may change the number of players at runtime, we should also include the line above in the block of code where we clone or kill agents in procedure to update-n-of-players, i.e.
to update-n-of-players let diff (n-of-players - count players) if diff != 0 [ ifelse diff > 0 [ repeat diff [ ask one-of players [hatch-players 1] ] ] [ ask n-of (- diff) players [die] ] ask players [set other-players other players] ] end
Once we have done that, in the two lines of code where we had the reporter
other players
we should write other-players instead. These changes will make simulations with many players run faster. To find out how much faster, we should use the profiler extension again. The report of profiler for the new model (nxn-imitate-if-better-noise-efficient-tick-I-played-last-and-other-players-profiler.nlogo) is:
BEGIN PROFILING DUMP Sorted by Exclusive Time Name Calls Incl T(ms) Excl T(ms) Excl/calls UPDATE-STRATEGY 600000 7923.625 7923.625 0.013 UPDATE-PAYOFF 110079 3063.731 3063.731 0.028 UPDATE-STRATEGY-AFT... 59798 4255.300 1191.569 0.020 GO 1000 12607.398 283.696 0.284 UPDATE-GRAPH 1000 141.295 141.295 0.141 UPDATE-N-OF-PLAYERS 1000 3.482 3.482 0.003 Sorted by Inclusive Time GO 1000 12607.398 283.696 0.284 UPDATE-STRATEGY 600000 7923.625 7923.625 0.013 UPDATE-STRATEGY-AFT... 59798 4255.300 1191.569 0.020 UPDATE-PAYOFF 110079 3063.731 3063.731 0.028 UPDATE-GRAPH 1000 141.295 141.295 0.141 UPDATE-N-OF-PLAYERS 1000 3.482 3.482 0.003 Sorted by Number of Calls UPDATE-STRATEGY 600000 7923.625 7923.625 0.013 UPDATE-PAYOFF 110079 3063.731 3063.731 0.028 UPDATE-STRATEGY-AFT... 59798 4255.300 1191.569 0.020 GO 1000 12607.398 283.696 0.284 UPDATE-GRAPH 1000 141.295 141.295 0.141 UPDATE-N-OF-PLAYERS 1000 3.482 3.482 0.003 END PROFILING DUMP
We can see that the execution time of procedures to update-payoff and to update-strategy-after-revision has been reduced, as expected, but the overall simulation time has not decreased substantially. The table below summarizes the simulation times and the number of calls to procedure to update-payoff of all the models implemented in this chapter:
| Model’s name | Summary | Number of calls to procedure to update-payoff | Simulation time (ms) |
|---|---|---|---|
| nxn-imitate-if-better-noise- interactive-profiler.nlogo | Baseline. All players update their payoff in every tick | 600 000 | 22 746 |
| nxn-imitate-if-better-noise- efficient-but-more-than- once-profiler.nlogo | Only revisers and the players they observe update their payoff. Some players may update their payoff more than once in one tick | 118 634 | 13 623 |
| nxn-imitate-if-better-noise- efficient-played- profiler.nlogo | The number of times that procedure to update-payoff is executed is minimal. Implementation with boolean variable named played? | 110 916 | 21 457 |
| nxn-imitate-if-better-noise- efficient-tick-I-played-last- profiler.nlogo | The number of times that procedure to update-payoff is executed is minimal. Implementation with variable named tick-I-played-last | 110 211 | 13 416 |
| nxn-imitate-if-better-noise- efficient-tick-I-played-last- and-other-players- profiler.nlogo | We also use variable other-players | 110 079 | 12 607 |
Table 3. Simulation times and number of calls to procedure to update-payoff of all the models implemented in this chapter
5.4. Other tips to improve the efficiency of NetLogo code
Railsback et al. (2017) give several guidelines to identify slow parts of NetLogo code and make them run faster, providing specific examples for agent-based models written in NetLogo.
5.5. Take-home message
The main lesson we would like you to take home from this chapter is methodological: if you want to make a model run faster, you should definitely use the profiler extension, i.e. start by looking at the data. This is because NetLogo, like any other programming language, has been optimized to compute things in a certain way, and this way may be different from other programming languages you may be familiar with, and may even change from one version of NetLogo to the next. Thus, our most important piece of advice is: look at the evidence by using the profiler extension and try different ways of coding. By doing so, you will develop skills that will help you implement your models more efficiently.
 6. Complete code in the Code tab
6. Complete code in the Code tab
extensions [profiler] globals [ payoff-matrix n-of-strategies ] breed [players player] players-own [ strategy strategy-after-revision payoff tick-I-played-last other-players ] to show-profiler-report setup ;; set up the model profiler:start ;; start profiling repeat 1000 [ go ] ;; run something you want to measure profiler:stop ;; stop profiling print profiler:report ;; print the results profiler:reset ;; clear the data end to setup clear-all no-display setup-payoffs setup-players setup-graph reset-ticks update-graph end to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix end to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] let i 0 foreach initial-distribution [ j -> create-players j [ set payoff 0 set strategy i set strategy-after-revision strategy set tick-I-played-last -1 ] set i (i + 1) ] set n-of-players count players ask players [ set other-players other players ] end to setup-graph set-current-plot "Strategy Distribution" foreach (range n-of-strategies) [ i -> create-temporary-plot-pen (word i) set-plot-pen-mode 1 set-plot-pen-color 25 + 40 * i ] end to go update-n-of-players ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end to update-payoff let mate one-of other-players set payoff item ([strategy] of mate) (item strategy payoff-matrix) set tick-I-played-last ticks end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ let observed-player one-of other-players if (tick-I-played-last < ticks) [update-payoff] ask observed-player [ if (tick-I-played-last < ticks) [update-payoff] ] if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end to update-strategy set strategy strategy-after-revision end to update-graph let strategy-numbers (range n-of-strategies) let strategy-frequencies map [ n -> count players with [strategy = n] / n-of-players ] strategy-numbers set-current-plot "Strategy Distribution" let bar 1 foreach strategy-numbers [ n -> set-current-plot-pen (word n) plotxy ticks bar set bar (bar - (item n strategy-frequencies)) ] set-plot-y-range 0 1 end to update-n-of-players let diff (n-of-players - count players) if diff != 0 [ ifelse diff > 0 [ repeat diff [ ask one-of players [hatch-players 1] ] ] [ ask n-of (- diff) players [die] ] ask players [ set other-players other players ] ] end
7. Sample run
Now that we can change the population size at runtime, we can easily explore the question posed above: How does population size affect the dynamics of the imitate-if-better decision rule with noise in the Rock-Paper-Scissors game? To do that, let us use the same setting as in the previous chapters (i.e. payoffs = [[0 -1 1][1 0 -1][-1 1 0]] and prob-revision = 0.1), start with a small population of 60 agents (n-of-players-for-each-strategy = [20 20 20]), and then, increase n-of-players up to 2000 at runtime. The following video shows a representative run with these settings, where we increased the population size from 60 to 2000 at tick 4000.
As you can see, when the number of agents is small, the population consistently follows cycles of large amplitude among the three strategies. The cycles are so wide that sometimes one or even two strategies go extinct for a while. In stark contrast, when the population is large, the cycles get much smaller and the population tends to linger around the state where each strategy is used by approximately a third of the population.[1]
8. Exercises
You can use the following link to download the last NetLogo model we implemented in this chapter: nxn-imitate-if-better-noise-efficient-tick-I-played-last-and-other-players-profiler.nlogo.

![]() Exercise 1. In this chapter we have improved both the interactivity and the efficiency of our model. Can you quantify how much faster the last version of our code runs compared to the previous one (nxn-imitate-if-better-noise)? For the sake of concreteness, use 1000-tick simulations with payoffs = [[0 -1 1][1 0 -1][-1 1 0]], initial distribution n-of-players-for-each-strategy = [300 300 300], prob-revision = 0.1 and noise = 0.01.
Exercise 1. In this chapter we have improved both the interactivity and the efficiency of our model. Can you quantify how much faster the last version of our code runs compared to the previous one (nxn-imitate-if-better-noise)? For the sake of concreteness, use 1000-tick simulations with payoffs = [[0 -1 1][1 0 -1][-1 1 0]], initial distribution n-of-players-for-each-strategy = [300 300 300], prob-revision = 0.1 and noise = 0.01.
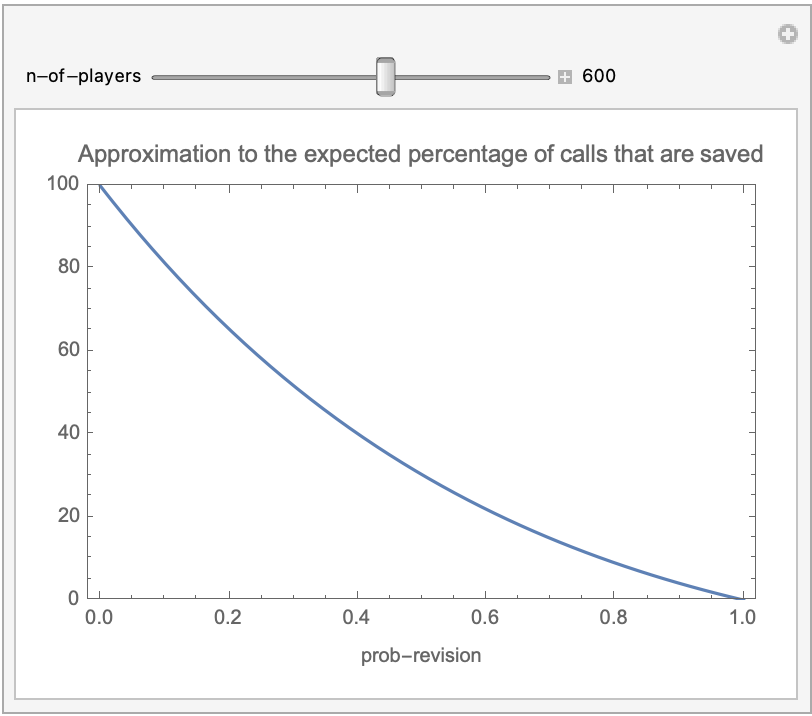
Exercise 2. In this chapter we have drastically reduced the number of times that procedure to update-payoff is called. Can you derive an analytical approximation to the percentage of calls to this procedure that the new implementation is expected to save, as a function of prob-revision and n-of-players? (You may consider noise = 0 initially).
Plot of an approximation to the expected percentage of calls to procedure to update-payoff that are saved
The plot below shows an approximation to the expected percentage of calls to procedure to update-payoff that the last three NetLogo models implemented in this chapter save (i.e., the efficient models that guarantee that players execute this procedure at most once in each tick), as a function of prob-revision, for different values of the number of players n-of-players. It is interesting to see that this function is not very sensitive to the number of players n-of-players. It is assumed that noise = 0.
![]() Exercise 3. In this chapter we have reduced the number of times the computation
Exercise 3. In this chapter we have reduced the number of times the computation other players is conducted by creating an individually-owned variable (named other-players). To compare these two approaches, write a short NetLogo program where 10000 agents conduct this operation.
![]() Exercise 4. What changes would you have to make in the code so revising agents within the tick update their strategies sequentially (in random order), rather than simultaneously?
Exercise 4. What changes would you have to make in the code so revising agents within the tick update their strategies sequentially (in random order), rather than simultaneously?
Hint to implement asynchronous strategy updating
It is possible to do this by making a minor change in procedure to go, without touching the rest of the code.
![]() Exercise 5. What changes would you have to make in the code so it is only revising agents that call procedure to update-strategy? Use the profiler extension to find out whether the new model is faster. To facilitate the comparison, use the same parameter settings as in Table 3.
Exercise 5. What changes would you have to make in the code so it is only revising agents that call procedure to update-strategy? Use the profiler extension to find out whether the new model is faster. To facilitate the comparison, use the same parameter settings as in Table 3.
Hint to implement a version where only revising agents call procedure to update-strategy
let revising-players players with [random-float 1 < prob-revision]
- The state where all strategies are equally represented is a globally asymptotically stable state of the mean dynamics of this model (which provides a good approximation for models with large populations). See solution to Exercise 2.3.2. ↵