Part II. Our first agent-based evolutionary model
II-1. Our very first model
1. Goal
The goal of this chapter is to create our first agent-based evolutionary model in NetLogo. Being our first model, we will keep it simple; nonetheless, the model will already contain the four building blocks that define most models in agent-based evolutionary game theory, namely:
- a population of agents,
- a game that is recurrently played by the agents,
- a procedure that determines how strategy revision opportunities are assigned to agents, and
- a decision rule, which specifies how individual agents update their (pure) strategies when they are given the opportunity to revise.
In particular, in our model the number of (individually-represented) agents in the population will be chosen by the user. These agents will repeatedly play a symmetric 2-player 2-strategy game, each time with a randomly chosen counterpart. The payoffs of the game will be determined by the user. Agents will revise their strategy with a certain probability, also to be chosen by the user. The decision rule these agents will use is called imitate-if-better, which dictates that a revising agent imitates the strategy of a randomly chosen player, if this player obtained a payoff greater than the revising agent’s.
This fairly general model will allow us to explore a variety of specific questions, like the one we outline next.
2. Motivation. Cooperation in social dilemmas
There are many situations in life where we have the option to make a personal effort that will benefit others beyond the personal cost incurred. This type of behavior is often termed “to cooperate”, and can take a myriad forms: from paying your taxes, to inviting your friends over for a home-made dinner. All these situations, where cooperating involves a personal cost but creates net social value, exhibit the somewhat paradoxical feature that individuals would prefer not to pay the cost of cooperation, but everyone prefers the situation where everybody cooperates to the situation where no one does. Such counterintuitive characteristic is the defining feature of social dilemmas, and life is full of them (Dawes, 1980).
The essence of many social dilemmas can be captured by a simple 2-person game called the Prisoner’s Dilemma. In this game, the payoffs for the players are: if both cooperate, R (Reward); if both defect, P (Punishment); if one cooperates and the other defects, the cooperator obtains S (Sucker) and the defector obtains T (Temptation). The payoffs satisfy the condition T > R > P > S. Thus, in a Prisoner’s Dilemma, both players prefer mutual cooperation to mutual defection (R > P), but two motivations may drive players to behave uncooperatively: the temptation to exploit (T > R), and the fear to be exploited (P > S).
Let us see a concrete example of a Prisoner’s Dilemma. Imagine that you have $1000, which you may keep for yourself, or transfer to another person’s account. This other person faces the same decision: she can transfer her $1000 money to you, or else keep it. Crucially, whenever money is transferred, the money doubles, i.e. the recipient gets $2000.
Try to formalize this situation as a game, assuming you and the other person only care about money.
The game can be summarized using the payoff matrix in Fig. 1. To see that this game is indeed a Prisoner’s Dilemma, note that transferring the money would be what is often called “to cooperate”, and keeping the money would be “to defect”.
| Player 2 | |||
| Keep | Transfer | ||
| Player 1 | Keep | 1000 , 1000 | 3000 , 0 |
| Transfer | 0 , 3000 | 2000 , 2000 | |
Figure 1. Payoff matrix of a Prisoner’s Dilemma game
To explore whether cooperation may be sustained in a simple evolutionary context, we can model a population of agents who repeatedly play the Prisoner’s Dilemma. Agents are either cooperators or defectors, but they can occasionally revise their strategy. A revising agent looks at another agent in the population and, if the observed agent’s payoff is greater than the revising agent’s payoff, the revising agent copies the observed agent’s strategy. Do you think that cooperation will be sustained in this setting? Here we are going to build a model that will allow us to investigate this question… and many others!
3. Description of the model
In this model, there is a population of n-of-players agents who repeatedly play a symmetric 2-player 2-strategy game. The two possible strategies are labeled 0 and 1. The payoffs of the game are determined by the user in the form of a matrix [[A00 A01] [A10 A11]], where Aij is the payoff that an agent playing strategy i obtains when meeting an agent playing strategy j (i, j ∈ {0, 1}).
Initially, the number of agents playing strategy 1 is a (uniformly distributed) random number between 0 and the number of players in the population. From then onwards, the following sequence of events –which defines a tick– is repeatedly executed:
- Every agent obtains a payoff by selecting another agent at random and playing the game.
- With probability prob-revision, individual agents are given the opportunity to revise their strategies. The decision rule –called imitate if better– reads as follows:[1]
Look at another (randomly selected) agent and adopt her strategy if and only if her payoff was greater than yours.
The model shows the evolution of the number of agents choosing each of the two possible strategies at the end of every tick.
 4. Interface design
4. Interface design
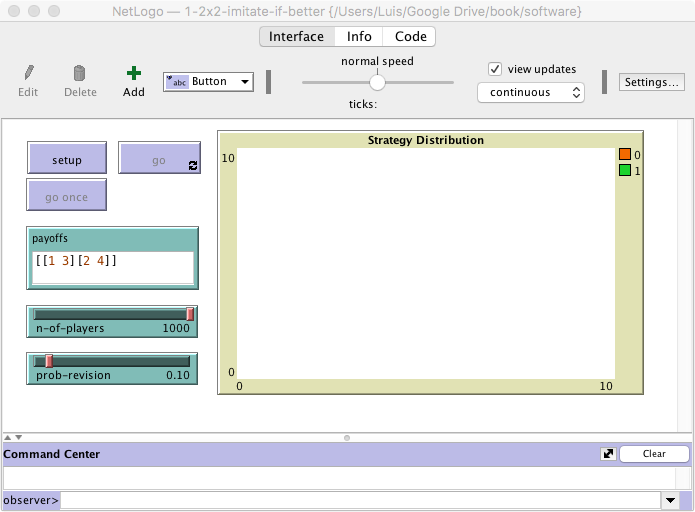
The interface (see figure 2) includes:
- Three buttons:
- One button named , which runs the procedure to setup.
- One button named , which runs the procedure to go.
- One button named , which runs the procedure to go indefinitely.
In the Code tab, write the procedures to setup and to go, without including any code inside for now.to setup ;; empty for now end to go ;; empty for now end
In the Interface tab, create a button and write setup in the “commands” box. This will make the procedure to setup run whenever the button is pressed.
Create another button for the procedure to go (i.e., write go in the commands box) with display name to emphasize that pressing the button will run the procedure to go just once.
Finally, create another button for the procedure to go, but this time tick the “forever” option. When pressed, this button will make the procedure to go run repeatedly until the button is pressed again.
- A slider to let the user select the number of players.
Create a slider for global variable n-of-players. You can choose limit values 2 (as the minimum) and 1000 (as the maximum), and an increment of 1.
- An input box where the user can write a string of the form [ [A00 A01] [A10 A11] ] containing the payoffs Aij that an agent playing strategy i obtains when meeting an agent playing strategy j (i, j ∈ {0, 1}).
Create an input box with associated global variable payoffs. Set the input box type to “String (reporter)”. Note that the content of payoffs will be a string (i.e. a sequence of characters) from which we will need to extract the payoff numeric values.
- A slider to let the user select the probability of revision.
Create a slider with associated global variable prob-revision. Choose limit values 0 and 1, and an increment of 0.01.
- A plot that will show the evolution of the number of agents playing each strategy.
Create a plot and name it Strategy Distribution. Since we are not going to use the 2D view (i.e. the large black square in the interface) in this model, you may want to overlay it with the newly created plot.
 5. Code
5. Code
5.1. Initial skeleton of the code
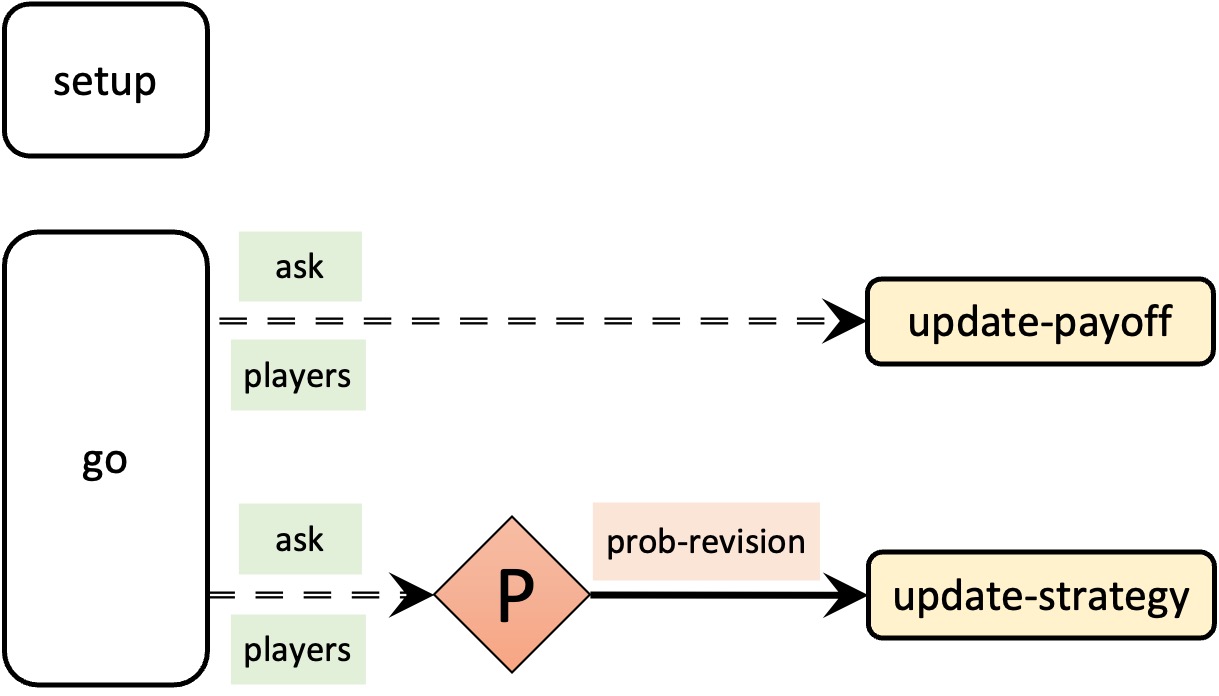
Figure 3 below provides a schematic view of the code. We will use these code skeletons in many chapters of this book. You can find the legend for them in Appendix A-2.
5.2. Global variables and individually-owned variables
First we declare the global variables that we are going to use and we have not already declared in the interface. We will be using a global variable named payoff-matrix to store the payoff values on a list, so the first line of code in the Code tab will be:
globals [payoff-matrix]
Next we declare a breed of agents called “players”. If we did not do this, we would have to use the default name “turtles”, which may be confusing to newcomers.
breed [players player]
Individual players have their own strategy (which can be different from the other agents’ strategy) and their own payoff, so we need to declare these individually-owned variables as follows:
players-own [ strategy payoff ]
5.3. Setup procedures
In the setup procedure we want:
- To clear everything up. We initialize the model afresh using the primitive clear-all:
clear-all - To transform the string of characters the user has written in the payoffs input box (e.g. “[[1 2][3 4]]”) into a list (of 2 lists) that we can use in the code (e.g. [[1 2][3 4]]). This list of lists will be stored in the global variable named payoff-matrix. To do this transformation (from string to list, in this case), we can use the primitive read-from-string as follows:
set payoff-matrix read-from-string payoffs
- To create n-of-players players and set their individually-owned variables to an appropriate initial value. At first, we set the value of payoff and strategy to 0:[2]
create-players n-of-players [ set payoff 0 set strategy 0 ]
Note that the primitive create-players does not appear in the NetLogo dictionary; it has been automatically created after defining the breed “players”. Had we not defined the breed “players”, we would have had to use the primitive create-turtles instead.
Now we will ask a random number of players (between 0 and n-of-players) to set their strategy to 1, using one of the most important primitives in NetLogo, namely ask. The instruction will be of the form:
ask AGENTSET [set strategy 1]
where
AGENTSETshould be a random subset of players.To randomly select a certain number of agents from an agentset (such as players), we can use the primitive n-of (which reports another –usually smaller– agentset):
ask (n-of SIZE players) [set strategy 1]
where
SIZEis the number of players we would like to select.Finally, to generate a random integer between 0 and n-of-players we can use the primitive random:
random (n-of-players + 1)
The resulting instruction will be:
ask n-of (random (n-of-players + 1)) players [set strategy 1]
- To initialize the tick counter. At the end of the setup procedure, we should include the primitive reset-ticks, which resets the tick counter to zero (and also runs the “plot setup commands”, the “plot update commands” and the “pen update commands” in every plot, so the initial state of the model is plotted):
reset-ticks
Thus, the code up to this point should be as follows:
globals [ payoff-matrix ] breed [players player] players-own [ strategy payoff ] to setup clear-all set payoff-matrix read-from-string payoffs create-players n-of-players [ set payoff 0 set strategy 0 ] ask n-of random (n-of-players + 1) players [set strategy 1] reset-ticks end to go end
5.4. Go procedure
The procedure to go contains all the instructions that will be executed in every tick. In this particular model, these instructions include
- asking all players to interact with another (randomly selected) player to obtain a payoff, and
- asking all players to revise their strategy with probability prob-revision.
To keep things nice and modular, we will create two separate procedures to be run by players named to update-payoff and to update-strategy. Procedure to update-payoff will update the payoff of the player running the procedure, while procedure to update-strategy will be in charge of updating her strategy. Writing short procedures with meaningful names will make our code elegant, easy to understand, easy to debug, and easy to extend… so we should definitely aim for that.
We now have to think very carefully about the order in which we are going to ask the players to update-payoff and to update-strategy. Should players update their strategies at the same time (i.e. synchronously), or sequentially (i.e. asynchronously)? Arguably, this is something that is not absolutely clear in the description of the model above. We chose to describe the model in that (admittedly ambiguous) way because it is common that the relative order in which agents run their actions is not absolutely clear in model descriptions. However, this is a very important issue with significant consequences, and it already takes some expertise even to only notice that a model description is ambiguous. The following sections will help us develop this expertise.
A naive implementation
Let us start with the implementation that seems to follow the model description most closely, and which corresponds with the initial skeleton of the code shown in figure 3. First, all agents update their payoff; then, all agents update their strategies with probability prob-revision. Procedure to go would then look as follows:
ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [update-strategy] ]
Note that condition
(random-float 1 < prob-revision)
will be true with probability prob-revision.
The implementation of procedure to go shown above seems natural and straightforward. However, it is faulty in a subtle but crucial way. The implementation above would do something that –most likely– the designer of the model did not intend.
To see this, think of the first agent who revises her strategy and changes it (in procedure to update-strategy). This agent would have her strategy changed, but her payoff would not change after the revision (because payoffs are only modified in procedure to update-payoff). Thus, her payoff would still correspond to a game played with her old strategy, i.e., her strategy before the revision took place. If, after this first revision, a second agent runs procedure to update-strategy and –having looked at the first agent’s payoff– decides to imitate the first agent, this second agent will imitate the first agent’s new strategy, which is a strategy that was not used to obtain the payoff on which the imitation is based.
Thus, with this first (and naive) implementation, some strategies may be imitated based on payoffs that have not been obtained with those strategies. In the following section we propose an implementation that solves this issue.
A more functional implementation. Synchronous updating within the tick
In this section we propose an implementation of procedure to go that:
- guarantees that any imitation of a strategy is based on the payoff obtained with that strategy, and
- in our opinion, corresponds best with the description of the model above. Arguably, the description above seems to imply that revising agents within the tick update their strategies simultaneously.
To make sure that revising players within the tick update their strategies simultaneously, we need players to be able to compute their revised strategy, but they also must be able to keep their old one until all players have had the opportunity to revise their strategy. Therefore, we are going to need two individually-owned variables: one named strategy (for the strategy used to compute the payoffs), and another one named strategy-after-revision (for the strategy that agents will adopt after their revision). Thus, we are going to have to add the following line:
players-own [ strategy strategy-after-revision ;; <== new line payoff ]
Similarly, we will also need two different procedures to be run by individual players: one named to update-strategy-after-revision (where agents will update their strategy-after-revision), and another one named to update-strategy (where agents will update their strategy, with the value of their strategy-after-revision). Procedure to update-strategy should be executed only after all agents have finished revising, to make sure that any imitation of any strategy is based on the payoff obtained with that strategy.
This is a major (and necessary) change to the skeleton of the code. The new skeleton of the code is shown in figure 4, which we recommend comparing with the initial (and faulty) skeleton shown in figure 3.
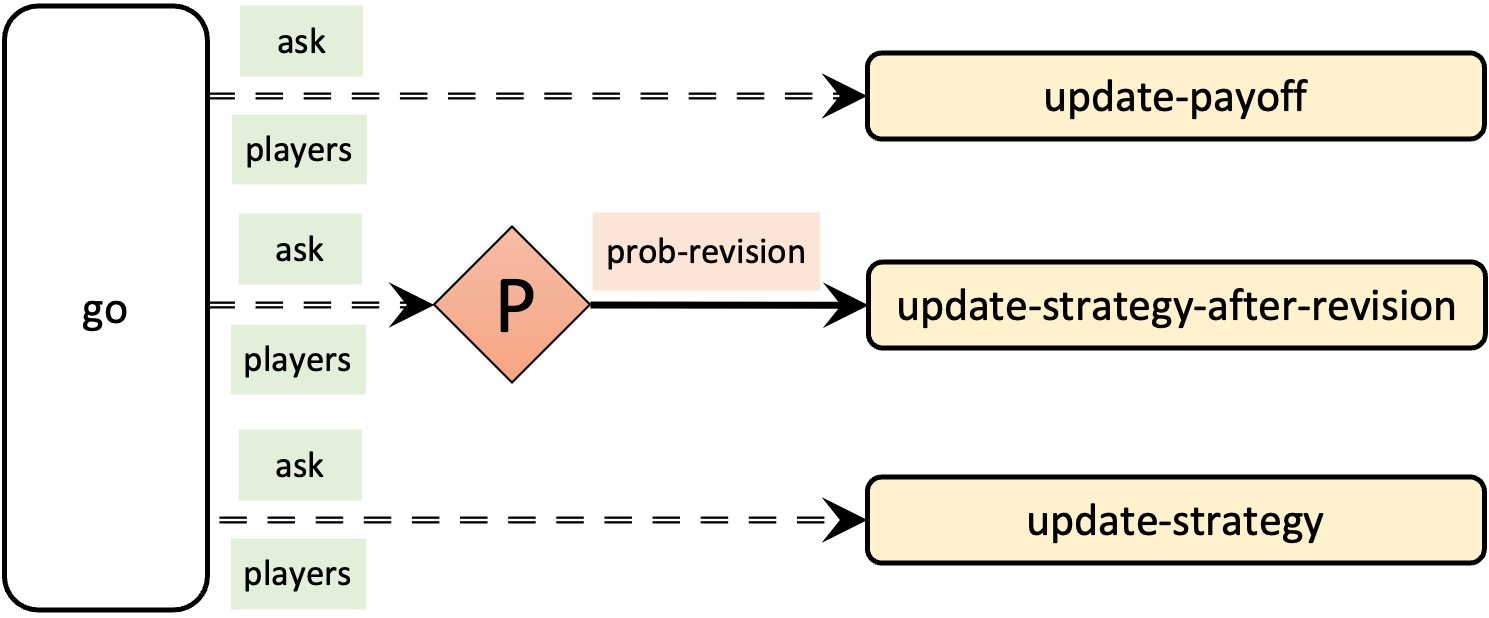
In terms of code, the implementation of procedure to go for synchronous updating within the tick would be as follows:
ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy]
Note that the last line of code above (where players update their strategy with the value of their strategy-after-revision and do nothing else in between) effectively implies that we update every agent’s strategy at the same time within the tick, i.e., revisions are synchronous within the tick. Thus, with this implementation, the value of prob-revision allows us to control the fraction of agents who revise their strategies simultaneously, i.e. under exactly the same information.
Finally, having the agents go once through the code above will mark an evolution step (or generation), so, to keep track of these cycles and have the plots in the interface automatically updated at the end of each cycle, we include the primitive tick at the end of to go.
tick
5.5 Other procedures
to update-payoff
Procedure to update-payoff is the procedure where agents update their payoff. Importantly, note that procedure to update-payoff will be run by a particular player. Thus, within the code of this procedure, we can access and set the value of player-owned variables strategy and payoff.
Here we want the player running this procedure (let us call her the running player) to play with some other player and get the corresponding payoff.[3] First, we will (randomly) select a counterpart and store it in a local variable named mate:
let mate one-of other players
Now we need to compute the payoff that the running player will obtain when she plays the game with her mate. This payoff is an element of the payoff-matrix list, which is made up of two sublists (e.g., [[1 2][3 4]]).
Note that the first sublist (i.e., item 0 payoff-matrix) corresponds to the case in which the running player plays strategy 0. We want to consider the sublist corresponding to the player’s strategy, so we type:
item strategy payoff-matrix
In a similar fashion, the payoff to extract from this sublist is determined by the strategy of the running player’s mate (i.e., [strategy] of mate). Thus, the payoff obtained by the running agent is:
item ([strategy] of mate) (item strategy payoff-matrix)
Finally, to make the running agent store her payoff, we can write:
set payoff item ([strategy] of mate) (item strategy payoff-matrix)
This line of code concludes the definition of the procedure to update-payoff.
to update-strategy-after-revision
In this procedure, which is also to be run by individual players, we want the running player to look at some other random player (which we will call the observed-agent) and, if the payoff of the observed-agent is greater than her own payoff, set the value of her variable strategy-after-revision to the observed-agent’s strategy. We do not want the revising agent to set the value of her variable strategy yet because, as explained above, this would imply that some imitations could then be based on the wrong payoffs.
To select a random player and store it in the local variable observed-agent, we can write:
let observed-agent one-of other players
To compare the payoffs and, if appropriate, set the value of the revising agent’s strategy-after-revision to the observed-agent’s strategy, we can write:
if ([payoff] of observed-agent) > payoff [ set strategy-after-revision ([strategy] of observed-agent) ]
This concludes the definition of the procedure to update-strategy-after-revision.
to update-strategy
In this procedure, the running player will just update her variable strategy with the value of her variable strategy-after-revision. The code is particularly simple:
to update-strategy set strategy strategy-after-revision end
5.6. Code in the plots
Finally, let us set up the plot to show the number of agents playing each strategy. This is something that can be done directly on the plot, in the Interface tab.
Edit the plot by right-clicking on it, choose a color and a name for the pen showing the number of agents with strategy 0, and in the “pen update commands” area write:
plot count players with [strategy = 0]
5.7. Final fix
In principle, we have finished our model but, unfortunately, we have a small mistake. If you run our code now, you will see that something weird seems to happen on the first tick (see figure 5). Too many agents seem to change their strategies on the first tick, even if prob-revision is set to 0! Can you figure out what is going on? This is a tricky bug, but no-one said that the life of a rigorous agent-based modeler was going to be easy. Here we do not give medals for free. You gotta earn them! 😀
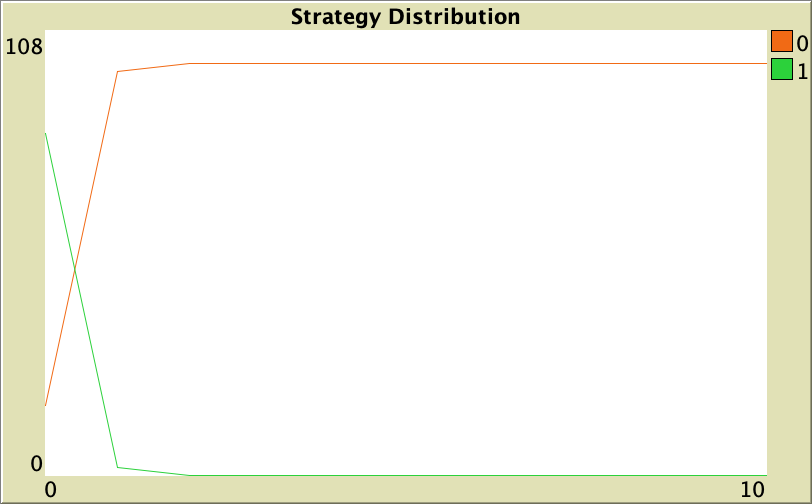
What is going on?
Well done if you ventured an answer! (even if your answer was wrong).
The problem with the current code is that we did not explicitly initialize the agents’ variable strategy-after-revision, and in NetLogo, by default, user-defined variables are initialized with the value 0. Then, on the first tick, every agent will run procedure to update-strategy (even if they do not happen to run procedure to update-strategy-after-revision before), so many agents will (incorrectly) set their strategy to 0.
To fix this problem, we just have to properly initialize agents’ variable strategy-after-revision when we create them, at procedure to setup:
to setup clear-all set payoff-matrix read-from-string payoffs create-players n-of-players [ set payoff 0 set strategy 0 ] ask n-of random (n-of-players + 1) players [set strategy 1] ask players [set strategy-after-revision strategy] ;; the line above is needed to guarantee that agents ;; keep their initial strategy until ;; they revise their strategy for the first time. ;; Note that all agents will set their strategy to ;; strategy-after-revision at the end of procedure to go. reset-ticks end
This concludes the definition of all the code in the Code tab, which by now should look as shown below.
5.8. Complete code in the Code tab
globals [ payoff-matrix ] breed [players player] players-own [ strategy strategy-after-revision payoff ] to setup clear-all set payoff-matrix read-from-string payoffs create-players n-of-players [ set payoff 0 set strategy 0 ] ask n-of random (n-of-players + 1) players [set strategy 1] ask players [set strategy-after-revision strategy] reset-ticks end to go ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick end to update-payoff let mate one-of other players set payoff item ([strategy] of mate) (item strategy payoff-matrix) end to update-strategy-after-revision let observed-player one-of other players if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] end to update-strategy set strategy strategy-after-revision end
6. Sample runs
Now that we have the model, we can investigate the question we posed at the motivation above. Let strategy 0 be “Defect” and let strategy 1 be “Cooperate”. We can use payoffs [[1 3][0 2]]. Note that we could choose any other numbers (as long as they satisfy the conditions that define a Prisoner’s Dilemma), since our decision rule only depends on ordinal properties of payoffs. Let us set n-of-players = 100 and prob-revision = 0.1, but feel free to change these values.
If you run the model with these settings, you will see that in nearly all runs all agents end up defecting in very little time.[4] The video below shows some representative runs.
Note that at any population state, defectors will tend to obtain a greater payoff than cooperators, so they will be preferentially imitated. Sadly, this drives the dynamics of the process towards overall defection.
7. Exercises
You can use the following link to download the complete NetLogo model: 2×2-imitate-if-better.nlogo.

Exercise 1. Consider a coordination game with payoffs [[3 0][0 2]] such that both players are better off if they coordinate in one of the actions (0 or 1) than if they play different actions. Run several simulations with 1000 players and probability of revision 0.1. (You can easily do that by leaving the button pressed down and clicking the button every time you want to start again from random initial conditions.)
Do simulations end up with all players choosing the same action? Does the strategy with a greater initial presence tend to displace the other strategy? How does changing the payoff matrix to [[30 0][0 2]] make a difference on whether agents coordinate on 0 or strategy 1?
P.S. You can explore this model’s (deterministic) mean dynamic approximation with this program.
Exercise 2. Consider a Stag hunt game (Skyrms, 2001) with payoffs [[3 0][2 1]] where strategy 0 is “Stag” and strategy 1 is “Hare”. Does the strategy with greater initial presence tend to displace the other strategy?
P.S. You can explore this model’s (deterministic) mean dynamic approximation with this program.

Exercise 3. Consider a Hawk-Dove game with payoffs [[0 3][1 2]] where strategy 0 is “Hawk” and strategy 1 is “Dove”. Do all players tend to choose the same strategy? Reduce the number of players to 100 and observe the difference in behavior (press the setup button after changing the number of players). Reduce the number of players to 10 and observe the difference.
P.S. You can explore this model’s (deterministic) mean dynamic approximation with this program.
Exercise 4. Create a stand-alone version of the model we have implemented in this chapter. To do this, you will have to upload the model to NetLogo Web and then export it in HTML format.
![]() Exercise 5. Reimplement the procedure to update-strategy-after-revision so the revising agent uses the imitative pairwise-difference rule that we saw in chapter I-2.
Exercise 5. Reimplement the procedure to update-strategy-after-revision so the revising agent uses the imitative pairwise-difference rule that we saw in chapter I-2.
![]() Exercise 6. Reimplement the procedure to update-strategy-after-revision so the revising agent uses the best experienced payoff rule that we saw in chapter I-2.
Exercise 6. Reimplement the procedure to update-strategy-after-revision so the revising agent uses the best experienced payoff rule that we saw in chapter I-2.
![]() Exercise 7. In our current model, agents compute their payoff by selecting another agent at random and playing the game. Note that this other (randomly selected) agent does not store the payoff of the interaction. By contrast, in some other evolutionary models, it is assumed that agents are randomly matched in pairs to play the game (with both members of the pair keeping record of the payoff obtained in the interaction). Can you think about how we could implement this alternative way of computing payoffs? We provide a couple of hints below:
Exercise 7. In our current model, agents compute their payoff by selecting another agent at random and playing the game. Note that this other (randomly selected) agent does not store the payoff of the interaction. By contrast, in some other evolutionary models, it is assumed that agents are randomly matched in pairs to play the game (with both members of the pair keeping record of the payoff obtained in the interaction). Can you think about how we could implement this alternative way of computing payoffs? We provide a couple of hints below:
Hints to implement random matching
- Naturally, the main changes will take place in procedure to update-payoff, but some other changes in the code may be necessary.
- In particular, we find it useful to define a new individually-owned variable named played?. For us, this is a boolean variable that keeps track of whether the agent has already played the game in the current tick or not. Thus, this variable would have to be set to false at the beginning of the tick (in procedure to go).
- The built-in reporter myself will be useful at the time of asking your mate to set her own payoff.
- This rule has been studied by Izquierdo and Izquierdo (2013) and Loginov (2021). Loginov (2021) calls this rule "imitate-the-better-realization". ↵
- By default, user-defined variables in NetLogo are initialized with the value 0, so there is no actual need to explicitly set the initial value of individually-owned variables to 0, but it does no harm either. ↵
- In some evolutionary models, it is assumed that players are randomly matched in pairs to play the game. That would lead to a slightly different distribution of payoffs (especially for low population sizes). In exercise 7, we ask you to think about the changes we would have to make in our current code to model this random matching. ↵
- All simulations will necessarily end up in one of the two absorbing states where all agents are using the same strategy. The absorbing state where everyone defects (henceforth D-state) can be reached from any state other than the absorbing state where everyone cooperates (henceforth C-state). The C-state can be reached from any state with at least two cooperators, so –in principle– any simulation with at least two agents using each strategy could end up in either absorbing state. However, it is overwhelmingly more likely that the final state will be the D-state. As a matter of fact, one single defector is extremely likely to be able to invade a whole population of cooperators, regardless of the size of the population. ↵

