Part IV. Games on networks
IV-1. The nxn game on a random network
1. Goal
The goal of this chapter is to learn how to implement models where players are connected in a network (see figure 1). A network is a set of nodes and a set of links.[1] Links connect pairs of nodes. In our models, the nodes in the network will be the players, so each link connects two players.
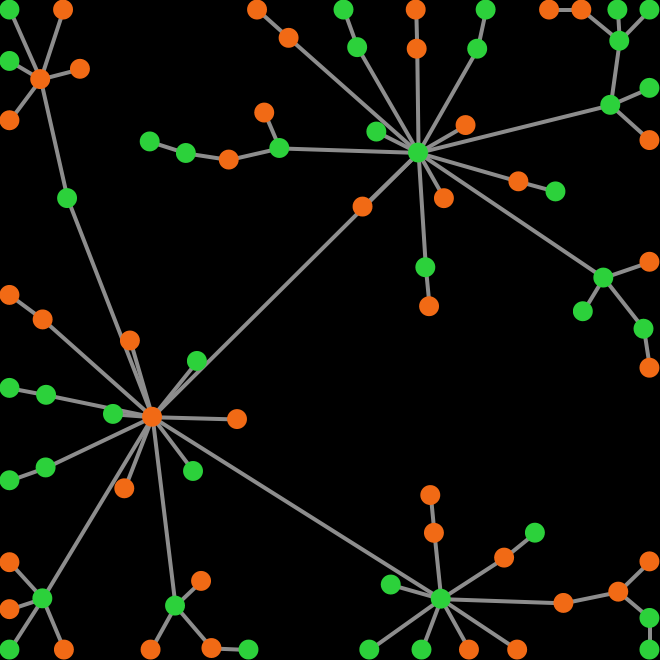
In this book, we will only use undirected links (which denote symmetric relations such as “being a sibling of”). Nonetheless, in NetLogo it is equally easy to implement models with directed links (for asymmetric relations, such as “being a parent of”), and also models with both types of links.
Here, we will use networks to limit the information that players can access. We assume that players can only interact with their link-neighbors (i.e. those with whom the player shares a link), so link-neighbors are the only players that a player can observe or play with. In this sense, networks define local neighborhoods of interaction, potentially different for each player.
By using networks, we will be able to generalize all the models previously developed in this book. Note that in Part II we implemented models where every player could observe and play with every other player. Such models can be interpreted as network models where players are connected through a complete network, i.e., a network where everyone is linked to everybody else. In Part III, we implemented models with spatial structure, i.e., models where players were embedded on a 2-dimensional grid and they could only interact with their spatial neighbors. Those models can be perfectly interpreted as network models. For instance, the spatial model where we used Von Neumann neighborhoods of radius 1 corresponds to a square lattice network. In this Part IV, we will learn to implement models where players are connected through any arbitrary network.
2. Motivation. A single-optimum coordination game
Consider the following 2-player 2-strategy single-optimum coordination game (which we discussed in chapter I-2):
| Player 2 | |||
| Player 2 chooses A | Player 2 chooses B | ||
| Player 1 | Player 1 chooses A | 1 , 1 | 0 , 0 |
| Player 1 chooses B | 0 , 0 | 2 , 2 | |
If you explore the dynamics of this game with the last model we developed in Part II, i.e. nxn-imitate-if-better-noise-efficient, you will see that a population of 100 agents using the imitate if better rule with low noise (e.g. noise = 0.03), starting with 70 A-strategists and 30 B-strategists, will almost certainly approach the inefficient state where everyone is choosing strategy A, and spend most of the time around it. In the video below, strategy A corresponds to strategy 0 (orange) and strategy B corresponds to strategy 1 (green).
Note that in every model developed in Part II, every player can observe and play with every other player (i.e., the network of potential interactions is complete). Now imagine that instead of assuming that everyone can interact with everyone, we assume that each player has just a few contacts (say about 2 on average), and we also asume that these contacts are set at random, in the sense that any possible contact exists with the same probability (i.e., an Erdős–Rényi random network).
Do you think that this change on the network of potential interactions (from complete, to sparse and random) will make any difference? Players will still select other players to observe and to play at random. The difference will be that the set of players with which each player can interact throughout the course of the simulation will be much smaller (though still random).
Let us build a model to explore this question!
3. Description of the model
We depart from the program we implemented in chapter II-3 (nxn-imitate-if-better-noise). In chapter II-4, we saw that the computational speed of this program could be greatly increased. However, the speed boost came at the expense of making our code slightly less readable. Here we want to focus on code readability, so we believe it is better to start with the most natural implementation of the model, i.e. nxn-imitate-if-better-noise.
The only change we are going to make to the model that nxn-imitate-if-better-noise implements is to embed the players on a network created following the G(n-of-players, prob-link) Erdős–Rényi random network model. In this type of network model, each possible link between any two players is included in the network with probability prob-link, independently from every other link. The following is a full description of the model we aim to implement, highlighting the main changes:
In this model, there is a population of n-of-players agents who repeatedly play a symmetric 2-player game with any number of strategies. The payoffs of the game are determined by the user in the form of a matrix [ [A00 A01 … A0n] [A10 A11 … A1n] … [An0 An1 … Ann] ] containing the payoffs Aij that an agent playing strategy i obtains when meeting an agent playing strategy j (i, j ∈ {0, 1, …, n}). The number of strategies is inferred from the number of rows in the payoff matrix.
The initial strategy distribution is set with parameter n-of-players-for-each-strategy, using a list of the form [a0 a1 … an], where item ai is the initial number of agents with strategy i. Thus, the total number of agents is the sum of all elements in this list.
Agents are embedded on a network created following the G(n-of-players, prob-link) Erdős–Rényi random network model. The network is created once at the beginning of the simulation and it is kept fixed for the whole simulation. Players can only interact with their link-neighbors in the network.
Once initial conditions are set and the network has been created, the following sequence of events –which defines a tick– is repeatedly executed:
- Every agent obtains a payoff by selecting one of her link-neighbors at random and playing the game.
- With probability prob-revision, individual agents are given the opportunity to revise their strategies. In that case, with probability noise, the revising agent will adopt a random strategy; and with probability (1 – noise), the revising agent will choose her strategy following the imitate if better rule, adapted for networks:
Look at one (randomly selected) link-neighbor and adopt her strategy if and only if her payoff was greater than yours. (And do nothing if you have no neighbors.)[2]
All agents who revise their strategies within the same tick do it simultaneously (i.e. synchronously).
The model shows the evolution of the number of agents choosing each of the possible strategies at the end of every tick. The model also shows a representation of the network, with players colored according to their strategies.
 4. Interface design
4. Interface design
We depart from the model we created in chapter II-3 (nxn-imitate-if-better-noise), so if you want to preserve it, now is a good time to duplicate it. The current interface looks as shown in figure II-3-1. Our goal now is to modify it so it looks as figure 2 below. We will place everything related to networks at the right side of the interface.

Let us go through all the necessary changes:
- We should bring forward the 2D view of the NetLogo world (i.e. the large black square) to a place where we can see it. We will use this view to represent the network of players.
Choose the dimensions of the world by clicking on the “Settings…” button on the top bar, by double-clicking on the 2D view, or by right-clicking on the 2D view and choosing Edit. A window will pop up, which allows you to choose the number of patches by setting the values of min-pxcor, max-pxcor, min-pycor and max-pycor. You can also determine the patches’ size in pixels, and whether the grid wraps horizontally, vertically, both or none (see Topology section).
We recommend unticking the boxes related to wrapping, to prevent the links of the network from going through the boundaries. Apart from that, feel free to choose any values you like for the other parameters. Our settings are shown in figure 3 below:
Figure 3. Model settings - Let us create two new buttons, for procedures that deal with the visualization of the network:
- One button named , which runs the procedure to relax-network indefinitely.
- One button named , which runs the procedure to drag-and-drop indefinitely.
In the Code tab, write the procedures to relax-network and to drag-and-drop, without including any code inside for now.
to relax-network ;; empty for now end to drag-and-drop ;; empty for now end
Then, create the buttons. Since these buttons deal only with visual aspects of the model, you may want to use the primitive with-local-randomness, which guarantees that this piece of code does not interfere with the generation of pseudorandom numbers for the rest of the model. Also, do not forget to tick the “Forever” option. When pressed, these buttons will make their respective procedures run repeatedly until the button is pressed again. We will understand later why we want this.
Figure 4. Settings for . Do not forget to tick on “Forever”
- Finally, let us create a slider to let the user choose the probability prob-link with which each link should be created in the random network.
Create a slider for global variable prob-link. You can choose limit values 0 (as the minimum) and 1 (as the maximum), and an increment of 0.01.
 5. Code
5. Code
5.1. Skeleton of the code
Figure 5 below provides a schematic view of the code. You can find the legend for code skeletons in Appendix A-2.
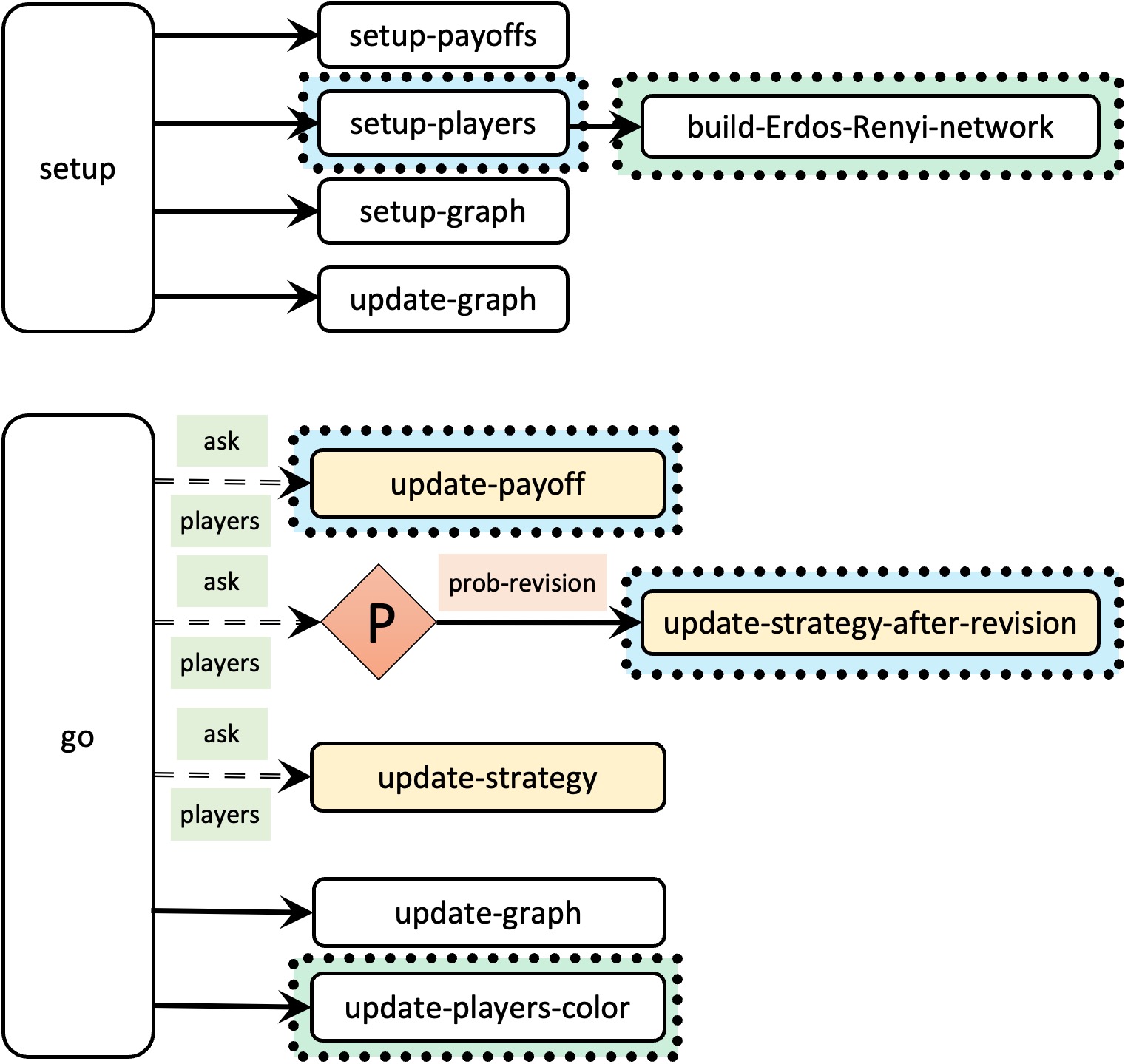
Note that the only differences between the skeleton of our current code and the skeleton of the new model we are creating now (fig. 5) are that:
- we are going to call a new procedure named to build-Erdos-Renyi-network when setting up the players (to build the random network),
- we are going to modify procedure to update-payoff so agents obtain their payoff by selecting one of her link-neighbors at random (rather than one other agent in the population at random),
- we are going to modify procedure to update-strategy-after-revision so revising agents look at one (randomly selected) link-neighbor (rather than at any other agent in the population), and
- we are going to call a new procedure named to update-players-color at the end of procedure to go, to color the players according to their strategy in the 2D view.
Let’s make it happen!!
5.2. Extensions, global variables and individually-owned variables
Extensions
To implement models with networks in NetLogo, there is a wonderful extension that will make our life much easier: the nw extension. It is highly recommended that you read its short documentation now. Then, to load the nw extension, write the following line at the very top of the code:
extensions [nw]
Global variables
There is no need to add or remove any global variables in our code. The current global variables are:
globals [ payoff-matrix n-of-strategies n-of-players ]
Individually-owned variables
There is no need to add or remove any individually-owned variables in our code. The current individually-owned variables are:
players-own [ strategy strategy-after-revision payoff ]
5.3. Setup procedures
In this model we want to embed the players in a G(n-of-players, prob-link) Erdős–Rényi random network. Thus, we should create a procedure to do that. We can call it to build-Erdos-Renyi-network. Primitive nw:generate-random from the nw extension builds the network for us. Thus, the code for this procedure is particularly easy:
to build-Erdos-Renyi-network nw:generate-random players links n-of-players prob-link end
To create the network, we have to specify the breed of turtles and the breed of links that will be used. Note that the command nw:generate-random will actually create new turtles and new links, from the breed that we specify. We want players to be the breed of turtles in our network and, since we have not defined a specific breed of links, we can just use the primitive links. To generate the network, we also have to specify the number of players we want to create, so we will have to make sure that variable n-of-players has the appropriate value at the time of calling procedure to build-Erdos-Renyi-network. Finally, prob-link is a parameter set by the user, so we do not have to worry about that.
Since procedure to build-Erdos-Renyi-network actually creates the players, we should call it from procedure to setup-players, which we can modify as follows:
to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] ;; we have to compute the number of players ;; before running procedure build-Erdos-Renyi-network set n-of-players sum initial-distribution ;; the following line is just for aesthetics set-default-shape players "circle" ;; now we build the network build-Erdos-Renyi-network ;; now we have created the players and the links ;; the following line is just for aesthetics ask players [fd 15] ;; the following lines ensure that ;; we set the initial distribution of strategies ;; according to initial-distribution ask players [set strategy -1] let i 0 foreach initial-distribution [ j -> ;; note that, below, we do not create the ;; players anymore (since they already exist) ask n-of j players with [strategy = -1] [ set payoff 0 set strategy i set strategy-after-revision strategy ] set i (i + 1) ] set n-of-players count players end
At this point, we can run our code and check that we have successfully created the network!
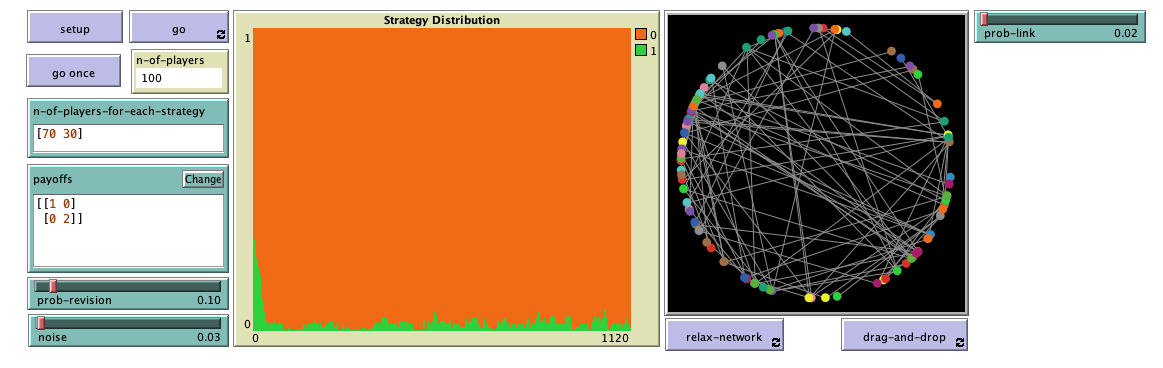
Even though we have successfully created the network, players can still observe and play with any other player in the population… but we will fix that in no time!
5.4. Go and other main procedures
In our model, we want players to interact only with their link-neighbors. In NetLogo, there is actually a primitive called link-neighbors, which we can use once we have created the network. Thus, in our code we should replace
other players
with the primitive link-neighbors at the places where we ask players to interact with other players. One such place is at procedure to update-payoff:
to update-payoff ;; let mate one-of other players <== deleted line let mate one-of link-neighbors ;; <== added line set payoff item ([strategy] of mate) (item strategy payoff-matrix) end
And the other place is at procedure to update-strategy-after-revision:
to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ ;; let observed player one-of other players <== deleted line let observed-player one-of link-neighbors ;; <== added line if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end
At this point, our code should not contain any syntactic errors. However, if you run it, you will get an error. Do you understand why? Can you fix it? The box below contains the solution. We hide it to give you a chance to experience the great satisfaction that comes when you accomplish something challenging.
Fix
Well done! Indeed, we sometimes ask players who have no neighbors to select one. We can easily fix this mistake using primitive any? as follows:
to update-payoff if any? link-neighbors [ ;; <== added line let mate one-of link-neighbors set payoff item ([strategy] of mate) (item strategy payoff-matrix) ] ;; <== added line end
to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ if any? link-neighbors [ ;; <== added line let observed-player one-of link-neighbors if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] ;; <== added line ] end
Now our program runs as desired. We just have to improve the visualization.
5.5 Other procedures
to update-players-color
We would like to color players according to their strategy. To keep our code modular, we will implement a separate procedure named to update-players-color for that. Can you code it?
Implementation of procedure to update-players-color
to update-players-color ask players [set color 25 + 40 * strategy] end
We should use the same colors for the strategies here as in the strategy plot, i.e. the colors that we set in procedure to setup-graph for the strategies.
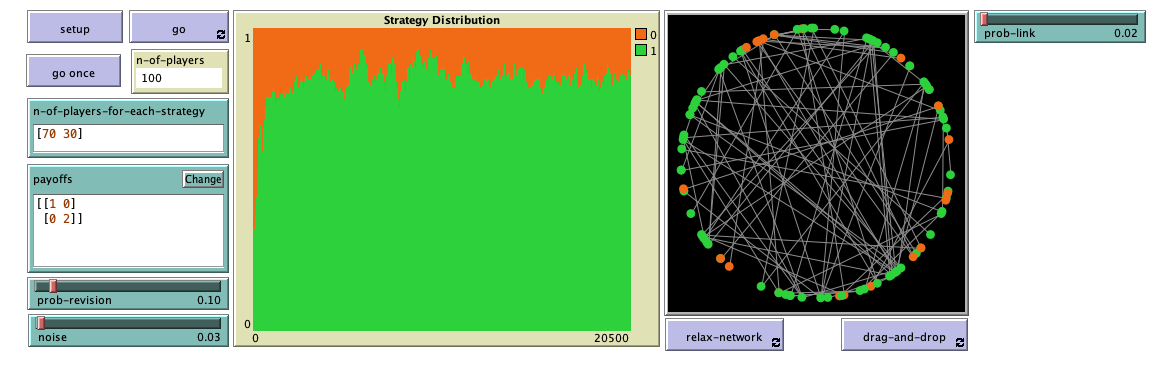
Once we have procedure to update-players-color implemented, we should call it both at the end of procedure to setup-players and of procedure to go. With this, we can run the model and see every individual player’s strategy (see fig. 7).
Visualization of the network: to relax-network and to drag-and-drop
Here we give the implementation of two procedures that will allow the user to visualize and inspect the network more easily. These are included in our code just for visualization purposes, and do not affect the behavior of the players.
Procedure to relax-network distributes the players on the world so they are not too close to each other. It is based on NetLogo’s primitive layout-spring. The following video shows its beautiful workings:
Procedure to drag-and-drop lets the user select one player with the mouse and move it around the world.
The credit for the code of these two procedures should go to Wilenski (2005a, 2005b) and his wonderful team.
;;;;;;;;;;;;;; ;;; Layout ;;; ;;;;;;;;;;;;;; ;; Procedures taken from Wilensky's (2005a) NetLogo Preferential ;; Attachment model ;; http://ccl.northwestern.edu/netlogo/models/PreferentialAttachment ;; and Wilensky's (2005b) Mouse Drag One Example ;; http://ccl.northwestern.edu/netlogo/models/MouseDragOneExample
to relax-network ;; the number 3 here is arbitrary; more repetitions slows down the ;; model, but too few gives poor layouts repeat 3 [ ;; the more players we have to fit into ;; the same amount of space, the smaller ;; the inputs to layout-spring we'll need to use let factor sqrt count players ;; numbers here are arbitrarily chosen for pleasing appearance layout-spring players links (1 / factor) (7 / factor) (3 / factor) display ;; for smooth animation ] ;; don't bump the edges of the world let x-offset max [xcor] of players + min [xcor] of players let y-offset max [ycor] of players + min [ycor] of players ;; big jumps look funny, so only adjust a little each time set x-offset limit-magnitude x-offset 0.1 set y-offset limit-magnitude y-offset 0.1 ask players [ setxy (xcor - x-offset / 2) (ycor - y-offset / 2) ] end to-report limit-magnitude [number limit] if number > limit [ report limit ] if number < (- limit) [ report (- limit) ] report number end to drag-and-drop if mouse-down? [ let candidate min-one-of players [distancexy mouse-xcor mouse-ycor] if [distancexy mouse-xcor mouse-ycor] of candidate < 1 [ ;; The WATCH primitive puts a "halo" around the watched turtle. watch candidate while [mouse-down?] [ ;; If we don't force the view to update, the user won't ;; be able to see the turtle moving around. display ;; The SUBJECT primitive reports the turtle being watched. ask subject [ setxy mouse-xcor mouse-ycor ] ] ;; Undoes the effects of WATCH. reset-perspective ] ] end
5.6. Complete code in the Code tab
extensions [nw] globals [ payoff-matrix n-of-strategies n-of-players ] breed [players player] players-own [ strategy strategy-after-revision payoff ] to setup clear-all setup-payoffs setup-players setup-graph reset-ticks update-graph end to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix end to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] set n-of-players sum initial-distribution set-default-shape players "circle" build-Erdos-Renyi-network ask players [fd 15] ask players [set strategy -1] let i 0 foreach initial-distribution [ j -> ask n-of j players with [strategy = -1] [ set payoff 0 set strategy i set strategy-after-revision strategy ] set i (i + 1) ] set n-of-players count players update-players-color end to build-Erdos-Renyi-network nw:generate-random players links n-of-players prob-link end to setup-graph set-current-plot "Strategy Distribution" foreach (range n-of-strategies) [ i -> create-temporary-plot-pen (word i) set-plot-pen-mode 1 set-plot-pen-color 25 + 40 * i ] end to go ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph update-players-color end to update-payoff if any? link-neighbors [ let mate one-of link-neighbors set payoff item ([strategy] of mate) (item strategy payoff-matrix) ] end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ if any? link-neighbors [ let observed-player one-of link-neighbors if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] ] end to update-strategy set strategy strategy-after-revision end to update-graph let strategy-numbers (range n-of-strategies) let strategy-frequencies map [ n -> count players with [strategy = n] / n-of-players ] strategy-numbers set-current-plot "Strategy Distribution" let bar 1 foreach strategy-numbers [ n -> set-current-plot-pen (word n) plotxy ticks bar set bar (bar - (item n strategy-frequencies)) ] set-plot-y-range 0 1 end to update-players-color ask players [set color 25 + 40 * strategy] end ;;;;;;;;;;;;;; ;;; Layout ;;; ;;;;;;;;;;;;;; ;; Procedures taken from Wilensky's (2005a) NetLogo Preferential ;; Attachment model ;; http://ccl.northwestern.edu/netlogo/models/PreferentialAttachment ;; and Wilensky's (2005b) Mouse Drag One Example ;; http://ccl.northwestern.edu/netlogo/models/MouseDragOneExample to relax-network ;; the number 3 here is arbitrary; more repetitions slows down the ;; model, but too few gives poor layouts repeat 3 [ ;; the more players we have to fit into ;; the same amount of space, the smaller ;; the inputs to layout-spring we'll need to use let factor sqrt count players ;; numbers here are arbitrarily chosen for pleasing appearance layout-spring players links (1 / factor) (7 / factor) (3 / factor) display ;; for smooth animation ] ;; don't bump the edges of the world let x-offset max [xcor] of players + min [xcor] of players let y-offset max [ycor] of players + min [ycor] of players ;; big jumps look funny, so only adjust a little each time set x-offset limit-magnitude x-offset 0.1 set y-offset limit-magnitude y-offset 0.1 ask players [ setxy (xcor - x-offset / 2) (ycor - y-offset / 2) ] end to-report limit-magnitude [number limit] if number > limit [ report limit ] if number < (- limit) [ report (- limit) ] report number end to drag-and-drop if mouse-down? [ let candidate min-one-of players [distancexy mouse-xcor mouse-ycor] if [distancexy mouse-xcor mouse-ycor] of candidate < 1 [ ;; The WATCH primitive puts a "halo" around the watched turtle. watch candidate while [mouse-down?] [ ;; If we don't force the view to update, the user won't ;; be able to see the turtle moving around. display ;; The SUBJECT primitive reports the turtle being watched. ask subject [ setxy mouse-xcor mouse-ycor ] ] ;; Undoes the effects of WATCH. reset-perspective ] ] end
6. Sample runs
Now that we have the model, we can investigate the question we posed at the motivation section above. If you run the model, you will see that, when embedded on a sparse random network, most players manage to eventually coordinate on the efficient strategy, achieving a much higher payoff than in the setting where they could interact with the whole population. To speed up your simulations, you can untick the “view updates” square at the Interface tab, and also make sure that none of the two network visualization buttons are down. The video below shows some representative runs.
This is a clear example of how network structure can impact evolutionary dynamics. The dynamics when players can only interact with a few neighbors are completely different from the dynamics when they can interact with the whole population.
7. Exercises
You can use the following link to download the complete NetLogo model: nxn-imitate-if-better-rd-nw.nlogo.
Exercise 1. Consider the single-optimum coordination game [[1 0][0 2]]. We have seen that a population of 100 agents embedded on a G(n-of-players = 100, prob-link = 0.02) Erdős–Rényi random network, using the imitate if better rule with noise = 0.03, prob-revision = 0.1, and starting with 70 A-strategists and 30 B-strategists, will most likely approach the efficient state where most players are choosing strategy B, and spend most of the time around it. Please, check this observation by running several simulations. (You can easily do that by leaving the button pressed down and clicking the button every time you want to start again.)
In this exercise, we ask you to assess the impact of prob-link (which determines the network density) on the proportion of players who choose strategy B. In particular, we would like to see a scatter plot with prob-link on the horizontal axis and the average proportion of B-strategists at tick 5000, across several runs, on the vertical axis.
Exercise 2. In exercise 1 above, how would changing the payoff matrix to [[1 0][0 20]] affect your answer?
Exercise 3. Using the same parameter values as in exercise 1 above, with prob-link = 0.04, the average proportion of B-strategists at tick 5000 is approximately 0.61. Does that mean that if you run a simulation and look at it at tick 5000, you can expect to see about 61% of agents choosing strategy B and the other 39% using strategy A?
![]() Exercise 4. Make the necessary changes in the code so players follow the imitate the best neighbor decision rule, which reads as follows:
Exercise 4. Make the necessary changes in the code so players follow the imitate the best neighbor decision rule, which reads as follows:
Hint to implement the imitate the best neighbor decision rule
You may want to revisit chapter III-1 of the book.
![]() Exercise 5. Repeat the experiment you conducted in exercise 1 above, now with the imitate the best neighbor rule, instead of the imitate if better rule adapted for networks. Before you see the results, make a guess about what you will observe.
Exercise 5. Repeat the experiment you conducted in exercise 1 above, now with the imitate the best neighbor rule, instead of the imitate if better rule adapted for networks. Before you see the results, make a guess about what you will observe.
![]() Exercise 6. Can you implement procedure to build-Erdos-Renyi-network without using the nw extension?
Exercise 6. Can you implement procedure to build-Erdos-Renyi-network without using the nw extension?
Hint to implement procedure to build-Erdos-Renyi-network without using the nw extension
You will have to use primitive create-links-with. Also, players’ who number may be useful to make sure that you only consider each pair of players once.
- A more mathematical term for network is "graph". People tend to use the term "graph" when they study the mathematical structure, composed only of nodes and links. The term "network", rather than graph, is often used when nodes or links have some individual attributes or properties that are of interest. In this book we will use the term "network", but do feel free to use the term "graph" if you like. In graph theory, nodes are often called "vertices" and links are often called "edges". ↵
- Note that, in this model, the agent observed by the revising agent may or may not be the same agent that the revising agent played with. In general, imposing that revising agents necessarily look at the same agent they played with leads to very different dynamics (see Hauert and Miȩkisz (2018)). ↵

