Part III. Spatial interactions on a grid
III-1. Spatial chaos in the Prisoner’s Dilemma
1. Goal
The goal of this chapter is to learn how to build agent-based models with spatial structure. In models with spatial structure, agents do not interact with all other agents with the same probability, but they interact preferentially with those who are nearby.[1]
More generally, populations where some pairs of agents are more likely to interact with each other than with others are called structured populations. This contrasts with the models developed in the previous Part, where all members of the population were equally likely to interact with each other.[2] The dynamics of an evolutionary process under random matching can be very different from the dynamics of the same process in a structured population. In social dilemmas in particular, population structure can play a crucial role (Gotts et al. (2003), Hauert (2002,[3] 2006), Roca et al. (2009a, 2009b)).[4]
2. Motivation. Cooperation in spatial settings
In the previous Part, we saw that if agents play the Prisoner’s Dilemma in a population where all members are equally likely to interact with each other, then defection prevails. Here we want to explore whether adding spatial structure may affect that observation. Could cooperation be sustained if we removed the unrealistic assumption that all members of the population are equally likely to interact with each other? To shed some light on this question, in this chapter we will implement a model analyzed by Nowak and May (1992, 1993).
3. Description of the model
In this model, there is a population of agents arranged on a 2-dimensional lattice of “patches”. There is one agent in each patch. The size of the lattice, i.e. the number of patches in each of the two dimensions, can be set by the user. Each patch has eight neighboring patches (i.e. the eight cells which surround it), except for the patches at the boundary, which have five neighbors if they are on a side, or three neighbors if they are at one of the four corners.
Agents repeatedly play a symmetric 2-player 2-strategy game, where the two possible strategies are labeled C (for Cooperate) and D (for Defect). The payoffs of the game are determined using four parameters: CC-payoff, CD-payoff, DC-payoff, and DD-payoff, where XY-payoff denotes the payoff obtained by an X-player who meets a Y-player.
The initial percentage of C-players in the population is initial-%-of-C-players, and they are randomly distributed in the grid. From then onwards, the following sequence of events –which defines a tick– is repeatedly executed:
- Every agent plays the game with all his neighbors (once with each neighbor) and with himself (Moore neighborhood). The total payoff for the player is the sum of the payoffs in these encounters.
- All agents simultaneously revise their strategy according to the imitate the best neighbor decision rule, which reads as follows:
Consider the set of all your neighbors plus yourself; then adopt the strategy of one of the agents in this set who has obtained the greatest payoff. If there is more than one agent with the greatest payoff, choose one of them at random to imitate.
 4. Interface design
4. Interface design
To define each agent’s neighborhood, in this chapter we will use the 2-dimensional grid already built in NetLogo, often called “the world”. This will make our code simpler and the visualizations nicer.
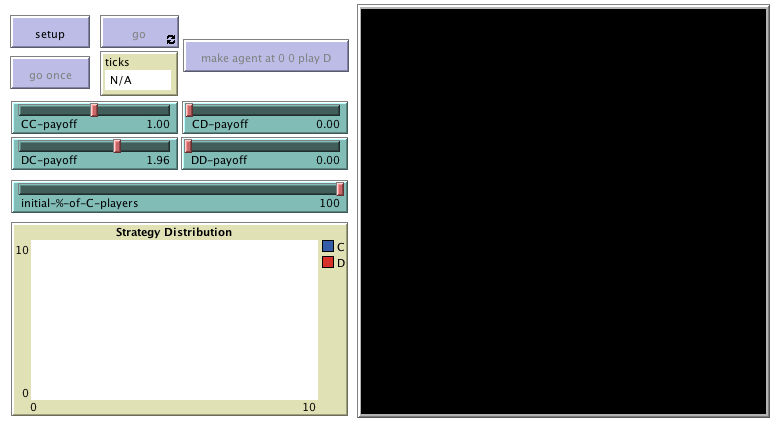
The interface (see figure 1 above) includes:
- The 2D view of the NetLogo world (i.e. the large black square in the interface), which is made up of patches. This view is already on the interface by default when creating a new NetLogo model.
Choose the dimensions of the world by clicking on the “Settings…” button on the top bar, or by right-clicking on the 2D view and choosing Edit. A window will pop up, which allows you to choose the number of patches by setting the values of min-pxcor, max-pxcor, min-pycor and max-pycor. You can also determine the patches’ size in pixels, and whether the grid wraps horizontally, vertically, both or none (see Topology section). You can choose these parameters as in figure 2 below:
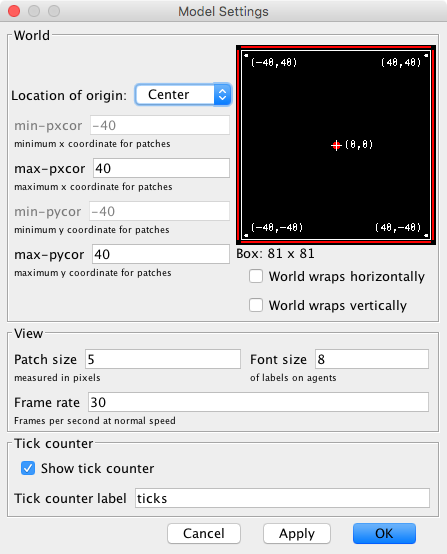
Figure 2. Model settings - Three buttons:
- One button named , which runs the procedure to setup.
- One button named , which runs the procedure to go.
- One button named , which runs the procedure to go indefinitely.
In the Code tab, write the procedures to setup and to go, without including any code inside for now. Then, create the buttons, just like we did in previous chapters.Note that the interface in figure 1 has an extra button labeled . You may wish to include it now. The code that goes inside this button is proposed as Exercise 2. - Four sliders, to choose the payoffs for each possible outcome (CC, CD, DC, DD).
Create the four sliders with global variable names CC-payoff, CD-payoff, DC-payoff, and DD-payoff. Remember to choose a range, an interval and a default value for each of them. You can choose minimum 0, maximum 2 and increment 0.01.
- A slider to let the user select the initial percentage of C-players.
Create a slider for global variable initial-%-of-C-players. You can choose limit values 0 (as the minimum) and 100 (as the maximum), and an increment of 1.
- A plot that will show the evolution of the number of agents playing each strategy.
Create a plot and name it Strategy Distribution.
 5. Code
5. Code
5.1. Skeleton of the code
Figure 3 below provides a schematic view of the code. You can find the legend for code skeletons in Appendix A-2.
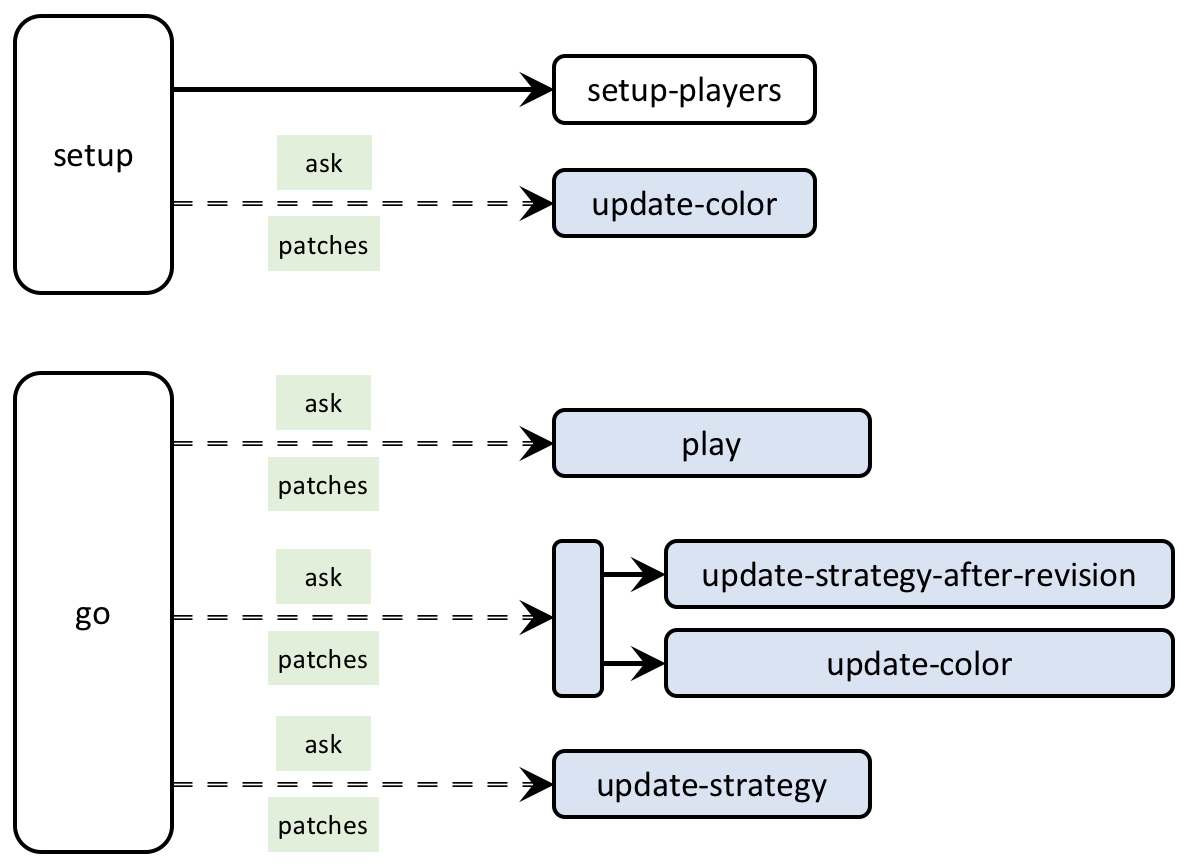
5.2. Global variables and individually-owned variables
We will not need any global variables besides those defined with the sliders in the interface.
Note that in this model there is a one-to-one correspondence between our immobile players and the patches they live in. Thus, there is no need to create any turtles (i.e. NetLogo mobile agents) in our model. We can work only with patches, and our code will be much simpler and readable.
Thus, we can make the built-in “patches” be the players, identifying each patch with one player. These patches already exist in NetLogo, making up the world, so we do not need to create them. Having said that, we do need to associate with each patch all the information that we want it to carry. This information will be:
- Whether the patch is a C-player or D-player. For efficiency and code readability we can use a boolean variable to this end, which we can call C-player? and which will take the value true or false.
- Whether the patch will be a C-player or a D-player after its revision. For this purpose, we may use the boolean variable C-player?-after-revision. This is needed because we want to model synchronous updating, i.e. we want all patches to change their strategy at the same time. To do this, first we will ask all patches to compute the strategy they will adopt after the revision and, once all patches have computed their next strategy, we will ask them all to switch to it at the same time.
- The total payoff obtained by the patch playing with its neighbours. We can call this variable payoff.
- For efficiency, it will also be useful to endow each patch with the set of neighbouring patches plus itself. The reason is that this set will be used many times, and it never changes, so it can be computed just once at the beginning and stored in memory. We will store this set in a variable named my-nbrs-and-me.
- The following variable is also defined for efficiency reasons. Note that the payoff of a patch depends on the number of C-players and D-players in its set my-nbrs-and-me. To spare the operation of counting D-players, we can calculate it as the number of players in my-nbrs-and-me (which does not change in the whole simulation) minus the number of C-players. To this end, we can store the number of players in the set my-nbrs-and-me of each patch as an individually-owned variable that we naturally name n-of-my-nbrs-and-me.
Thus, this part of the code looks as follows:
patches-own [ C-player? C-player?-after-revision payoff my-nbrs-and-me n-of-my-nbrs-and-me ]
5.3. Setup procedures
In the setup procedure we will:
- Clear everything up, so we initialize the model afresh, using the primitive clear-all:
clear-all - Set initial values for the variables that we have associated to each patch. We can set the payoff to 0,[5] and both C-player? and C-player-last? to false (later we will ask some patches to set these values to true). To set the value of my-nbrs-and-me, NetLogo primitives neighbors and patch-set are really handy.
ask patches [ set payoff 0 set C-player? false set C-player?-after-revision false set my-nbrs-and-me (patch-set neighbors self) set n-of-my-nbrs-and-me (count my-nbrs-and-me) ]
- Ask a certain number of randomly selected patches to be C-players. That number depends on the percentage initial-%-of-C-players chosen by the user and on the total number of patches, and it must be an integer, so we can calculate it as:
round (initial-%-of-C-players * count patches / 100)
To randomly select a certain number of agents from an agentset (such as patches), we can use the primitive n-of (which reports another –usually smaller– agentset). Thus, the resulting instruction will be:
ask n-of (round (initial-%-of-C-players * count patches / 100)) patches [ set C-player? true set C-player?-after-revision true ]
- Color patches according to the four possible combinations of values of C-player? and C-player?-after-revision. The color of a patch is controled by the NetLogo built-in patch variable pcolor. A first (and correct) implementation of this task could look like:
ask patches [ ifelse C-player?-after-revision [ ifelse C-player? [set pcolor blue] [set pcolor lime] ] [ ifelse C-player? [set pcolor yellow] [set pcolor red] ] ]
However, the following implementation, which makes use of NetLogo primitive ifelse-value is more readable, as one can clearly see that the only thing we are doing is to set the patch’s pcolor.
ask patches [ set pcolor ifelse-value C-player?-after-revision [ifelse-value C-player? [blue] [lime]] [ifelse-value C-player? [yellow] [red]] ]
- Reset the tick counter using reset-ticks.
Note that:
- Points 2 and 3 above are about setting up the players, so, to keep our code nice and modular, we could group them into a new procedure called to setup-players. This will make our code more elegant, easier to understand, easier to debug and easier to extend, so let us do it!
- The operation described in point 4 above will be conducted every tick, so we should create a separate procedure to this end that we can call to update-color, to be run by individual patches. Since this procedure is rather secondary (i.e. our model could run without this), we have a slight preference to place it at the end of our code, but feel free to do it as you like, since the order in which NetLogo procedures are written in the Code tab is immaterial.
Thus, the code up to this point should be as follows:
patches-own [ C-player? C-player?-after-revision payoff my-nbrs-and-me n-of-my-nbrs-and-me ] to setup clear-all setup-players ask patches [update-color] reset-ticks end to setup-players ask patches [ set payoff 0 set C-player? false set C-player?-after-revision false set my-nbrs-and-me (patch-set neighbors self) set n-of-my-nbrs-and-me (count my-nbrs-and-me) ] ask n-of (round (initial-%-of-C-players * count patches / 100)) patches [ set C-player? true set C-player?-after-revision true ] end to go end to update-color set pcolor ifelse-value C-player?-after-revision [ifelse-value C-player? [blue] [lime]] [ifelse-value C-player? [yellow] [red]] end
5.4. Go procedure
The procedure to go contains all the instructions that will be executed in every tick. In this particular model, we will ask each player (i.e. patch):
- To play with its neighbours in order to calculate its payoff. For modularity and clarity purposes, we should do this in a new procedure named to play.
- To compute the value of its next strategy and store it in the variable C-player?-after-revision. In this way, the variable C-player? will keep the strategy with which the current payoff has been obtained, and we can update the value of C-player?-after-revision without losing that information, which will be required by neighboring players when they compute their next strategy. To keep our code nice and modular, we will do this computation in a new procedure called to update-strategy-after-revision.
- To update its color according to their C-player? and C-player?-after-revision values, using the procedure to update-color.
- To update its strategy (i.e. the value of C-player?). We will do this in a separate new procedure called to update-strategy.
We should also mark the end of the round, or tick, after all players have updated their strategies, using the primitive tick, which increases the tick counter by one, and updates the graph on the interface. Thus, by now the code of procedure to go should look as follows:
to go ask patches [ play ] ask patches [ update-strategy-after-revision ;; here we are not updating the agent's strategy yet update-color ] ask patches [ update-strategy ] ;; now we update every agent's strategy at the same time tick end
5.5 Other procedures
to play
In procedure to play we want patches to calculate their payoff. This payoff will be the number of C-players in the set my-nbrs-and-me times the payoff obtained with a C-player, plus the number of D-players in the set times the payoff obtained with a D-player.
We will store the number of C-players in the set my-nbrs-and-me in a local variable that we can name n-of-C-players. The number can be computed as follows:
let n-of-C-players count my-nbrs-and-me with [C-player?]
Note that if the calculating patch is a C-player, the payoff obtained when playing with another C-player is CC-payoff, and if the calculating patch is a D-player, the payoff obtained when playing with a C-player is DC-payoff. Thus, in general, the payoff obtained when playing with a C-player can then be obtained using the following code:
ifelse-value C-player? [CC-payoff] [DC-payoff]
Similarly, the payoff obtained when playing with a D-player is:
ifelse-value C-player? [CD-payoff] [DD-payoff]
Taking all this into account, we can implement procedure to play as follows:[6]
to play let n-of-C-players count my-nbrs-and-me with [C-player?] set payoff n-of-C-players * (ifelse-value C-player? [CC-payoff] [DC-payoff]) + (n-of-my-nbrs-and-me - n-of-C-players) * (ifelse-value C-player? [CD-payoff] [DD-payoff]) end
to update-strategy-after-revision
In this procedure, which will be run by individual patches, we want the patch to compute its next strategy, which will be the strategy used by one of the patches with the maximum payoff in the set my-nbrs-and-me. To select one of these maximum-payoff patches, we may use primitives one-of and with-max as follows:
one-of (my-nbrs-and-me with-max [payoff])
Now remember that strategy updating in this model is synchronous, i.e. every player revises his strategy at the same time. Thus, we want each patch to adopt the strategy that was used by the selected maximum-payoff patch when it played the game, i.e. before any strategy revision may have taken place. This strategy is stored in variable C-player?. With this, we conclude the code of procedure to update-strategy-after-revision.
to update-strategy-after-revision set C-player?-after-revision [C-player?] of one-of my-nbrs-and-me with-max [payoff] end
Another (equivalent) implementation of this procedure, which makes use of primitive max-one-of is the following.
to update-strategy-after-revision set C-player?-after-revision [C-player?] of max-one-of my-nbrs-and-me [payoff] end
to update-strategy
This is a very simple procedure where the patch just updates its strategy (stored in variable C-player?) with the value of C-player?-after-revision. This update is not conducted right after having computed the value of C-player?-after-revision to make the strategy updating synchronous.
to update-strategy set C-player? C-player?-after-revision end
5.6. Complete code in the Code tab
The Code tab is ready!
patches-own [ C-player? C-player?-after-revision payoff my-nbrs-and-me n-of-my-nbrs-and-me ] to setup clear-all setup-players ask patches [update-color] reset-ticks end to setup-players ask patches [ set payoff 0 set C-player? false set C-player?-after-revision false set my-nbrs-and-me (patch-set neighbors self) set n-of-my-nbrs-and-me (count my-nbrs-and-me) ] ask n-of (round (initial-%-of-C-players * count patches / 100)) patches [ set C-player? true set C-player?-after-revision true ] end to go ask patches [ play ] ask patches [ update-strategy-after-revision ;; here we are not updating the agent's strategy yet update-color ] ask patches [ update-strategy ] ;; now we update every agent's strategy at the same time tick end to play let n-of-C-players count my-nbrs-and-me with [C-player?] set payoff n-of-C-players * (ifelse-value C-player? [CC-payoff] [DC-payoff]) + (n-of-my-nbrs-and-me - n-of-C-players) * (ifelse-value C-player? [CD-payoff] [DD-payoff]) end to update-strategy-after-revision set C-player?-after-revision [C-player?] of one-of my-nbrs-and-me with-max [payoff] end to update-strategy set C-player? C-player?-after-revision end to update-color set pcolor ifelse-value C-player?-after-revision [ifelse-value C-player? [blue] [lime]] [ifelse-value C-player? [yellow] [red]] end
5.7. Code in the plots
We will use blue color for the number of C-players and red for the number of D-players.
To complete the Interface tab, edit the graph and create the pens as in the image below:

6. Sample runs
We can use the model we have implemented to shed some light on the question that we posed at the motivation above. We will use the same parameter values as Nowak and May (1992), so we can replicate their results: CD-payoff = DD-payoff = 0, CC-payoff = 1, DC-payoff = 1.85, and initial-%-of-C-players = 90.[7] An illustration of the sort of patterns that this model generates is shown in the video below.
As you can see, both C-players and D-players coexist in this spatial environment, with clusters of both types of players expanding, colliding and fragmenting. The overall fraction of C-players fluctuates around 0.318 for most initial conditions (Nowak and May, 1992). Thus, we can see that adding spatial structure can make cooperation be sustained even in a population where agents can only play C or D (i.e. they cannot condition their actions on previous moves).
Incidentally, this model is also useful to see that a simple 2-player 2-strategy game in a two-dimensional spatial setting can generate chaotic and kaleidoscopic patterns (Nowak and May, 1993). To illustrate this, let us use the same payoff values as before, but let us start with all agents playing C, i.e. initial-%-of-C-players = 100.
When you click on , the whole world should look blue, since all agents are C-players. If you now click on , nothing should happen, since all agents are playing the same strategy and the strategy updating is imitative. To make things interesting, let us ask the agent at the center to play D. You can do this by typing the following code at the Command Center (i.e. the line at the bottom of the NetLogo screen) after clicking on :
ask patch 0 0 [set C-player? false]
If you now click on , you should see the following beautiful patterns:
7. Exercises
You can use the following link to download the complete NetLogo model: 2×2-imitate-best-nbr.nlogo.
Exercise 1. Let us run a (weak) Prisoner’s Dilemma game with payoffs DD-payoff = CD-payoff = 0, CC-payoff = 1 and DC-payoff = 1.7. Set the initial-%-of-cooperators to 90. Run the model and observe the evolution of the system as you gradually increase the value of DC-payoff from 1.7 to 2. If at any point all the players adopt the same strategy, press the button again to start a new simulation. Compare your observations with those in fig. 1 of Nowak and May (1992). Note: To use the same dimensions as Nowak and May (1992), you can change the location of the NetLogo world’s origin to the bottom left corner, and set both the max-pxcor and the max-pycor to 199. You may also want to change the patch size to 2.
![]() Exercise 2. Create a button to make the patch at 0 0 be a D-player. You may want to label it . This button will be useful to replicate some of the experiments in Nowak and May (1992, 1993).
Exercise 2. Create a button to make the patch at 0 0 be a D-player. You may want to label it . This button will be useful to replicate some of the experiments in Nowak and May (1992, 1993).
Exercise 3. Replicate the experiment shown in figure 3 of Nowak and May (1992). Note that you will have to make the NetLogo world be a 99 × 99 square lattice.
![]() Exercise 4. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
Exercise 4. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
With a small probability ε, each player errs and chooses evenly between strategies C and D; with probability 1-ε, the player follows the Nowak and May update rule.
You may wish to rerun the sample run above with a small value for ε. You may also want to replicate the experiment shown in Mukherji et al. (1996, fig. 1).
![]() Exercise 5. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
Exercise 5. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
During each period, players fail to update their previous strategy with a small probability, θ.
You may wish to rerun the sample run above with a small value for θ. You may also want to replicate the experiment shown in Mukherji et al. (1996, fig. 1).
![]() Exercise 6. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
Exercise 6. Implement the following extension to Nowak and May (1992)‘s model, proposed by Mukherji et al. (1996):
After following the Nowak and May update rule, each cooperator has a small independent probability, ϕ, of cheating by switching to defection.
You may wish to rerun the sample run above with a small value for ϕ. You may also want to replicate the experiment shown in Mukherji et al. (1996, fig. 1).
- Note that in most evolutionary models there are two types of neighborhoods for each individual agent A:
- the set of agents with whom agent A plays the game, and
- the set of agents that agent A may observe at the time of revising his strategy.
- Populations where all members are equally likely to interact with each other are sometimes called well-mixed populations. ↵
- See Roca et al. (2009b) for an important and illuminating discussion of this paper. ↵
- Christoph Hauert has an excellent collection of interactive tutorials on this topic at his site EvoLudo (Hauert 2018). ↵
- By default, user-defined variables in NetLogo are initialized with the value 0, so there is no actual need to explicitly set the initial value of individually-owned variables to 0, but it does no harm either. ↵
- The parentheses around the first ifelse-value block are necessary since NetLogo 6.1.0 (see https://ccl.northwestern.edu/netlogo/docs/transition.html#changes-for-netlogo-610). ↵
- Some authors make CD-payoff = DD-payoff, so they can parameterize the game with just one parameter, i.e. DC-payoff. Note, however, that the resulting game lies at the border between a Prisoner's Dilemma and a Hawk-Dove (aka Chicken or Snowdrift) game. Making CD-payoff = DD-payoff is by no means a normalization of the Prisoner's Dilemma, but a restriction which reduces the range of possibilities that can be studied. ↵

