V-2. A rather general model for games played in well-mixed populations

Luis R. Izquierdo; Segismundo S. Izquierdo; William H. Sandholm

Part V. Agent-based models vs ODE models

V-2. A rather general model for games played in well-mixed populations

1. Goal

The goal of this chapter is to extend the well-mixed population model we developed in chapter II-3 (nxn-imitate-if-better-noise) by adding two features that will make our program significantly more general:

The possibility to use expected payoffs. In all the models we developed in Part II, agents obtain their payoffs by playing with one agent, chosen at random. In this chapter we will allow agents to use expected payoffs. The expected payoff of strategy 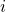$i$ is also the average payoff that an $i$ -strategist would obtain if she played with the whole population.
The possibility to model other decision rules besides the imitate if better rule.

2. Motivation

Once we have implemented different decision rules and the option to use expected payoffs, we will be able to model many different agent-based evolutionary dynamics. In the next chapter, we will develop the mean dynamic of each of these agent-based evolutionary dynamics, and we will see that they correspond to ODE models that have been studied in the literature.

3. Description of the model

We depart from the program we implemented in chapter II-3 (nxn-imitate-if-better-noise).^[1] You can find the full description of this model in chapter II-3. Our extension will include the following three additional parameters:

payoff-to-use. This parameter specifies the type of payoff that agents use in each tick. It will be implemented with a chooser, with two possible values:
- “play-with-one-rd-agent“: agents play with another agent chosen at random.
- “use-strategy-expected-payoff“: agents use their strategy’s expected payoff.
decision-rule. This parameter determines the decision rule that agents follow to update their strategies, just like in the models we developed in chapter III-4 and chapter IV-4. Note that all decision rules use the agents’ payoffs, and these are computed following the method prescribed by parameter payoff-to-use. Parameter decision-rule will be implemented with a chooser, with seven possible values:
- “imitate-if-better”. This is the imitate if better rule already implemented in the current model.
- “imitative-pairwise-difference”. This is the imitative pairwise-difference rule we saw in chapter I-2. Under this rule, the revising agent looks at another individual at random and considers imitating her strategy only if her payoff is greater than the reviser’s payoff; in that case, he switches with probability proportional to the payoff difference. In order to turn the payoff difference into a meaningful probability, we divide the payoff difference by the maximum possible payoff minus the minimum possible payoff.
- “imitative-linear-attraction”. Under this rule, the revising agent selects another individual at random and imitates her strategy with probability equal to the difference between the observed individual’s payoff and the minimum possible payoff, divided by the maximum possible payoff minus the minimum possible payoff. (The revising agent’s payoff is ignored.)
- “imitative-linear-dissatisfaction”. Under this rule, the revising agent selects another agent at random and imitates her strategy with probability equal to the difference between the maximum possible payoff and his own payoff, divided by the maximum possible payoff minus the minimum possible payoff. (The observed agent’s payoff is ignored.)
The four decision rules above are imitative, i.e. they all start by selecting one agent and consider imitating her strategy. In contrast, the following decision rules are direct (Sandholm, 2010a).^[2] Under direct decision rules, revising agents choose candidate strategies directly without looking at any agent, so a strategy’s popularity does not directly influence the probability with which it is considered. In the following direct decision rules, if payoff-to-use = “play-with-one-rd-agent“, each strategy is tested against one random individual, potentially different in each test.
- “direct-best”. The revising agent selects the strategy with the greatest payoff. Ties are resolved uniformly at random.
- “direct-pairwise-difference”. The revising agent randomly selects another strategy, and considers adopting it only if its payoff is greater; in that case, he switches with probability proportional to the payoff difference. In order to turn the difference in payoffs into a meaningful probability, we divide the payoff difference by the maximum possible payoff minus the minimum possible payoff.
- “direct-positive-proportional-m”. The revising agent selects one strategy at random, with probabilities proportional to payoffs raised to parameter m, and adopts it. Parameter m controls the intensity of selection (see below). We do not allow for negative payoffs when using this rule.
m. This is the parameter that controls the intensity of selection in decision rule direct-positive-proportional-m.

Everything else stays as described in chapter II-3.

4. Extension I. Implementation of different ways of computing payoffs

In this first extension, we just want to implement the option to use expected payoffs.

4.1. Skeleton of the code

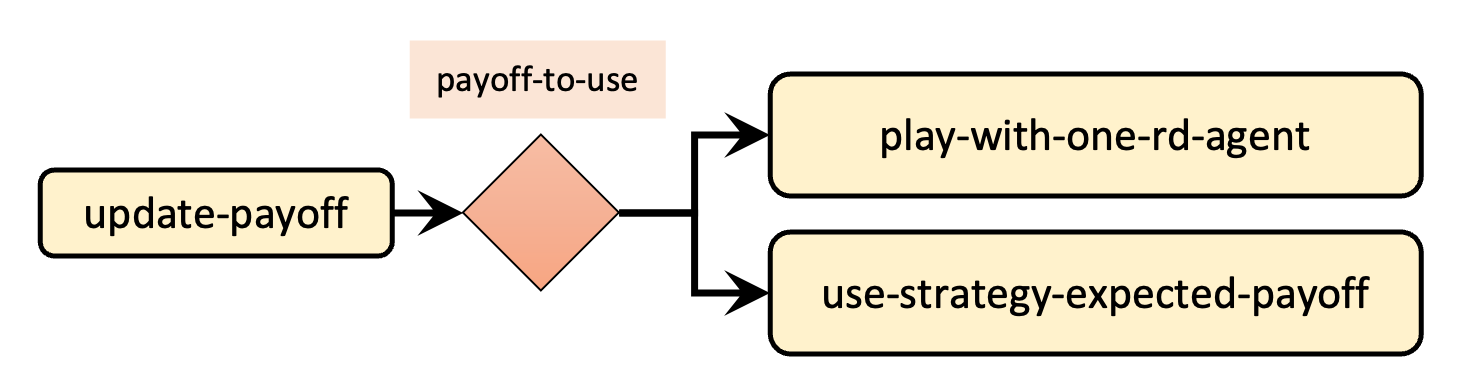
The main procedure we have to modify is to update-payoff, which is where payoffs are updated. Figure 1 below shows the skeleton of the new implementation of procedure to update-payoff.

Figure 1. Skeleton of procedure to update-payoff

4.2. Interface design

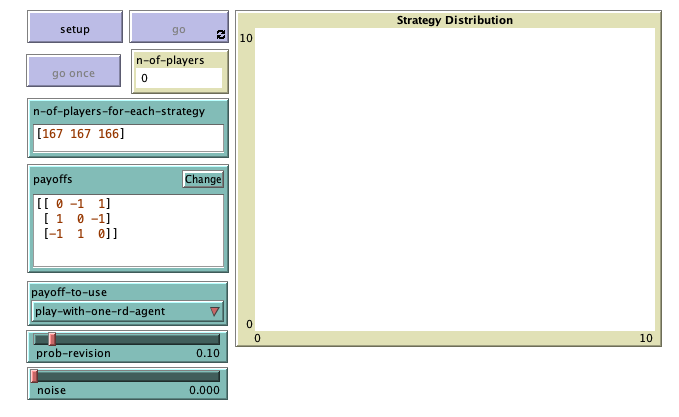
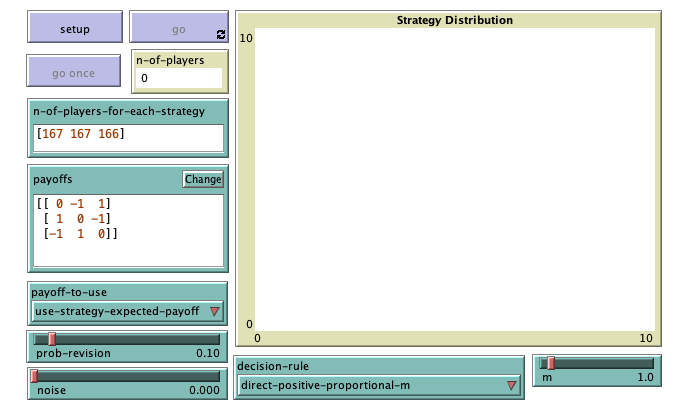
We depart from the model we created in chapter II-3 (nxn-imitate-if-better-noise), so if you want to preserve it, now is a good time to duplicate it. The current interface looks as shown in figure II-3-1. The only change we have to make to the interface is to add parameter payoff-to-use. We should add it as a chooser with possible values “play-with-one-rd-agent” and “use-strategy-expected-payoff“. The new interface should look as figure 2 below.

Figure 2. Interface design for the first extension

4.3. Code

4.3.1. Implementation of to update-payoff

The way payoffs are computed is determined by parameter payoff-to-use:

If payoff-to-use = “play-with-one-rd-agent“, agents play with another agent chosen at random.
If payoff-to-use = “use-strategy-expected-payoff“, agents use their strategy’s expected payoff.

A nice and modular way of implementing procedure to update-payoff is to create two new procedures, i.e., to play-with-one-rd-agent and to use-strategy-expected-payoff and call one or the other depending on the value of payoff-to-use (see skeleton in figure 1). Thus, the new code of to update-payoff could look as follows:

to update-payoff
  ifelse payoff-to-use = "play-with-one-rd-agent" 
    [play-with-one-rd-agent]
    [use-strategy-expected-payoff]
end

Given that we have chosen the names of the two new procedures to match the possible values of parameter payoff-to-use, we can also use run (a primitive that can take a string containing the name of a command as an input, and it runs the command) as follows:

to update-payoff
  run payoff-to-use
end

Our following step is to implement the two new procedures.

4.3.2. Implementation of to play-with-one-rd-agent

Note that in our baseline model nxn-imitate-if-better-noise, agents obtained a payoff by playing with another agent chosen at random. Thus, for the implementation of to play-with-one-rd-agent, we can just use the code that we previously had in procedure to update-payoff:

to play-with-one-rd-agent
  let mate one-of other players
  set payoff item ([strategy] of mate) (item strategy payoff-matrix)
end

4.3.3. Implementation of to use-strategy-expected-payoff

This new procedure should assign the appropriate expected payoff to the agent who runs it. Note that we do not want every agent to compute the expected payoff of their strategy. This would be inefficient because there are usually many more agents than strategies. Instead, we should compute the expected payoff of each strategy just once in each tick, and have these payoffs ready for agents to read.

We will implement a procedure to compute expected payoffs in the next section, but for now, let us assume that these expected payoffs are available to agents in a global variable called strategy-expected-payoffs. This variable will contain a list with the expected payoff of each strategy, in order. Assuming that, the code for procedure to use-strategy-expected-payoff is particularly simple:

to use-strategy-expected-payoff
  set payoff item strategy strategy-expected-payoffs
end

4.3.4. Implementation of to update-strategy-expected-payoffs

Our goal now is to code the procedure in charge of computing the expected payoff for each strategy and of storing them in a global variable named strategy-expected-payoffs. Let us call this new procedure to update-strategy-expected-payoffs, and work through the logic together.

It is often easier to start with a concrete example and then try to generalize. Let us start by thinking how to compute the expected payoff of strategy 0. To do this, we need the payoffs that strategy 0 can obtain (e.g., [0 -1 1] in figure 2) and we need the frequencies of each strategy in the population (e.g. [0.2 0.3 0.5]). Then, we would only have to multiply the two lists element by element ( [ 0*0.2 -1*0.3 1*0.5 ] ) and sum all the elements of the resulting list (0*0.2 + -1*0.3 + 1*0.5).

Our current code already computes the frequencies of each strategy in procedure to update-graph, so we already have the code for that:

let strategy-frequencies map [ n ->
      count players with [strategy = n] / n-of-players
    ] strategy-numbers

Assuming we have the strategy frequencies stored in strategy-frequencies, to compute the expected payoff of strategy 0 in our example we would only have to do:

sum (map * [ 0 -1 1 ] strategy-frequencies)

Now is the time to generalize. To compute the expected payoff of each of the strategies, we just have to apply the code snippet above to the list of payoffs of each strategy. Note that the payoff matrix contains precisely the lists of payoffs for each strategy, so we can use map as follows:

set strategy-expected-payoffs map [ list-of-payoffs ->
    sum (map * list-of-payoffs strategy-frequencies) 
    ] payoff-matrix

As mentioned before, since we want agents to be able to read the strategy expected payoffs, we should define variable strategy-expected-payoffs as global. Also, there is no point in computing the strategies frequencies more than once in each tick, so we should also define strategy-frequencies as a global variable, and update it only in one place. And finally, now we will be using the strategy numbers at two places (procedures to update-strategy-expected-payoffs and to update-graph), so we could also define strategy-numbers as a global variable:

globals [
  payoff-matrix
  n-of-strategies
  n-of-players

  strategy-numbers          ;; <= new global variable
  strategy-frequencies      ;; <= new global variable
  strategy-expected-payoffs ;; <= new global variable
]

With all this, the code for procedure to update-strategy-expected-payoffs would be:

to update-strategy-expected-payoffs
  set strategy-frequencies map [ n ->
        count players with [strategy = n] / n-of-players
      ] strategy-numbers
  set strategy-expected-payoffs map [ list-of-payoffs ->
      sum (map * list-of-payoffs strategy-frequencies) ] payoff-matrix
end

Since we are updating strategy-frequencies in this procedure, and the variable is now global, we can remove that computation from procedure to update-graph. Similarly, since variable strategy-numbers is now global and its value does not change over the course of a simulation run, we should move its computation from to update-graph to a setup procedure, such as to setup-payoffs:

to update-graph
; let strategy-numbers (range n-of-strategies)
; let strategy-frequencies map [ n ->
;      count players with [strategy = n] / n-of-players
;     ] strategy-numbers

set-current-plot "Strategy Distribution"
  let bar 1
  foreach strategy-numbers [ n ->
    set-current-plot-pen (word n)
    plotxy ticks bar
    set bar (bar - (item n strategy-frequencies))
  ]
  set-plot-y-range 0 1
end

to setup-payoffs
  set payoff-matrix read-from-string payoffs
  set n-of-strategies length payoff-matrix
  set strategy-numbers range n-of-strategies  ;; <= new line
end

Now, we should make sure that we call procedure to update-strategy-expected-payoffs (where strategy-frequencies is updated) before running procedure to update-graph, where these frequencies are used. We do that at procedures to setup and to go. We also take this opportunity to improve the efficiency of the model by including the primitive no-display in procedure to setup, right after clear-all.

to setup
  clear-all
  no-display ;; <= new line to improve efficiency
  setup-payoffs
  setup-players
  setup-graph
  reset-ticks
  update-strategy-expected-payoffs ;; <= new line
  update-graph
end

to go
  ask players [update-payoff]

  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]
  tick
 
  update-strategy-expected-payoffs ;; <= new line
  update-graph
end

Finally, note that, since procedure to update-strategy-expected-payoffs is called from to go, we know that variable strategy-expected-payoffs is updated in every tick, as required.

There is a subtle final issue here. We have to make sure that, given a certain population state (i.e. once agents have updated their strategies), variable strategy-expected-payoffs is updated before agents update their payoffs in procedure to update-payoff. Note that this is so in our current code, even at the first tick (since procedure to update-strategy-expected-payoffs is called from to setup too). In other words, whenever agents update their payoffs, variable strategy-expected-payoffs contains the updated expected payoffs, i.e., the ones corresponding to the current population state.

Table 1 below shows a sketch of the order in which the main procedures are executed in a simulation run. The lines highlighted in yellow indicate when the population state changes. Note that, in between highlighted lines, procedure to update-strategy-expected-payoffs is executed before agents update their payoffs in procedure to update-payoff.

↓	setup	↓	……..	;; <= various setup procedures
↓		↓	update-strategy-expected-payoffs
↓		↓	update-graph
↓	go	↓	ask players [update-payoff]
↓		↓	……..	;; <= agents update strategy-after-revision
↓		↓	ask players [update-strategy]	;; <= change of population state
↓		↓	tick
↓		↓	update-strategy-expected-payoffs
↓		↓	……..	;; <= update-graph
↓	go	↓	ask players [update-payoff]
↓		↓	……..	;; <= agents update strategy-after-revision
↓		↓	ask players [update-strategy]	;; <= change of population state
↓		↓	tick
↓		↓	update-strategy-expected-payoffs
↓		↓	……..	;; <= update-graph
↓	go	↓	ask players [update-payoff]
↓		↓	……..	;; <= agents update strategy-after-revision
↓		↓	ask players [update-strategy]	;; <= change of population state
↓		↓	tick
↓		↓	update-strategy-expected-payoffs
↓		↓	……..	;; <= update-graph

Table 1. Sketch of the order in which the main procedures are executed in a simulation run

4.3.5. Final checks

We can conduct a few simple checks to gain confidence in our code. For instance, to see the different payoffs that 0-strategists obtain, we can include the following line in procedure to go, right after agents update their payoffs:

  show remove-duplicates [payoff] of players with [strategy = 0]

to go
  ask players [update-payoff]
  show remove-duplicates [payoff] of players with [strategy = 0]
  
  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]
  tick
  update-strategy-expected-payoffs
  update-graph
end

With this code in place, please, try to answer the four questions below:

1. Can you find out what we should see in the command center if we click on setup and then on go once with the setting shown in figure 2?

Since payoff-to-use = “play-with-one-rd-agent“, agents play with another agent chosen at random. Thus, most likely, some 0-strategists will meet another 0-strategist (and obtain a payoff of 0), some will meet a 1-strategist (and obtain a payoff of -1), and some will meet a 2-strategist (and obtain a payoff of 1). Therefore, almost for certain we will see a list containing these three payoffs [0 -1 1], in any order.

2. And if we change payoff-to-use to = “use-strategy-expected-payoff“?

The payoff for all 0-strategists is now the expected payoff of strategy 0, so we should only see one number in the list. At the initial state, this number should be:
(0*(167/500) + -1*(167/500) + 1*(166/500)) = -1/500 = -0.002
We actually see [-0.0020000000000000018] due to floating-point errors.

3. What should we observe if we remove with [strategy = 0] from the line we added in procedure to go, still using payoff-to-use to = “use-strategy-expected-payoff“?

We should see a list containing the three expected payoffs, in any order. At the initial state, these payoffs are:
( 0*(167/500) + -1*(167/500) + 1*(166/500)) = -1/500 = -0.002
( 1*(167/500) + 0*(167/500) + -1*(166/500)) = 1/500 = 0.002
(-1*(167/500) + 1*(167/500) + 0*(166/500)) = 0

We actually see [0 0.0020000000000000018 -0.0020000000000000018] due to floating-point errors.

4. And if we now change payoff-to-use to = “play-with-one-rd-agent“?

Almost certainly, we will see a list containing the three payoffs [0 -1 1], in any order.

4.4. Complete code of Extension I in the Code tab

Well done! We have now finished the first extension! You can use the following link to download the complete NetLogo model: nxn-imitate-if-better-noise-payoff-to-use.nlogo.

globals [
  payoff-matrix
  n-of-strategies
  n-of-players
  strategy-numbers          ;; <= new global variable
  strategy-frequencies      ;; <= new global variable
  strategy-expected-payoffs ;; <= new global variable
]

breed [players player]

players-own [
  strategy
  strategy-after-revision
  payoff
]

;;;;;;;;;;;;;
;;; SETUP ;;;
;;;;;;;;;;;;;

to setup
  clear-all
  no-display ;; <= new line to improve efficiency
  setup-payoffs
  setup-players
  setup-graph
  reset-ticks
  update-strategy-expected-payoffs ;; <= new line
  update-graph
end

to setup-payoffs
  set payoff-matrix read-from-string payoffs
  set n-of-strategies length payoff-matrix
  set strategy-numbers range n-of-strategies  ;; <= new line
end

to setup-players
  let initial-distribution read-from-string n-of-players-for-each-strategy
  if length initial-distribution != length payoff-matrix [
    user-message (word "The number of items in\n"
      "n-of-players-for-each-strategy (i.e. "
      length initial-distribution "):\n"
      n-of-players-for-each-strategy
      "\nshould be equal to the number of rows\n"
      "in the payoff matrix (i.e. "
      length payoff-matrix "):\n"
      payoffs
    )
  ]

  let i 0
  foreach initial-distribution [ j ->
    create-players j [
      set payoff 0
      set strategy i
      set strategy-after-revision strategy
    ]
    set i (i + 1)
  ]

  set n-of-players count players
end

to setup-graph
  set-current-plot "Strategy Distribution"
  foreach (range n-of-strategies) [ i ->
    create-temporary-plot-pen (word i)
    set-plot-pen-mode 1
    set-plot-pen-color 25 + 40 * i
  ]
end

;;;;;;;;;;
;;; GO ;;;
;;;;;;;;;;

to go
  ask players [update-payoff]
  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]
  tick
  update-strategy-expected-payoffs ;; <= new line
  update-graph
end

;;;;;;;;;;;;;;;;;;;;;;
;;; UPDATE PAYOFFS ;;;
;;;;;;;;;;;;;;;;;;;;;;

to update-strategy-expected-payoffs
  set strategy-frequencies map [ n ->
        count players with [strategy = n] / n-of-players
      ] strategy-numbers
  set strategy-expected-payoffs map [ list-of-payoffs ->
      sum (map * list-of-payoffs strategy-frequencies) ] payoff-matrix
end

to update-payoff
  run payoff-to-use
end

to play-with-one-rd-agent
  let mate one-of other players
  set payoff item ([strategy] of mate) (item strategy payoff-matrix)
end

to use-strategy-expected-payoff
  set payoff item strategy strategy-expected-payoffs
end

;;;;;;;;;;;;;;;;;;;;;;;;;
;;; UPDATE STRATEGIES ;;;
;;;;;;;;;;;;;;;;;;;;;;;;;

to update-strategy-after-revision
  ifelse random-float 1 < noise
    [ set strategy-after-revision (random n-of-strategies) ]
    [
      let observed-player one-of other players
      if ([payoff] of observed-player) > payoff [
        set strategy-after-revision ([strategy] of observed-player)
      ]
    ]
end

to update-strategy
  set strategy strategy-after-revision
end

;;;;;;;;;;;;;;;;;;;;
;;; UPDATE GRAPH ;;;
;;;;;;;;;;;;;;;;;;;;

to update-graph
  ; let strategy-numbers (range n-of-strategies)
  ; let strategy-frequencies map [ n ->
  ;      count players with [strategy = n] / n-of-players
  ;    ] strategy-numbers

  set-current-plot "Strategy Distribution"
  let bar 1
  foreach strategy-numbers [ n ->
    set-current-plot-pen (word n)
    plotxy ticks bar
    set bar (bar - (item n strategy-frequencies))
  ]
  set-plot-y-range 0 1
end

5. Extension II. Implementation of different decision rules

In our second extension, we will implement the following procedures, one for each decision rule:

to imitate-if-better-rule
to imitative-pairwise-difference-rule
to imitative-linear-attraction-rule
to imitative-linear-dissatisfaction-rule
to direct-best-rule
to direct-pairwise-difference-rule
to direct-positive-proportional-m-rule

Note that we have chosen the name of the procedures to match the possible values of parameter decision-rule (plus the suffix “-rule”).

5.1. Skeleton of the code

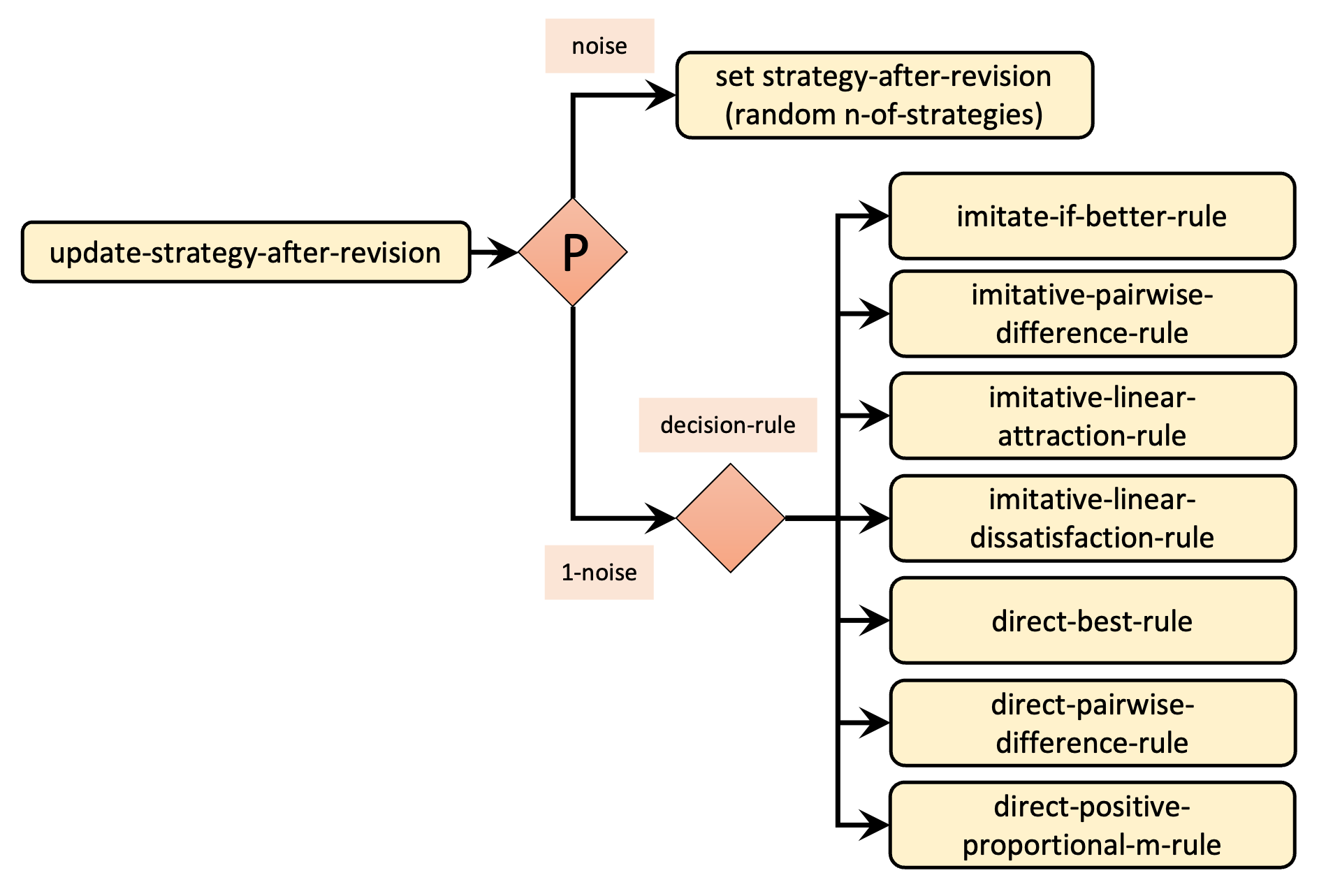
The main procedure we have to modify is to update-strategy-after-revision, which is where the different decision rules are called from. Figure 3 below shows the skeleton of the new implementation of procedure to update-strategy-after-revision.

Figure 3. Skeleton of procedure to update-strategy-after-revision

5.2. Interface design

The current interface looks as shown in figure 2. The only change we have to make to the interface is to add the following parameters:

decision-rule. We can add it as a chooser with possible values “imitate-if-better“, “imitative-pairwise-difference“, “imitative-linear-attraction“, “imitative-linear-dissatisfaction“, “direct-best”, “direct-pairwise-difference”, and “direct-positive-proportional-m”.
m. We can add it as a slider (with minimum = 0 and increment = 0.1).

The new interface should look as figure 4 below.

Figure 4. Interface design for the first extension

5.3. Code

5.3.1. Global variables

For some decision rules, agents will need access to the minimum and the maximum possible payoffs, and to the maximum possible payoff difference. For this reason, it makes sense to define these as global variables.

globals [
  payoff-matrix
  n-of-strategies
  n-of-players
  strategy-numbers
  strategy-frequencies
  strategy-expected-payoffs

  min-of-payoff-matrix  ;; <= new global variable
  max-of-payoff-matrix  ;; <= new global variable
  max-payoff-difference ;; <= new global variable
]

Since the value of these global variables will not change over the course of a simulation run, we should set them at a setup procedure. The most appropriate place is at procedure to setup-payoffs.

to setup-payoffs
  set payoff-matrix read-from-string payoffs
  set n-of-strategies length payoff-matrix
  set strategy-numbers range n-of-strategies

  ;; new lines below
  set min-of-payoff-matrix min reduce sentence payoff-matrix
  set max-of-payoff-matrix max reduce sentence payoff-matrix
  set max-payoff-difference (max-of-payoff-matrix - min-of-payoff-matrix)
end

5.3.2. Implementation of to update-strategy-after-revision

Let us start with the implementation of procedure to update-strategy-after-revision. Given the names we have chosen for the procedures for the different decision rules (see skeleton in Figure 3), can you venture a simple implementation for our new procedure to update-strategy-after-revision using primitive run?

Implementation of procedure to update-strategy-after-revision

to update-strategy-after-revision
  ifelse random-float 1 < noise
    [ set strategy-after-revision (random n-of-strategies) ]
    [ run (word decision-rule "-rule") ]
end

Now we just have to implement the procedures for each of the seven decision rules. If you have managed to follow this book up until here, you are most likely ready to implement them by yourself!

5.3.3. Imitative decision rules

Implementation of to imitate-if-better-rule

This is the decision rule we had implemented in our baseline model nxn-imitate-if-better-noise, so we can just copy the code.

Implementation of procedure to imitate-if-better-rule

to imitate-if-better-rule
  let observed-player one-of other players

  if ([payoff] of observed-player) > payoff [
    set strategy-after-revision ([strategy] of observed-player)
  ]
end

Implementation of to imitative-pairwise-difference-rule

To implement this rule, the code we wrote in chapter III-4 will be very useful.

Implementation of procedure to imitative-pairwise-difference-rule

to imitative-pairwise-difference-rule
  let observed-player one-of other players

  ;; compute difference in payoffs
  let payoff-diff ([payoff] of observed-player - payoff)

  set strategy-after-revision ifelse-value
    (random-float 1 < (payoff-diff / max-payoff-difference))
      [ [strategy] of observed-player ]
      [ strategy ]
    ;; If your strategy is the better, payoff-diff is negative,
    ;; so you are going to stick with it.
    ;; If it's not, you switch with probability
    ;; (payoff-diff / max-payoff-difference)
end

Implementation of to imitative-linear-attraction-rule

Can you try to implement this rule by yourself?

Implementation of procedure to imitative-linear-attraction-rule

to imitative-linear-attraction-rule
  let observed-player one-of players

  set strategy-after-revision ifelse-value
    (random-float 1 <
           ([payoff] of observed-player - min-of-payoff-matrix) /
           ( max-of-payoff-matrix - min-of-payoff-matrix) )
      [ [strategy] of observed-player ]
      [ strategy ]
end

Implementation of to imitative-linear-dissatisfaction-rule

The code for this rule is similar to the previous one. Can you implement it?

Implementation of procedure to imitative-linear-dissatisfaction-rule

to imitative-linear-dissatisfaction-rule
  let observed-player one-of players

  set strategy-after-revision ifelse-value
    (random-float 1 <
           (max-of-payoff-matrix - payoff) /
           (max-of-payoff-matrix - min-of-payoff-matrix) )
      [ [strategy] of observed-player ]
      [ strategy ]
end

5.3.4. Direct decision rules

In this section, we implement three direct decisions rules: “direct-best”, “direct-pairwise-difference”, and “direct-positive-proportional-m”. In direct decision rules, agents consider different candidate strategies, and choose one of them based on their assigned payoffs. Thus, the first thing we should do is to implement a procedure that assigns payoffs to strategies.

Assigning payoffs to strategies

The payoff assigned to each strategy is determined by parameter payoff-to-use:

If payoff-to-use = “play-with-one-rd-agent“, the payoff assigned to strategy 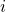$i$ will be the payoff resulting from trying out strategy 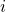$i$ against one agent chosen at random from the population. Importantly, according to the description of the model, every time a strategy is tested by a reviser, it should be tested against a newly (randomly) drawn agent.
If payoff-to-use = “use-strategy-expected-payoff“, the payoff assigned to strategy 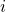$i$ will be strategy 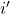$i'$ s expected payoff.

Our goal now is to implement a reporter named to-report payoff-for-strategy [ $s$ ], which takes a strategy number $s$ as an input, and returns the appropriate payoff for strategy $s$ , taking into account the current value of parameter payoff-to-use. Bearing in mind that strategies’ expected payoffs are stored in global variable strategy-expected-payoffs, can you implement to-report payoff-for-strategy?

Implementation of reporter to-report payoff-for-strategy

to-report payoff-for-strategy [s]
  report ifelse-value payoff-to-use = "play-with-one-rd-agent"
    [item ([strategy] of one-of other players) (item s payoff-matrix)]
    [item s strategy-expected-payoffs]
end

Implementation of to direct-best-rule

To implement this rule, it is useful to create a list of two-item lists (i.e., a list of pairs) that we can call pairs-strategy-payoff. In this list, there will be one pair for each strategy. The first item in each pair will be the strategy number and the second item will be the payoff assigned to that strategy:

let pairs-strategy-payoff (map [
    [s] -> list s (payoff-for-strategy s)
  ] strategy-numbers)

With this list in place, you can use primitive sort-by to select one of the pairs with the highest payoff. Remember that ties should be resolved at random. Admittedly, implementing this procedure is not easy, so if you manage to do it, you can certainly give yourself a pat on the back!

Implementation of procedure to direct-best-rule

to direct-best-rule
  let pairs-strategy-payoff (map [
    [s] -> list s (payoff-for-strategy s)
  ] strategy-numbers)

  ;; the following line ensures that ties
  ;; are resolved (uniformly) at random
  set pairs-strategy-payoff shuffle pairs-strategy-payoff

  let sorted-list sort-by [ [l1 l2] -> last l1 > last l2 ] 
      pairs-strategy-payoff
  set strategy-after-revision (first (first sorted-list))
end

Implementation of to direct-pairwise-difference-rule

To implement this rule, the code of procedure to imitative-pairwise-difference-rule and primitive remove-item can be useful.

Implementation of procedure to direct-pairwise-difference-rule

to direct-pairwise-difference-rule
  let candidate-strategy one-of (remove-item strategy strategy-numbers)

  ;; compute difference in payoffs
  let payoff-diff ((payoff-for-strategy candidate-strategy) - payoff)

  set strategy-after-revision ifelse-value
    (random-float 1 < (payoff-diff / max-payoff-difference))
      [ candidate-strategy ]
      [ strategy ]
    ;; If your strategy is the better, payoff-diff is negative,
    ;; so you are going to stick with it.
    ;; If it's not, you switch with probability
    ;; (payoff-diff / max-payoff-difference)
end

Implementation of to direct-positive-proportional-m-rule

To implement this rule, it is useful to have a look at the code of procedure to direct-best-rule, load the rnd extension, and use primitive rnd:weighted-one-of-list.

Implementation of procedure to direct-positive-proportional-m-rule

to direct-positive-proportional-m-rule
  let pairs-strategy-payoff (map [
    [s] -> list s ((payoff-for-strategy s) ^ m)
  ] strategy-numbers)

  set strategy-after-revision first
      rnd:weighted-one-of-list pairs-strategy-payoff [ [p] -> last p ]
end

To avoid errors when payoffs are negative, we will include procedure to check-payoffs-are-non-negative, just like we did in chapter III-4 and chapter chapter IV-4.

to check-payoffs-are-non-negative
  if min-of-payoff-matrix < 0 [
    user-message (word
      "Since you are using decision-rule =\n"
      "imitative-positive-proportional-m,\n"
      "all elements in the payoff matrix\n"
      payoffs
      "\nshould be non-negative numbers.")
  ]
end

An appropriate place to call this procedure would be at the end of procedure to setup-payoffs, which would then be as follows:

to setup-payoffs
  set payoff-matrix read-from-string payoffs
  set n-of-strategies length payoff-matrix
  set strategy-numbers range n-of-strategies

  ;; new lines below
  set min-of-payoff-matrix min reduce sentence payoff-matrix
  set max-of-payoff-matrix max reduce sentence payoff-matrix
  set max-payoff-difference (max-of-payoff-matrix - min-of-payoff-matrix)

  if decision-rule = "direct-positive-proportional-m"
     [ check-payoffs-are-non-negative ]
end

5.4. Complete code of Extension II in the Code tab

Well done! We have now finished the second extension!

extensions [rnd]

globals [
  payoff-matrix
  n-of-strategies
  n-of-players

  strategy-numbers
  strategy-frequencies
  strategy-expected-payoffs

  min-of-payoff-matrix  ;; <= new global variable
  max-of-payoff-matrix  ;; <= new global variable
  max-payoff-difference ;; <= new global variable
]

breed [players player]

players-own [
  strategy
  strategy-after-revision
  payoff
]

;;;;;;;;;;;;;
;;; SETUP ;;;
;;;;;;;;;;;;;

to setup
  clear-all
  no-display
  setup-payoffs
  setup-players
  setup-graph
  reset-ticks
  update-strategy-expected-payoffs
  update-graph
end

to setup-payoffs
  set payoff-matrix read-from-string payoffs
  set n-of-strategies length payoff-matrix
  set strategy-numbers range n-of-strategies

  ;; new lines below
  set min-of-payoff-matrix min reduce sentence payoff-matrix
  set max-of-payoff-matrix max reduce sentence payoff-matrix
  set max-payoff-difference (max-of-payoff-matrix - min-of-payoff-matrix)

  if decision-rule = "direct-positive-proportional-m"
     [ check-payoffs-are-non-negative ]
end

to setup-players
  let initial-distribution read-from-string n-of-players-for-each-strategy

  if length initial-distribution != length payoff-matrix [
    user-message (word "The number of items in\n"
      "n-of-players-for-each-strategy (i.e. "
      length initial-distribution "):\n"
      n-of-players-for-each-strategy
      "\nshould be equal to the number of rows\n"
      "in the payoff matrix (i.e. "
      length payoff-matrix "):\n"
      payoffs
    )
  ]

  let i 0
  foreach initial-distribution [ j ->
    create-players j [
      set payoff 0
      set strategy i
      set strategy-after-revision strategy
    ]
    set i (i + 1)
  ]

  set n-of-players count players
end

to setup-graph
  set-current-plot "Strategy Distribution"
  foreach (range n-of-strategies) [ i ->
    create-temporary-plot-pen (word i)
    set-plot-pen-mode 1
    set-plot-pen-color 25 + 40 * i
  ]
end

;;;;;;;;;;
;;; GO ;;;
;;;;;;;;;;

to go
  ask players [update-payoff]

  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]

  tick
  update-strategy-expected-payoffs
  update-graph
end

;;;;;;;;;;;;;;;;;;;;;;
;;; UPDATE PAYOFFS ;;;
;;;;;;;;;;;;;;;;;;;;;;

to update-strategy-expected-payoffs
  set strategy-frequencies map [ n ->
        count players with [strategy = n] / n-of-players
      ] strategy-numbers
  set strategy-expected-payoffs map [ list-of-payoffs ->
      sum (map * list-of-payoffs strategy-frequencies) ] payoff-matrix
end

to update-payoff
  run payoff-to-use
end

to play-with-one-rd-agent
  let mate one-of other players
  set payoff item ([strategy] of mate) (item strategy payoff-matrix)
end

to use-strategy-expected-payoff
  set payoff item strategy strategy-expected-payoffs
end

;;;;;;;;;;;;;;;;;;;;;;;;;
;;; UPDATE STRATEGIES ;;;
;;;;;;;;;;;;;;;;;;;;;;;;;

to update-strategy-after-revision
  ifelse random-float 1 < noise
    [ set strategy-after-revision (random n-of-strategies) ]
    [ run (word decision-rule "-rule") ]
end

to update-strategy
  set strategy strategy-after-revision
end

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;; imitative decision rules ;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

to imitate-if-better-rule
  let observed-player one-of other players

  if ([payoff] of observed-player) > payoff [
    set strategy-after-revision ([strategy] of observed-player)
  ]
end

to imitative-pairwise-difference-rule
  let observed-player one-of other players

  ;; compute difference in payoffs
  let payoff-diff ([payoff] of observed-player - payoff)

  set strategy-after-revision ifelse-value
    (random-float 1 < (payoff-diff / max-payoff-difference))
      [ [strategy] of observed-player ]
      [ strategy ]
    ;; If your strategy is the better, payoff-diff is negative,
    ;; so you are going to stick with it.
    ;; If it's not, you switch with probability
    ;; (payoff-diff / max-payoff-difference)
end

to imitative-linear-attraction-rule
  let observed-player one-of players

  set strategy-after-revision ifelse-value
    (random-float 1 <
           ([payoff] of observed-player - min-of-payoff-matrix) /
           ( max-of-payoff-matrix - min-of-payoff-matrix) )
      [ [strategy] of observed-player ]
      [ strategy ]
end

to imitative-linear-dissatisfaction-rule
  let observed-player one-of players

  set strategy-after-revision ifelse-value
    (random-float 1 <
           (max-of-payoff-matrix - payoff) /
           (max-of-payoff-matrix - min-of-payoff-matrix) )
      [ [strategy] of observed-player ]
      [ strategy ]
end

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;; direct decision rules ;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

to-report payoff-for-strategy [s]
  report ifelse-value payoff-to-use = "play-with-one-rd-agent"
    [item ([strategy] of one-of other players) (item s payoff-matrix)]
    [item s strategy-expected-payoffs]
end

to direct-best-rule
  let pairs-strategy-payoff (map [
    [s] -> list s (payoff-for-strategy s)
  ] strategy-numbers)

  ;; the following line ensures that ties
  ;; are resolved (uniformly) at random
  set pairs-strategy-payoff shuffle pairs-strategy-payoff

  let sorted-list sort-by [ [l1 l2] -> last l1 > last l2 ] 
      pairs-strategy-payoff
  set strategy-after-revision (first (first sorted-list))
end

to direct-pairwise-difference-rule
  let candidate-strategy one-of (remove-item strategy strategy-numbers)

  ;; compute difference in payoffs
  let payoff-diff ((payoff-for-strategy candidate-strategy) - payoff)

  set strategy-after-revision ifelse-value
    (random-float 1 < (payoff-diff / max-payoff-difference))
      [ candidate-strategy ]
      [ strategy ]
    ;; If your strategy is the better, payoff-diff is negative,
    ;; so you are going to stick with it.
    ;; If it's not, you switch with probability
    ;; (payoff-diff / max-payoff-difference)
end

to direct-positive-proportional-m-rule
  let pairs-strategy-payoff (map [
    [s] -> list s ((payoff-for-strategy s) ^ m)
  ] strategy-numbers)

  set strategy-after-revision first
      rnd:weighted-one-of-list pairs-strategy-payoff [ [p] -> last p ]
end

;;;;;;;;;;;;;;;;;;;;
;;; UPDATE GRAPH ;;;
;;;;;;;;;;;;;;;;;;;;

to update-graph
  set-current-plot "Strategy Distribution"
  let bar 1
  foreach strategy-numbers [ n ->
    set-current-plot-pen (word n)
    plotxy ticks bar
    set bar (bar - (item n strategy-frequencies))
  ]
  set-plot-y-range 0 1
end

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;; SUPPORTING PROCEDURES ;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

to check-payoffs-are-non-negative
  if min-of-payoff-matrix < 0 [
    user-message (word
      "Since you are using decision-rule =\n"
      "imitative-positive-proportional-m,\n"
      "all elements in the payoff matrix\n"
      payoffs
      "\nshould be non-negative numbers.")
  ]
end

6. Exercises

You can use the following link to download the complete NetLogo model: nxn-games-in-well-mixed-populations.nlogo.

Exercise 1. Implement a decision rule that you can call “imitate-the-best”. This is the imitate the best neighbor rule adapted to well-mixed populations. Under this rule, the revising agent copies the strategy of the individual with the greatest payoff. Resolve ties uniformly at random.

Exercise 2. Implement a decision rule that you can call “imitative-positive-proportional-m“. This is the imitative-positive-proportional-m rule implemented in chapter III-4, adapted to well-mixed populations. Under this decision rule, the revising agent selects one individual at random, with probabilities proportional to payoffs raised to parameter m, and copies her strategy. Please do not allow for negative payoffs when using this rule.

Exercise 3. Implement a decision rule that you can call “imitative-logit-m“. Under this decision rule, the revising agent selects one individual at random, with probabilities proportional to $e^{m \pi_i}$ (where $\pi_i$ denotes agent $i$ ‘s payoff), and copies her strategy.

Exercise 4. Implement a decision rule that you can call “Fermi-m“. This is the Fermi-m rule implemented in chapter III-4, adapted to well-mixed populations. Under this rule, the revising agent $i$ looks at another individual $j$ at random and copies her strategy with probability $\frac{e^{m \pi_j}}{e^{m \pi_i}+e^{m \pi_j}}$ , where $\pi_z$ denotes agent $z$ ‘s payoff and $m\ge0$ .

Exercise 5. Implement a decision rule that you can call “direct-logit-m”. Under this rule, the revising agent selects one strategy at random, with probabilities proportional to $e^{m \pi_i}$ (where $\pi_i$ denotes strategy $i$ ‘s payoff), and adopts it.

Exercise 6. In this model, we run procedure to update-strategy-expected-payoffs at the end of to go, as shown below:

to go
  ask players [update-payoff]

  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]
  tick
 
  update-strategy-expected-payoffs ;; <= current position
  update-graph
end

Since procedure to update-strategy-expected-payoffs updates the expected payoffs, and these are used by agents in procedure to update-payoffs, it may seem more natural to run procedure to update-strategy-expected-payoffs just before asking players to update their payoff, as shown below:

to go
  update-strategy-expected-payoffs ;; <= new position
  ask players [update-payoff]

  ask players [
    if (random-float 1 < prob-revision) [
      update-strategy-after-revision
    ]
  ]
  ask players [update-strategy]
  tick

  update-graph
end

What would change if we did this?

Hint

You may compare the two alternatives in a setting where agents play Rock-Paper-Scissors (as in figure 2), payoff-to-use = “use-strategy-expected-payoff“, prob-revision = 1, noise = 0, and decision-rule = “direct-best“.

In chapter II-4 we were able to implement a more efficient version of this model, but the speed boost came at the expense of making our code less readable. Here we want to focus on code readability, so we start with the most natural implementation of the model, i.e. nxn-imitate-if-better-noise. Nonetheless, we can add the primitive no-display in procedure to setup, right after clear-all, to improve the efficiency of the model at hardly any cost. ↵
There are decision rules that are neither imitative nor direct. See, e.g., Lahkar and Sandholm (2008). ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Agent-Based Evolutionary Game Dynamics Copyright © 2024 by Luis R. Izquierdo, Segismundo S. Izquierdo & William H. Sandholm is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.