Fluoride Ion Electrode
TOC/Help. Click to here expand/hide
Overview
Background
Pre-lab work
Experimental
Post-lab work
![]() For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
Overview
In this experiment, you'll gain hands-on experience constructing a fluoride ion selective electrode-reference electrode pair and study its characteristics. You'll also learn to use this electode system for analytical purposes and explore the method of standard addition for quantitatively evaluating samples with unknown matrices.
Learning Objectives
- Understand how an ion selective electrode (ISE) works and how it is different from other metal electrodes that involve redox processes.
- Learn the key components of ISE.
- Construct a fluoride ISE and learn the standard procedures involved with the use of a fluoride ISE to quantify fluoride.
- Understand why and when to use the Method of Standard Addition.
To cite this lab manual: “Fluoride Ion Selective Electrode”. A Manual of Experiments for Analytical Chemistry. Department of Chemistry at UW- Madison, Summer 2024.
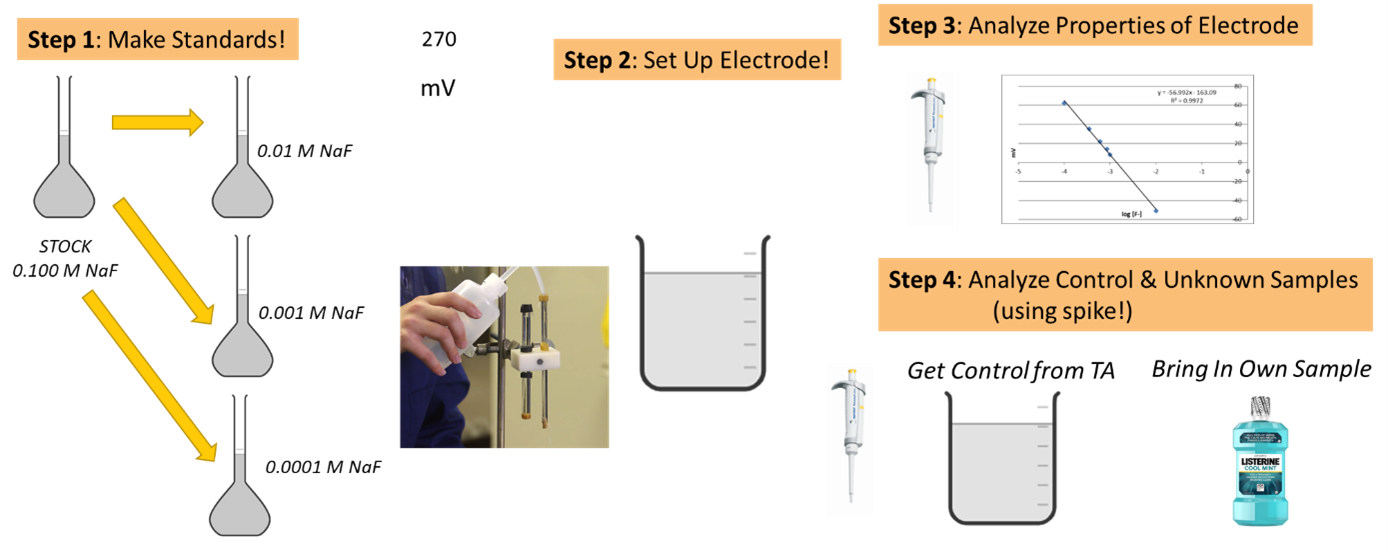
Visual Abstract

Background
Ion selective electrodes (ISEs) are used to determine the concentration or activity of a selected species by relating concentration or activity information to an electrode potential. These measurements are easily made with a voltmeter. However, ISEs are fundamentally different from metal indicator electrodes in that the detection of the selected species by ISEs does not involve the redox processes of the species at the electrode, as explained below. In this lab, we construct a fluoride ISE and quantify the amount of fluoride in the analyte. The measurement set up is composed of an Ag/AgCl reference electrode, a fluoride ISE, and a multimeter.
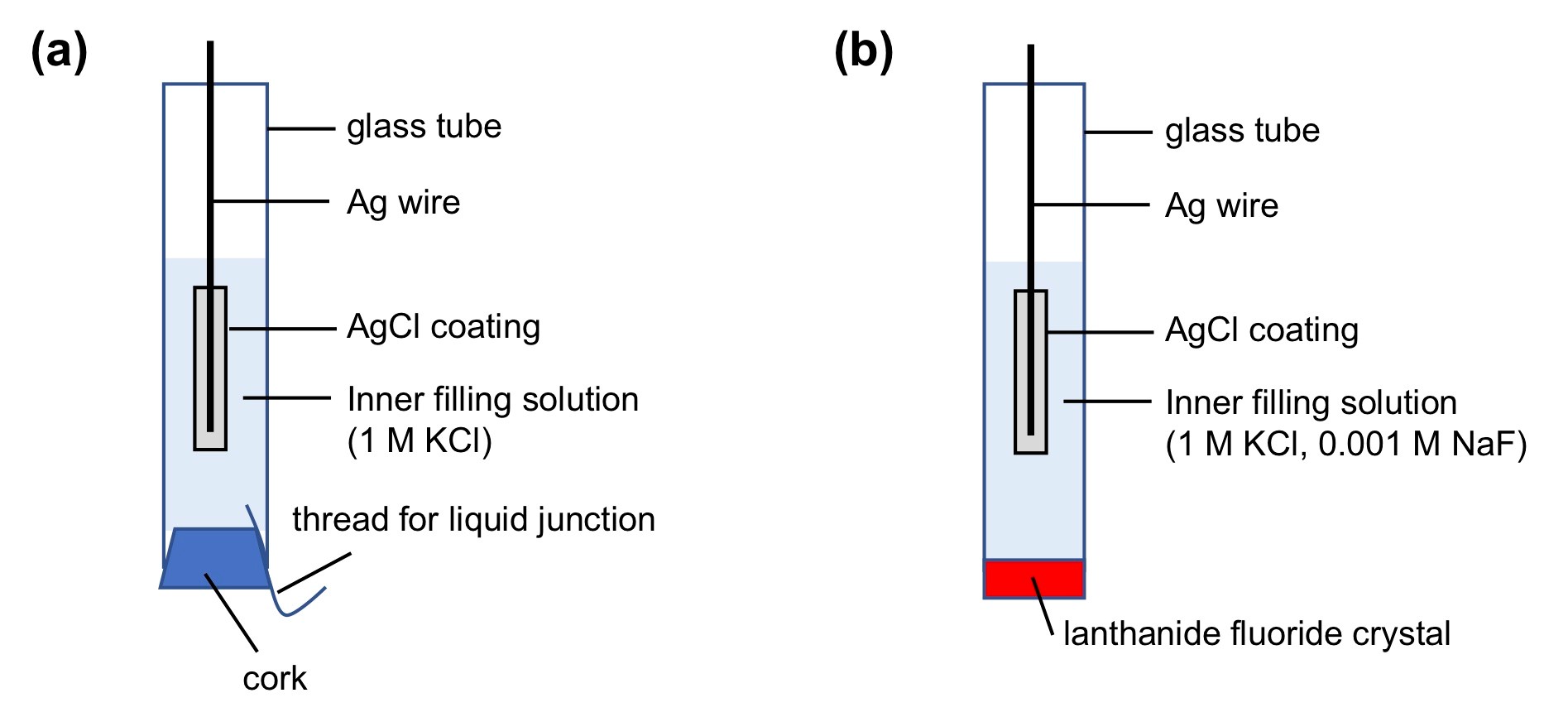
An Ag/AgCl reference electrode that will be used in this experiment is shown in Figure 1a, where an Ag/AgCl electrode is immersed in an inner solution containing a known amount of chloride (1 M KCl).
The redox reaction for this electrode is:
| AgCl(s) + e¯ ⇌ Ag(s) + Cl¯(aq) | (1) |
Since the amount of chloride is known, the potential of this reference electrode is known.
A fluoride ISE can be constructed by making two modifications to the Ag/AgCl reference electrode (Figure 1b). First, the bottom of the Ag/AgCl reference electrode is capped by an ion selective membrane. In this experiment, our ion of interest is fluoride. Thus, a lanthanide fluoride crystal doped with Eu2+, which can selectively bind fluoride ions, is used. Second, we add a known amount of fluoride to the inner solution so that the inner solution contains a known amount of both chloride and fluoride (1 M KCl + 0.001 M NaF).
Then, the Ag/AgCl reference electrode and the fluoride ISE are immersed in a beaker containing an analyte solution whose fluoride concentration needs to be determined, and the potential difference between the Ag/AgCl reference electrode and the fluoride ISE is measured by a multimeter (Figure 2).
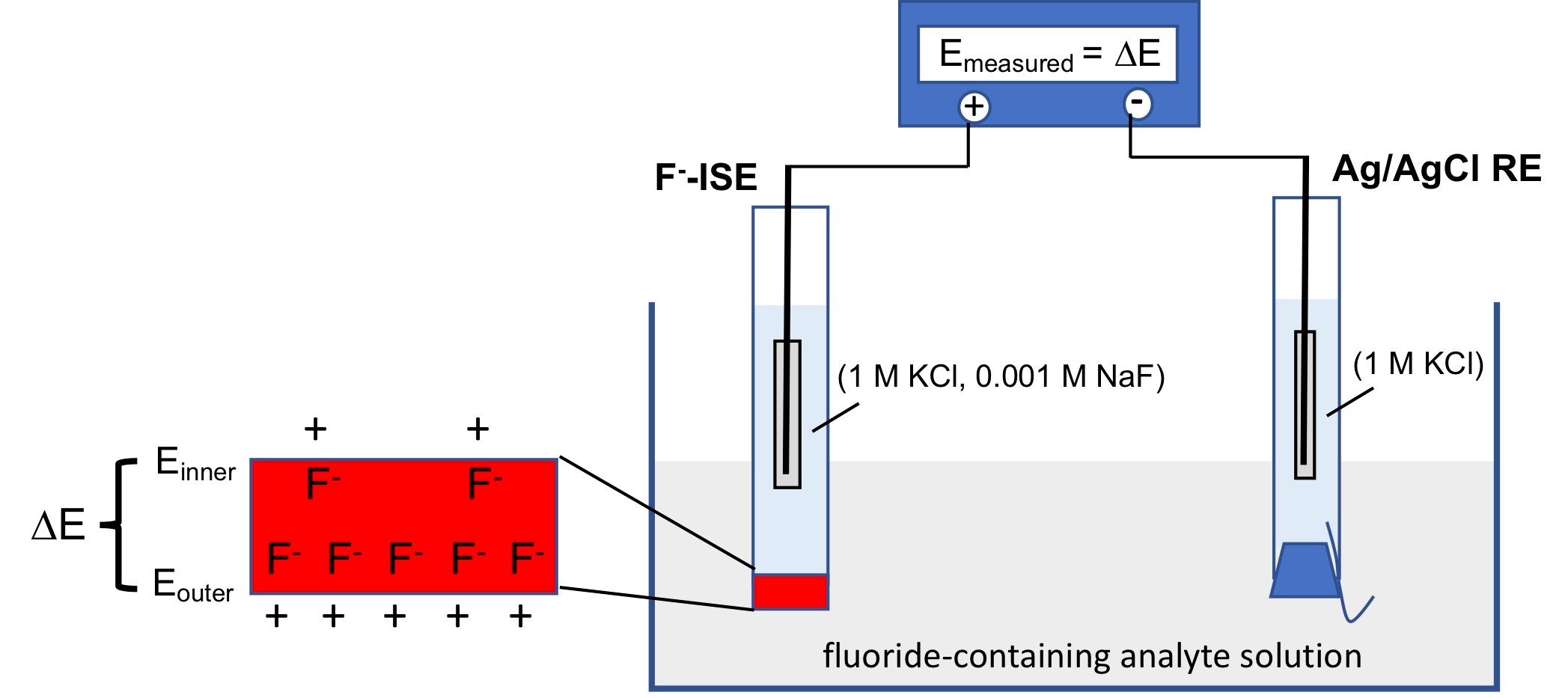
It should be noted that the ISE and the reference electrode use the same Ag/AgCl electrode and their inner solutions contain the same amount of chloride. Thus, the potentials of the two electrodes determined by the redox reaction shown in Equation 1 are the same and the potential difference between these two electrodes must be zero.
However, there is another way to create a potential difference between these two electrodes. Note that one side of the lanthanide fluoride crystal placed at the bottom of the ISE is in contact with the inner solution of the ISE while the other side is in contact with the analyte solution. The amount of fluoride bound to the membrane is proportional to the activity of the fluoride in the solution. Therefore, if these two solutions contain different amounts of fluoride, the amounts of fluoride bound to two sides of the membrane are different. This creates a potential difference across the membrane, which can be measured, by the multimeter, as the potential difference between the reference electrode and the ISE electrode. Since this potential difference is related to the activity difference of the fluoride in the two solutions and the activity of the fluoride in the inner solution is known, the measured potential can be used to determine the activity of the fluoride ion in the analyte. This is how the ISE can quantify the amount of fluoride without involving the redox chemistry of fluoride.
In general, the essential requirements for an ISE are:
- Selective: It will give a response to the concentration of a specific ion and be free of signal from interfering ions. (You need a membrane that binds only a specific ion.)
- Speedy: The response time is fast (e.g., <1 second).
- Sturdy: It should be durable and not easily contaminated by other substances in solution.
- Systematic: It will give reproducible and meaningful results within the normal range of activities (or concentrations).
- Simple: It is easy to construct and use.
The fluoride electrode used in this experiment meets these rather stiff requirements. Another widely used ISE that you have already worked extensively with is a H+ ISE, also known as a pH meter, which measures the activity of H+ in solution. And, you have probably already developed an appreciation for how easy and fast this type of measurement can be compared to other methods of quantitation!
A question to consider: do you know what material is used as a H+-selective membrane in the pH meter?
The Relationship Between AF¯ and the Measured Potential, Emeasured
We begin with the general equation that shows the relationship between Emeasured and the fluoride activity in the analyte solution:
| Emeasured = constant + S∙logAF | (2) |
In this equation, S is used to denote the slope of the line when Emeasured is plotted as a function of logAF. S is determined by the following equation,
| [latex]S = \beta (2.303) \dfrac{RT}{nF}[/latex] | (3) |
where R is the gas constant, T is the temperature in Kelvin, F is Faraday's constant, and n is the charge of the analyte ion ( -1 for the fluoride ion). β depends on the particular ISE. For the fluoride ISE, this value is close to 1.00.
Equation 2 can be rewritten as:
| Emeasured = constant + S∙log(γF[F¯]) | (4) |
| Emeasured = constant + S∙log(γF) + S∙log[F¯] | (5) |
| Emeasured = constant + S∙log[F¯] | (6) |
In the last equation, the log of the activity coefficient has been combined with the other constants in the equation. Because you keep the ionic strength constant when making your measurements, the activity coefficient will be the same for all measurements and it can be lumped with the other constants.
When at least two solutions of known F¯ concentrations are prepared and Emeasured are recorded using a F¯ ISE, the slope (S) and the y-intercept (constant) of the Emeasured – log [F¯] plot (Equation 6) can be determined. Then, this calibration plot can be used to determine the [F¯] in any solution by measuring Emeasured. However, this is true only when the composition (i.e., matrix) of the analyte solution is very similar to the composition of the standard solutions used to construct the Emeasured – log [F¯] plot. If the composition of the analyte solution is complex or very different from that of the standard solutions, the “constant” determined by the calibration plot will be different from the “constant” of the analyte solution. Therefore, [F¯] of the analyte solution cannot be accurately determined. In this case, the method of standard addition must be used, which can determine [F¯] by using S but without knowing the “constant” of the analyte solution.
The Method of Standard Addition
The method of standard addition is discussed in detail in your text and may be covered in the lecture of this course. Briefly, in this quantitative method, a sample that contains an unknown amount of the analyte of interest is first measured. The sample is then spiked with a known concentration of the same analyte and subsequently measured again. Depending on the type of measurement, the response at the detector may be linearly proportional to the concentration of sample, as in a spectrophotometric measurement of absorbance that follows Beer's Law. In a potentiometric measurement like the one in this lab, the detector response (voltage) is linearly proportional to the log of the concentration. The appropriate standard addition equation will depend on this relationship between the detector signal and analyte concentration. Below is the derivation of the equation appropriate for this lab, in which you determine fluoride concentration of a sample using a potentiometric measurement.
To derive the equation for standard addition, we will use the following terms:
- Ei = the measured potential of sample before the addition of standard
- Ef = the measured potential of the sample plus the added standard
- [F¯]i = the concentration of fluoride in sample before addition of standard
- [F¯]f = the concentration of fluoride in sample after the addition of standard
Using Equation 6, we can write an expressions for both Ei and Ef:
| Emeasured = constant + S∙log[F¯]i | (7) |
| Emeasured = constant + S∙log[F¯]f | (8) |
Subtracting Equation 7 from Equation 8 yields:
| Ef - Ei = (constant + S∙log[F¯]f) - (constant + S∙log[F¯]i) | (9) |
The constants cancel because they are the same in both equations. Using ∆E = Ef - Ei and combining the log terms gives:
| [latex]\Delta E = S \cdot \log \dfrac{[F^-]_f}{[F^-]_i}[/latex] | (10) |
Taking the antilog of both sides yields:
| [latex]\text{antilog}\left( \dfrac{\Delta E}{S} \right) = \dfrac{[F^-]_f}{[F^-]_i}[/latex] | (11) |
[F¯]f can be written as:
| [latex][F^-]_i \cdot \dfrac{V_i}{V_f} + \Delta C[/latex] | (12) |
Where ∆C is the change in concentration of analyte in the solution due to the addition of the standard. The initial volume is Vi, while the final volume after standard addition is represented by Vf. Substituting this expression into Equation 11 and doing some algebra yields:
| [latex]\text{antilog} \left( \dfrac{\Delta E}{S} \right) = \dfrac{[F^-]_i \cdot \frac{V_i}{V_f} + \Delta C }{[F^-]_i} = \dfrac{V_i}{V_f} + \dfrac{\Delta C}{[F^-]_i}[/latex] | (13) |
Finally, solving for [F¯]i yields:
| [latex][F^-]_i = \dfrac{\Delta C}{\text{antilog} \left( \frac{\Delta E}{S} \right) - \frac{V_i}{V_f}}[/latex] | (14) |
It is important to note here that additional volume added to your sample using this method MAY impact the concentrations you calculate. This volume change is accounted for specifically in Equation 14. If the volume added to your sample is insignificant compared to the sample size, the term [latex]\frac{V_i}{V_f}[/latex] can be simplified to equal 1. In deciding whether you can make this simplification or not, you must consider the significant figures you expect to achieve in your final answer and decide if the change in volume will negatively and systematically influence your answer based on the approximation. In this lab, you should expect to report answers accurately to ± 0.0005 M.

Lab Concept Video
click here to hide the video (for printing purpose).
Write down your observations or notes from the video in your lab notebook.
Pre-lab Work

Lab Skills
Review these lab skills videos prior to lab.
click here to hide the video playlist (for printing purpose).
Key Takeaways
- Accurately determining the concentration of fluoride requires using volumetric glassware appropriately.
Extra Resources:

Prelaboratory Exercises
- Work out with your lab partner who will bring in a fluorinated sample from home to analyze. Products could include toothpaste, mouthwash, bottled water fortified with fluoride, etc.; check the product ingredients to make sure a measurable amount is listed on the packaging. Describe in your notebook your final choice and specifically log the concentration of fluoride as it is described on the packaging.
- Manufacturers of toothpaste, mouthwash, and other products designed to provide the user with safe exposure to fluoride must report concentrations on their labels. Most often, these concentrations are provided in units of weight percent (remember the % KHP lab?) or weight (g) per volume (mL) percent. BEFORE COMING TO LAB, calculate how much product you will measure out and dilute (be sure to use total ionic strength adjusting buffer (TISAB; see procedure) and assume you will follow roughly the procedure provided) so that the final concentration of the sample in your beaker is on the order of ~0.003 M F¯. Pay special attention to the unit convention on the packaging of the product and convert the units accordingly. Write in your notebook a preliminary procedure for preparing the sample you chose above for analysis.
- NaF (MW 41.99 g/mol) is hygroscopic and, when used as a primary standard, should be dried in an oven at 110 °C for 1-2 hours. Your instructor will either dry the solid material for you or instruct you to dry about 3 grams of the solid a lab period before. During the lab, you will need to prepare a stock solution of 0.100 M NaF. Calculate the amount of needed to prepare 500 mL of this standard stock solution.

Before You Take The Quiz on Canvas
- Understand how an ion selective electrode produces an electric potential related to the concentration of a particular ion in a solution.
- Understand the method of standard addition and how it is used in this experiment.
- Be able to calculate the concentration of fluoride in an unknown using standard addition given a set of raw data—the electrode slope, the measured potential of the prepared unknown, and the measured potential of the prepared unknown spiked with a known concentration of fluoride.

Experimental
- Preparation of stock solutions.
- Stock 0.100 M NaF. Dry approximately 3 grams of sodium fluoride at 110 °C for 1-2 hours. Allow to cool in your desiccator. Accurately weigh the appropriate amount of dry NaF (see prelaboratory exercise 3). Quantitatively transfer to a 500 mL volumetric flask. Dissolve in water and dilute to mark.
- Total Ionic Strength Adjusting Buffer (TISAB). This solution has been prepared for you. (TISAB is prepared by dissolving 58.44 g NaCl, 42 mL of 6 M acetic acid, 102 g of sodium acetate and 0.3 g of sodium citrate in water and diluting to 1000 mL.) The total ionic strength of a sample affects the activity coefficient, which impacts the measurement made by the ion selective electrode. For this reason, it is VERY important to hold the ionic strength constant for all standards and samples. Minimizing variations in ionic strength between samples will minimize potential for error. Note its use in the procedure below.
- Electrode preparation. Obtain a fluoride ion electrode assembly from the stockroom. Prepare the electrodes as follows:
- Prepare two silver wires lightly coated with silver chloride by electrolyzing in 1 M HCl for a few seconds.
- Prepare the ISE electrode. Fill the tube holding the LaF3 crystal (Figure 1) with fluoride filling solution (1 M KCl, 0.001 M NaF). Insert one silver chloride coated silver wire into the filling solution (Figure 1).
- Prepare the reference electrode. To assemble the cell (shown in Figure 2), insert the thread, wet the cork with filling solution, and insert the cork over the thread into the end of the glass tube. Add filling solution (1 M KCl) to the tube, insert the second lightly coated silver wire, and rinse the outside of the tube with deionized water.
- Creation of test solutions. Prepare the following set of solutions in 100 mL volumetric flasks:
- 0.01 M F‾: Pipet 10 mL of STOCK 0.1 M NaF. 50 mL of TISAB, and dilute to the mark with water.
- 0.001 M F¯: Pipet 1 mL of STOCK 0.1 M NaF, 50 mL of TISAB, and dilute to the mark with water.
- 0.0001 M F¯: Pipet 1 mL of 0.01 M F¯ solution (first solution above), 50 mL of TISAB, and dilute to the mark with water.
- Study of electrode properties. Use a voltmeter in the absolute millivolt mode to make these measurements.
- Connect the electrodes to the voltmeter. The reference electrode should be connected to the negative terminal. The ISE should be connected to the positive terminal. Rinse both electrodes with deionized water. Blot off electrodes with tissue.
- Pour all of the 0.0001 M F¯ solution into a 150 mL beaker. When carrying out selective ion measurements, it is important to have good agitation. This allows a fresh supply of ions to be exposed to the sensing portion of the ISE. Set the beaker on a stir plate, and add your stir bar to the solution. Select a speed that keeps a constant, smooth motion. Avoid stirring at a turbulent rate. Immerse the electrodes in this solution. Make sure the stir bar is not hitting the electrode. Measure the cell potential. Note the time required to reach a steady potential reading.
- Using a micropipet, add 250 μL of STOCK 0.1 M NaF to the solution in the beaker. Measure the cell potential of the resulting solution. Add a second 250 μL portion of STOCK 0.1 M NaF to the solution and measure the cell potential. Repeat with a third portion of STOCK NaF solution.
- Now measure the potentials of the 0.001 M F¯ and 0.01 M F¯ test solutions.
- Determine the electrode slope, S, from a plot of Emeasured vs. log[F¯].
- Analysis the Control Sample. Obtain a sample of fluorinated water of known concentration to be used as a control from your laboratory instructor. Determination of control fluoride concentration by method of standard addition.
- Into a 100 mL volumetric flask, pipet 50 mL of the Control Sample. Dilute to the mark with TISAB.
- Pour all of the solution into a 150 mL beaker. Determine the cell potential of this solution using the same procedure as you used for the test solutions.
- Pipet 1 mL of STOCK 0.1 M F¯ into the solution in the cell. Mix well. Measure the cell potential.
- Calculate the fluoride ion concentration and verify the accuracy of your answer with your instructor.
- Analysis of Personal Fluorinated Sample. Now that you are familiar with the set-up, operation, and calculations related to the fluoride ISE, it is time for you to develop your own procedure with the purpose of validating the product contents of a sample of your choice. Here are some guidelines for you to consider:
- It is important that you use a freshly calibrated electrode for collecting the data. If for some reason you are repeating this portion of the experiment or doing it on a different day than when you did parts 1-5, you should freshly calibrate the electrode using the procedure outlined above.
- Verify with a positive control that the electrode apparatus is reliable.
- Prepare your sample according to the procedure you described in the prelaboratory exercises. Be sure to use TISAB when preparing the sample. Measure your sample for fluoride and immediately verify whether your answer is in line with the product content specifications. It is likely you will need to make some adjustments to your sample preparation procedure. Most important is that the mV measured on the meter is WITHIN the calibrated range of the electrode. If its outside the calibrated range, then you will need to rethink how you worked through the prelaboratory exercise. Perhaps a simple dilution is all that’s needed. But perhaps initially there was a calculation error. You will need to find it and fix it.
- If you have time, verify your measurement with a second or third preparation and measurement of the sample. A good analytical measurement will be reported with an average and a standard deviation, which requires multiple measurements!
Post-Lab Work Up

Results/Calculations
Fill out the answer sheet for this experiment completely. Answer the following post-lab questions.
- As described in the procedure above, construct a plot of Emeasured vs. log[F¯]. Make sure all axes are labeled and the graph is titled.
- In a short paragraph, describe the procedure you developed to prepare the unknown sample. Briefly describe any modifications or adjustments you had to make to your sample preparation. Especially if you simply couldn’t get the experiment to work, describe here the problems you had and what you did to try and fix them.
- Write a short reflective summary. Compare your measured results with the manufacturer label. How much do you trust your measurement?

Challenge Questions
Challenge questions are designed to make you think deeper about the concepts you learned in this lab. There may be multiple answers to these questions. Any honest effort at answering the questions will be rewarded.
- Determine the [F¯] of the control sample (Experimental Step 5) by using the Emeasured of the control sample and the calibration curve (a plot of Emeasured vs. log[F¯] constructed by using standard solutions) obtained from Experimental Step 4 (i.e., using the calibration curve). Compare [F¯] obtained from this method to the [F¯] obtained with standard addition (Experimental Step 5). Are they similar? Did you expect them to be similar or different? Why?
- Determine the [F¯] of your sample used for Experimental Step 6 by using the Emeasured of your sample and the calibration curve obtained from Experimental Step 4. Compare [F¯] obtained from this method to the [F¯] obtained using Standard Addition (Experimental Step 6). Are they similar? Did you expect them to be similar or different? Why?
- When spiking a sample to perform standard addition, the volume of the solution of known [F¯] added to the unknown sample is always very small. Can you explain why? Wouldn’t it be more reliable if we add a larger volume of the known [F¯] solution? Why don’t we?

Lab Report Submission Details
Submit your lab report on Canvas as 1 combined PDF file. This submission should include:
- The completed answer sheet.
- Your lab notebook pages associated with this lab, which should include answers to the post-lab questions and challenge questions.
The grading rubric can be found on Canvas.
- Shatkay, A., Anal. Chem. 39, 1056 (1967).
- Frank, M. S. and Ross, J. W., Jr., Anal. Chem. 40, 1169 (1968).
- Moody, G. J. and Thomas, J. D. R., Selective Ion Sensitive Electrodes, Merrow:Herts, 1971.
- Laitinen, H. A. and Harris, W. E., Chemical Analysis, McGraw-Hill, New York, 1960.
- Harris, D. C. & Lucy, C. A. Quantitative Chemical Analysis, 10th ed.; W. H. Freeman: New York, NY, 2020
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please ask your instructor or TA.)
