Silver Electrode Study of Equilibria
TOC/Help. Click to here expand/hide
Overview
Background
Pre-lab work
Experimental
Post-lab work
![]() For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
For help before or during the lab, contact your instructors and TAs (detailed contact information are found on Canvas).
Overview
In this experiment we introduce you to concepts and basic principles regarding the use of electrochemistry to probe a chemical system.
Learning Objectives
- Construct and use an electrochemical measurement setup to quantify the concentration or activity of a species of interest in solution. In this study, silver ion is used as a model species of interest.
- Use the activity of the silver ion to determine the equilibrium constants governing the chemistry of silver ions in aqueous solution.
To cite this lab manual: “Silver Electrode Study of Equilibria”. A Manual of Experiments for Analytical Chemistry. Department of Chemistry at UW- Madison, Summer 2024.
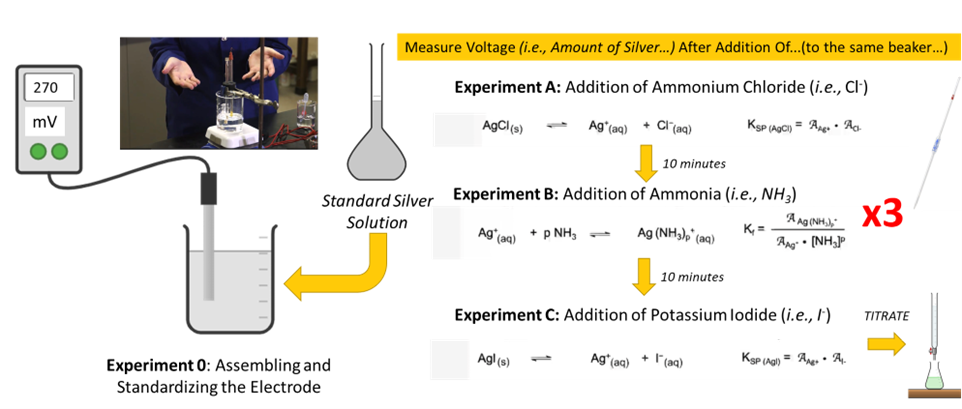
Visual Abstract

Background
An important branch of analytical chemistry is dedicated to using electrochemical means to analytically measure chemical processes. Recall from your general chemistry class that a redox reaction involves the transfer of electrons between reacting species. A chemical is considered oxidized when it loses electrons. It is reduced when electrons are gained. Analytical chemists have cleverly found ways to probe these reactions quantitatively using what they know about electrochemistry and materials chemistry. A more detailed discussion of these fundamentals will be addressed in lecture or can be found in your textbook.
In this experiment we will measure the activity (i.e., effective concentration) of Ag+ (AAg+) in various chemical systems using the following redox reaction:
| Ag+ + e¯ ⇌ Ag E°Ag+ = 799 mV vs. SHE | (1) |
The standard reduction potential of this half-cell reaction is obtained when a silver metal electrode (called an indicator electrode) is immersed in a solution containing Ag+ in its standard state (AAg+ = 1 M) and the potential of the silver metal electrode is measured against the standard hydrogen electrode (SHE) as the reference electrode. When AAg+ is not 1, the reduction potential of this half cell reaction changes as a function of AAg+ as shown in the Nernst equation below:
| [latex]E_{Ag^+} = E^{\circ}_{Ag^+} – N \log \left( \dfrac{1}{\mathcal{A}_{Ag^+}}\right) = E^{\circ} – N \log \left( \dfrac{1}{\gamma [Ag^{+}]} \right)[/latex] | (2) |
where [latex]N = 2.303 \frac{RT}{nF}[/latex] (R = 8.314 J/mol·K, T = temperature in K, n = number of electrons transferred in the reaction, and F = 96485 C/mol). Since n = 1 for Ag+ reduction, if T is assumed to be 298 K, N is a constant of 59.2 mV. Thus, using Eq. 2, you can determine AAg+ in any solution of an unknown amount of Ag+.
In this experiment, the potential of the silver indicator electrode will be measured not against the SHE but against a home made reference electrode. The indicator electrode will be connected as a cathode to the multimeter, and the reference electrode will be connected as an anode to the multimeter. The potential read by the multimeter is determined as follows:
| Emeasured = Ecathode - Eanode + Ejunc | |
| Emeasured = EAg+ - EREF + Ejunc | |
| Emeasured = E°Ag+ – N*log (1/γ[Ag+]) – EREF + Ejunc | (3) |
where EREF is the reduction potential of the half-cell reaction used in a reference electrode and Ejunc is a liquid junction potential, which is a voltage difference developed at the interface of two dissimilar electrolyte solutions in contact. (A more detailed explanation of Ejunc can be found in your textbook.)
Since E°Ag+, EREF, and Ejunc are constant regardless of [Ag+], Eq (3) can be expressed as following:
| Emeasured = k – N*log (1/γ[Ag+]) | (4) |
| k = E°Ag+ - EREF + Ejunc | (5) |
k is called a cell constant and can easily be determined experimentally by measuring Emeasured in a solution of a known AAg+ (this process is called standardizing). Once k is determined, AAg+ in any solution can be accurately quantified by Emeasured using Eq. 4 even without knowing Ejunc or EREF. This is convenient because Ejunc cannot be easily measured or calculated and can become a source of error in accurately determining AAg+ using Emeasured.
Eq. 4 can be rearranged as following:
| [latex]\mathcal{A}_{Ag^+} = \gamma_{Ag^+} [Ag^+] = 10^{^{\left(\frac{E_{measured} - k}{N}\right)}}[/latex] | (6) |
Note that when the laboratory temperature is not 298 K, N is no longer 59.2 mV and needs to be re-calculated using the following equation, where T is the actual laboratory temperature in °C.
| [latex]N = 59.2 \dfrac{273 + T(^{\circ} C)}{298}[/latex] | (7) |
In this experiment, you will determine AAg+ to explore three equilibria:
- Solubility product for silver chloride:
AgCl(s) ⇌ Ag+ + Cl¯ KspAgCl = AAg+·ACl¯ (8) - Formation constant for the silver ammine complex:
Ag+ + pNH3 ⇌ Ag(NH3)p+ Kf = [latex]\dfrac{\mathcal{A}_{Ag(NH_3)_p^+}}{\mathcal{A}_{Ag^+} \cdot [NH_3]^p}[/latex] (9) where p will be experimentally determined.
- Solubility product for silver iodide:
AgI(s) ⇌ Ag+ + I¯ KspAgI = AAg+·AI¯ (10)
You will first complete the standardizing process, where a standard solution of a known [Ag+] will be prepared and AAg+ will be calculated using γ = 0.90 (Under the conditions described in the experimental section, the ionic strength is set at 0.010 and γAg+ is calculated to be 0.90 using the Davies equation). Using this solution, you will measure Emeasured to determine k. You will also measure T to obtain N (Eq. 7). By inserting k and N values to Eq. 6, you will be ready to determine AAg+ in any solution using your experimental setup.
In experiment A, a known and excess quantity of ammonium chloride will be added to the solution used for the standardizing process, resulting in the precipitation of AgCl. With Cl¯ present in excess, we can assume the equilibrium expressed in Eq. 8 goes to completion in favor of forming AgCl. Since you know the amounts of Cl¯ and Ag+ (in mmol) combined, you can easily calculate how many mmols of free Cl¯ remain unreacted in solution. Then, by considering the final volume of the solution, you can calculate [Cl¯] and, therefore, ACl¯. (The activity coefficient for Cl¯ is also 0.90. Think about why.) When the reaction really goes to completion, there should be no Ag+ remaining in solution. However, according to the equilibrium and Ksp shown in Eq 8, a very small amount of Ag+ must remain in solution. (If there were really no Ag+ remaining in solution, Ksp would be zero!) The AAg+ can be accurately determined by the Ag electrode and you will use ACl¯ and AAg+ to calculate KspAgCl using Eq. 8.
In experiment B, a known and excess amount of ammonia will be added to the final solution obtained from experiment A. When ammonia is added, the silver chloride precipitated in experiment A will dissolve to form a thermodynamically more stable silver ammonia complex, Ag(NH3)p+. We will assume that all Ag+ in solution will participate in this reaction and the reaction will go to completion. Since you know the amounts of NH3 and Ag+ (in mmol) present in the reaction mixture, you can calculate how many mmols of Ag(NH3)p+ should form and how many mmols of NH3 should remain in solution if p is known. (The procedure to determine p will be described in the experimental section). Then considering the final volume of the reaction mixture, Ag(NH3)p+ and [NH3] can be calculated. We note that NH3 is volatile and the calculated [NH3] can be different from the real [NH3] of the solution. Therefore, you will experimentally determine [NH3] using acid-base titration. Then, by measuring AAg+ electrochemically and using ANH3 and AAg(NH3)p, you can calculate Kf shown in Eq. 9. Note that γ for neutral NH3 is zero and γ for Ag(NH3)p+ and Ag+ are the same.
In experiment C, a known and excess amount of I¯ will be added to the final solution obtained from experiment B. When I¯ is added, Ag(NH3)p+ will be converted to form thermodynamically more stable silver iodide. Again, we assume that all Ag+ ions in the solution participate in this reaction and the reaction will go to completion. Since you know the mmols of I¯ and Ag+ present in the reaction mixture and the final volume of the reaction mixture, you can calculate remaining [I¯] and AI¯. Thus, by measuring AAg+ electrochemically, you can calculate KspAgI shown in Eq. 10.

Lab Concept Video
click here to hide the video (for printing purpose).
Write down your observations or notes from the video in your lab notebook.
Pre-lab Work

Lab Skills
Review these lab skills videos prior to lab.
click here to hide the video playlist (for printing purpose).
Key Takeaways
- Accurately determining the K-values of each reaction requires using volumetric glassware appropriately.
Extra Resources:

Prelaboratory Exercises
- In your laboratory notebook, sketch a line notation describing each half cell as well as the system under investigation for this experiment. If you need help with what a line diagram should look like, try checking your textbook.
- The preparation of solution used for the standardizing process is described in detail in part 1, Collecting Experimental Data, under the Experimental section. Calculate the AAg+ (not the [Ag+]) of this solution.
- What are the total mmoles of Ag+ available to participate chemically in solution? Does this number change as you continue to add chemicals that react with the Ag+?
- After the standardization, a solution containing excess Cl¯ will be added to the standardizing solution to induce the precipitation of AgCl. Assuming all Ag+ will form AgCl, calculate the mmols of Cl¯ remaining in solution. This can be obtained by subtracting your answer in 3 from total mmoles of Cl¯ added. Then, by dividing it by the total volume, calculate [Cl¯].
- Write the expression describing the activity of Cl‾ in solution. (For Ksp calculation, you need activities and not molarities!)

Before You Take The Quiz on Canvas
- Understand how the measured cell potential relates to the activity of Ag+ in solution..
- Be able to calculate the equilibrium concentration of each ligand in the solution after every addition.
- Be able to calculate the concentration of the stock solution of ammonia from a set of titration data.
- Be able to calculate the cell constant, k, from an initial cell potential and temperature of the solution.
- Be able to calculate equilibrium constants from a set of experimental data.

Experimental
Obtain silver reference and indicator electrode apparatus from the stockroom and set up as follows:
- Preparation of reference electrode: Any reference electrode may be used in this experiment, but commercial saturated calomel electrodes, as used with pH meters, leak significant amounts of chloride and would have to be isolated from the solution under study by using a salt bridge. The design shown below is easy to make and is reliable.
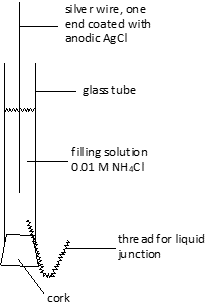
- First, lightly clean off the wire using a plastic scrub pad. Then, coat lightly with silver chloride by making it the anode in a 1 M HCl solution. The cathode in this cell is a copper wire. A battery or power supply is used to pass a current of about 50 milliamperes for about a minute. Hydrogen will be evolved at the cathode, while the silver wire will darken as the coat of AgCl accumulates.
- Insert the thread, wet the cork with the filling solution, and insert it over the thread into the end of the glass tube. Add filling solution (0.01 M NH4Cl) to the tube, insert the silver/silver chloride electrode, and rinse the outside of the tube with distilled water. It is then ready for use.
- Prepare the silver indicator electrode: A length of silver wire (uncoated) serves as the indicator electrode. Clean the electrode surface again with the plastic scrub pad. In this experiment the silver wire has been cemented into the end of a piece of glass tubing.
- Mount the electrodes in their holder in a clamp, so that they may be lowered into a 250 mL beaker. The beaker is placed on a magnetic stirrer (add a stir bar to your solution) so that mixing will be rapid and thorough as the various solutions are added in the experiment.
- You will use a simple multimeter to collect experimental data. At the beginning of the experiment, it is the silver indicator electrode which will have the positive polarity. Connect the red wire with a BNC connector to the silver electrode (this is your working electrode); connect the black wire with the banana plug connector to the reference electrode. Attach the wires to the multimeter. The initial potential should be positive. If you see a negative potential, you literally have your wires crossed! Verify with your TA that you have done the set-up correctly.
Collecting Experimental Data (Note it is appropriate to log experimental observations such as color changes, formation of precipitate, or evolution of a gas as you proceed, along with carefully reading the MV meter)
- Standardizing Process. Into a 100 mL volumetric flask pipet 10 mL of the stock solution which contains 0.001000 M silver nitrate and 0.1000 M ammonium nitrate. Dilute to the mark and mix thoroughly. If there is any cloudiness at this point, your flask is not clean and you must start over. Pour "all" of this solution into the silver electrode compartment, which is the 250 mL beaker you will submerge the electrode apparatus into. Volumetric flasks will not deliver their nominal volume, because of incomplete drainage, but this error will not be serious and you may assume that 100 mL was delivered. Determine the temperature of the solution, and use the corresponding value of the Nernst constant (N) in your calculations.
- Measure the cell voltage with the millivoltmeter, reading carefully to the nearest millivolt. Check this reading with the instructor before proceeding.
- Effect of Addition of Chloride Ion. With the magnetic stirrer working, pipet 10 mL of 0.0100 M ammonium chloride into the cell. Note the formation of a precipitate and the immediate drop in cell voltage. Wait about 10 minutes for the precipitation to reach equilibrium and for the freshly-formed colloidal precipitate to "age" a little. Then read the cell potential to the nearest millivolt.
- Effect of Addition of Ammonia. Pipet 10 mL of the stock solution which contains ammonia and 0.0100 M ammonium nitrate. Note that the silver chloride redissolves and that the potential drops still further, and read it to the nearest millivolt. The silver ammonia complex is more stable than silver chloride. The variable, p, is the coordination number for the complex, to be calculated from your data. Make two more 10 mL additions of the NH3 solution and record the potentials.
- Effect of Addition of Iodide Ion. Pipet 10 mL of 0.0100 M potassium iodide solution into the cell. Note the formation of a precipitate of silver iodide, and describe its color compared to that of silver chloride. Wait about 10 minutes for equilibrium and aging before measuring the potential. If the potential is still drifting appreciably, wait a few minutes longer.
Carefully remove the electrodes from the solution. DO NOT DILUTE OR DISCARD. Leave the beaker and solution in place on the magnetic stirrer. Immediately proceed to the next section. - Determination of the Ammonia Concentration. One source of error in this experiment is the loss of ammonia gas from the cell solution while it is being stirred in contact with the atmosphere. Instead of using whatever molarity may be found for the original stock solution of ammonia it is better to titrate the final cell solution to find the actual concentration present at the end of the measurements.
- Fill a buret with standardized (note precise molarity) 0.5 M hydrochloric acid, which is provided. To the final cell solution add a few drops of bromocresol green indicator solution, which will be blue in the ammonia solution. With the magnetic stirrer running, titrate the solution with the hydrochloric acid until the color changes to green. Slight overtitration will complete the color change to yellow and, although this will not be serious it is best to take the endpoint reading at the green stage.
- Since the experiment involved the addition of three 10 mL portions of the ammonia solution, its effective molarity is now readily calculated:
[latex][NH_3]_{stock} = \dfrac{(V_{HCl\;at\;endpoint})(M_{HCl})}{30}[/latex] (11) - The titration reaction is simply the 1:1 proton transfer:
H+ + NH3 ⇌ NH4+ (12)
Post-Lab Work Up

Results/Calculations
Fill out the answer sheet for this experiment completely. Answer the following post-lab questions.
- Standardizing Process. Calculate k by rearranging Eq. 4 and using Emeasured and the AAg+ of the solution used for the standardizing process, which was determined in the prelaboratory exercises.
- Solubility Product for Silver Chloride. When the ammonium chloride was added, the chloride ion was in considerable excess over the silver ions present, and you may assume that precipitation was virtually complete. Calculate the KSP (see Eq. 8) for AgCl, using AAg+ determined from Emeasured and Eq. 6, and the information calculated in the prelaboratory exercises that estimates the excess (free) Cl¯ in solution.
- Formula and Formation Constant of the Silver-Ammonium Complex. Eq. 9 describes the equilibrium and formation constant expression for the silver-ammonium complex. You may note that the activity coefficients for Ag+ and Ag(NH3)p+ cancel in the equilibrium expression, but since Eq. 6 gives us an easy way to come up with AAg+, you may choose continue to use Eq. 6 for the silver determination and therefore will need to include the activity coefficient for Ag(NH3)p+ in your calculations. The molarity of the complex can be calculated simply by taking account of the dilution of the cell solution, assuming once again that all the silver is converted to the complex ion:
[latex][Ag(NH_3)_p^+] = \dfrac{mmoles\;Ag^+\;total}{total\;volume}[/latex] (13) The equilibrium molarity of ammonia may be calculated simply by considering dilution of the concentrated stock solution,
[latex][NH_3] = \dfrac{(Vol\;of\;NH_3\;added)(Molarity\;of\;NH_3)}{total\;volume}[/latex] (14) assuming that the small amount used to form the silver complex is negligible. You should justify this assumption by a later calculation, once you have determined the value of p.
However, the formation constant cannot be calculated directly because p is as yet unknown. First it is necessary to determine p by making a plot. The expression for Kf rearranged and put into logarithmic form:[latex]\log \dfrac{\mathcal{A}_{Ag(NH_3)_p^+}}{\mathcal{A}_{Ag^+}} = \log K_f + p \cdot \log [NH_3][/latex] (15) Let [latex]Y = \log \dfrac{\mathcal{A}_{Ag(NH_3)_p^+}}{\mathcal{A}_{Ag^+}}[/latex].
A plot of Y versus log[NH3] should be linear, with a slope of p and an intercept of log Kf. Make such a plot with your three data points and determine the value of p from the slope. The formula for the complex is thus deduced, by rounding the experimental value of p to the nearest integer.
Although the plot just described is capable in principle of yielding the value of Kf from its intercept, the extrapolation is rather long and the accuracy of Kf obtained is compromised since it is sensitive to errors in the data points. It is better to assume that the value of p is the integer obtained by rounding, and then to calculate individual Kf values for the three data points. Average the three Kf values and find the standard deviation, which is a measure of the precision of your work. Compare your result with that found in the text or other sources. - Solubility Product for Silver Iodide. This calculation is identical in principle with the method used for silver chloride. Calculate the solubility product and compare with the literature value.
- Calculation of Other Standard Potentials. Use the accepted value for the standard potential for the silver ion/silver couple (E°Ag+ = +0.799 volt), and your determined equilibrium constants to calculate the E° values for the following half‑reactions:
For AgCl(s) + e¯ ⇌ Ag(s) + Cl¯,
E° = E°Ag+ + N∙log(Ksp-AgCl)For Ag(NH3)p+ + e¯ ⇌ Ag(s) + p NH3,
E° = E°Ag+ - N∙log(Kf )For AgI(s) + e¯ ⇌ Ag(s) + I¯,
E° = E°Ag+ + N∙log(Ksp-AgI)

Challenge Questions
Challenge questions are designed to make you think deeper about the concepts you learned in this lab. There may be multiple answers to these questions. Any honest effort at answering the questions will be rewarded.
- Imagine that after the standardizing process, 10 mL of 0.0100 M ammonium chloride is added first to the Ag+ containing solution to form AgCl and then 10 mL of 0.0100 M potassium iodide solution is added to form AgI. Do you think AgI will form in addition to the existing AgCl or do you think the formation of AgI will accompany the dissolution of AgCl? Explain your answer.
- This time, imagine that 10 mL of 0.0100 M potassium iodide is added first to form AgI and then 10 mL of 0.0100 M ammonium chloride is added.
- Would AgCl form?
- Would AAg+ and ACl‾ in this solution satisfy AAg+ × ACl‾ = Ksp AgCl? If yes, why? If not, why not?
- This time, imagine that 10 mL of 0.0100 M ammonium chloride and 10 mL of 0.0100 M potassium iodide are added simultaneously to the Ag+ containing solution.
- Would AgCl and/or AgI form?
- Would the amounts of AgCl and AgI present in this solution be different from those of the final solutions obtained from experiment 1 and 2?
- Would Emeasured in this solution be different from those of the final solutions obtained from experiment 1 and 2?
- Consider reactions (i-iii) shown below. Reaction (iii) is obtained when reaction (i) and reaction (ii) are added together. We know E° for reaction (i) and Ksp for reaction (ii). Thus, in this case, it is possible to determine E° for reaction (iii) by using E° for reaction (i) and Ksp for reaction (ii).
Ag+ + e¯ ⇌ Ag(s) (i) AgCl(s) ⇌ Ag+ + Cl¯ (ii) AgCl(s) + e¯ ⇌ Ag(s) + Cl¯ (iii) From general chemistry, we learned that ΔG° of a reaction that is the sum of two reactions is the sum of the ΔG°s of the two reactions. Thus, ΔG°(iii) = ΔG°(i) + ΔG°(ii). We also learned the relationships between ΔG° and E° and between ΔG° and K.
ΔG° = -nE°FΔG° = -RT lnKThus, it is possible to express ΔG°(i) in terms of E°(i).
ΔG°(i) = -FE°(i)Also, it is possible to express ΔG°(ii) in terms of K(ii).
ΔG°(ii) = -RT ln K(ii)Then, by adding ΔG°(i) and ΔG°(ii), ΔG°(iii) is obtained.
ΔG°(iii) = ΔG°(i) + ΔG°(ii) = -FE°(i) + -RT ln K(ii)Finally, by dividing ΔG°(iii) by nF, E°(iii) is obtained. Since n=1 for (iii),
E°(iii) = - ΔG°(iii)/F = E°(i) + RT/F ln KSPThis process shows that using E° for reaction (i) and Ksp for reaction (ii), we can calculate E° for reaction (iii)!
Using the same process, can you express E° for reaction (v) using E° for reaction (i) and Kf for reaction (iv)? Ag(NH3)p+? Note that reaction (v) is obtained when reaction (iv) is subtracted from reaction (i). HINT: Look at the post-lab work for a hint on what this should be!Ag+ + e¯ ⇌ Ag(s) (i) Ag+ + p NH3 ⇌ Ag(NH3)p+ (iv) Ag(NH3)p+ + e¯ ⇌ Ag(s) + p NH3 (v)

Lab Report Submission Details
Submit your lab report on Canvas as 1 combined PDF file. This submission should include:
- The completed answer sheet.
- Your lab notebook pages associated with this lab, which should include answers to the post-lab questions and challenge questions.
The grading rubric can be found on Canvas.
References:
- Harris, D. C. & Lucy, C. A. Quantitative Chemical Analysis, 10th ed.; W. H. Freeman: New York, NY, 2020
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please ask your instructor or TA.)
