D10.6 Kinetics and Equilibrium
Let us revisit the isomerization reaction
to see how a reaction’s kinetics relates to its equilibrium.
When we first considered the equilibrium of the cis–trans isomerization reaction, we noted that the reaction has a ΔrG° = +4.03 kJ/mol at 1000 K. Because the forward and reverse reaction have the same transition state, this ΔrG° value tells us that:
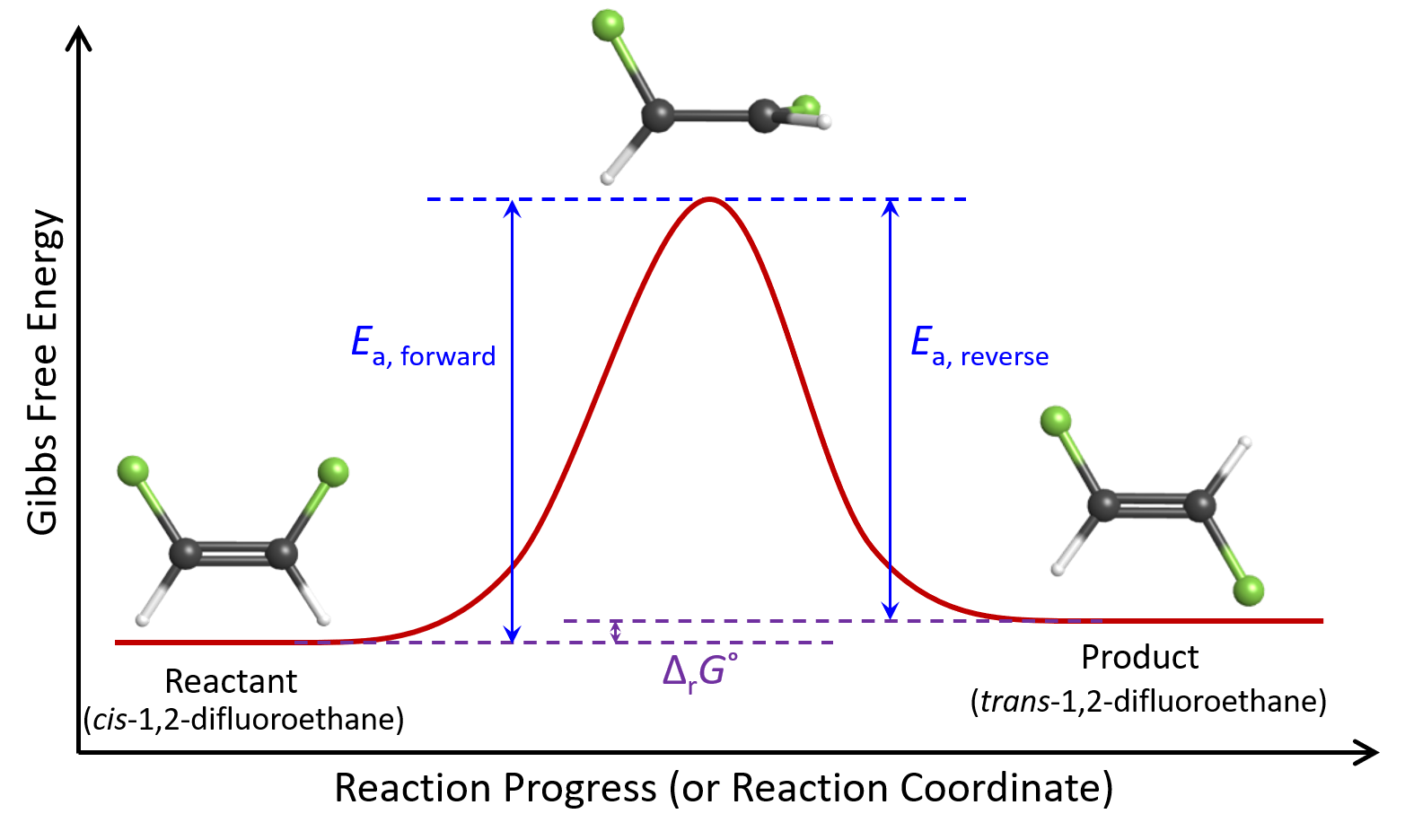
For this reaction, because Ea, forward > Ea, reverse, kforward would be smaller than kreverse. Using the Arrhenius equation, and assuming that Aforward = Areverse = A, we find that kforward = 0.62kreverse at 1000 K:
![Rendered by QuickLaTeX.com \begin{array}{rcl} \dfrac{k_{\text{forward}}}{k_{\text{reverse}}} &=& \dfrac{\text{A} e^{-E_{\text{a, forward}}/\text{RT}}}{\text{A} e^{-E_{\text{a, reverse}}/\text{RT}}} = e^{(-(E_{\text{a, forward}} - E_{\text{a, reverse}}))/\text{RT}} \\[1.5em] &=& e^{(-4030\;\text{J/mol})/((8.314\;\text{J/mol·K})(1000\;\text{K}))} = 0.62 \end{array}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-f169b0f33c5cad732d5e35ed479fb919_l3.png)
At the beginning of this reaction, there are only cis-1,2-difluoroethene molecules present. The rate of the forward reaction is:
As soon as the forward reaction produces some trans-1,2-difluoroethene, the reverse reaction begins to occur, and the rate of the reverse reaction is:
As the reaction proceeds, the rate of the forward reaction decreases as [cis-1,2-difluoroethene] decreases, and the rate of the reverse reaction increases as [trans-1,2-difluoroethene] increases.
Equilibrium is reached when
This results in the concentrations of both species remaining constant over time. But equilibrium is dynamic: each individual molecule is still constantly transforming back and forth between cis and trans forms.
The kinetic energy distribution of cis molecules is exactly the same as that of trans molecules because both isomers are at 1000 K. However, because Ea, forward > Ea, reverse, the fraction of cis molecules with KE > Ea, forward is smaller than the fraction of trans molecules with KE > Ea, reverse. This means that when a molecule is in the cis form, it is less likely to have enough energy to reach the transition state compared to when it is in the trans form. Therefore, on average, each molecule spends 62% time in the cis form and 38% time in the trans form, giving us K° = 0.38/0.62 = 0.61.
(The two K° values differ by 0.01 because of rounding error.)
A relationship between K° and the rate constantscan be derived from the fact that, at equilibrium, the rate of the forward reaction is equal to the rate of the reverse reaction:
To summarize the relationship between k, K°, and ΔrG°:
| ΔrG° | Kº | k | |
| < 0 | > 1 | kforward > kreverse | Product-favored at equilibrium. |
| > 0 | < 1 | kforward < kreverse | Reactant-favored at equilibrium. |
At a different temperature, both kforward and kreverse would have different values, and this would lead to a different equilibrium mixture. This is in agreement with the fact that both ΔrG° and K° are also temperature dependent. The temperature dependence of the rate constant can be calculated using the Arrhenius equation:
which tells us that the bigger the activation energy is the greater the effect of temperature on the rate constant is. For the cis-1,2-difluoroethene ⇄ trans-1,2-difluoroethene reaction, Ea, forward > Ea, reverse, therefore, kforward increases more rapidly with increasing temperature than does kreverse. This means that at a higher temperature, the equilibrium mixture would contain more product. For example, at 2000 K, where ΔrG° = 4.447 kJ/mol:
![Rendered by QuickLaTeX.com \begin{array}{rcl} \dfrac{k_{\text{forward}}}{k_{\text{reverse}}} &=& e^{(-(E_{\text{a, forward}} - E_{\text{a, reverse}}))/\text{RT}} \\[1.5em] &=& e^{(-4447\;\text{J/mol})/((8.314\;\text{J/mol·K})(2000\;\text{K}))} = 0.76 \end{array}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-cb87cb6695b897e4c8938c3464cfb520_l3.png)
Many reactions have greater ΔrG° than the cis–trans isomerization reaction, and, typically, useful reactions have large negative ΔrG° values. In such a case, kreverse << kforward.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂 (Note that we cannot answer questions via the google form. If you have a question, please post it on Piazza.)

