5 Resonance Structures and Formal Charge
Introduction
Learning Objectives for Resonance Structures and Formal Charge
- Draw resonance structures and evaluate their relative contributions to the resonance hybrid using formal charges and the octet rule.
| Bond Order, Bond Length, and Bond Strength | Resonance Structures | Bond Order Revisited | Calculating Formal Charge |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
Bond Order, Bond Length, and Bond Strength
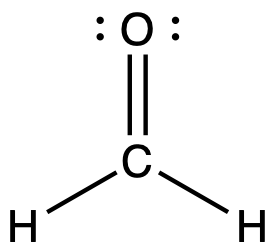
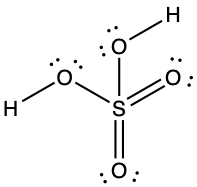
Looking at the structure of formaldehyde we can see that there is a double bond between the central carbon atom and the oxygen atom giving a CO bond order of two. The carbon is singly bonded to each hydrogen atom, which would give each CH bond orders of one.
Bond order is an index of bond strength: the higher the bond order, the stronger the bond. Bond strength is a measured quantity: the energy (in kJ/mol) required to break a chemical bond, tabulated in Appendix G. The stronger the bond, the more energy that is required to break the bond. This means that a C=O double bond is stronger than a C-O single bond, and the C=O double bond requires more energy to break than a C-O single bond. Bond length is the equilibrium distance between two nuclei. Higher bond orders generally correlate with shorter bond distances. The C=O double bond is shorter than the C-O single bond.
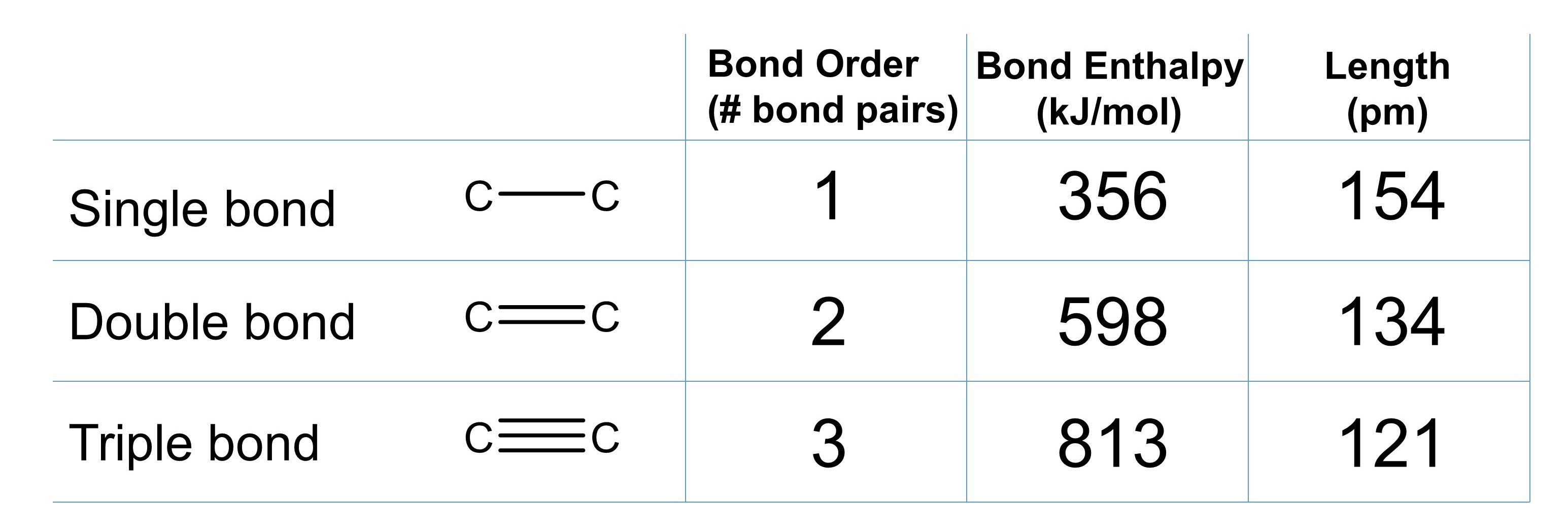
We can apply these same concepts to carbon-carbon single, double, and triple bonds to compare how bond order, bond length and bond strength are related (Figure 1).
Resonance Structures
Following the five steps for drawing a Lewis structure we can determine a valid Lewis structure for NO2- :
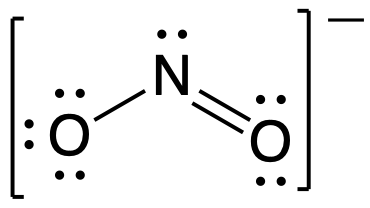
If this representation is the only correct resonance structure, we would expect the molecule to be asymmetric, meaning the bond lengths between the central nitrogen and the oxygen atoms would be different. A double bond between two atoms is shorter (and stronger) than a single bond between the same two atoms. As we will see from the discussion of formal charge below, we would also expect that the electrons would be distributed such that the negative charge would be present on one oxygen atom. Experimental evidence, however, establishes that nitrite is symmetric and that both N–O bonds in NO2− have the same strength and length. The two N-O bonds and the two oxygen atoms in nitrite are equivalent in all chemical and physical properties.
It is not possible to write a single Lewis structure for NO2− which accurately represents the electronic structure. Instead, we use the concept of resonance: if two or more Lewis structures with the same arrangement of atoms can be written for a molecule or ion, the actual distribution of electrons is a weighted average of the valid Lewis structures. Therefore, two valid Lewis structures must be drawn to represent the bonding in the nitrite ion, NO2-.
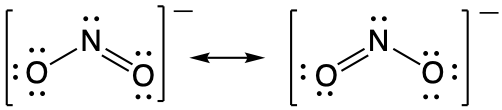
The two headed arrow that connects two (or more) valid Lewis structures is important. It communicates that we're talking about resonance structures and not a chemical reaction (which is signified by a single-headed arrow, →) or equilibrium (which is signified by two half-arrows, ⇌).
The nitrite ion is an example of equivalent resonance, which means that the two bonds are identical. Both NO bonds have the same atoms involved, the same length, and require the same energy added to break them. Thus, the two NO bonds are identical. The actual distribution of electrons in each of the NO bonds in NO2− is the weighted average of a double bond and a single bond. Since the bonds are equivalent, they are equally weighted, so each connection between nitrogen and oxygen has an N-O bond order of 1.5.
The actual electronic structure of the molecule (the weighted average of the resonance forms) is represented by a resonance hybrid of the individual resonance forms. Thus, the electronic structure of the NO2− ion is shown as:
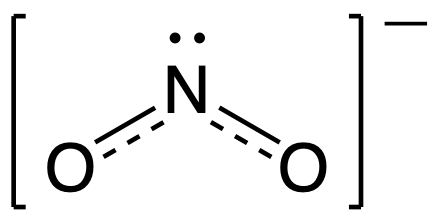
We should remember that a molecule described as a resonance hybrid never possesses an electronic structure described by either resonance form. It does not fluctuate between resonance forms; rather, the actual electronic structure is always the weighted average of that shown by all resonance forms.
Notice that the atoms did not change position in the nitrite example of resonance. If atom positions change with respect to one another, then this is not an example of resonance. Instead, the molecules are isomers involved in a chemical change, and that will be explored in future courses.
The carbonate anion, CO32−, provides a second example of a polyatomic ion with equivalent resonance or equally weighted resonance structures:
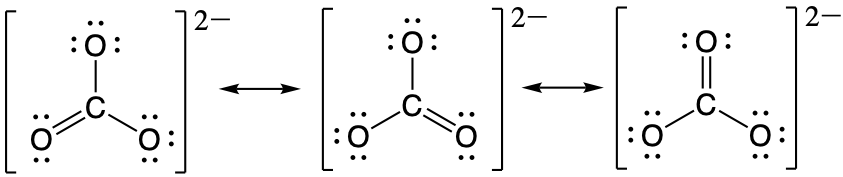
One oxygen atom must have a double bond to carbon to complete the octet on the central atom. All oxygen atoms, however, are equivalent, and the Lewis structure could be drawn with the double bond between carbon and any one of the three oxygen atoms. This gives rise to three equivalent resonance forms of the carbonate ion. Because we can write three equivalent resonance structures, we know that the actual arrangement of electrons in the carbonate ion is the equally weighted average of the three structures. These three structures highlight the symmetric bonding and distribution of electrons present in the carbonate ion. Again, experimental evidence establishes the symmetry of carbonate and shows that all three CO bonds are equivalent (bond length and bond strength) and that each oxygen atom is chemically equivalent.
Bond Order Revisited
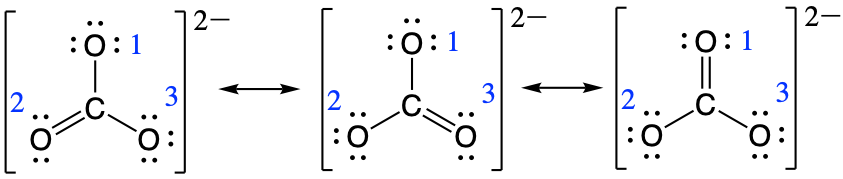
So for determining the bond order between carbon and oxygen number one the calculation would be as follows:
bond order for oxygen one = [latex]\frac{1+1+2}{3} = \frac{4}{3}[/latex]
and for oxygen number two:
bond order for oxygen two = [latex]\frac{2+1+1}{3} = \frac{4}{3}[/latex]
and for oxygen number three:
bond order for oxygen three = [latex]\frac{1+2+1}{3} = \frac{4}{3}[/latex]
This gives the bond order between the central carbon and each oxygen atom as being 4/3. This means that in the resonance hybrid each bond between carbon and oxygen has bond character that is between that of a single bond and a double bond, which we have proven experimentally. The resonance hybrid for CO32- is provided below:
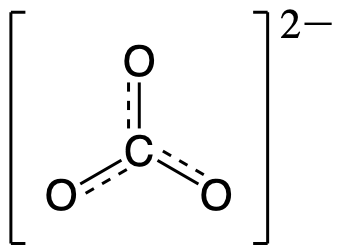
As indicated by the resonance hybrid and the bond order calculation, each bond between carbon and oxygen has a total bond order between that of a single bond (bond order = 1) and a double bond (bond order = 2). This is consistent with all of the experimental observations of the bond lengths and the reactivity of each atom, as well as theoretical predictions of the electronic structure. The nature of each of the bonds in a double bond will be explored in a later module.
All of the resonance structures we've considered up to this point have been equivalent to one another. That is, the location of the double bond had an equal likelihood of being associated with any of the oxygen atoms in NO2- or CO32- so each resonance structure has equal stability. There are molecules where one resonance structure may not be as stable as another while still satisfying the octet rule. We are able to compare these resonance structures to one another using a concept known as formal charge.

The online Lewis Structure Maker includes many examples to practice drawing resonance structures.
Calculating Formal Charge
The formal charge of an atom in a molecule is the hypothetical charge the atom would have if we could redistribute the electrons in the bonds evenly between the atoms. Another way of saying this is that formal charge results when we take the number of valence electrons of a neutral atom, subtract the nonbonding electrons, and then subtract half the number of bonding electrons (distribute them evenly to each of the two atoms that are bonded).
Thus, we calculate formal charge as follows:

By subtracting one-half the number of bonding electrons, we essentially assign half the bonding electrons to each atom. This implicitly assumes that these bonding electrons are shared relatively equally, as in covalent bonding. Since each bond represents two electrons, we can also count the number of bonds connected to that atom in the Lewis structure and the equation becomes:

The previous two equations are both common ways of calculating formal charge and will yield the same answer. The sum of the formal charges on all atoms in a neutral molecule is zero; the sum of the formal charges on a polyatomic ion is the charge on the ion.
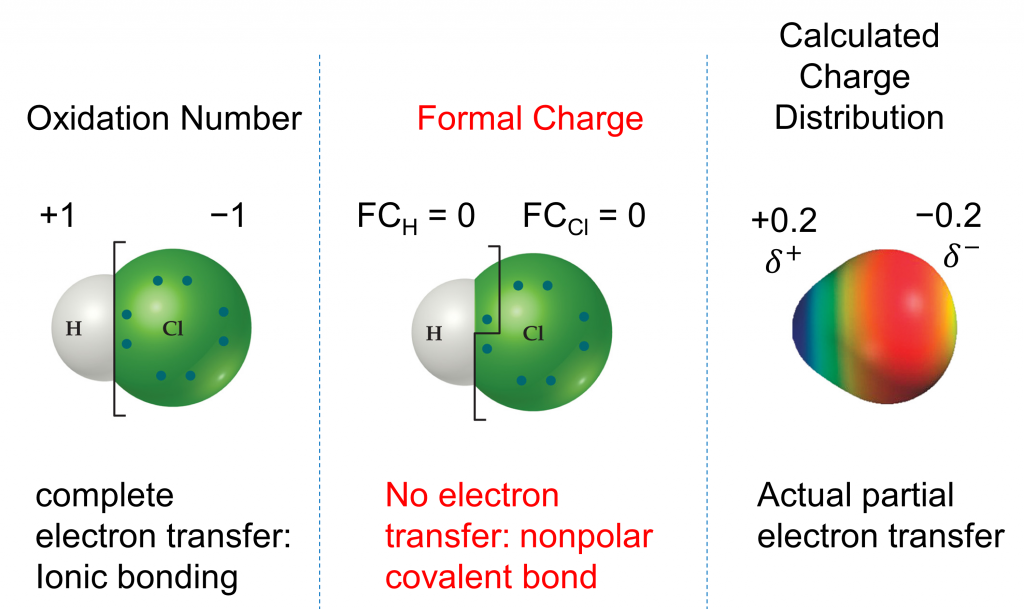
We must remember that the formal charge calculated for an atom is not the actual charge of the atom in the molecule. Formal charge is only a useful bookkeeping procedure; it does not indicate the presence of actual charges. We can compare three different ways of thinking about the H-Cl bond using different concepts covered so far (as summarized in Figure 2). The calculated charge distribution illustrates the polar bond observed experimentally.
Example 1
Calculating Formal Charge from Lewis Structures
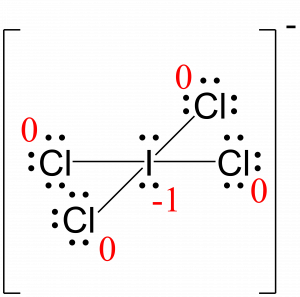
Assign formal charges to each atom in the interhalogen ion ICl4−.
Solution
- We divide the bonding electron pairs equally for all I–Cl bonds:
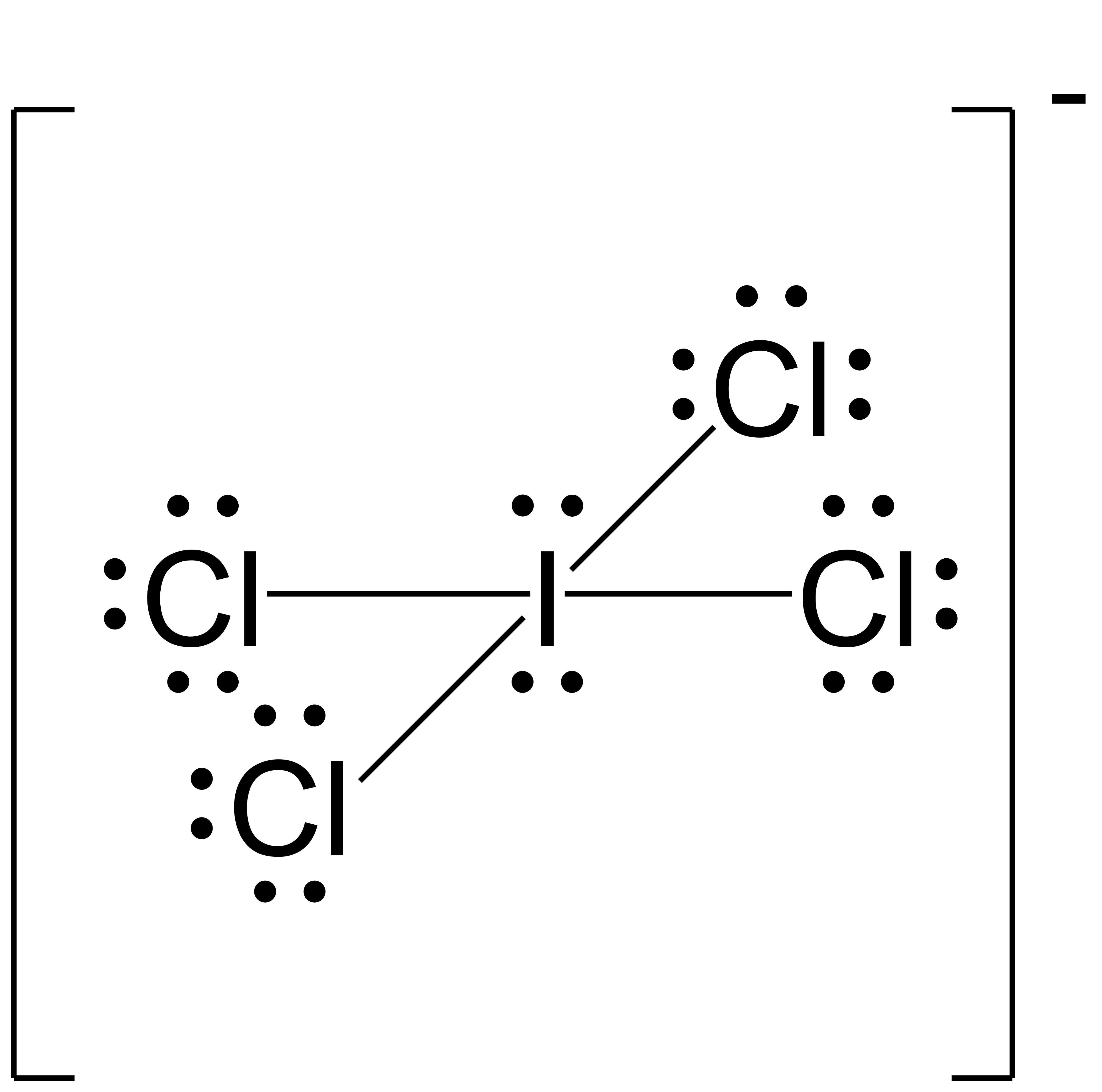
- We assign lone pairs of electrons to their atoms. Each Cl atom now has 6 unshared electrons and 2 bonding electrons, and the I atom has 4 unshared electrons and 8 bonding electrons.
- Subtract the number of unshared electrons + ½ number of bonding electrons from the number of valence electrons for the neutral atom:
I: 7 – (4 + ½ (8)) = –1
Cl: 7 – (6 + ½ (2)) = 0
The sum of the formal charges of all the atoms equals –1, which is identical to the charge of the ion (–1).
The formal charges for each atom are drawn next to them in red for the final Lewis structure provided below.
Check Your Learning
Calculate the formal charge for each atom in the carbon monoxide molecule:
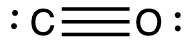
Answer:
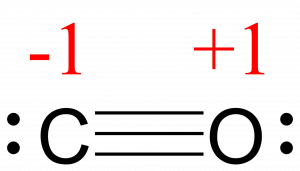
C −1, O +1
The formal charges for each atom are drawn next to them in red for the final Lewis structure provided below.
Example 2
Calculating Formal Charge from Lewis Structures
Assign formal charges to each atom in the interhalogen molecule BrCl3.
Solution
- Assign one of the electrons in each Br–Cl bond to the Br atom and one to the Cl atom in that bond:
- Assign the lone pairs to their atom. Now each Cl atom has 6 unshared electrons and 2 bonding electrons, and the Br atom has 4 unshared electrons and 6 bonding electrons.
- Subtract this number from the number of valence electrons for the neutral atom. This gives the formal charge:
Br: 7 – (4 + ½ (6)) = 0
Cl: 7 – (6 + ½ (2)) = 0
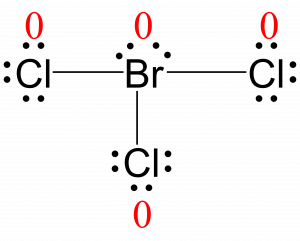
All atoms in BrCl3 have a formal charge of zero, and the sum of the formal charges totals zero, as it must in a neutral molecule.
The formal charges for each atom are drawn next to them in red for the final Lewis structure provided below.
Check Your Learning
Determine the formal charge for each atom in NCl3.
Answer:
N: 0; all three Cl atoms: 0
The formal charges for each atom are drawn next to them in red for the final Lewis structure provided below.
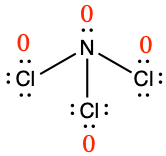
Using Formal Charge to Predict Resonance Structure Contributions
As discussed previously, molecules often have more than one valid Lewis structure. These resonance structures contribute to the overall resonance hybrid for a given molecule. However, not all resonance structures contribute equally to the bonding of a molecule. The most stable individual resonance structure (and thus the largest contributor to the resonance hybrid) tends to:
- Minimize formal charges on atoms.
- Place negative formal charges on more electronegative atoms.
To see how these guidelines apply, let us consider some possible structures for carbon dioxide, CO2, with carbon as the central atom. We can draw three possibilities for the structure:
![]()
Assigning formal charge to each atom gives us the following values:
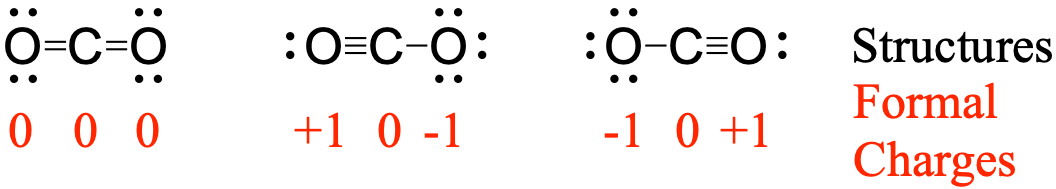
Computational chemistry predicts that the left structure (which minimizes formal charge since all atoms have a formal charge of zero) contributes the greatest to the bonding in CO2 (~50%). The other two structures contribute less to the bonding structure (~25% each). Thus, CO2 has non-equivalent resonance structures. Formal charges help us estimate the relative contributions by each resonance structure when non-equivalent resonance structures contribute to the resonance hybrid.
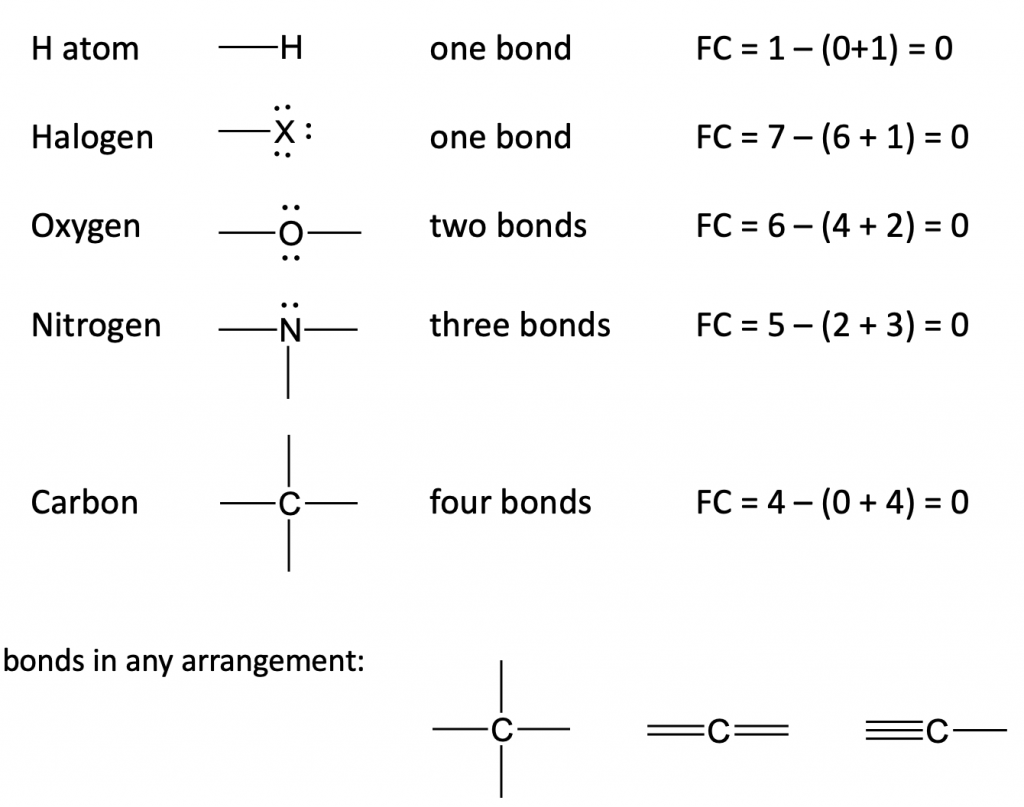
Commonly Found "Building Blocks" of Molecules with Zero Formal Charge
Many commonly found elements in molecules have zero formal charge. By counting the number of electrons and bonds around an element and whether that gives the element a formal charge of zero will help us quickly recognize how that impacts the stability and reactivity of the molecule as a whole. The chart below summarizes some common elements and their bonding patterns that give a zero formal charge.
Example 3
Using Formal Charge to Determine Major Resonance Structure
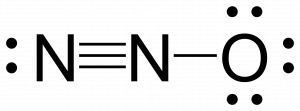
Nitrous oxide, N2O, commonly known as laughing gas, is used as an anesthetic in minor surgeries, such as the routine extraction of wisdom teeth. Which structure is the major contributor to the resonance hybrid?
![]()
Solution
Determining formal charge yields the following:

The structure in which the oxygen carries the negative formal charge is the major resonance contributor since oxygen is more electronegative than nitrogen. Additionally the number of atoms with formal charges are minimized since one atom has a formal charge of 0.
Check Your Learning
Using formal charge, rationalize which structure contributes the most for the thiocyanate (SCN−) ion?
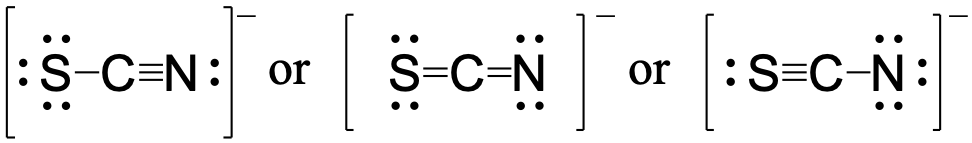
Answer:
First, assign formal charges:
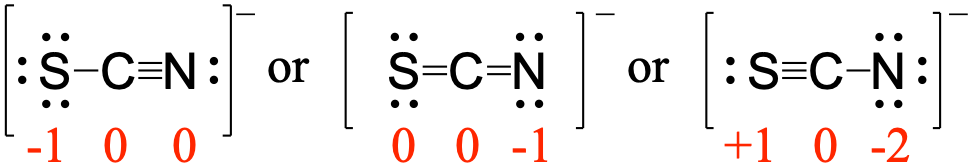
Major contributor:
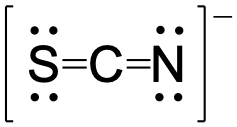
In this resonance form of the thiocyanate ion, the formal charges are as follows:
S: 0
C: 0
N: -1
Since nitrogen is more electronegative than sulfur, placing the negative formal charge on nitrogen is favorable compared to the other two options above.
Key Concepts and Summary
In a Lewis structure, formal charges can be assigned to each atom by treating each bond as if one-half of the electrons are assigned to each atom. These hypothetical formal charges are a guide to determining the most appropriate Lewis structure. A structure in which the formal charges are as close to zero as possible is preferred. Resonance occurs in cases where two or more Lewis structures with identical arrangements of atoms but different distributions of electrons can be written. The actual distribution of electrons (the resonance hybrid) is an average of the distribution indicated by the individual Lewis structures (the resonance forms) and does not possess an electronic structure depicted by an individual resonance form.
Key Equations
- formal charge = number of valence shell electrons (free atom) − number of lone pair electrons − [latex]\frac{1}{2}[/latex] number of bonding electrons
Glossary
- bond order
- The number of electron-pair bonds connecting two atoms
- formal charge
- charge that would result on an atom by taking the number of valence electrons on the neutral atom and subtracting the nonbonding electrons and the number of bonds (one-half of the bonding electrons)
- molecular structure
- arrangement of atoms in a molecule or ion
- resonance
- situation in which one Lewis structure is insufficient to describe the bonding in a molecule and the average of multiple structures is observed
- resonance forms
- two or more Lewis structures that have the same arrangement of atoms but different arrangements of electrons
- resonance hybrid
- average of the resonance forms shown by the individual Lewis structures
Chemistry End of Section Exercises
- Write resonance forms that describe the distribution of electrons in each of these molecules or ions.
- sulfur dioxide, SO2
- carbonate ion, CO32−
- hydrogen carbonate ion, HCO3− (C is bonded to an OH group and two O atoms)
- pyridine:
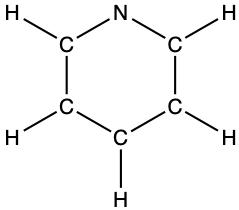
- the allyl ion:
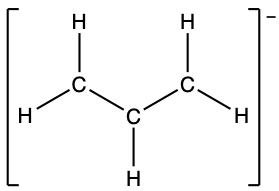
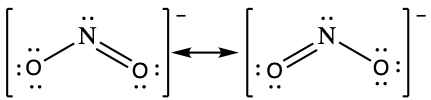
- Sodium nitrite, which has been used to preserve bacon and other meats, is an ionic compound. Write the resonance forms of the nitrite ion, NO2–.
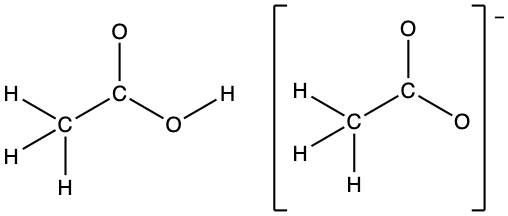
- In terms of the bonds present, explain why acetic acid, CH3CO2H, contains two distinct types of carbon-oxygen bonds, whereas the acetate ion, formed by loss of a hydrogen ion from acetic acid, only contains one type of carbon-oxygen bond. The skeleton structures of these species are shown:
- Write the Lewis structures for the following, and include resonance structures where appropriate. Indicate which has the strongest carbon-oxygen bond.
- CO2
- CO
- Toothpastes containing sodium hydrogen carbonate (sodium bicarbonate) and hydrogen peroxide are widely used. Write Lewis structures for the hydrogen carbonate ion and hydrogen peroxide molecule, with resonance forms where appropriate.
- Determine the formal charge of each element in the following:
- HCl
- CF4
- PCl3
- PF5
- Calculate the formal charge of chlorine in the molecules Cl2, BeCl2, and ClF5.
- Draw all important or highly contributing resonance structures for each of these compounds. Determine the formal charge on each atom in each of the resonance structures:
- O3
- SO2
- NO2−
- NO3−
- Based on formal charge considerations, which of the following would likely be the correct arrangement of atoms in nitrosyl chloride: ClNO or ClON?
- Based on formal charge considerations, which of the following would likely be the correct arrangement of atoms in hypochlorous acid: HOCl or OClH?
- Based on formal charge considerations, which of the following would likely be the correct arrangement of atoms in sulfur dioxide: OSO or SOO?
- Draw a structure of hydroxylamine, H3NO, and assign formal charges; look up the structure. Is the actual structure consistent with the formal charges?
- Write the Lewis structure and chemical formula of the compound with a molar mass of about 70 g/mol that contains 19.7% nitrogen and 80.3% fluorine by mass, and determine the formal charge of the atoms in this compound.
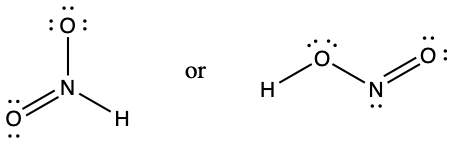
- Which of the following structures would we expect for nitrous acid? Determine the formal charges:
- Sulfuric acid is the industrial chemical produced in greatest quantity worldwide. About 90 billion pounds are produced each year in the United States alone. Write the Lewis structure for sulfuric acid, H2SO4, which has two oxygen atoms and two OH groups bonded to the sulfur.
Answers to Chemistry End of Section Exercises
- (a)
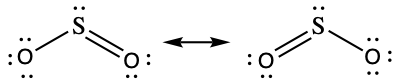
(b)
(c)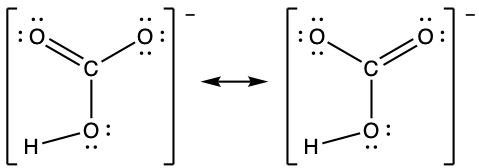
(d)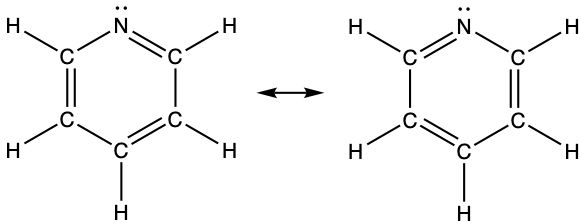
(e)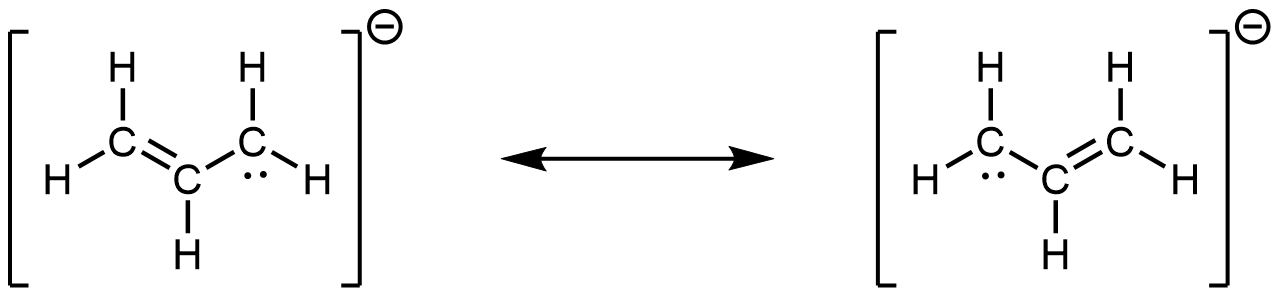
- Acetic acid has a C=O double bond and a C-O single bond. The acetate ion has only one type of carbon-oxygen bond, as illustrated by its resonance structures. The negative charge is delocalized on both the oxygen atoms and both carbon-oxygen bonds are of the same length.
- (a)
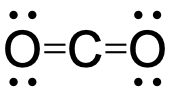 ; (b)
; (b)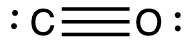 ; CO has the strongest carbon-oxygen bond because there is a triple bond joining C and O. CO2 has double bonds.
; CO has the strongest carbon-oxygen bond because there is a triple bond joining C and O. CO2 has double bonds. - hydrogen carbonate ion:
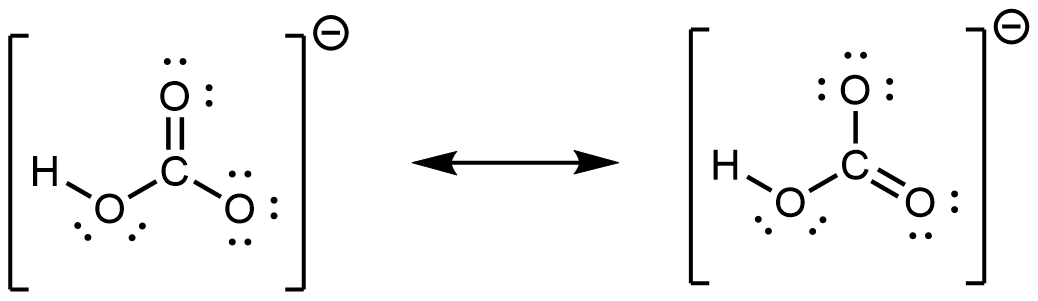 hydrogen peroxide:
hydrogen peroxide: 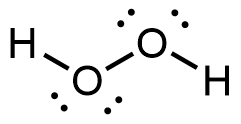
- (a) H: 0, Cl: 0; (b) C: 0, F: 0; (c) P: 0, Cl 0; (d) P: 0, F: 0
- Cl in Cl2: 0; Cl in BeCl2: 0; Cl in ClF5: 0
- (a)
 ;
;
(b)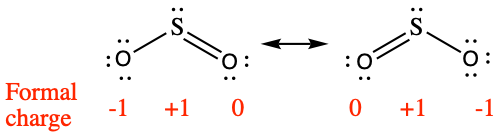 ;
;
(c)![[Two Lewis structures are shown, with brackets surrounding each with a superscripted negative sign and a double ended arrow in between. The left structure shows a nitrogen atom with one lone pair of electrons single bonded to an oxygen atom with three lone pairs of electrons and double bonded to an oxygen atom with two lone pairs of electrons. The symbols and numbers below this structure read “open parenthesis, 0, close parenthesis, open parenthesis, 0, close parenthesis, open parenthesis, negative 1, close parenthesis. The right structure appears as a mirror image of the left and the symbols and numbers below this structure read “open parenthesis, negative 1, close parenthesis, open parenthesis, 0, close parenthesis, open parenthesis, 0, close parenthesis.]](https://wisc.pb.unizin.org/app/uploads/sites/293/2019/06/M8Q3_Nitrite_Resonance_withFormalCharge.png) ;
;
(d)![[Three Lewis structures are shown, with brackets surrounding each with a superscripted negative sign and a double ended arrow in between. The left structure shows a nitrogen atom single bonded to two oxygen atoms, each with three lone pairs of electrons and double bonded to an oxygen atom with two lone pairs of electrons. The single bonded oxygen atoms are labeled, from the top of the structure and going clockwise, “open parenthesis, negative 1, close parenthesis, open parenthesis, positive 1, close parenthesis”. The symbols and numbers below this structure read “open parenthesis, 0, close parenthesis, open parenthesis, negative 1, close parenthesis. The middle structure shows a nitrogen atom single bonded to two oxygen atoms, each with three lone pairs of electrons, one of which is labeled “open parenthesis, positive 1, close parenthesis” and double bonded to an oxygen atom with two lone pairs of electrons labeled “open parenthesis, 0, close parenthesis”. The symbols and numbers below this structure read “open parenthesis, negative 1, close parenthesis, open parenthesis, negative 1, close parenthesis. The right structure shows a nitrogen atom single bonded to two oxygen atoms, each with three lone pairs of electrons and double bonded to an oxygen atom with two lone pairs of electrons. One of the single bonded oxygen atoms is labeled, “open parenthesis, negative 1, close parenthesis while the double bonded oxygen is labeled, “open parenthesis, positive 1, close parenthesis”. The symbols and numbers below this structure read “open parenthesis, negative 1, close parenthesis” and “open parenthesis, 0, close parenthesis”.]](https://wisc.pb.unizin.org/app/uploads/sites/293/2019/06/M8Q3-Nitrate_resonance_with_FormalCharge.png)
- ClNO
- HOCl
- OSO
- The structure that gives zero formal charges is consistent with the actual structure:
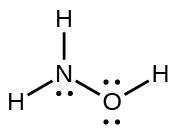
- NF3,
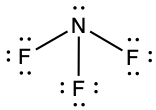 , N: 0, F: 0
, N: 0, F: 0 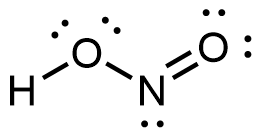 , H: 0, O: 0, N: 0
, H: 0, O: 0, N: 0