Part II. Our first agent-based evolutionary model
II-3. Noise and initial conditions
1. Goal
Our goal is to extend the model we have created in the previous chapter by adding two features that will prove very useful:
- The possibility of setting initial conditions explicitly. This is an important feature because initial conditions can be very relevant for the evolution of a system.
- The possibility that revising agents select a strategy at random with a small probability. This type of noise in the revision process may account for experimentation or errors in economic settings, or for mutations in biological contexts. The inclusion of noise in a model can sometimes change its dynamic behavior dramatically, even creating new attractors. This is important because dynamic features of a model –such as attractors, cycles, repellors, and other patterns– that are not robust to the inclusion of small noise may not correspond to relevant properties of the real-world system that we aim to understand. Besides, as a positive side-effect, adding small amounts of noise to a model often makes the analysis of its dynamics easier to undertake.
2. Motivation. Noise in rock, paper, scissors
In the previous chapter we saw that simulations of the Rock-Paper-Scissors game under the imitate-if-better decision rule end up in a state where everyone is choosing the same strategy. Can you guess what will happen in this model if we add a little bit of noise?
3. Description of the model
In this model, there is a population of n-of-players agents who repeatedly play a symmetric 2-player game with any number of strategies. The payoffs of the game are determined by the user in the form of a matrix [ [A00 A01 … A0n] [A10 A11 … A1n] … [An0 An1 … Ann] ] containing the payoffs Aij that an agent playing strategy i obtains when meeting an agent playing strategy j (i, j ∈ {0, 1, …, n}). The number of strategies is inferred from the number of rows in the payoff matrix.
Initial conditions are set with parameter n-of-players-for-each-strategy, using a list of the form [a0 a1 … an], where item ai is the initial number of agents with strategy i. Thus, the total number of agents is the sum of all elements in this list. From then onwards, the following sequence of events –which defines a tick– is repeatedly executed:
- Every agent obtains a payoff by selecting another agent at random and playing the game.
- With probability prob-revision, individual agents are given the opportunity to revise their strategies. In that case, with probability noise, the revising agent will adopt a random strategy; and with probability (1 – noise), the revising agent will choose her strategy following the imitate if better rule:
Look at another (randomly selected) agent and adopt her strategy if and only if her payoff was greater than yours.
All agents who revise their strategies within the same tick do it simultaneously (i.e. synchronously).
The model shows the evolution of the number of agents choosing each of the possible strategies at the end of every tick.
 4. Interface design
4. Interface design
We depart from the model we developed in the previous chapter (so if you want to preserve it, now is a good time to duplicate it).
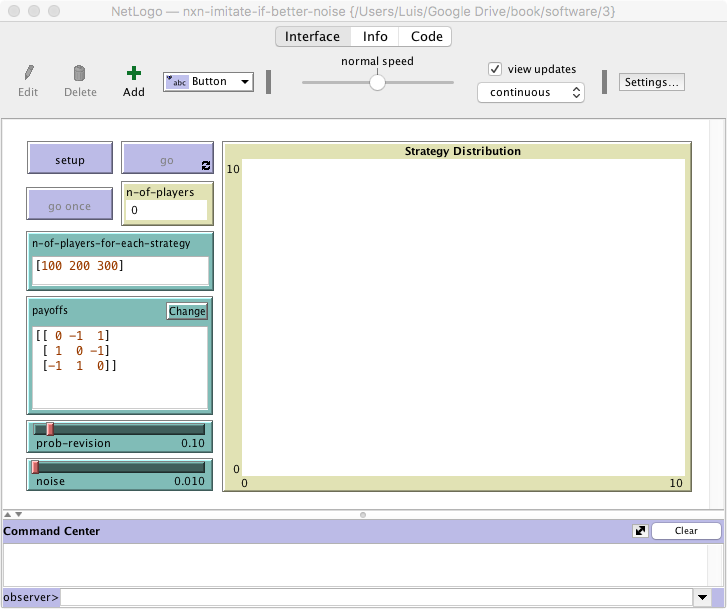
The new interface (see figure 1 above) requires a few simple modifications:
- Create an input box to let the user set the initial number of players using each strategy.
In the Interface tab, add an input box with associated global variable n-of-players-for-each-strategy. Set the input box type to “String (reporter)”.
- Note that the total number of players (which was previously set using a slider with associated global variable n-of-players) will now be computed totaling the items of the list n-of-players-for-each-strategy. Thus, we should remove the slider, and include the global variable n-of-players in the Code tab.
globals [ payoff-matrix n-of-strategies n-of-players ]
- Add a monitor to show the total number of players. This number will be stored in the global variable n-of-players, so the monitor must show the value of this variable.
In the Interface tab, create a monitor. In the “Reporter” box write the name of the global variable n-of-players.
- Create a slider to choose the value of parameter noise.
In the Interface tab, create a slider with associated global variable noise. Choose limit values 0 and 1, and an increment of 0.001.
 5. Code
5. Code
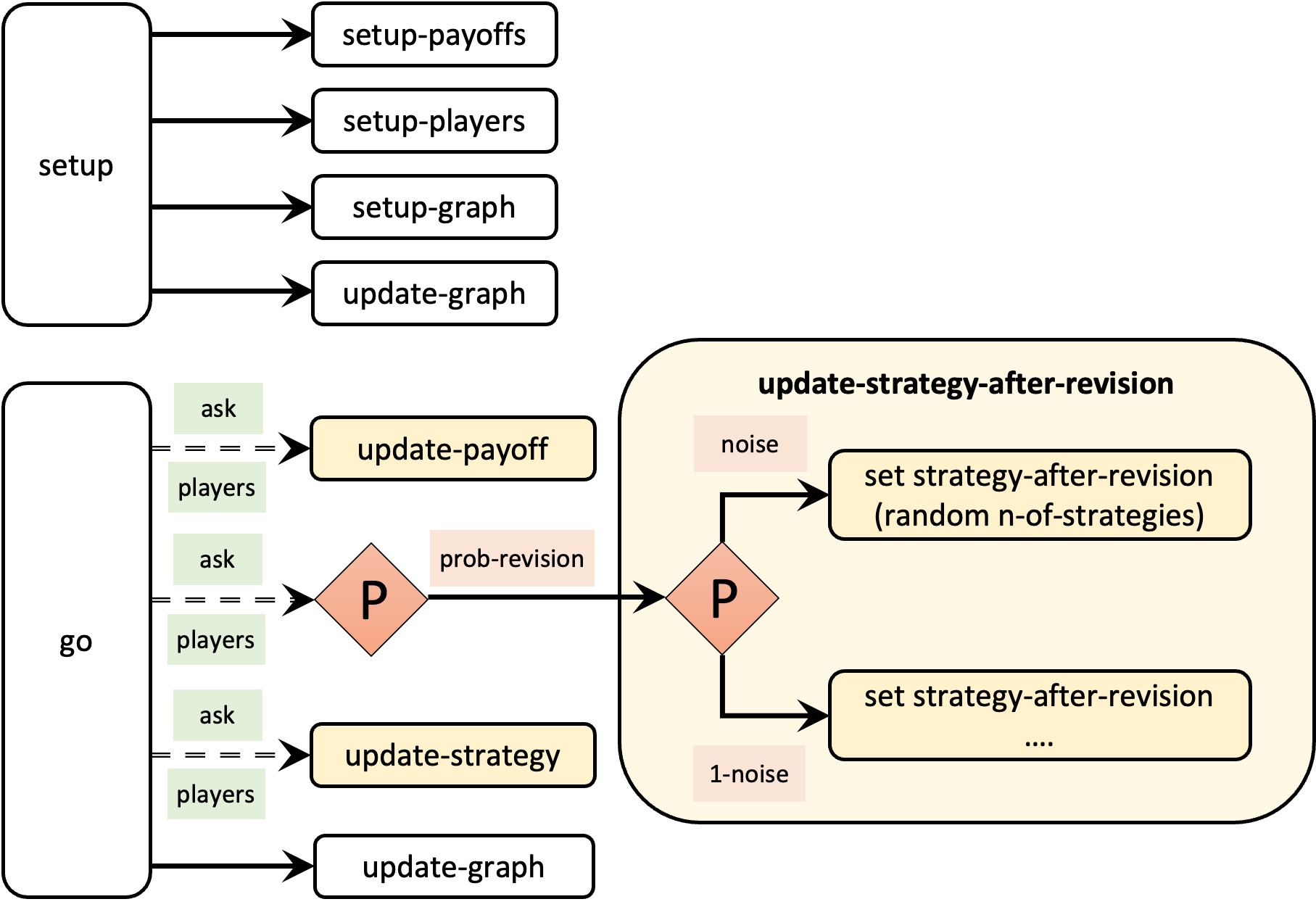
5.1. Skeleton of the code
5.2. Global variables and individually-owned variables
The only change required regarding user-defined variables is the inclusion of global variable n-of-players in the Code tab, as explained in the previous section.
5.3. Setup procedures
To read the initial conditions specified with parameter n-of-players-for-each-strategy and set up the players accordingly, it is clear that we only have to modify the code in procedure to setup-players. Note that making our code modular, by implementing short procedures with specific tasks and meaningful names, makes our life easy at the time of extending the model.
to setup-players
Since the content of parameter n-of-players-for-each-strategy is a string, the first we should do is to turn it into a list that we can use in our code. To this end, we use the primitive read-from-string and store its output in a new local variable named initial-distribution, as follows:
let initial-distribution read-from-string n-of-players-for-each-strategy
Next, we can check that the number of elements in the list initial-distribution matches the number of possible strategies (i.e. the number of rows in the payoff matrix stored in payoff-matrix), and issue a warning message otherwise, using primitive user-message. Naturally, this is by no means compulsory, but it is a thoughtful touch that will make our program more user-friendly. To this end, we can use the code below.
if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" ;; "\n" is used to jump to the next line "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] ;; It is not necessary to show the user ;; the value of n-of-players-for-each-strategy ;; and payoffs again, ;; but when creating an error message, ;; it is good practice to give the user ;; as much information as possible, ;; so the error can be easily corrected.
Now, let us create as many players using each strategy as indicated by the values in the list initial-distribution. For instance, if initial-distribution is [5 10 15], we should create 5 players with strategy 0, 10 players with strategy 1, and 15 players with strategy 2. Since we want to perform a task for each element of the list, primitive foreach will be handy.
Besides going through each element on the list using foreach, we would also like to keep track of the position being read on the list, which is the corresponding strategy number. For this, we create a counter i which we start at 0:
let i 0 foreach initial-distribution [ j -> create-players j [ set payoff 0 set strategy i set strategy-after-revision strategy ] set i (i + 1) ]
Finally, let us set the value of the global variable n-of-players:
set n-of-players count players
The line above concludes the definition of procedure to setup-players, and the implementation of the user-chosen initial conditions.
5.4. Go and other main procedures
To implement the choice of a random strategy with probability noise by revising agents, we have to modify the code of procedure to update-strategy-after-revision. At present, the code of this procedure looks as follows:
to update-strategy-after-revision let observed-player one-of other players if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] end
We can implement the noise feature using primitive ifelse, whose structure is
ifelse CONDITION [ COMMANDS EXECUTED IF CONDITION IS TRUE ] [ COMMANDS EXECUTED IF CONDITION IS FALSE ]
In our case, the CONDITION should be true with probability noise. Bearing all this in mind, the final code for procedure to update-strategy-after-revision could be as follows:
to update-strategy-after-revision ifelse random-float 1 < noise ;; the condition is true with probability noise [ ;; code to be executed if there is noise set strategy-after-revision (random n-of-strategies) ] [ ;; code to be executed if there is no noise let observed-player one-of other players if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end
5.5. Complete code in the Code tab
The Code tab is ready!
globals [ payoff-matrix n-of-strategies n-of-players ] breed [players player] players-own [ strategy strategy-after-revision payoff ] to setup clear-all setup-payoffs setup-players setup-graph reset-ticks update-graph end to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix end to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] let i 0 foreach initial-distribution [ j -> create-players j [ set payoff 0 set strategy i set strategy-after-revision strategy ] set i (i + 1) ] set n-of-players count players end to setup-graph set-current-plot "Strategy Distribution" foreach (range n-of-strategies) [ i -> create-temporary-plot-pen (word i) set-plot-pen-mode 1 set-plot-pen-color 25 + 40 * i ] end to go ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph end to update-payoff let mate one-of other players set payoff item ([strategy] of mate) (item strategy payoff-matrix) end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ let observed-player one-of other players if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] ] end to update-strategy set strategy strategy-after-revision end to update-graph let strategy-numbers (range n-of-strategies) let strategy-frequencies map [ n -> count players with [strategy = n] / n-of-players ] strategy-numbers set-current-plot "Strategy Distribution" let bar 1 foreach strategy-numbers [ n -> set-current-plot-pen (word n) plotxy ticks bar set bar (bar - (item n strategy-frequencies)) ] set-plot-y-range 0 1 end
6. Sample run
Now that we have implemented the model, we can use it to answer the question posed above: Will adding a bit of noise change the dynamics of the Rock-Paper-Scissors game under the imitate-if-better decision rule? To do that, let us use the same setting as in the previous chapter, i.e. payoffs = [[0 -1 1][1 0 -1][-1 1 0]] and prob-revision = 0.1. To have 500 agents and initial conditions close to random, we can set n-of-players-for-each-strategy = [167 167 166]. Finally, let us use noise = 0.01. The following video shows a representative run with these settings.
As you can see, noise dampens the amplitude of the cycles, so the monomorphic states where only one strategy is chosen by the whole population are not observed anymore.[1] Even if at some point one strategy went extinct, noise would bring it back into existence. Thus, the model with noise = 0.01 exhibits an everlasting pattern of cycles of varying amplitudes. This contrasts with the model without noise, which necessarily ends up in one of only three possible final states.
7. Exercises
You can use the following link to download the complete NetLogo model: nxn-imitate-if-better-noise.nlogo.

Exercise 1. Consider a Prisoner’s Dilemma with payoffs [[2 4][1 3]] where strategy 0 is “Defect” and strategy 1 is “Cooperate”. Set prob-revision to 0.1 and noise to 0. Set the initial number of players using each strategy, i.e. n-of-players-for-each-strategy, to [0 200], i.e., everybody plays “Cooperate”. Press the button and run the model. While it is running, move the noise slider slightly rightward to introduce some small noise. Can you explain what happens?
Exercise 2. Consider a Rock-Paper-Scissors game with payoff matrix [[0 -1 1][1 0 -1][-1 1 0]]. Set prob-revision to 0.1 and noise to 0. Set the initial number of players using each strategy, i.e. n-of-players-for-each-strategy, to [100 100 100]. Press the button and run the model for a while. While it is running, click on the noise slider to set its value to 0.001. Can you explain what happens?
Exercise 3. Consider a game with payoff matrix [[1 1 0][1 1 1][0 1 1]]. Set prob-revision to 0.1, noise to 0.05, and the initial number of players using each strategy, i.e. n-of-players-for-each-strategy, to [500 0 500]. Press the button and run the model for a while (then press the button again to change the initial conditions). Can you explain what happens?
Exercise 4. Consider a game with n players and s strategies, with noise equal to 1. What is the infinite-horizon probability distribution of the number of players using each strategy?
![]() Exercise 5. Imagine that you’d like to run this model faster, and you are not interested in the plot. This is a common scenario when you want to conduct large-scale computational experiments. What lines of code could you comment out?
Exercise 5. Imagine that you’d like to run this model faster, and you are not interested in the plot. This is a common scenario when you want to conduct large-scale computational experiments. What lines of code could you comment out?
![]() Exercise 6. Note that you can modify the values of parameters prob-revision and noise at runtime with immediate effect on the dynamics of the model. How could you implement the possibility of changing the number of players in the population with immediate effect on the model?
Exercise 6. Note that you can modify the values of parameters prob-revision and noise at runtime with immediate effect on the dynamics of the model. How could you implement the possibility of changing the number of players in the population with immediate effect on the model?
- In this model with noise, every state will be observed at some point if we wait for long enough, but long enough might be a really long time (e.g. centuries). ↵

