Part III. Spatial interactions on a grid
III-4. Other types of neighborhoods and other decision rules
1. Goal
Our goal in this chapter is to extend the model we have created in the previous chapter by adding two features that are crucial to assess the impact of space on evolutionary models:
- The possibility to model different types of neighborhoods of arbitrary size. Besides Moore neighborhoods, we will implement Von Neumann neighborhoods, and both of them of any size.
- The possibility to model other decision rules besides the imitate the best neighbor rule. In particular, we will implement the imitative pairwise-difference rule, the imitate if better rule, the imitative positive proportional rule, and the Fermi rule.[1]
2. Motivation. The impact of decision rules
In chapter III-2 we explored the impact of different assumptions on the robustness of cooperation in spatial settings. However, one assumption we did not change was the decision rule (aka update rule). Roca et al. (2009a, 2009b) conducted an impressive simulation study of the effect of spatial structure in 2×2 games, and discovered that the decision rule can play a major role. In particular, they found that the imitate the best neighbor rule (which Roca et al. (2009a, 2009b) call “unconditional imitation”) favors cooperation in the Prisoner’s Dilemma more than any other decision rule they studied.
In what concerns the Prisoner’s Dilemma, the above results also prove that the promotion of cooperation in this game is not robust against changes in the update rule, because the beneficial effect of spatial lattices practically disappears for rules different from unconditional imitation, when seen in the wider scope of the ST plane. Roca et al. (2009b, p. 9)
In this chapter we are going to implement several decision rules. This will allow us to replicate Roca et al.’s (2009a, 2009b) results… and many others (see the proposed exercises).
3. Description of the model
The model we are going to develop here is a generalization of the model implemented in the previous chapter. In particular, we are going to add the following four parameters:
- neighborhood-type. This parameter is used to define the agents’ neighborhood (both for playing and for strategy updating).[2] The parameter can have two possible values: “Moore” for a Moore neighborhood, or “Von Neumann” for a Von Neumann neighborhood.
- neighborhood-range. This parameter determines the range of the neighborhood. A patch’s Moore neighborhood of range r consists of the patches within Chebyshev distance r. A patch’s Von Neumann neighborhood of range r is composed of the patches within Manhattan distance r. Note that in our descriptions of decision rules below, we do not consider a patch to be a neighbor of itself unless otherwise stated.
- decision-rule. This parameter determines the decision rule that agents will follow. It will be implemented with a chooser, with five possible values:
- “best-neighbor” (Nowak and May, 1992, 1993). This is the imitate the best neighbor rule, already implemented in our model.[3]
- “imitate-if-better-all-nbrs“. This is the imitate if better rule (Izquierdo and Izquierdo, 2013; Loginov, 2021) adapted to networks, where agents play with all their neighbors. Under this rule, the revising agent looks at a random neighbor and copies her strategy if and only if the observed neighbor’s average payoff is higher than the revising agent’s average payoff.
- “imitative-pairwise-difference” (Hauert, 2002,[4] 2006). This is the imitative pairwise-difference rule we saw in chapter I-2 adapted to networks. Under this rule, the revising agent looks at a random neighbor and considers copying her strategy only if the observed neighbor’s average payoff is higher than the revising agent’s average payoff; in that case, the revising agent switches with probability proportional to the payoff difference.[5]
- “imitative-positive-proportional-m” (Nowak et al., 1994a, b). Under this decision rule, the revising agent copies the strategy of one of her neighbors (including herself, in this case), selected with probability proportional to their total payoff raised to parameter m.[6] Parameter m controls the intensity of selection (see below). We do not allow for negative payoffs when using this rule.[7]
- “Fermi-m” (Szabó and Tőke, 1998; Traulsen and Hauert, 2009; Roca et al. 2009a, 2009b; Perc and Szolnoki, 2010, Adami et al., 2016). Under this decision rule, the revising agent
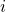 looks at one of her neighbors
looks at one of her neighbors 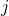 at random and copies her strategy with probability
at random and copies her strategy with probability 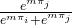 , where
, where 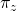 denotes agent
denotes agent  ‘s average payoff and
‘s average payoff and 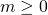 .[8] Parameter m controls the intensity of selection (see below).
.[8] Parameter m controls the intensity of selection (see below).
- m. This is a parameter that controls the intensity of selection in decision rules imitative-positive-proportional-m and Fermi-m (see above). High values of m imply that selection is strongly based on payoffs, i.e. the agents with the highest payoffs will be chosen with very high probability. Lower values of m mean that the sensitivity of selection to payoffs is weak (e.g. if m = 0, selection among agents is random, i.e. independent of their payoffs).
Everything else stays as described in the previous chapter.
 4. Interface design
4. Interface design
We depart from the model we developed in the previous chapter (so if you want to preserve it, now is a good time to duplicate it).
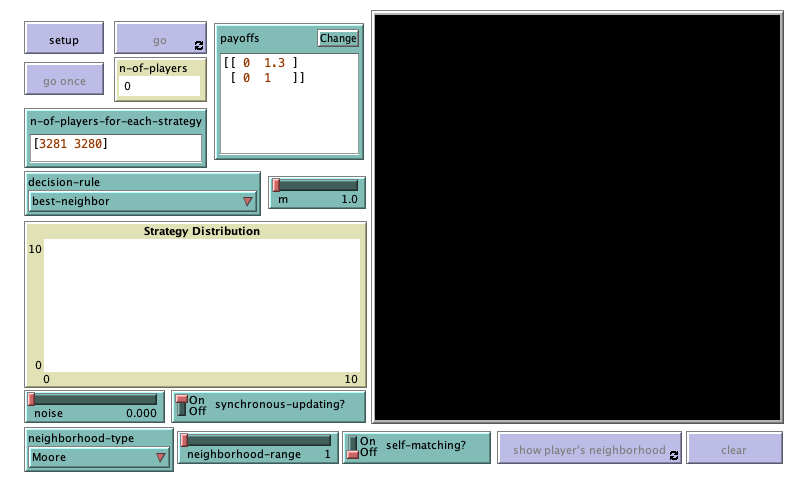
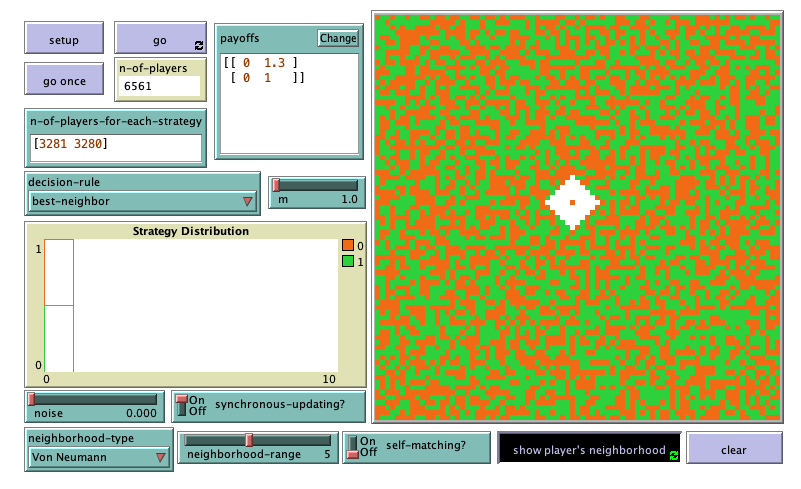
In the new interface (see figure 1 above), we have to add:
- One chooser for new parameter neighborhood-type (with possible values “Moore” and “Von Neumann“), and a slider for parameter neighborhood-range (with minimum = 1 and increment = 1).
- One chooser for new parameter decision-rule (with possible values “best-neighbor“, “imitate-if-better-all-nbrs“, “imitative-pairwise-difference“, “imitative-positive-proportional-m” and “Fermi-m“), and a slider for parameter m (with minimum = 0 and increment = 0.1).
We have also added a button (labeled ) to see any patch’s neighborhood on the 2D view and another button (labeled ) to clear the display of the neighborhood.
 5. Code
5. Code
5.1. Skeleton of the code
The skeleton of the code for procedures to setup and to go is the same as in the previous model. In this chapter we will modify mainly the following two procedures:
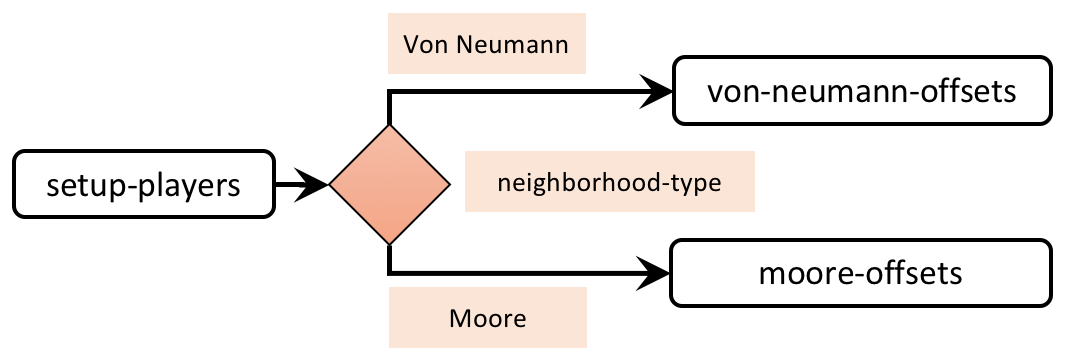
- procedure to setup-players, to set the players’ neighborhoods according to parameters neighborhood-type and neighborhood-range (see figure 2).
- procedure to update-strategy-after-revision, to run the decision rule indicated in parameter decision-rule (see figure 3).
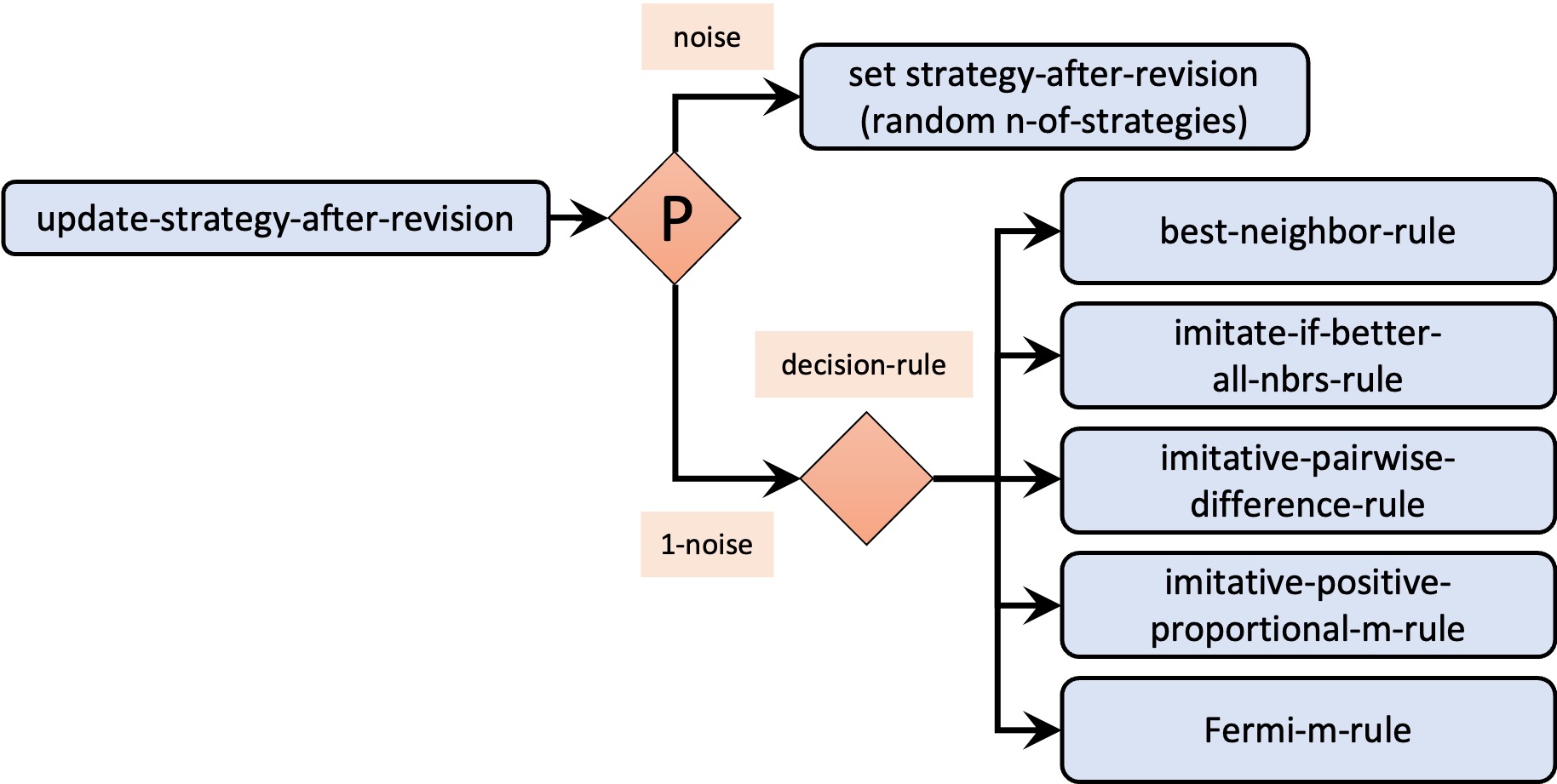
Figure 3. Calls to other procedures from procedure to update-strategy-after-revision
5.2. Extension I. Implementation of different neighborhoods
Recall that patches have the following two individually owned variables:
- my-coplayers, which contains the set of agents with whom the patch plays the game (and is affected by parameter self-matching?), and
- my-nbrs-and-me, which is the set of agents the player considers when revising its strategy.
These two agentsets are the same if self-matching? is true, and differ only in the focal patch if self-matching? is false. We will keep this distinction for any type of neighborhood.
To implement the different neighborhoods, primitive at-points will be very useful. This primitive reports a subset of a given agentset that includes only the agents on the patches at the given coordinates (relative to the calling agent). As an example, the following code gives a patch’s Von Neumann neighborhood of range 1 (including the patch itself):
patches at-points [[-1 0] [0 -1] [0 0] [0 1] [1 0]]
And the following code gives a patch’s Moore neighborhood of range 1 (including the patch itself):
patches at-points [[-1 -1] [-1 0] [-1 1] [0 -1] [0 0] [0 1] [1 -1] [1 0] [1 1]]
Thus, the key is to implement procedures that report the appropriate lists of relative coordinates.[9] Let’s do this!
Implementation of relative coordinates for Moore neighborhoods
Our goal here is to implement a procedure that reports the appropriate list of relative coordinates for Moore neighborhoods, for any given range and letting the user choose whether the list should include the item [0 0] or not. Let us call this reporter to-report moore-offsets. Note that this reporter takes two inputs, which we can call r (for range) and include-center?.
to-report moore-offsets [r include-center?] ;; code to be written end
Below we provide some examples of what reporter to-report moore-offsets should produce:
- If r = 1 and include-center? is true:
[[-1 -1] [-1 0] [-1 1] [0 -1] [0 0] [0 1] [1 -1] [1 0] [1 1]]
- If r = 1 and include-center? is false:
[[-1 -1] [-1 0] [-1 1] [0 -1] [0 1] [1 -1] [1 0] [1 1]]
- If r = 2 and include-center? is true:
[[-2 -2] [-2 -1] [-2 0] [-2 1] [-2 2] [-1 -2] [-1 -1] [-1 0] [-1 1] [-1 2] [0 -2] [0 -1] [0 0] [0 1] [0 2] [1 -2] [1 -1] [1 0] [1 1] [1 2] [2 -2] [2 -1] [2 0] [2 1] [2 2]]
Note that the effect of input include-center? is just to include or exclude [0 0] from the output list, so we can worry about that at the end of the implementation. To produce the list of Moore offsets for range r, we can start building the list l = [ –r, –r+1, …, r-1, r ] and then build 2-item lists with each element of the list l together with each element of the same list l. Thus, let us build the list l = [ –r, –r+1, …, r-1, r ]:
let l (range (- r) (r + 1))
To build 2-items lists with first element el1 and second element each of the elements of list l, we can use primitive map as follows:
map [el2 -> list el1 el2] l
And now we should make el1 be each of the elements of list l. For this we can use primitive map again:
map [ el1 -> map [el2 -> list el1 el2] l] l
The only problem now is that we have several nested lists. For example, the code above for l = [ -1, 0, 1 ] produces:
[[[-1 -1] [-1 0] [-1 1]] [[0 -1] [0 0] [0 1]] [[1 -1] [1 0] [1 1]]]
Note that the outmost list contains three sublists, each of which contains three 2-item lists. We can get rid of the extra lists using primitives reduce and sentence:
let result reduce sentence map [ el1 -> map [el2 -> list el1 el2] l] l
The code above creates the list of required offsets, including [0 0]. Now we just have to remove [0 0] if and only if input include-center? is false. Thus, the final code for reporter to-report moore-offsets is as follows:
to-report moore-offsets [r include-center?] let l (range (- r) (r + 1)) let result reduce sentence map [ el1 -> map [el2 -> list el1 el2] l] l report ifelse-value include-center? [ result ] [ remove [0 0] result ] end
Implementation of relative coordinates for Von Neumann neighborhoods
Our goal here is to implement a procedure that reports the appropriate list of relative coordinates for Von Neumann neighborhoods. Let us call this reporter to-report von-neumann-offsets and let us call its inputs r (for range) and include-center?, just like before.
to-report von-neumann-offsets [r include-center?] ;; code to be written end
Note that, for any given r and include-center?, the list of offsets for a Von Neumann neighborhood is a subset of the list of offsets for the corresponding Moore neighborhood. In particular, the list of Von Neumann offsets is composed of the elements [el1 el2] in the list of Moore offsets that satisfy the condition |el1| + |el2| ≤ r . Thus, we can create the corresponding list of Moore offsets and filter those coordinates that satisfy the condition using primitive filter. Do you want to give it a try?
Implementation of procedure to-report von-neumann-offsets
Yes, well done!
to-report von-neumann-offsets [r include-center?] let moore-list (moore-offsets r include-center?) report filter [l -> abs first l + abs last l <= r] moore-list end
Putting everything together
Now that we have implemented to-report moore-offsets and to-report von-neumann-offsets, we can use them in procedure to setup-players to create the right neighborhood for each patch. The only lines we have to modify are the ones highlighted in bold below:
to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ]
if sum initial-distribution != count patches [ user-message (word "The total number of agents in\n" "n-of-agents-for-each-strategy (i.e. " sum initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of patches (i.e. " count patches ")" ) ]
ask patches [set strategy false] let i 0 let offsets ifelse-value (neighborhood-type = "Von Neumann") [ von-neumann-offsets neighborhood-range self-matching? ] [ moore-offsets neighborhood-range self-matching? ]
foreach initial-distribution [ j -> ask n-of j (patches with [strategy = false]) [ set payoff 0 set strategy i set strategy-after-revision strategy set my-coplayers patches at-points offsets set n-of-my-coplayers (count my-coplayers) set my-nbrs-and-me (patch-set my-coplayers self) ] set i (i + 1) ]
set n-of-players count patches end
Note that variable my-coplayers may or may not contain the patch itself (depending on the value of parameter self-matching?), but variable my-nbrs-and-me will always contain it, since we are setting its value to (patch-set my-coplayers self). This is perfectly fine even if my-coplayers already contains the patch itself, since agentsets do not contain duplicates. Adding an agent a to an agentset that already contains that agent a has no effect whatsoever.[10]
A nice final touch
Finally, we are going to write some code to let the user see the neighborhood of any patch in the 2D view by clicking on it. This is just for displaying purposes, so feel free to skip this if you’re not really interested. Let us start by implementing a new procedure called to show-neighborhood as follows:
to show-neighborhood if mouse-down? [ ask patch mouse-xcor mouse-ycor [ ask my-coplayers [set pcolor white] ] ] display end
You may want to read the documentation for primitives mouse-down?, mouse-xcor and mouse-ycor. Basically, this procedure paints in white the patches contained in the variable my-coplayers of the patch you click with your mouse. However, for this to work, the procedure must be running all the time. To do this, we can run this procedure within the button labeled in the interface, and make this button be a “forever” button.
Insert the following code within the button labeled :
with-local-randomness [show-neighborhood]
The use of primitive with-local-randomness guarantees that this piece of code does not interfere with the generation of pseudorandom numbers for the rest of the model.
To clear the white paint, insert the following code within the button labeled (which should not be a “forever” button):
with-local-randomness [ ask patches [update-color] ]
Figure 4 shows a patch’s Von Neumann neighborhood of range 5 (excluding the patch itself) painted in white.
5.3. Extension II. Implementation of different decision rules
The implementation of the decision rule takes place in procedure to update-strategy-after-revision. Note that the effect of noise is the same regardless of the decision rule, so we can deal with noise in a unified way, regardless of which decision rule will be executed. One possible way of doing this is as follows:
to update-strategy-after-revision ifelse (random-float 1 < noise) [ set strategy-after-revision random n-of-strategies ] [ ;; code to set strategy-after-revision ;; using the decision rule indicated by the user ;; through parameter decision-rule ] end
To make the implementation of decision rules elegant and modular, we should implement a different procedure for each decision rule. Let us call these procedures: best-neighbor-rule, imitate-if-better-all-nbrs-rule, imitative-pairwise-difference-rule, imitative-positive-proportional-m-rule and Fermi-m-rule. With these procedures in place, the code for procedure to update-strategy-after-revision would just look as follows:
to update-strategy-after-revision ifelse (random-float 1 < noise) [ set strategy-after-revision random n-of-strategies ] [ (ifelse decision-rule = "best-neighbor" [ best-neighbor-rule ] decision-rule = "imitate-if-better-all-nbrs" [ imitate-if-better-all-nbrs-rule ] decision-rule = "imitative-pairwise-difference" [ imitative-pairwise-difference-rule ] decision-rule = "imitative-positive-proportional-m" [ imitative-positive-proportional-m-rule ] decision-rule = "Fermi-m" [ Fermi-m-rule ] ) ] end
Note that primitive ifelse can work with multiple conditions, just like switch statements in other programming languages.[11]
Now we just have to implement the procedures for each of the four decision rules. Do you want to give it a try? The first one is not very difficult.
Implementation of procedure to best-neighbor-rule
to best-neighbor-rule set strategy-after-revision [strategy] of one-of my-nbrs-and-me with-max [payoff] end
Implementing procedure to imitate-if-better-all-nbrs-rule is slightly more difficult, but we believe you can do it. Remember that players consider average payoffs, rather than total payoffs.
Implementation of procedure to imitate-if-better-all-nbrs-rule
to imitate-if-better-all-nbrs-rule let observed-player one-of other my-coplayers if ([payoff / n-of-my-coplayers] of observed-player) > (payoff / n-of-my-coplayers) [ set strategy-after-revision ([strategy] of observed-player) ] end
The implementation of procedure to imitative-pairwise-difference-rule is significantly more difficult than the previous one, but if you have managed to read this book until here, you certainly have what it takes to do it!
Implementation of procedure to imitative-pairwise-difference-rule
A possible implementation of this procedure is as follows:
to imitative-pairwise-difference-rule let observed-player one-of other my-coplayers
;; compute difference in average payoffs let payoff-diff ([payoff / n-of-my-coplayers] of observed-player - (payoff / n-of-my-coplayers))
set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / max-payoff-difference)) [ [strategy] of observed-player ] [ strategy ] ;; If your strategy is the better, payoff-diff is negative, ;; so you are going to stick with it. ;; If it's not, you switch with probability ;; (payoff-diff / max-payoff-difference) end
Note that we are using a new variable, i.e. max-payoff-difference, to make sure that the agent changes strategy with probability proportional to the average payoff difference. Thus, we should define it as global (since this max-payoff difference will not change over the course of a run), as follows:
globals [ payoff-matrix n-of-strategies n-of-players max-payoff-difference ;; <== New line ]
We also have to set the value of this new variable. We can do that at the end of the setup-payoffs method, as follows:
to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix
;; new lines below set max-payoff-difference (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) end
Finally, note that we have implemented two new procedures to compute the minimum and the maximum value of a matrix:
;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; SUPPORTING PROCEDURES ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;; ;;; Matrices ;;; ;;;;;;;;;;;;;;;; to-report max-of-matrix [matrix] report max reduce sentence matrix end to-report min-of-matrix [matrix] report min reduce sentence matrix end
To implement procedure to imitative-positive-proportional-m-rule, there is an extension that comes bundled with NetLogo which will make our life much easier: extension rnd. To use it, you just have to add the following line at the beginning of your code
extensions [rnd]
Having loaded the rnd extension, you can use primitive rnd:weighted-one-of, which will be very handy. With this information, you may want to try to implement this short procedure yourself.
Implementation of procedure to imitative-positive-proportional-m-rule
to imitative-positive-proportional-m-rule let chosen-nbr rnd:weighted-one-of my-nbrs-and-me [ payoff ^ m ] set strategy-after-revision [strategy] of chosen-nbr end
If you wanted to use average rather than total payoffs, you would only have to divide the payoff by n-of-my-coplayers.
To avoid errors when payoffs are negative and this rule is used, it would be nice to check that payoffs are non-negative, and if they are, let the user know. We can do this implementing the following procedure:
to check-payoffs-are-non-negative if min reduce sentence payoff-matrix < 0 [ user-message (word "Since you are using decision-rule =\n" "imitative-positive-proportional-m,\n" "all elements in the payoff matrix\n" payoffs "\nshould be non-negative numbers.") ] end
An appropriate place to call this procedure would be at the end of procedure to setup-payoffs, which would then be as follows:
to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix
;; New lines below set max-payoff-difference (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) if decision-rule = "imitative-positive-proportional-m" [ check-payoffs-are-non-negative ] end
The implementation of procedure to Fermi-m-rule is not extremely hard after having seen the implementation of to imitative-pairwise-difference-rule, and realizing that ![]() .
.
Implementation of procedure to Fermi-m-rule
A possible implementation of this procedure is as follows:
to Fermi-m-rule let observed-player one-of other my-coplayers
;; compute difference in average payoffs
let payoff-diff ([payoff / n-of-my-coplayers] of observed-player
- (payoff / n-of-my-coplayers))
set strategy-after-revision ifelse-value (random-float 1 < (1 / (1 + exp (- m * payoff-diff)))) [ [strategy] of observed-player ] [ strategy ] end
5.4. Complete code in the Code tab
The Code tab is ready! Congratulations! With this model you can rigorously explore the effect of space in 2-player games.
extensions [rnd] ;; <== New line globals [ payoff-matrix n-of-strategies n-of-players max-payoff-difference ;; <== New line ] patches-own [ strategy strategy-after-revision payoff my-nbrs-and-me my-coplayers n-of-my-coplayers ] to setup clear-all setup-payoffs setup-players setup-graph reset-ticks update-graph ask patches [update-color] end to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix
;; New lines below set max-payoff-difference (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) if decision-rule = "imitative-positive-proportional-m" [ check-payoffs-are-non-negative ] end to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ]
if sum initial-distribution != count patches [ user-message (word "The total number of agents in\n" "n-of-agents-for-each-strategy (i.e. " sum initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of patches (i.e. " count patches ")" ) ]
ask patches [set strategy false] let i 0 let offsets ifelse-value (neighborhood-type = "Von Neumann") [ von-neumann-offsets neighborhood-range self-matching? ] [ moore-offsets neighborhood-range self-matching? ]
foreach initial-distribution [ j -> ask n-of j (patches with [strategy = false]) [ set payoff 0 set strategy i set strategy-after-revision strategy set my-coplayers patches at-points offsets set n-of-my-coplayers (count my-coplayers) set my-nbrs-and-me (patch-set my-coplayers self) ] set i (i + 1) ]
set n-of-players count patches end to setup-graph set-current-plot "Strategy Distribution" foreach (range n-of-strategies) [ i -> create-temporary-plot-pen (word i) set-plot-pen-mode 1 set-plot-pen-color 25 + 40 * i ] end to go ifelse synchronous-updating? [ ask patches [ play ] ask patches [ update-strategy-after-revision ] ;; here we are not updating the agent's strategy yet ask patches [ update-strategy ] ;; now we update every agent's strategy at the same time ] [ ask patches [ play ask my-coplayers [ play ] ;; since your coplayers' strategies or ;; your coplayers' coplayers' strategies ;; could have changed since the last time ;; your coplayers played update-strategy-after-revision update-strategy ] ] tick update-graph ask patches [update-color] end to play let n-of-coplayers-with-strategy-? n-values n-of-strategies [ i -> count my-coplayers with [strategy = i] ] let my-payoffs (item strategy payoff-matrix) set payoff sum (map * my-payoffs n-of-coplayers-with-strategy-?) end to update-strategy-after-revision ifelse (random-float 1 < noise) [ set strategy-after-revision random n-of-strategies ] [ (ifelse decision-rule = "best-neighbor" [ best-neighbor-rule ] decision-rule = "imitate-if-better-all-nbrs" [ imitate-if-better-all-nbrs-rule ] decision-rule = "imitative-pairwise-difference" [ imitative-pairwise-difference-rule ] decision-rule = "imitative-positive-proportional-m" [ imitative-positive-proportional-m-rule ] decision-rule = "Fermi-m" [ Fermi-m-rule ] ) ] end to best-neighbor-rule set strategy-after-revision [strategy] of one-of my-nbrs-and-me with-max [payoff] end
to imitate-if-better-all-nbrs-rule let observed-player one-of other my-coplayers
if ([payoff / n-of-my-coplayers] of observed-player) > (payoff / n-of-my-coplayers) [ set strategy-after-revision ([strategy] of observed-player) ] end
to imitative-pairwise-difference-rule let observed-player one-of other my-coplayers
;; compute difference in average payoffs let payoff-diff ([payoff / n-of-my-coplayers] of observed-player - (payoff / n-of-my-coplayers))
set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / max-payoff-difference)) [ [strategy] of observed-player ] [ strategy ] ;; If your strategy is the better, payoff-diff is negative, ;; so you are going to stick with it. ;; If it's not, you switch with probability ;; (payoff-diff / max-payoff-difference) end to imitative-positive-proportional-m-rule let chosen-nbr rnd:weighted-one-of my-nbrs-and-me [ payoff ^ m ] ;; https://ccl.northwestern.edu/netlogo/docs/rnd.html#rnd:weighted-one-of set strategy-after-revision [strategy] of chosen-nbr end to Fermi-m-rule let observed-player one-of other my-coplayers
;; compute difference in average payoffs let payoff-diff ([payoff / n-of-my-coplayers] of observed-player - (payoff / n-of-my-coplayers))
set strategy-after-revision ifelse-value (random-float 1 < (1 / (1 + exp (- m * payoff-diff)))) [ [strategy] of observed-player ] [ strategy ] end to update-strategy set strategy strategy-after-revision end to update-graph let strategy-numbers (range n-of-strategies) let strategy-frequencies map [ n -> count patches with [strategy = n] / n-of-players ] strategy-numbers
set-current-plot "Strategy Distribution" let bar 1 foreach strategy-numbers [ n -> set-current-plot-pen (word n) plotxy ticks bar set bar (bar - (item n strategy-frequencies)) ] set-plot-y-range 0 1 end to update-color set pcolor 25 + 40 * strategy end ;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; SUPPORTING PROCEDURES ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;; to-report moore-offsets [r include-center?] let l (range (- r) (r + 1)) let result reduce sentence map [ el1 -> map [el2 -> list el1 el2] l] l report ifelse-value include-center? [ result ] [ remove [0 0] result ] end to-report von-neumann-offsets [r include-center?] let moore-list (moore-offsets r include-center?) report filter [l -> abs first l + abs last l <= r] moore-list end to show-neighborhood if mouse-down? [ ask patch mouse-xcor mouse-ycor [ ask my-coplayers [set pcolor white] ] ] display end to check-payoffs-are-non-negative if min reduce sentence payoff-matrix < 0 [ user-message (word "Since you are using decision-rule =\n" "imitative-positive-proportional-m,\n" "all elements in the payoff matrix\n" payoffs "\nshould be non-negative numbers.") ] end ;;;;;;;;;;;;;;;; ;;; Matrices ;;; ;;;;;;;;;;;;;;;; to-report max-of-matrix [matrix] report max reduce sentence matrix end to-report min-of-matrix [matrix] report min reduce sentence matrix end
6. Sample runs
6.1. Decision rules
Now that we have implemented the model, we can explore the impact of the decision rule on the promotion of cooperation in the spatially embedded Prisoner’s Dilemma. Let us explore this question using the parameter values shown in figure 1 above. We start with the imitate the best neighbor rule. The simulation below shows a representative run.
As you can see in the video above, with the imitate the best neighbor rule, high levels of cooperation are achieved (i.e. about 90% of the patches cooperate in the long run). But, how robust is this result to changes in the decision rule? To explore this question, let us run the same simulation with the other four decision rules we have implemented. The simulation below shows a representative run with the imitate-if-better-all-nbrs rule.
As you can see in the video, with the imitate-if-better-all-nbrs rule there is no cooperation at all. Defection takes over in about forty ticks. Let us see what happens with the imitative-pairwise-difference rule.
With the imitative-pairwise-difference rule, again, there is no cooperation at all in the long run. Let us now try the imitative-positive-proportional-m rule with m = 1:[12]
We do not observe any cooperation at all with the imitative-positive-proportional-m rule (with m = 1) either. Finally, let us try the Fermi-m rule with m = 1 (or any other positive value, for that matter):[13]
And we observe universal defection again! Clearly, as Roca et al. (2009a, 2009b) point out, the imitate the best neighbor rule seems to favor cooperation in the Prisoner’s Dilemma more than other decision rules.
6.2. Neighborhoods
What about if we change the type of neighborhood? You can check that the simulations shown in the videos above do not change qualitatively if we use Von Neumann neighborhoods rather than Moore neighborhoods. However, what does make a difference is the size of the neighborhood. Note that if the size is so large that agents’ neighborhoods encompass the whole population, we have a global interaction model (i.e. a model without population structure). Thus, the size of the neighborhood allows us to study the effect of population structure in a gradual manner. Having seen this, we can predict that, for the imitate the best neighbor rule, if we increase the size of the neighborhood enough, at some point cooperation will disappear. As an exercise, try to find the minimum neighborhood-range (for both types of neighborhood) at which cooperation cannot be sustained anymore, with the other parameter values as shown in figure 1.
Critical neighborhood size at which cooperation does not emerge in the simulation parameterized as in figure 1.
- neighborhood-type = “Moore“. With neighborhood-range = 1, we observe significant levels of cooperation (about 90%) cooperation, but with neighborhood-range ≥ 2, we observe no cooperation at all.
- neighborhood-type = “Von Neumann“. With neighborhood-range = 1, we observe significant levels of cooperation (about 75%) cooperation. Interestingly, with neighborhood-range = 2, we observe even more cooperation (usually more than 90%), but with neighborhood-range ≥ 3, we observe no cooperation at all.
6.3. Discussion
We would like to conclude this chapter emphasizing that the influence of population structure on evolutionary dynamics generally depends on many factors that may seem insignificant at first sight, and whose effects interact in complex ways. This may sound discouraging, since it suggests that a simple general theory of the influence of population structure on evolutionary dynamics cannot be derived. On a more positive note, it also highlights the importance of the skills you are learning with this book. Without the aid of computer simulation, it seems impossible to explore this type of questions. But using computer simulation we can gain some understanding of the complexity and the beauty of these apparently simple –yet surprisingly intricate– systems. The following quote from Roca et al. (2009b) nicely summarizes this view.
To conclude, we must recognize the strong dependence on details of evolutionary games on spatial networks. As a consequence, it does not seem plausible to expect general laws that could be applied in a wide range of practical settings. On the contrary, a close modeling including the kind of game, the evolutionary dynamics and the population structure of the concrete problem seems mandatory to reach sound and compelling conclusions. With no doubt this is an enormous challenge, but we believe that this is one of the most promising paths that the community working in the field can explore. Roca et al. (2009b, pp. 14-15)
7. Exercises
You can use the following link to download the complete NetLogo model: nxn-imitate-best-nbr-extended.nlogo.

Exercise 1. How can we parameterize our model to replicate the results shown in figures 1b and 1d of Hauert and Doebeli (2004)?
Exercise 2. How can we parameterize our model to replicate the results shown in figures 1, 2, 6 and 7 of Nowak et al. (1994a)?[14]
Exercise 3. How can we parameterize our model to replicate the results shown in figure 1 of Szabó and Tőke (1998)? Note that Szabó and Tőke (1998) use total payoffs and we use average payoffs in our Fermi-m rule, but a clever parameterization can save you any programming efforts.
Exercise 4. How can we parameterize our model to replicate the results shown in figure 11 of Nowak and May (1993)?
Exercise 5. To appreciate the impact that neighborhood-type may have, run a simulation parameterized as in figure 1 above, but with decision-rule = “Fermi-m”, m = 10, and self-matching? = true. Compare the results obtained using neighborhood-type = “Moore” and neighborhood-type = “Von Neumann”. What do you observe?
![]() Exercise 6. The following block of code (in procedure to update-strategy-after-revision) can be replaced by one simple line using run (a primitive that can take a string containing the name of a command as an input, and it runs the command).
Exercise 6. The following block of code (in procedure to update-strategy-after-revision) can be replaced by one simple line using run (a primitive that can take a string containing the name of a command as an input, and it runs the command).
[ (ifelse decision-rule = "best-neighbor" [ best-neighbor-rule ] decision-rule = "imitate-if-better-all-nbrs" [ imitate-if-better-all-nbrs-rule ] decision-rule = "imitative-pairwise-difference" [ imitative-pairwise-difference-rule ] decision-rule = "imitative-positive-proportional-m" [ imitative-positive-proportional-m-rule ] decision-rule = "Fermi-m" [ Fermi-m-rule ] ) ]
Can you come up with the simple line?
- The names given to the different rules follow Izquierdo et al. (2019). ↵
- Recall that the set of patches that a patch plays with also depends on the value of self-matching?. ↵
- Roca et al. (2009a, 2009b) call this decision rule "unconditional imitation" and Hauert (2002) calls it "best takes over". Also, note that Hauert (2002) resolves ties differently. ↵
- See Roca et al. (2009b) for an important and illuminating discussion of this paper. ↵
- Roca et al. (2009a, 2009b) call this decision rule "replicator rule" or "proportional imitation rule", though their implementation is not exactly the same as ours. They use total payoffs and we use average payoffs. The two implementations differ only if it is possible that two agents have different number of neighbors (e.g. as with non-periodic boundary conditions). Note, however, that Roca et al. (2009a, 2009b)'s experiments have periodic boundary conditions, i.e. all agents have the same number of neighbors, so for all these cases the two implementations are equivalent. Hauert (2002) calls this decision rule "imitate the better". ↵
- It may make more sense to use average rather than total payoffs. We use total payoffs here to be able to replicate Nowak et al.'s (1994a, b) experiments. To use average payoffs, the change in the code is minimal. ↵
- Roca et al. (2009a, 2009b) call this decision rule with m = 1 "Moran rule". Their implementation is not exactly the same as ours, since they do allow for negative payoffs by introducing a constant. Note, however, that the two implementations are equivalent if payoffs are non-negative. Hauert (2002) calls this decision rule with m = 1 "proportional update". ↵
- Note that some authors (e.g. Szabó and Tőke, 1998) use total payoffs rather than average payoffs. ↵
- Our implementation is heavily based on code example titled "Moore & Von Neumann Example", which you can find in NetLogo models library. Note, however, that this code example does not compute the correct neighborhoods if the center of the world lies at the edge or at a corner of the world (at least in version 6.4.0 and previous ones). ↵
- For instance, the following code reports true.
show (patch-set patch 0 0 patch 0 0) = (patch-set patch 0 0)
↵ - This functionality was added in NetLogo 6.1. ↵
- As long as m ≤ 5, results are very similar, but for greater values of m (i.e. greater intensity of selection) cooperation starts to emerge. ↵
- In contrast with what happens under the imitative-positive-proportional-m rule, parameter m does not seem to have a great influence in this case. This changes if self-matching? is turned on. In that case, for high values of m, cooperation can emerge. ↵
- Figures 1 and 2 in Nowak et al. (1994a) are the same as figures 1 and 2 in Nowak et al. (1994b). ↵