Part IV. Games on networks
IV-4. Other ways of computing payoffs and other decision rules
1. Goal
Our goal in this chapter is to extend the model we have created in the previous chapter by adding two features that can have a major impact on the dynamics of evolutionary models run on networks:
- The possibility to model different ways of computing payoffs. In our current model, agents obtain their payoffs by playing with one of their neighbors, chosen at random. This means that every agent obtains just one payoff, regardless of their network degree. In this chapter we will allow for the possibility that agents play with all their neighbors. When agents play with all their neighbors, they may consider the average payoff or, alternatively, the total (accumulated) payoff.
- The possibility to model other decision rules besides the imitate if better rule. In particular, we will implement all the decision rules we implemented in chapter III-4 for games played on grids.
2. Motivation. Cooperation on scale-free networks
In a series of highly-cited papers, Santos, Pacheco and colleagues (Santos and Pacheco (2005, 2006); Santos et al. (2006a, 2006b)) showed that scale-free networks can greatly promote cooperation in the Prisoner’s Dilemma (figure 1).
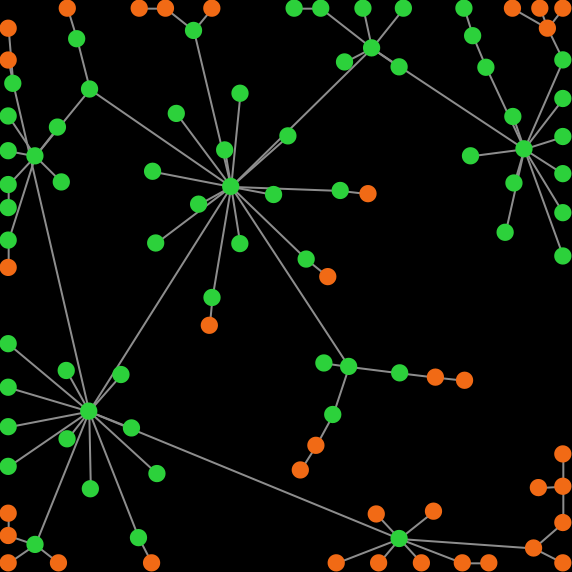
In their model, agents play with all their neighbors and their payoff is the total (accumulated) payoff over all their interactions in the tick. In this chapter we are going to extend our model so we can replicate some of their results and check their robustness to different factors. Let’s do it!
3. Description of the model
The model we are going to develop here is a generalization of the model implemented in the previous chapter. In particular, we are going to add the following three parameters:
- play-with. This parameter is used to determine how agents’ payoffs are computed in each tick. It will be implemented with a chooser, with three possible values:
- “one-random-nbr“: agents play with one of their neighbors chosen at random.
- “all-nbrs-AVG-payoff“: agents play with all their neighbors and use the average payoff.
- “all-nbrs-TOTAL-payoff“: agents play with all their neighbors and use the total (accumulated) payoff.
- decision-rule. This parameter determines the decision rule that agents will follow to update their strategies, just like in the model we developed in chapter III-4. Note that all decision rules use the agents’ payoffs, and these are computed following the method prescribed by parameter play-with. Parameter decision-rule will be implemented with a chooser, with six possible values:
- “best-neighbor“. This is the imitate the best neighbor rule we implemented in chapter III-4.
- “imitate-if-better“. This is the imitate if better rule adapted to networks.
- “imitative-pairwise-difference“. This is the imitative pairwise-difference rule implemented in chapter III-4.
- “imitative-positive-proportional-m“. This is the imitative-positive-proportional-m rule implemented in chapter III-4.
- “Fermi-m“. This is the Fermi-m rule implemented in chapter III-4.
- “Santos-Pacheco“. To facilitate the replication of previous results in the literature, we will also implement a variant of the imitative pairwise-difference rule initially proposed by Santos and Pacheco (2005).[1] Under this rule, the revising agent
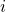 looks at one of her neighbors
looks at one of her neighbors 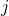 at random and copies her strategy with probability
at random and copies her strategy with probability 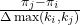 , where
, where 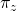 denotes agent
denotes agent  ‘s payoff,
‘s payoff, 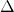 is the maximum payoff difference in the payoff matrix, and
is the maximum payoff difference in the payoff matrix, and 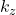 denotes agent
denotes agent  ‘s degree.
‘s degree.
- m. This is the parameter that controls the intensity of selection in decision rules imitative-positive-proportional-m and Fermi-m (see description in chapter III-4).
Everything else stays as described in the previous chapter.
 4. Interface design
4. Interface design
We depart from the model we developed in the previous chapter (so if you want to preserve it, now is a good time to duplicate it).
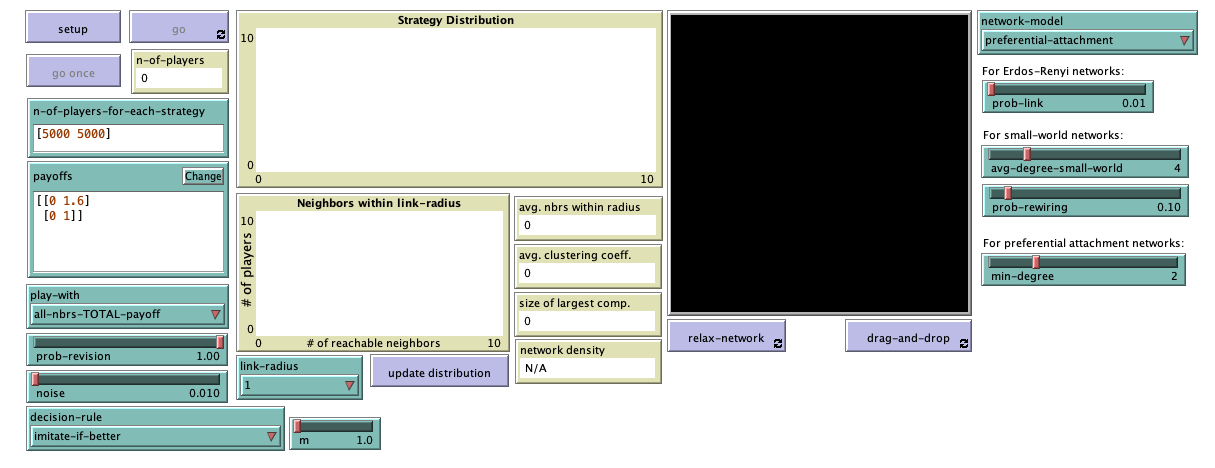
The new interface (see figure 2 above) includes:
- One chooser for new parameter play-with (with possible values “one-random-nbr“, “all-nbrs-AVG-payoff” and “all-nbrs-TOTAL-payoff“).
- One chooser for new parameter decision-rule (with possible values “best-neighbor“, “imitate-if-better“, “imitative-pairwise-difference“, “imitative-positive-proportional-m“, “Fermi-m” and “Santos-Pacheco“).
- A slider for parameter m (with minimum = 0 and increment = 0.1).
 5. Code
5. Code
5.1. Skeleton of the code
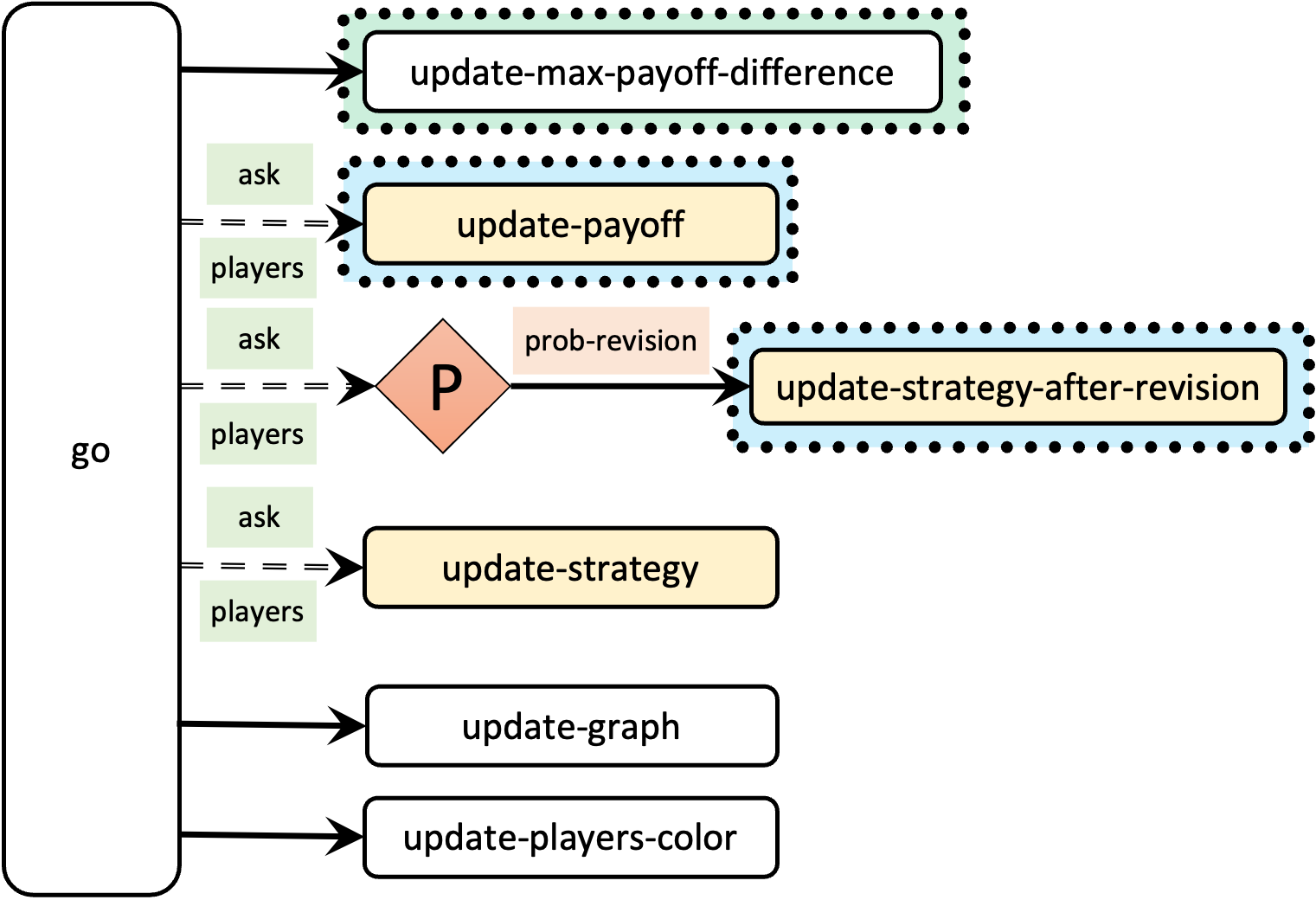
The main changes we will make to our model will take place in procedures to update-payoff and to update-strategy-after-revision. We will also modify other procedures such as to go, to setup-payoffs, and to setup-players, but those changes will be less significant. The skeleton of procedure to go is shown in figure 3.
5.2. Extension I. Different ways of computing payoffs
To implement different ways of computing payoffs, we should modify to update-payoff, so it runs a different procedure depending on the value of parameter play-with, as shown in figure 4.
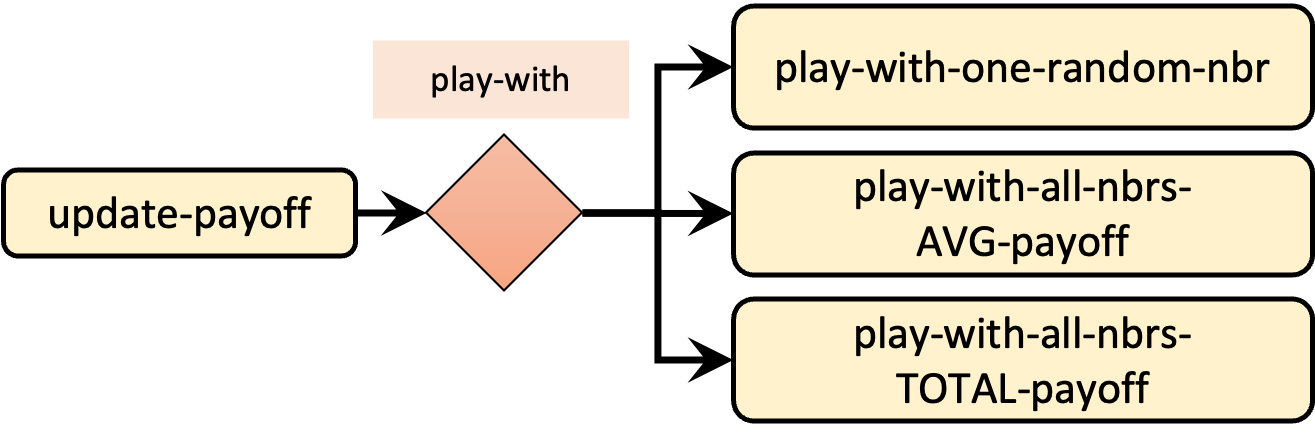
Given the names we have chosen for the new procedures to be implemented (to play-with-one-random-nbr, to play-with-all-nbrs-TOTAL-payoff and to play-with-all-nbrs-AVG-payoff), the new code for procedure to update-payoff is particularly simple:
to update-payoff if any? link-neighbors [ run (word "play-with-" play-with) ] end
To fully understand the code above, note that if the value of parameter play-with is “one-random-nbr“, then the code:
(word "play-with-" play-with)
will report the string “play-with-one-random-nbr”.
Therefore, the code:
run (word "play-with-" play-with)
will run procedure to play-with-one-random-nbr, as desired.
Now we can implement the new payoff-computing procedures. The first one, to play-with-one-random-nbr, is not particularly difficult having seen the previous implementation of to update-payoff. Can you try to do it?
Implementation of procedure to play-with-one-random-nbr
Yes, well done!
to play-with-one-random-nbr let mate one-of link-neighbors set payoff item ([strategy] of mate) (item strategy payoff-matrix) end
Let us now implement to play-with-all-nbrs-TOTAL-payoff. For this one, looking at the implementation of procedure to play in the model we developed in chapter III-4 will be very useful. Note, however, that in our new model we are not going to allow agents to play with themselves, so the variable named my-coplayers will have to be replaced by a Netlogo primitive. Can you give it a try?
Implementation of procedure to play-with-all-nbrs-TOTAL-payoff
Awesome!
to play-with-all-nbrs-TOTAL-payoff let n-of-coplayers-with-strategy-? n-values n-of-strategies [ i -> count link-neighbors with [strategy = i] ] let my-payoffs (item strategy payoff-matrix) set payoff sum (map * my-payoffs n-of-coplayers-with-strategy-?) end
Finally, let us implement to play-with-all-nbrs-AVG-payoff. To do this, it is very tempting to start by copying and pasting the code of procedure to play-with-all-nbrs-TOTAL-payoff but please, don’t do it! Duplicating code is not good practice because it makes the process of detecting and fixing errors much harder, and leads to code that is difficult to read and maintain. Can you implement procedure to play-with-all-nbrs-AVG-payoff without rewriting any of the code written in procedure to play-with-all-nbrs-TOTAL-payoff?
Implementation of procedure to play-with-all-nbrs-AVG-payoff
If you did this correctly, you do deserve a medal right now!
to play-with-all-nbrs-AVG-payoff play-with-all-nbrs-TOTAL-payoff set payoff (payoff / count link-neighbors) end
With this, we have finished the implementation of the first extension to the model.
5.3. Extension II. Different decision rules
The implementation of the decision rule takes place in procedure to update-strategy-after-revision, so we will have to modify its code. Just like we did in chapter III-4, we will make the implementation of decision rules elegant and modular by coding a different procedure for each decision rule and by dealing with noise in a unified way. Figure 5 shows the skeleton of our new procedure to update-strategy-after-revision.
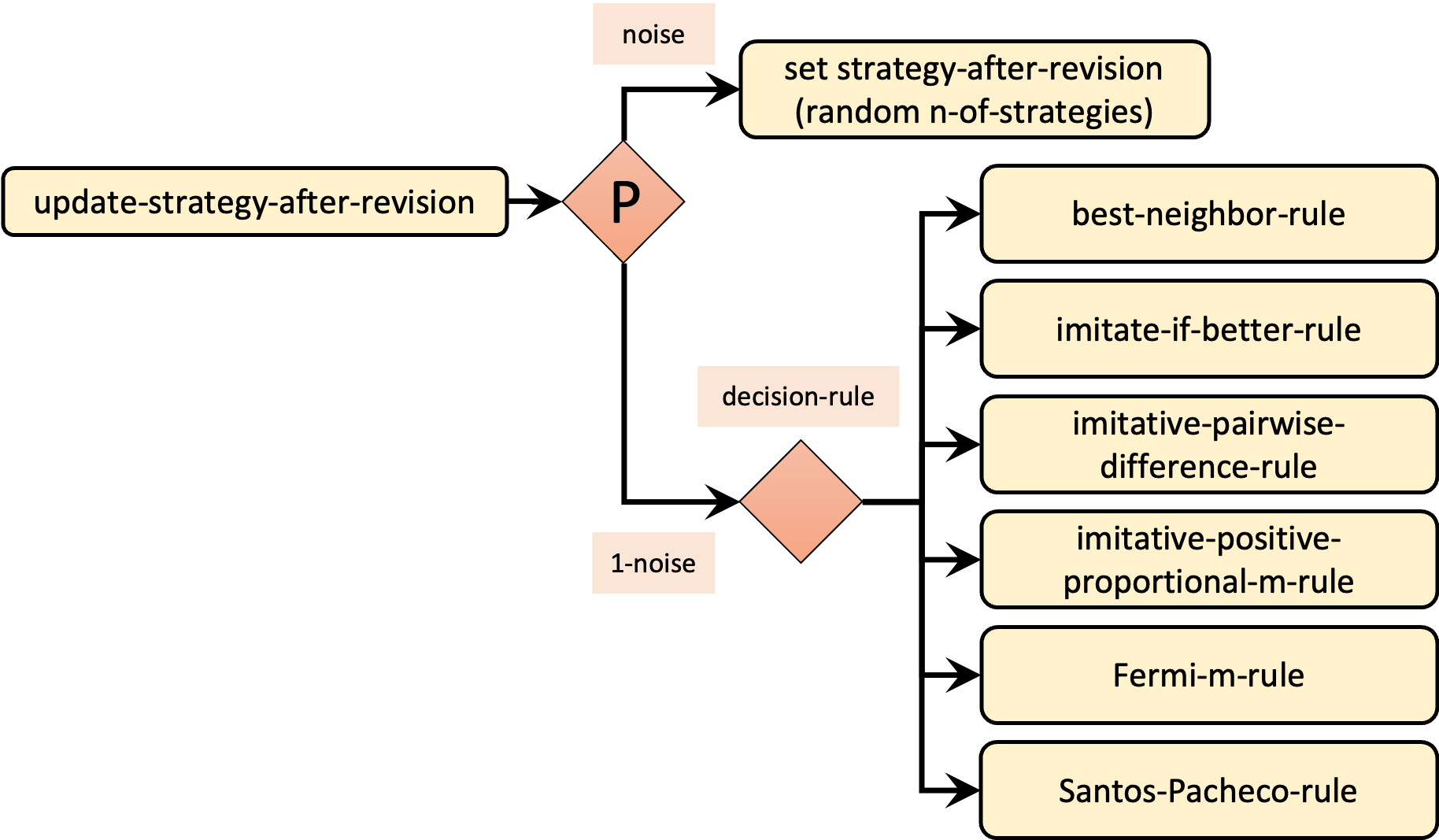
Given the skeleton shown in figure 5 and bearing in mind how we use NetLogo primitive run in our current implementation of procedure to update-payoff, can you venture a simple implementation for our new procedure to update-strategy-after-revision?
Implementation of procedure to update-strategy-after-revision
to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ if any? link-neighbors [run (word decision-rule "-rule")] ] end
Now we just have to implement the procedures for each of the six decision rules. This should be relatively easy given that we have implemented very similar rules in chapter III-4, but we have to keep in mind that:
- now the agents’ payoffs may come in three different flavors, depending on the value of parameter play-with, and
- the set of neighbors in our network model is the set of link-neighbors.
Let us start with procedure to best-neighbor-rule. It will be useful to look at our implementation of this rule for games played on grids. Just like we did in that model, you may want to define a new individually-owned variable named my-nbrs-and-me (and set its value at procedure to setup-players).
Implementation of procedure to best-neighbor-rule
We start by defining the new players-own variable my-nbrs-and-me.
players-own [ strategy strategy-after-revision payoff my-nbrs-and-me ;; <== new line ]
Then, we set its value at procedure to setup-players.
to setup-players ... ifelse n-of-players < 4 [ user-message "There should be at least 4 players" ] [ build-network ask players [set strategy -1] let i 0 foreach initial-distribution [ j -> ask up-to-n-of j players with [strategy = -1] [ set payoff 0 set strategy i set strategy-after-revision strategy set my-nbrs-and-me ;; <== new line (turtle-set link-neighbors self) ;; <== new line ] set i (i + 1) ] set n-of-players count players update-players-color ] end
Once this is done, we can just copy our implementation of this rule for games played on grids.
to best-neighbor-rule set strategy-after-revision [strategy] of one-of my-nbrs-and-me with-max [payoff] end
Note that this code will work correctly no matter how payoffs are computed.
To implement procedure to imitate-if-better-rule, our implementation of procedure to imitate-if-better-all-nbrs-rule for games played on grids will be useful, but we have to keep in mind that the computation of agents’ payoffs is now taken care at procedure to update-payoff, so players-own variable payoff always contains the right value of the payoff (i.e., computed according to the value of parameter play-with).
Implementation of procedure to imitate-if-better-rule
to imitate-if-better-rule let observed-player one-of link-neighbors if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] end
The implementation of procedure to imitative-pairwise-difference-rule is similar to the one we did for games played on grids but we have to bear in mind that the payoff in our model could now come from playing just once or from playing several times. Thus, we will have to think carefully about how to set the value of the maximum payoff difference.
Implementation of procedure to imitative-pairwise-difference-rule
A possible implementation of this procedure is as follows:
to imitative-pairwise-difference-rule let observed-player one-of link-neighbors
;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - payoff)
set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / max-payoff-difference)) [ [strategy] of observed-player ] [ strategy ] ;; If your strategy is the better, payoff-diff is negative, ;; so you are going to stick with it. ;; If it's not, you switch with probability ;; (payoff-diff / max-payoff-difference) end
Recall that the value of max-payoff-difference has to be set so the quotient (payoff-diff / max-payoff-difference) does not exceed 1, i.e. max-payoff-difference ≥ payoff-diff. The problem is that the maximum value of payoff-diff now depends on how payoffs are computed.
Let max-payoff-difference-in-matrix be the maximum payoff difference in the payoff matrix. If agents play once (play-with = “one-random-nbr“) or their payoff is an average (play-with = “all-nbrs-AVG-payoff“), then payoff-diff ≤ max-payoff-difference-in-matrix. However, if agents use the total payoff (play-with = “all-nbrs-TOTAL-payoff“), then the maximum value of payoff-diff can well be greater than max-payoff-difference-in-matrix. In that case, the maximum value of payoff-diff could be up to max-payoff-difference-in-matrix * max-n-of-nbrs-of-each-player, where max-n-of-nbrs-of-each-player is the maximum degree in the network.
Given all this, we should define global variables max-payoff-difference-in-matrix, max-payoff-difference and max-n-of-nbrs-of-each-player, and set their values accordingly.
globals [ payoff-matrix n-of-strategies n-of-players avg-nbrs-within-radius avg-clustering-coefficient size-of-largest-component max-payoff-difference-in-matrix ;; <== new line max-payoff-difference ;; <== new line max-n-of-nbrs-of-each-player ;; <== new line ]
Now we should set the value of these new global variables. Let us start with the easiest one: max-n-of-nbrs-of-each-player. This value is already computed at procedure to plot-accessibility. The only change we have to make is to replace let with set, since this variable is now global (because we want to read it from anywhere in the code).
to plot-accessibility let steps link-radius if link-radius = "Infinity" [set steps (n-of-players - 1)] let n-of-nbrs-of-each-player [(count nw:turtles-in-radius steps) - 1] of players ;; modified line below (let -> set) set max-n-of-nbrs-of-each-player max n-of-nbrs-of-each-player set-current-plot "Neighbors within link-radius" set-plot-x-range 0 (max-n-of-nbrs-of-each-player + 1) ;; + 1 to make room for the width of the last bar histogram n-of-nbrs-of-each-player set avg-nbrs-within-radius mean n-of-nbrs-of-each-player end
The best place to set the value of max-payoff-difference-in-matrix, is at procedure to update-payoff.
to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix
;; new lines below set max-payoff-difference-in-matrix (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) end
Note that we have to include the definition of two new procedures to compute the minimum and the maximum value of a matrix:
;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; SUPPORTING PROCEDURES ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;; ;;; Matrices ;;; ;;;;;;;;;;;;;;;;
to-report max-of-matrix [matrix] report max reduce sentence matrix end
to-report min-of-matrix [matrix] report min reduce sentence matrix end
Finally, let us set the value of max-payoff-difference in a new procedure created for that purpose.
to update-max-payoff-difference set max-payoff-difference max-payoff-difference-in-matrix * ifelse-value play-with = "all-nbrs-TOTAL-payoff" [max-n-of-nbrs-of-each-player][1] end
Once this procedure has been implemented, we can call it from to go to make sure that the value of max-payoff-difference is updated if the user changes the way payoffs are computed at runtime.
to go update-max-payoff-difference ;; <== new line ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph update-players-color end
To implement procedure to imitative-positive-proportional-m-rule, we can use the code we wrote for games played on grids, but before we should include the extension rnd at the beginning of our code
extensions [nw rnd]
Implementation of procedure to imitative-positive-proportional-m-rule
to imitative-positive-proportional-m-rule let chosen-nbr rnd:weighted-one-of my-nbrs-and-me [ payoff ^ m ] set strategy-after-revision [strategy] of chosen-nbr end
To avoid errors when payoffs are negative, we will include procedure to check-payoffs-are-non-negative, just like we did in the model for games played on grids.
to check-payoffs-are-non-negative if min reduce sentence payoff-matrix < 0 [ user-message (word "Since you are using decision-rule =\n" "imitative-positive-proportional-m,\n" "all elements in the payoff matrix\n" payoffs "\nshould be non-negative numbers.") ] end
An appropriate place to call this procedure would be at the end of procedure to setup-payoffs, which would then be as follows:
to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix
;; new lines below set max-payoff-difference (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) if decision-rule = "imitative-positive-proportional-m" [ check-payoffs-are-non-negative ] end
Feel free to implement procedure to Fermi-m-rule by yourself, looking at our previous implementation.
Implementation of procedure to Fermi-m-rule
A possible implementation of this procedure is as follows:
to Fermi-m-rule let observed-player one-of link-neighbors ;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - payoff) set strategy-after-revision ifelse-value (random-float 1 < (1 / (1 + exp (- m * payoff-diff)))) [ [strategy] of observed-player ] [ strategy ] end
Finally, looking at the description of “Santos-Pacheco” rule, please try to implement procedure to Santos-Pacheco-rule.
Implementation of procedure to Santos-Pacheco-rule
A possible implementation of this procedure is as follows:
to Santos-Pacheco-rule let observed-player one-of link-neighbors ;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - (payoff)) let degree count link-neighbors let degree-of-observed-player [count link-neighbors] of observed-player set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / (max-payoff-difference-in-matrix * max (list degree degree-of-observed-player)))) [ [strategy] of observed-player ] [ strategy ] end
With this, we have finished the implementation of the second extension to the model.
5.4. Complete code in the Code tab
We have finished our model!
extensions [nw rnd] globals [ payoff-matrix n-of-strategies n-of-players avg-nbrs-within-radius avg-clustering-coefficient size-of-largest-component max-payoff-difference-in-matrix ;; <== new line max-payoff-difference ;; <== new line max-n-of-nbrs-of-each-player ;; <== new line ] breed [players player] players-own [ strategy strategy-after-revision payoff my-nbrs-and-me ;; <== new line ] ;;;;;;;;;;;;; ;;; SETUP ;;; ;;;;;;;;;;;;; to setup clear-all setup-payoffs setup-players setup-graph reset-ticks update-graph compute-network-metrics end to setup-payoffs set payoff-matrix read-from-string payoffs set n-of-strategies length payoff-matrix ;; new lines below set max-payoff-difference-in-matrix (max-of-matrix payoff-matrix) - (min-of-matrix payoff-matrix) if decision-rule = "imitative-positive-proportional-m" [ check-payoffs-are-non-negative ] end to setup-players let initial-distribution read-from-string n-of-players-for-each-strategy if length initial-distribution != length payoff-matrix [ user-message (word "The number of items in\n" "n-of-players-for-each-strategy (i.e. " length initial-distribution "):\n" n-of-players-for-each-strategy "\nshould be equal to the number of rows\n" "in the payoff matrix (i.e. " length payoff-matrix "):\n" payoffs ) ] set n-of-players sum initial-distribution ifelse n-of-players < 4 [ user-message "There should be at least 4 players" ] [ build-network ask players [set strategy -1] let i 0 foreach initial-distribution [ j -> ask up-to-n-of j players with [strategy = -1] [ set payoff 0 set strategy i set strategy-after-revision strategy set my-nbrs-and-me ;; <== new line (turtle-set link-neighbors self) ;; <== new line ] set i (i + 1) ] set n-of-players count players update-players-color ] end ;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; NETWORK CONSTRUCTION ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;; to build-network set-default-shape players "circle" run (word "build-" network-model "-network") ask players [fd 15] end to build-Erdos-Renyi-network nw:generate-random players links n-of-players prob-link end to build-Watts-Strogatz-small-world-network nw:generate-watts-strogatz players links n-of-players (avg-degree-small-world / 2) prob-rewiring end to build-preferential-attachment-network nw:generate-preferential-attachment players links n-of-players min-degree end to build-ring-network nw:generate-ring players links n-of-players end to build-star-network nw:generate-star players links n-of-players end to build-grid-4-nbrs-network let players-per-line (floor sqrt n-of-players) nw:generate-lattice-2d players links players-per-line players-per-line false end to build-wheel-network nw:generate-wheel players links n-of-players end to build-path-network build-ring-network ask one-of links [die] end ;;;;;;;;;; ;;; GO ;;; ;;;;;;;;;; to go update-max-payoff-difference ;; <== new line ask players [update-payoff] ask players [ if (random-float 1 < prob-revision) [ update-strategy-after-revision ] ] ask players [update-strategy] tick update-graph update-players-color end ;;;;;;;;;;;;;;;;;;;;;;;;; ;;; UPDATE PROCEDURES ;;; ;;;;;;;;;;;;;;;;;;;;;;;;; to update-payoff if any? link-neighbors [ run (word "play-with-" play-with) ] end to play-with-one-random-nbr let mate one-of link-neighbors set payoff item ([strategy] of mate) (item strategy payoff-matrix) end to play-with-all-nbrs-TOTAL-payoff let n-of-coplayers-with-strategy-? n-values n-of-strategies [ i -> count link-neighbors with [strategy = i] ] let my-payoffs (item strategy payoff-matrix) set payoff sum (map * my-payoffs n-of-coplayers-with-strategy-?) end to play-with-all-nbrs-AVG-payoff play-with-all-nbrs-TOTAL-payoff set payoff (payoff / count link-neighbors) end to update-max-payoff-difference set max-payoff-difference max-payoff-difference-in-matrix * ifelse-value play-with = "all-nbrs-TOTAL-payoff" [max-n-of-nbrs-of-each-player][1] end to update-strategy-after-revision ifelse random-float 1 < noise [ set strategy-after-revision (random n-of-strategies) ] [ if any? link-neighbors [run (word decision-rule "-rule")] ] end to best-neighbor-rule set strategy-after-revision [strategy] of one-of my-nbrs-and-me with-max [payoff] end to imitate-if-better-rule let observed-player one-of link-neighbors if ([payoff] of observed-player) > payoff [ set strategy-after-revision ([strategy] of observed-player) ] end to imitative-pairwise-difference-rule let observed-player one-of link-neighbors
;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - payoff)
set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / max-payoff-difference)) [ [strategy] of observed-player ] [ strategy ] ;; If your strategy is the better, payoff-diff is negative, ;; so you are going to stick with it. ;; If it's not, you switch with probability ;; (payoff-diff / max-payoff-difference) end to imitative-positive-proportional-m-rule let chosen-nbr rnd:weighted-one-of my-nbrs-and-me [ payoff ^ m ] set strategy-after-revision [strategy] of chosen-nbr end to Fermi-m-rule let observed-player one-of link-neighbors ;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - payoff) set strategy-after-revision ifelse-value (random-float 1 < (1 / (1 + exp (- m * payoff-diff)))) [ [strategy] of observed-player ] [ strategy ] end to Santos-Pacheco-rule let observed-player one-of link-neighbors ;; compute difference in payoffs let payoff-diff ([payoff] of observed-player - (payoff)) let degree count link-neighbors let degree-of-observed-player [count link-neighbors] of observed-player set strategy-after-revision ifelse-value (random-float 1 < (payoff-diff / (max-payoff-difference-in-matrix * max (list degree degree-of-observed-player)))) [ [strategy] of observed-player ] [ strategy ] end to update-strategy set strategy strategy-after-revision end ;;;;;;;;;;;;; ;;; PLOTS ;;; ;;;;;;;;;;;;; to setup-graph set-current-plot "Strategy Distribution" foreach (range n-of-strategies) [ i -> create-temporary-plot-pen (word i) set-plot-pen-mode 1 set-plot-pen-color 25 + 40 * i ] end to update-graph let strategy-numbers (range n-of-strategies) let strategy-frequencies map [ n -> count players with [strategy = n] / n-of-players ] strategy-numbers set-current-plot "Strategy Distribution" let bar 1 foreach strategy-numbers [ n -> set-current-plot-pen (word n) plotxy ticks bar set bar (bar - (item n strategy-frequencies)) ] set-plot-y-range 0 1 end to update-players-color ask players [set color 25 + 40 * strategy] end ;;;;;;;;;;;;;;;;;;;;;;; ;;; NETWORK METRICS ;;; ;;;;;;;;;;;;;;;;;;;;;;; to compute-network-metrics plot-accessibility compute-avg-clustering-coefficient compute-size-of-largest-component end to plot-accessibility let steps link-radius if link-radius = "Infinity" [set steps (n-of-players - 1)] let n-of-nbrs-of-each-player [(count nw:turtles-in-radius steps) - 1] of players ;; modified line below (let -> set) set max-n-of-nbrs-of-each-player max n-of-nbrs-of-each-player set-current-plot "Neighbors within link-radius" set-plot-x-range 0 (max-n-of-nbrs-of-each-player + 1) ;; + 1 to make room for the width of the last bar histogram n-of-nbrs-of-each-player set avg-nbrs-within-radius mean n-of-nbrs-of-each-player end to compute-avg-clustering-coefficient set avg-clustering-coefficient mean [ nw:clustering-coefficient ] of players end to compute-size-of-largest-component set size-of-largest-component max map count nw:weak-component-clusters end ;;;;;;;;;;;;;; ;;; LAYOUT ;;; ;;;;;;;;;;;;;; ;; Procedures taken from Wilensky's (2005a) NetLogo Preferential ;; Attachment model ;; http://ccl.northwestern.edu/netlogo/models/PreferentialAttachment ;; and Wilensky's (2005b) Mouse Drag One Example ;; http://ccl.northwestern.edu/netlogo/models/MouseDragOneExample to relax-network ;; the number 3 here is arbitrary; more repetitions slows down the ;; model, but too few gives poor layouts repeat 3 [ ;; the more players we have to fit into ;; the same amount of space, the smaller ;; the inputs to layout-spring we'll need to use let factor sqrt count players ;; numbers here are arbitrarily chosen for pleasing appearance layout-spring players links (1 / factor) (7 / factor) (3 / factor) display ;; for smooth animation ] ;; don't bump the edges of the world let x-offset max [xcor] of players + min [xcor] of players let y-offset max [ycor] of players + min [ycor] of players ;; big jumps look funny, so only adjust a little each time set x-offset limit-magnitude x-offset 0.1 set y-offset limit-magnitude y-offset 0.1 ask players [ setxy (xcor - x-offset / 2) (ycor - y-offset / 2) ] end to-report limit-magnitude [number limit] if number > limit [ report limit ] if number < (- limit) [ report (- limit) ] report number end to drag-and-drop if mouse-down? [ let candidate min-one-of players [distancexy mouse-xcor mouse-ycor] if [distancexy mouse-xcor mouse-ycor] of candidate < 1 [ ;; The WATCH primitive puts a "halo" around the watched turtle. watch candidate while [mouse-down?] [ ;; If we don't force the view to update, the user won't ;; be able to see the turtle moving around. display ;; The SUBJECT primitive reports the turtle being watched. ask subject [ setxy mouse-xcor mouse-ycor ] ] ;; Undoes the effects of WATCH. reset-perspective ] ] end ;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; SUPPORTING PROCEDURES ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;; to check-payoffs-are-non-negative if min reduce sentence payoff-matrix < 0 [ user-message (word "Since you are using decision-rule =\n" "imitative-positive-proportional-m,\n" "all elements in the payoff matrix\n" payoffs "\nshould be non-negative numbers.") ] end ;;;;;;;;;;;;;;;; ;;; Matrices ;;; ;;;;;;;;;;;;;;;;
to-report max-of-matrix [matrix] report max reduce sentence matrix end to-report min-of-matrix [matrix] report min reduce sentence matrix end
6. Sample runs
6.1. Cooperation on preferential-attachment networks
Now that we have our model ready, we can replicate some of the results put forward by Santos and Pacheco (2005, 2006) and Santos et al. (2006a, 2006b).[2] These authors observed that scale-free networks (especially preferential-attachment networks created following the Barabási–Albert model) can promote cooperation in social dilemmas. Let us see this with our new model.
Figure 6 below shows a representative simulation run of a population of 10 000 agents who play the Prisoner’s Dilemma with payoffs [[0 1.1875] [-0.1875 1]], using total payoffs and Santos-Pacheco decision rule. Strategy 0 (orange) corresponds to defection and strategy 1 (green) corresponds to cooperation. The network is preferential attachment with min-degree 2 (average degree ≈ 4). As you can see, the whole population reaches very high levels of cooperation (green) after a few thousand ticks. This is our baseline setting.

The whole simulation setting for figure 6 (i.e., baseline setting) is included below, in case you want to run it for yourself. We chose 10 000 agents to match the original experiments, but feel free to use a smaller population (e.g. 1000 agents) so the model runs faster. Results will be very similar.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
The cooperation obtained for the preferential attachment network in our baseline setting vanishes if the model is run on more homogeneous networks where all agents have a similar number of link-neighbors. To see this, let us run a few simulations on Watts-Strogatz networks. In contrast with preferential attachment networks, Watts-Strogatz networks have degree distributions that tend to be clustered around the mean. As you can see in Table 1 below, defection prevails on these networks.
| Rewiring probability | Representative simulation | Degree Distribution |
|---|---|---|
| 0 | 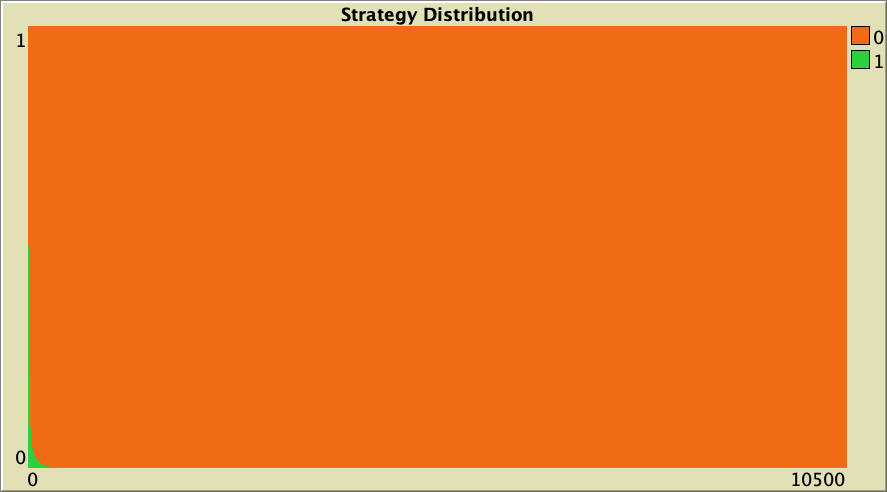 |
 |
| 0.25 | 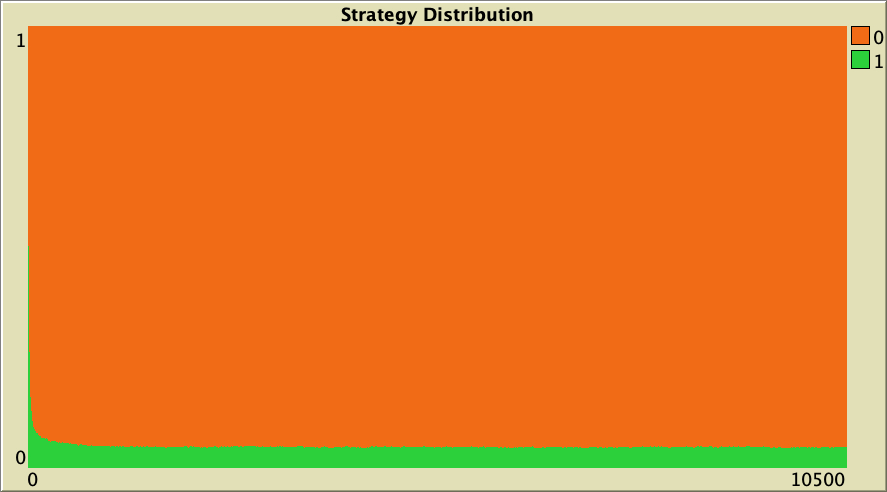 |
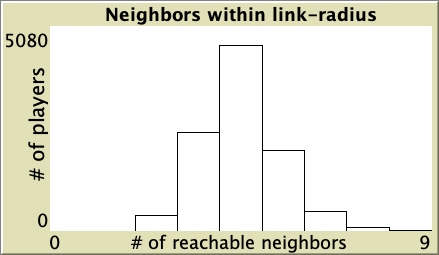 |
| 0.50 | 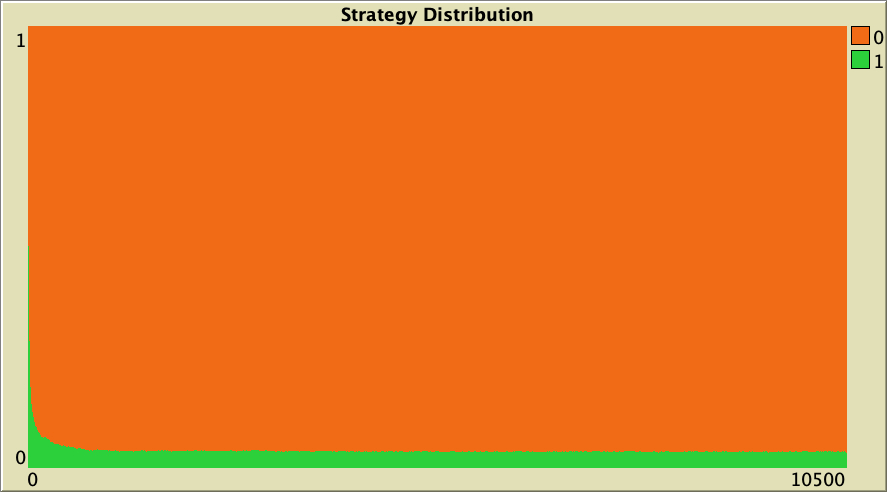 |
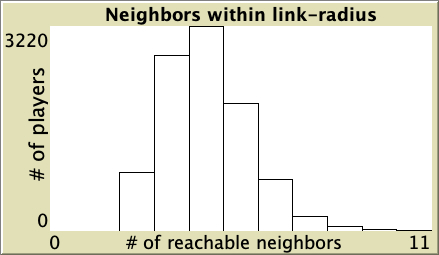 |
| 0.75 | 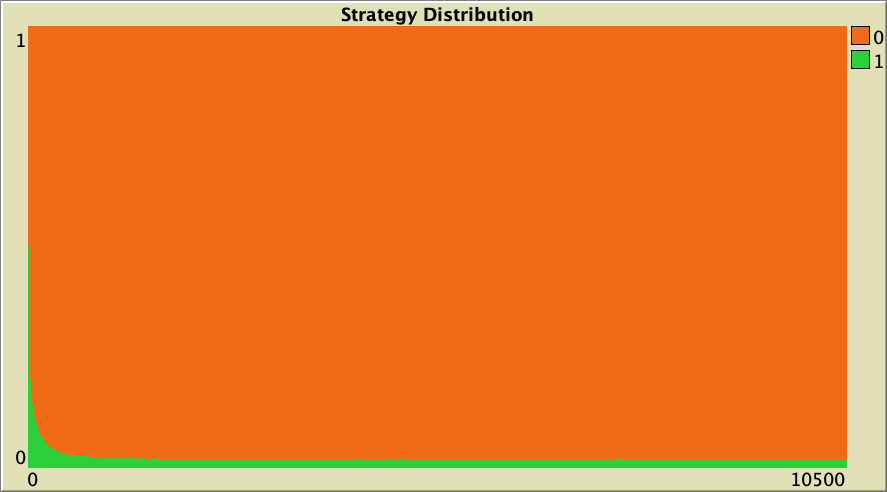 |
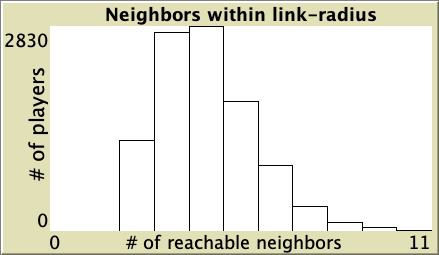 |
| 1 | 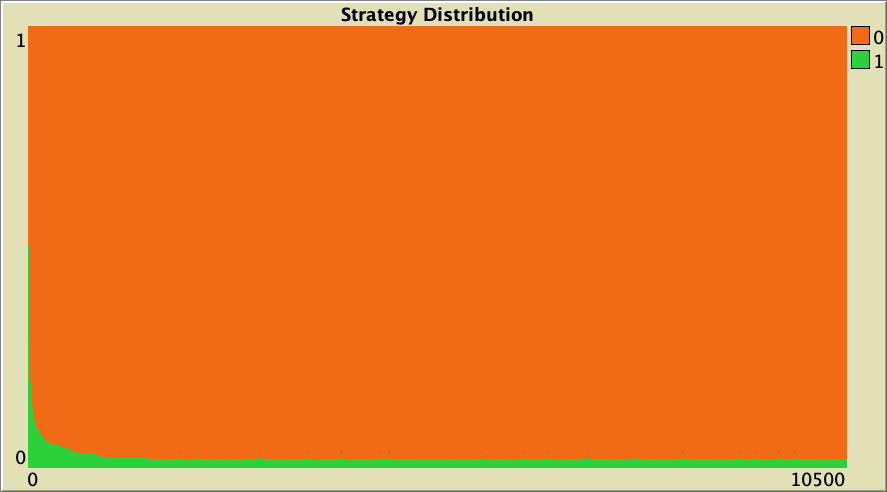 |
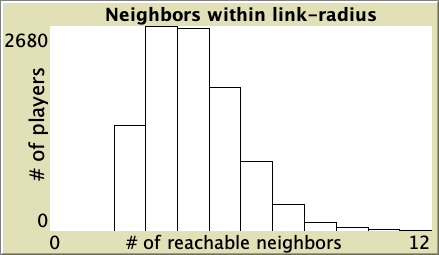 |
Table 1. Representative simulations of a population of 10 000 agents who play the Prisoner’s Dilemma with payoffs [[0 1.1875] [-0.1875 1]], using total payoffs and Santos-Pacheco decision rule. The networks are Watts-Strogatz with average degree 4 and different rewiring probabilities
The parameter values used for the simulations shown in Table 1 are included below.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "Watts-Strogatz-small-world"] ["avg-degree-small-world" 4] ["prob-rewiring" [0 0.25 0.5 0.75 1]] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
How does cooperation emerge in Barabási–Albert scale-free networks? The mechanism, which is explained by Santos and Pacheco (2006), Szabó and Fáth (2007, section 6.8), and Gómez-Gardeñes et al. (2007), relies on using total (accumulated) payoffs.
Finally, we would like to point out that the results for the evolution of cooperation are affected if, instead of using the accumulated payoff for each agent, its fitness is associated with the accumulated payoff divided by the number of interactions each agent engages during his life-cycle. Santos and Pacheco (2006, p. 732)
If agents use average (rather than total) payoffs, cooperation is severely undermined (see e.g. Wu et al. (2005), Wu et al. (2007), Tomassini et al. (2007), Szolnoki et al. (2008), Antonioni and Tomassini (2012), and Maciejewski et al. (2014)).[3] In the next section, we run some simulations to illustrate this.
6.2. Robustness of cooperation on scale-free preferential-attachment networks
In this final section, we run a few simulations to check the robustness of the emergence of cooperation on preferential-attachment networks.
The crucial importance of using total (accumulated) payoffs
First, we corroborate that, indeed, if agents use average payoffs rather than total payoffs, cooperation levels drop. In our model, this is best checked by using the imitative pairwise-difference decision rule. When using average payoffs, the only difference between the imitative pairwise-difference decision rule and Santos-Pacheco rule is that the latter divides the normalized payoff difference by ![]() , and this seems unnecessary since the normalized payoff difference is already in the range [0,1]. In any case, the results using Santos-Pacheco rule are qualitatively the same, so feel free to use that rule to run the experiments below, if you like.
, and this seems unnecessary since the normalized payoff difference is already in the range [0,1]. In any case, the results using Santos-Pacheco rule are qualitatively the same, so feel free to use that rule to run the experiments below, if you like.
Figure 7 below shows a representative simulation run with the same baseline setting as in figure 6, but using average rather than total payoffs. As you can see, the level of cooperation quickly drops to very low values.
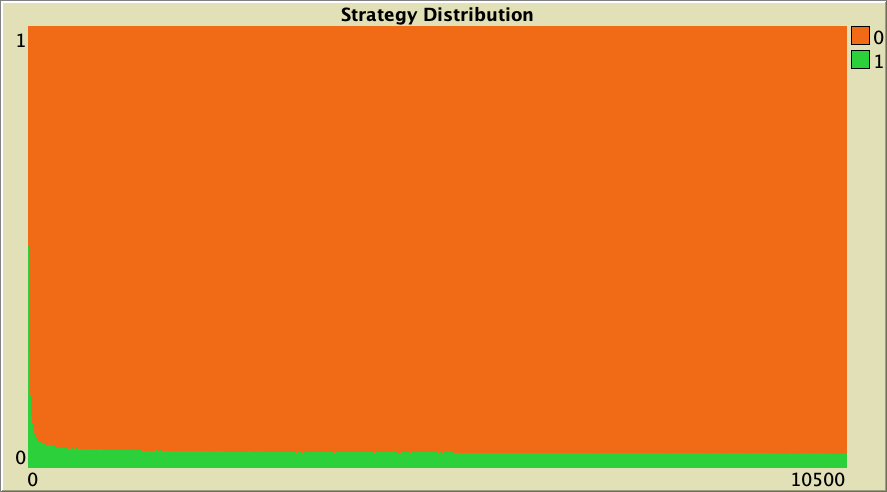
The whole simulation setting for figure 7 is included below, in case you want to run it for yourself.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "imitative-pairwise-difference"] ["play-with" "all-nbrs-AVG-payoff"] ["prob-revision" 1] ["noise" 0]
The results for the case where agents play with one random neighbor are even clearer (see figure 8). The whole population defects after only a few ticks.
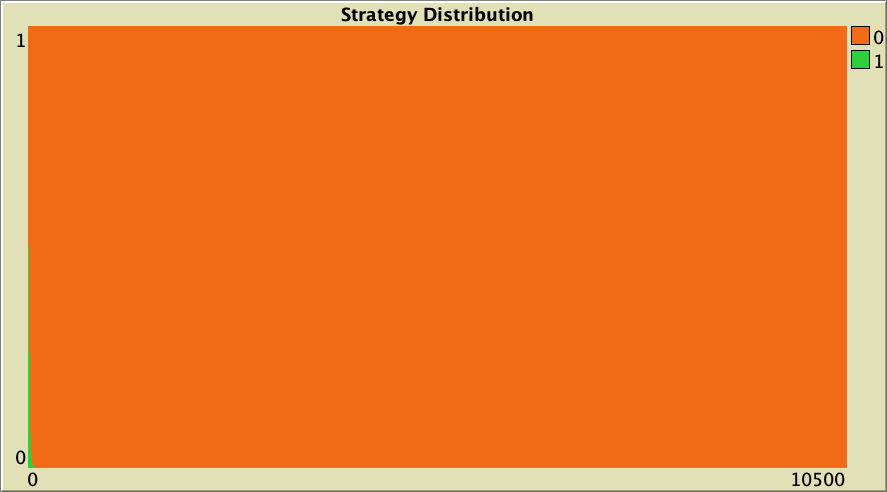
The whole simulation setting for figure 8 is included below, in case you want to run it for yourself.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "imitative-pairwise-difference"] ["play-with" "one-random-nbr"] ["prob-revision" 1] ["noise" 0]
Random noise
It turns out that the emergence of cooperation in preferential-attachment networks is also quite sensitive to random noise. Figure 9 below shows a representative simulation with the same baseline setting as in figure 6, but adding a little bit of noise (noise = 0.01). Adding this little noise decreases the level of cooperation from nearly 100% to about 50%.
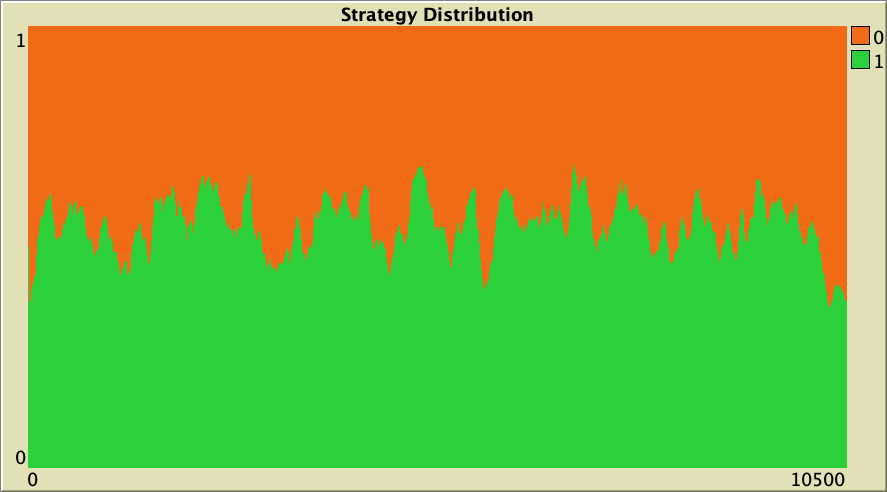
The whole simulation setting for figure 9 is included below, in case you want to run it for yourself.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0.01]
Payoff values
As we saw in Part III, local interactions in structured populations (as opposed to global interactions in well-mixed populations) can often promote cooperation, but only to some extent, i.e. within a limited range of payoff values. In general, one can make cooperation vanish by modifying the payoffs in a way that favors defectors.
As an example, figure 10 below shows a representative simulation run with the same baseline setting as in figure 6, but replacing Temptation = 1.1875 with Temptation = 1.375 and Suckers = -0.1875 with Suckers = -0.375. This small change in payoff values consistently leads to full defection in a few hundred ticks.
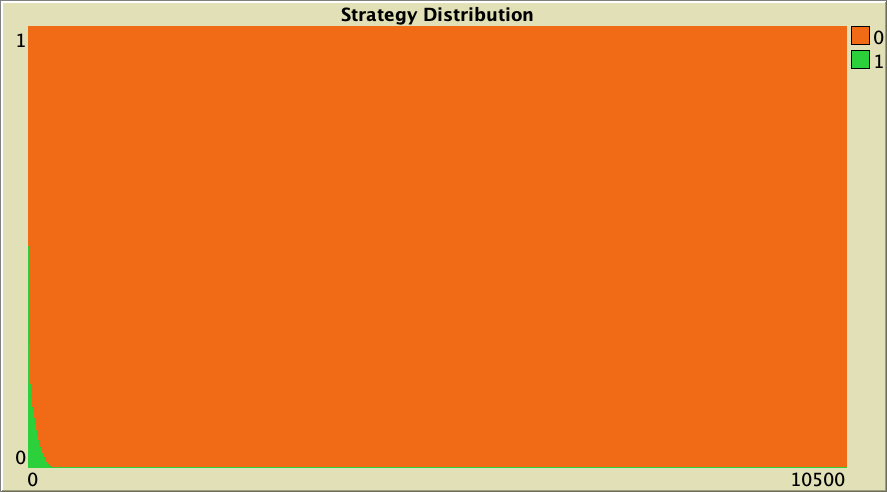
The whole simulation setting for figure 10 is included below.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[0 1.375]\n [-0.375 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
Payoff translations or interaction costs
When all agents play the game the same number of times or when they use average payoffs, many decision rules are invariant to positive affine transformations of payoffs. In other words, one can multiply all payoffs by a positive constant and/or add any constant to all payoffs, and the dynamics will not be affected.
However, in networks where agents use total payoffs and they have different numbers of neighbors, this is often no longer the case. Decision rule Santos-Pacheco in preferential-attachment networks is a case in point (Tomassini et al., 2007).
As an example, figure 11 below shows a representative simulation run with the same baseline setting as in figure 6, but where we have subtracted 0.25 from all payoffs. This 0.25 can be interpreted as a cost for every interaction where agents are involved (Masuda, 2007). As you can see, this small subtraction to all payoff values significantly decreases the level of cooperation.
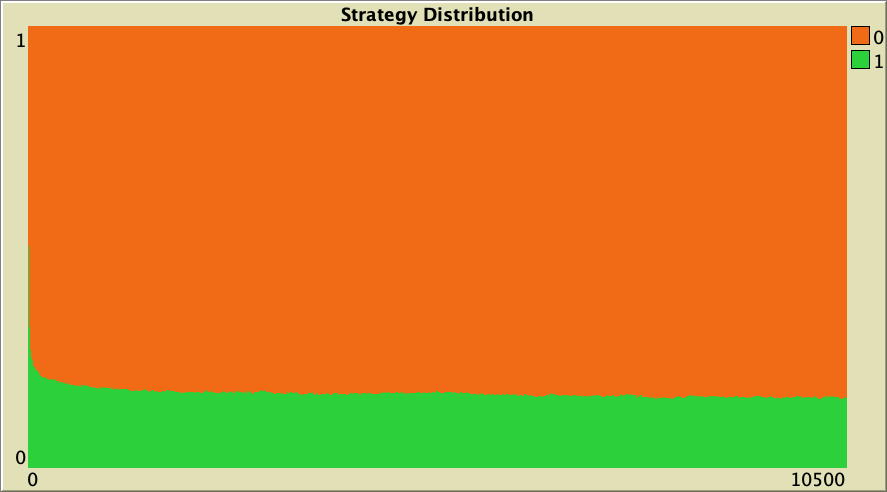
The whole simulation setting for figure 11 is included below.
["n-of-players-for-each-strategy" "[5000 5000]"] ["payoffs" "[[-0.25 0.9375]\n [-0.4375 0.75]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
Initial conditions
Note that the state where everyone defects is absorbing. Also, we can think of nearby states such that if we start a simulation there, the system will evolve to the state of full defection. States with one single cooperator are clear examples. This suggests that, in general, the state of full defection will have some basin of attraction. In other words, if we choose initial conditions close enough to the state of full defection, it is likely that the simulation will end up with the whole population defecting.
In our baseline setting, it turns out that the basin of attraction of the state of full defection is quite sizable. As an example, Figure 12 below shows a representative simulation with the same baseline setting as in figure 6, but with initial conditions [9000 1000]. Most simulation runs with these initial conditions end up with no cooperation at all.
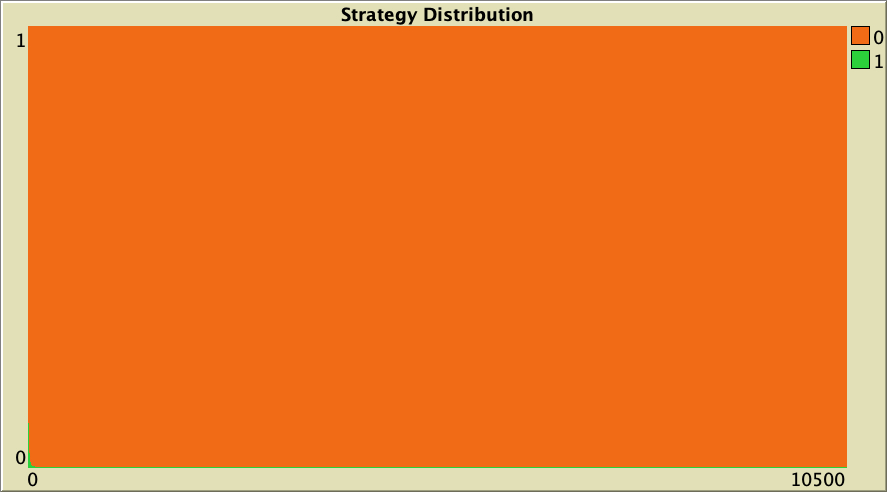
The whole simulation setting for figure 12 is included below, in case you want to run it for yourself.
["n-of-players-for-each-strategy" "[9000 1000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
We also get very low cooperation levels if we start from initial conditions a bit further away from the state of full defection. As an example, Figure 13 below shows a representative simulation with the same baseline setting as in figure 6, but with initial conditions [8000 2000].
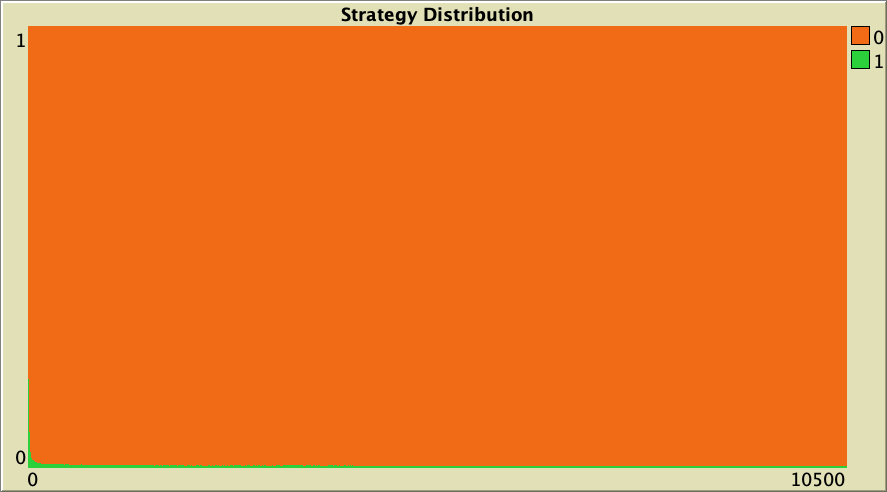
The whole simulation setting for figure 13 is included below, in case you want to run it for yourself.
["n-of-players-for-each-strategy" "[8000 2000]"] ["payoffs" "[[0 1.1875]\n [-0.1875 1]]"] ["network-model" "preferential-attachment"] ["min-degree" 2] ["decision-rule" "Santos-Pacheco"] ["play-with" "all-nbrs-TOTAL-payoff"] ["prob-revision" 1] ["noise" 0]
Final thoughts
We are approaching the end of our journey together, and by now we hope that the following words we wrote in the preface of this book start to make some sense to you:
To use a scientific model rigorously, it is important to be fully aware of all the assumptions embedded in it, and also of the various alternative assumptions that could have been chosen. If we don’t understand all the details of a model, we run the risk of over-extrapolating its scope and of drawing unsound conclusions.
In this chapter we have seen –once again– that the dynamics of evolutionary models can often be significantly affected by a multitude of factors that may not seem very relevant at first sight. This implies that in most cases it is extremely hard, if not impossible, to derive general simple rules about evolutionary dynamics on networks. For good or for bad, this is the way our universe seems to work, and there is nothing we can do to change that.
On a more positive note, this reflection highlights –once again– the importance of the skills you have learned. You are now able to design, implement and analyze models that can help you derive sound conclusions. The scope of these conclusions will often be more limited than what we would have wished for, but there is not much we can do about that. What is definitely under our control is to make sure that our conclusions are sound and rigorous, and by following this book you have taken a huge step in that direction.
7. Exercises
You can use the following link to download the complete NetLogo model: nxn-games-on-networks.nlogo.
Exercise 1. How can we parameterize our model to replicate the results shown in figure 2 of Santos and Pacheco (2005)?
Exercise 2. How can we parameterize our model to replicate the results shown in figure 6 of Santos and Pacheco (2006)?
Exercise 3. How can we parameterize our model to replicate the results shown in figure 5 of Tomassini et al. (2007)?
![]() Exercise 4. In our model, all revising agents update their strategy synchronously. What changes would you have to make in the code so revising agents within the tick update their strategies sequentially (in random order), rather than simultaneously?
Exercise 4. In our model, all revising agents update their strategy synchronously. What changes would you have to make in the code so revising agents within the tick update their strategies sequentially (in random order), rather than simultaneously?
Hint to implement asynchronous strategy updating
It is possible to do this by making a couple of minor changes in procedure to go, without touching the rest of the code.
Exercise 5. How can we parameterize the model developed in exercise 4 above to replicate the results shown in figure 2 of Tomassini et al. (2007)?
Exercise 6. For our “sample runs”, we have used unconventional payoff values, such as 1.1875, -0.1875, 1.375 or -0.375. Can you guess why did we not use better looking numbers such as 1.2, -0.2, 1.4 and -0.4 instead?
Hint
Write all these decimal numbers in binary. If you use a finite number of bits, once you have converted all these decimal numbers to finite bit strings, convert the binary representations back into decimal base.
- This variant has been used in several papers, such as Santos and Pacheco (2006), Santos et al. (2006a, 2006b), Gómez-Gardeñes et al. (2007) and Poncela et al. (2007). ↵
- The algorithm these authors use to generate scale-free networks is slightly different from the one implemented in NetLogo. They start with an empty network, while we start with a complete network. This is a very small difference that is immaterial for our purposes. ↵
- Tomassini et al. (2007), Szolnoki et al. (2008) and Antonioni and Tomassini (2012) develop models to study the transition from the extreme setting of total payoffs to the opposite extreme setting of average payoffs in a continuous way. ↵

