5 Carbocation Relative Energy and Alkene Addition Reaction Regioselectivity
In the previous example, the alkene substrate is a symmetric alkene. In contrast, an unsymmetrical alkene has the two groups bonded to one of the doubly-bonded carbon differ from those on the other carbon. For example, in propene, one of the sp2 carbon has two H bonded to it, while the other sp2 carbon has an H and a methyl group bonded to it.
When propene undergo addition reaction with HBr, two constitutional isomeric products are possible depending on which carbon in the double bond bonds to the H and which to the Br.

The two products are formed from two separate reaction pathways starting from the same reactants—these two pathways are in competition (competing for the same starting material). Experimentally, 2-bromopropane is observed to be the major product, while 1-bromopropane is the minor product (in fact, negligible amount of it is formed under typically reaction conditions). In other words, this reaction is regioselective, where one of the possible constitutional isomer products are formed in excess over the other(s).
Under typical conditions, the HX addition to alkene reaction is kinetically controlled, where the product selectivity is dictated by the relative rates of the competing reaction pathways. This is because the addition of Br– to the carbocation is not reversible under typical conditions, preventing the reaction from reaching equilibrium.
Therefore, the rate of 2-bromopropane formation must be faster than the rate of 1-bromopropane formation in order for it to be the major product. For both reaction pathways, the rate of the overall reaction is the rate of the first step, the RDS:
Rate = k[propene][HBr]
Given that the starting material concentrations are the same in both cases, the difference here lies in the rate constant, k,
k = Ae−Ea/RT
where A is the pre-exponential factor, Ea is the activation energy, R is the gas constant (8.314 ![]() ), and T is the temperature. The competing reactions are occurring in the same reaction vessel, therefore they are under the same temperature. Similarly, starting from the same reactants, the pre-exponential factor would be the same. Hence, the dictating factor here is the difference in the activation energy, and the pathway with the lower Ea will have a faster rate, leading to the major product.
), and T is the temperature. The competing reactions are occurring in the same reaction vessel, therefore they are under the same temperature. Similarly, starting from the same reactants, the pre-exponential factor would be the same. Hence, the dictating factor here is the difference in the activation energy, and the pathway with the lower Ea will have a faster rate, leading to the major product.
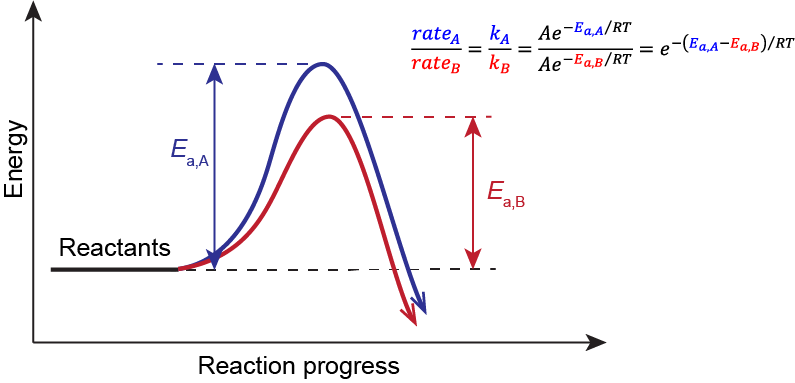
Hammond’s Postulate
Consider the two competing pathways outlined in Figure 1. They have different rates because they differ in their RDS (step 1). And because they start from the same reactants, if we know which transition state 1 structure is lower in energy, we will know which Ea is lower and therefore which pathway would be faster.
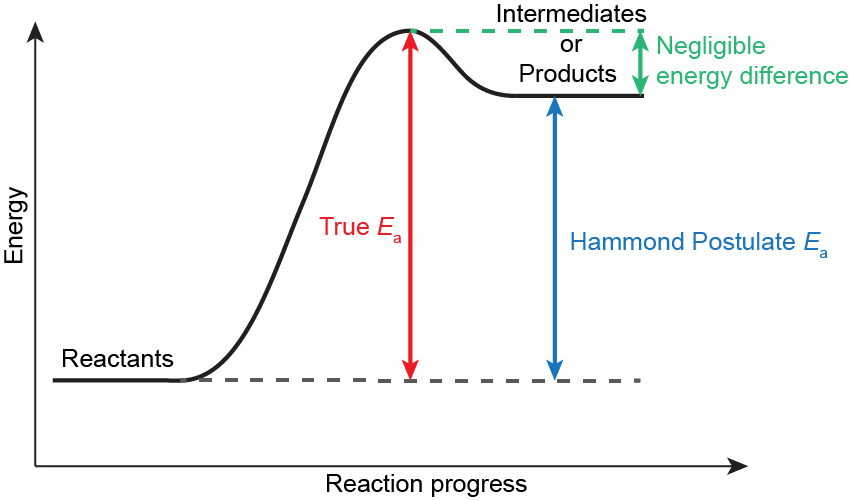
However, transition state complexes are highly unstable, existing on maxima on the reaction coordinate diagrams. They have fleeting existences and are extremely difficult to study directly. To gain insight into a particular transition state, we invoke Hammond’s postulate, which states that “If two states, as, for example, a transition state and an unstable intermediate, occur consecutively during a reaction process and have nearly the same energy content, their interconversion will involve only a small reorganization of the molecular structures.”
In other words, for the HX addition to alkene reaction, the structure and energy of the first transition state can be approximated by the structure and energy of the carbocation intermediate. Therefore, any structural features that can lower the energy of a carbocation intermediate will also lower the energy of the corresponding transition state, thereby speeding up the reaction. If we understand the relative energies of carbocations, we can predict the relative energies of the transition states and, by extension, which pathway is the faster one.
Exercise 1: Hammond’s Postulate
Explain Hammond’s Postulate using the potential energy surface shown below. Make sure to explain each of the energies labeled and what is required for Hammond’s Postulate to be valid.
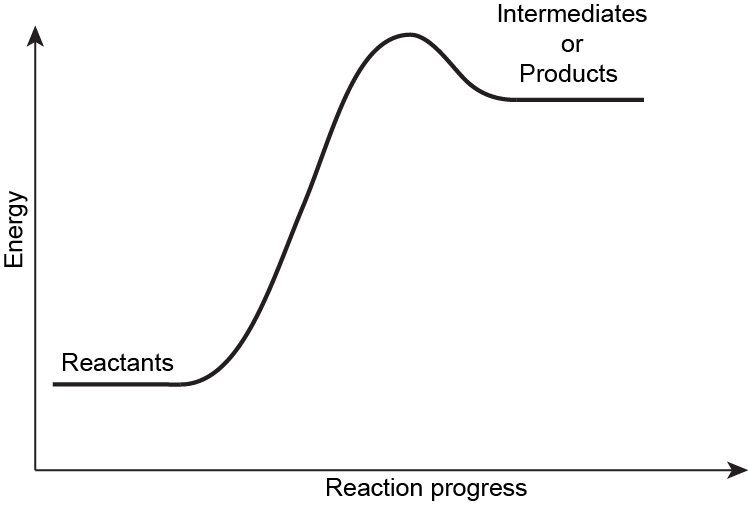
Write in your notebook, then left-click here for an explanation.
Hammond’s postulate allows the energy of a high-energy intermediate or product to be used as a proxy for the energy of a transition state. It is valid if the structures and energies of the intermediate (or product) and transition state are similar.
Relative Energy of Carbocations
The sp2 carbon atom in a carbocation is electron deficient—it is surrounded by only six valence electrons, which are involved in the three σ bonds to the three groups arranged in a trigonal planar geometry around that carbon. It has an unoccupied p orbital that is perpendicular to the plane created by the σ bonds.
Carbocations can be classified based on the number of alkyl groups attached to the sp2 carbon: a tertiary (3°) carbocation has three alkyl groups, a secondary (2°) carbocation has two alkyl groups, and a primary (1°) carbocation has one alkyl group. If no alkyl groups are attached, that is a methyl carbocation.

For an example of relative carbocation stability, consider the following ΔfH° values of three C4H9+ carbocation isomers.
| n-butyl cation | 803 kJ/mol | 1° carbocation | |
| sec-butyl cation | 769 kJ/mol | 2° carbocation | |
| tert-butyl cation | 711 kJ/mol | 3° carbocation |
These values show that more alkyl substituents on the sp2 carbon leads to lower energy carbocation, with a tertiary carbocation being lowest in energy. Similar to the alkene isomers, this trend is due to a combination of bond strengths and hyperconjugation.
The bond strength consideration is essentially the same as alkene isomers: a carbocation with more alkyl substituents has more σC(sp3)-C(sp2) bonds and less σC(sp3)-C(sp3) bonds, making it lower in energy compared to an isomer with less substituents.
However, unlike the difference in energy between alkene isomers, which are typically <10 kJ/mol per substituent, the relative energies of carbocation isomers differ by ~50 kJ/mol per substituent. This larger difference is accounted for by hyperconjugation, where the overlap of the filled C-H (or C-C in larger alkyl groups) σ bonding orbitals with the empty p orbital leads to delocalization of the electron densities. As a result, the two electrons that are nominally involved in the C-H σ bond have some of their densities delocalized to the electron-deficient sp2 carbon, thereby stabilizing the high energy complex.

Each off-plane C-H bond in an alkyl substituent can overlap with the empty p orbital, and as the number of alkyl substituents increases, the number of σ bonds available for hyperconjugation increases. Hence, the tert-butyl cation in the table above is the lowest energy isomer. If we look at the actual charges in the tert-butyl cation, the central carbon only has a charge of +0.469, while each methyl group has a charge of +0.178. In other words, electron delocalization via hyperconjugation spread out the +1 charge in the carbocation to the alkyl substituents.
[should the sigma bond resonance structure drawing be included here?]
Exercise 2: Relative energy of carbocations
Label the hybridization of each C-atom in the molecules below.
Which carbocation is the lowest in energy? justify your answer.
Write in your notebook, then left-click here for an explanation.
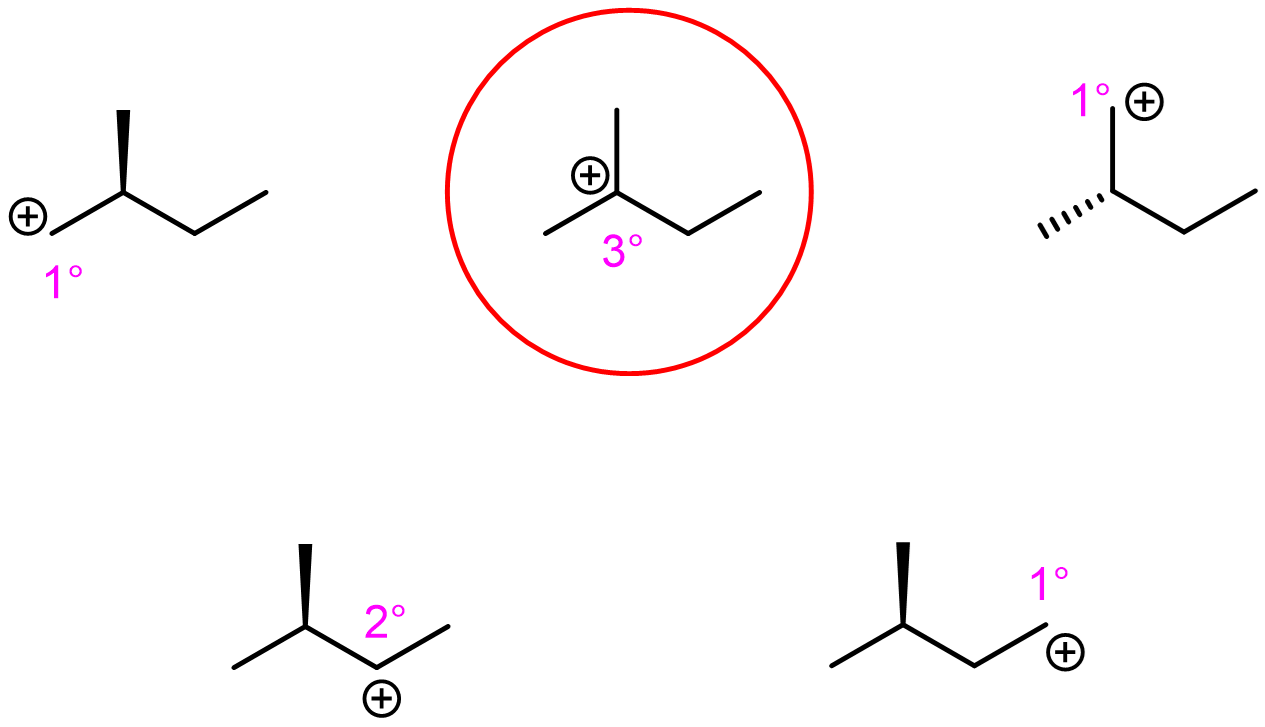
Among the choices, there is only one tertiary carbocation. It is the lowest energy.
Just as electron delocalization via hyperconjugation can lower the energy of a carbocation, electron delocalization via a π conjugation can also lower the carbocation’s energy. However, we must first consider whether the conjugated π system involves the nominally empty 2p orbital.
Exercise 3: Relative energy of carbocations
Identify the most stable carbocation and justify your answer.
Write in your notebook an explanation for your answer, then left-click here.

At a quick glance, it may appear that all the carbocations here are 1° carbocations. However, the allyl carbocation has π conjugation involving the nominally empty 2p orbital. This π conjugation delocalizes the positive charge and lowers the energy of the carbocation.

(Note that in the vinyl carbocations, the empty 2p orbital is on a sp carbon that is also involved in the π bond. The π bond is perpendicular to the p orbital, and neither is involved in any π conjugation.)
Regioselectivity
We can now understand why 2-bromopropane is observed to be the major product in the reaction between propene and HBr. In the two competing pathways depicted in Figure 1, the one leading to the formation of 2-bromopropane involves forming a lower energy 2° carbocation as opposed to a 1° carbocation. Therefore, 2-bromopropane forms much faster than 1-bromopropane, and it is the major product.
This regioselectivity of electrophilic addition of HX to alkenes follows Markovnikov’s rule, proposed by Russian chemist Vladimir Markovnikov in 1869: the H (from HX) attaches to the double-bonded carbon with the fewer alkyl substituents, and the X attaches to the double-bonded carbon with the more alkyl substituents.
Markovnikov’s rule allows us to predict the major product in electrophilic addition of HX to alkene reactions. But to understand why Markovnikov’s rule applies for this class of reactions, we must invoke Hammond’s postulate and understand the relative energies of carbocations.
Exercise 4: Reaction energy diagram
On the reaction energy diagram below, place all of the reactants, products, and intermediates of the reaction shown in Figure 1 in their appropriate locations. Additionally, draw the missing transition states for each step of the reaction. (After you have drawn in your notebook, click on each ? to see the answer.)
Use Hammond’s postulate and the reaction energy diagram to explain which product should be expected from this reaction.
Write in your notebook, then left-click here for an explanation.
Exercise 5:
Hydrochloric acid (HCl) is a very strong acid capable of performing an electrophilic addition to an alkene via a high-energy carbocation intermediate. The rate and regiochemistry of this reaction (Markovnikov’s rule) can be rationalized by the relative stability of the carbocation intermediate.

Explore this reaction between HCl and 1-methylcyclohexene. The stereoisomerism of the minor products and conformational isomers of cyclohexane derivatives will be discussed in more detail in later sections.
- The electrophilic addition of HCl begins by the protonation of an alkene πC–C bond. The formation of a carbocation (strong acid, high-energy intermediate) is generally unfavorable and requires a strong acid such as HCl. Draw an electron-pushing mechanism for the reaction of HCl and 1-methylcyclohexene. Label the hybridization before and after the reaction of each carbon participating in the reaction. Finally, draw the transition state leading to each carbocation regioisomer.
Draw the electron-pushing mechanism and transition states in your notebook, then left-click here.

- The protonation step of this reaction, part (a), involves a donor orbital on the base and an acceptor orbital on the acid. In order for the σC–H bond to form and the σH–Cl bond to break, the two molecules must approach each other in appropriate orientations that allow the donor and acceptor orbitals to overlap. Use the orbitals shown in the link for HCl and 1-methylcyclohexene to describe the orientation of the molecules necessary for a reaction to occur.
Draw in your notebook, then left-click here.
HCl must approach the π bond from above or below the ring with the chloride aimed away. For example,

- The two carbocation regioisomers are tertiary and secondary, with the 2° carbocation being 12.0 kcal/mol higher in energy. (click on the links to see the empty p orbital on these carbocations.) Explain the energy difference between these two carbocation intermediates, making specific reference to charge delocalization.
Write in your notebook, then left-click here.
The 3° carbocation has more adjacent σ bonds that can donate electron density via hyperconjugation to stabilize the positive charge. (The adjacent σ bonding orbitals must overlap the empty p orbital to hyperconjugate.)
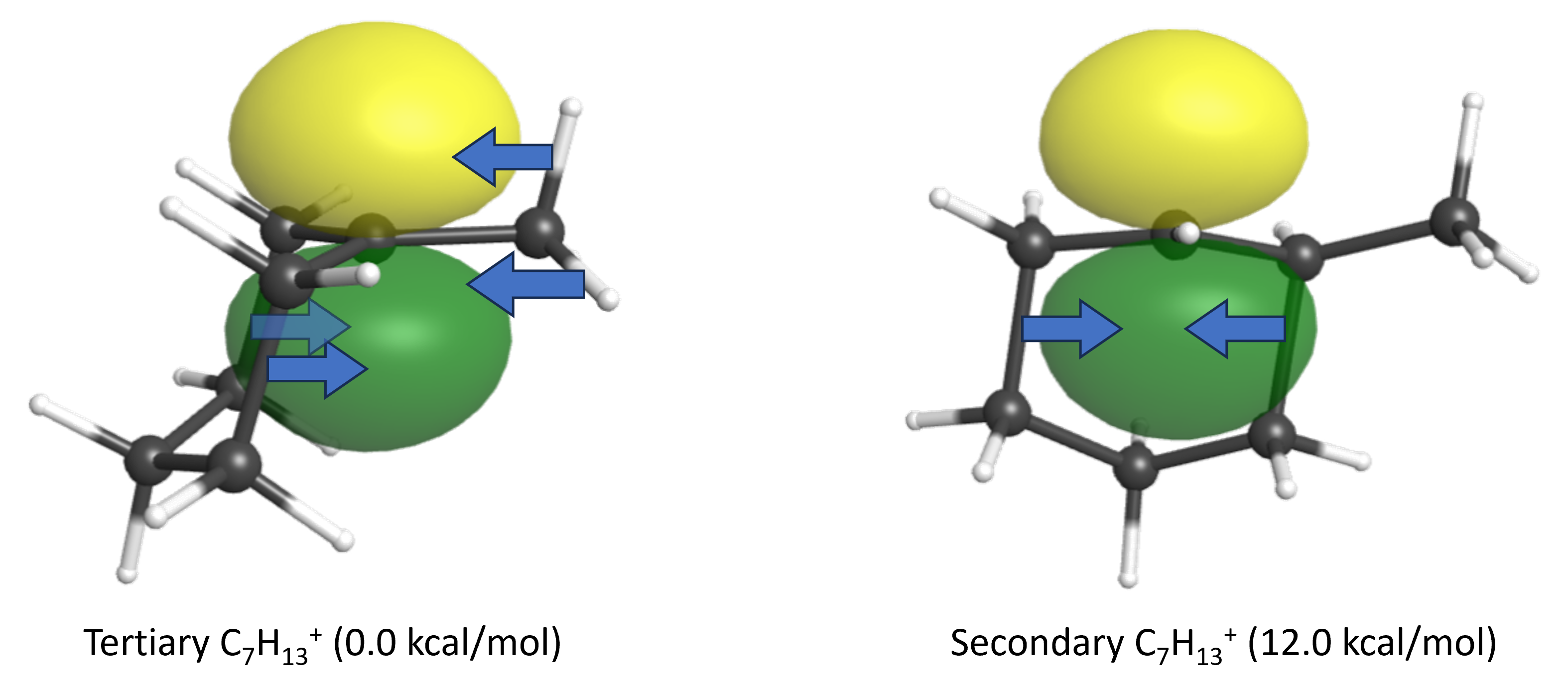
- The second step of the electrophilic addition involves σC–Cl bond formation by donor-acceptor interaction from a filled orbital on the nucleophile (Cl–) and the empty orbital on the electrophile. Complete the electron-pushing mechanism below.
Use the orbital from part (c) to depict and describe how the chloride ion can attach to the empty p orbital on the carbocation.
Write in your notebook, then left-click here.
The empty p orbital has two same-sized lobe above and below the plane of the ring. The filled chloride orbital is equally likely to overlap with either lobe, leading to the chloride attaching either from above or below with equal likelihood.

- The two regioisomeric products of the reaction, major product and minor product (one of several stereoisomers), have an energy difference of 0.8 kcal/mol. The stereoisomers of the minor product and the stabilities of cyclic molecules will be explored in later sections.
Rationalizing this relative energy differences is beyond the scope of CHEM 343, but use this energy, along with information from part (c), to complete the reaction coordinate diagram below for the electrophilic addition of HCl to 1-methylcyclohexene. Label the locations of the transition states with a ‡ and the activation energy of the rate-determining step for each reaction pathway. A complete reaction coordinate diagram includes all reactants, products, and intermediates.Left-click here for a little more explanation.
Hammond’s postulate allows us to assume that the energy difference between the intermediates is roughly the same as the energy difference between the transition states (in other words, Ea,RDS, blue – Ea, RDS, pink ≈ 12 kcal/mol). - Making direct reference to the reaction coordinate diagram to rationalize the regiochemical outcome of this reaction. In other words, provide a theoretical explanation for Markovnikov’s rule. Include in your answer a discussion of the relevant energy difference and whether this reaction is under thermodynamic or kinetic control.
Write in your notebook, then left-click here.
The regiochemistry of this reaction is determined by the energy differences of the transition states to form the carbocations. Because the reaction is not reversible under the reaction conditions (reverse reaction barrier is very high), the rate of each reaction pathway determines that the Markovnikov product is favored from the tertiary carbocation. When the rate determines the outcome, the reaction is under kinetic control.
