3 Relative Energy of Alkene Isomers
The standard state enthalpy change for a reaction, ΔrH°, can be used to approximate the energy difference between reactants and products. It can be calculated using tabulated values of standard formation enthalpies, ΔfH°, by applying Hess’s law (which states that if a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps.):
ΔrH° = ∑ΔfH°(products) – ∑ΔfH°(reactants)
We can use ΔrH° to gauge the relative energy of reactant molecules vs. product molecules:
- A negative ΔrH° indicates the forward reaction is exothermic, where energy in the form of heat is released to the surroundings. In exothermic reactions, the total energy of the product molecules are lower than the total energy of the reactant molecules.
- For example, the reaction
C(s, graphite) + O2(g) ⟶ CO2(g) ΔrH° = −394 kJ/mol
is exothermic. In other words, 1 mole of CO2 is lower in energy than 1 mole of graphite and 1 mole of O2 combined.
- For example, the reaction
- A positive ΔrH° indicates the forward reaction is endothermic, where energy in the form of heat is absorbed from the surroundings. In endothermic reactions, the total energy of the product molecules are higher than the total energy of the reactant molecules.
- For example, the reaction
N2(g) + 2 O2(g) ⟶ 2 NO2(g) ΔrH° = +66 kJ/mol
is endothermic. In other words, 2 moles of NO2 is higher in energy than 1 mole of N2 and 2 moles of O2 combined.
- For example, the reaction
[Note: the above content likely will already exist in some form from previous chapter, especially when discussing acid/base strenghs. Will need to edit and incorporate better once those are written.]
When considering relative energies of alkene isomers, we can simply compare their ΔfH° because their enthalpy of formation reactions involve the same reactants. For example, the enthalpy of formation reaction for cis-2-butene is:
4 C(s, graphite) + 4 H2(g) ⟶ C4H8(g, cis-2-butene) ΔfH° = −7.1 kJ/mol
And the enthalpy of formation reaction for trans-2-butene is:
4 C(s, graphite) + 4 H2(g) ⟶ C4H8(g, trans-2-butene) ΔfH° = −11.4 kJ/mol
Therefore, trans-2-butene is lower in energy than cis-2-butene, by 4 kJ/mol.
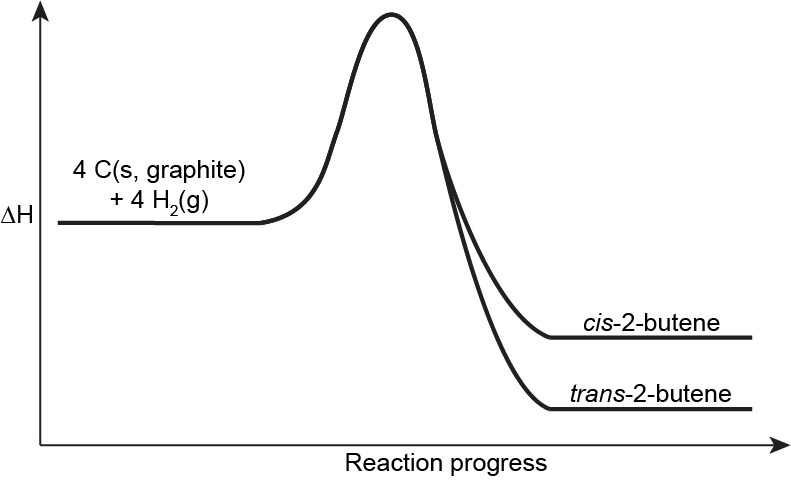
In general, the cis isomer of an alkene is higher in energy compared to the trans isomer. This is because the two alky groups being on the same side of the double bond leads to higher electron-electron repulsion, creating a steric strain [link to earlier content, alkane conformers] that distorts bond angles, leading to less effective bond orbital overlap and desabilizing the molecule. This steric strain is directly related to the size of the substituents on the alkene. For example, while the difference in energy between cis and trans methyl groups is ~5 kJ/mol (as in the case of 2-butene), the difference between cis and trans tert-butyl groups can be over 40 kJ/mol.
[should geminal disubstituted alkene be discussed? It is not as straightforward. ex: ΔfH° of isobutene is -17 kJ/mol, lowest of all butene isomers.]
In addition to the position of the alkyl groups, the number of substituents also influence alkene isomers’ relative energies. In general, tetrasubsituted alkenes are lower in energy than trisubstituted alkenes, which are lower in energy than disubstituted alkenes, which are lower in energy than monosubsituted alkenes.
This general trend is due to a combination of two factors: hyperconjugation and bond energies.
Hyperconjugation [link to first presentation of hyperconjugation] leads to electron delocalization via the overlap of the empty C-C π* orbital with adjacent filled C-H or C-C σ bonding orbitals. Without any substituents, i.e. in the case of C2H4, all the σ bonding orbitals are perpendicular to the π* orbital, and no hyperconjugation would be possible. However, with presence of alkyl substituents, for example, the methyl group in propene, hyperconjugation would lead to slight energy lowering of the filled σ bonding orbital in the subsituent.
And, as the number of alkyl substituents increases, the number of σ bonding orbital available for hyperconjugation increases, and the alkene tends to become lower in energy overall.
Bond strengths also play a part in determining the overall stability of a molecule. Due to the energy difference between a sp2 carbon and a sp3 carbon,[link to earlier chapter content] a C-C σ bond between a sp3 carbon and a sp2 carbon is slightly stronger (lower in energy) than a C-C σ bond between two sp3 carbons. An alkene with more alkyl substituents would have more σC(sp3)-C(sp2) bonds and less σC(sp3)-C(sp3) bonds, making it lower in energy compared to an isomer with less substituents.
Both hyperconjugation and bond strength play a part in relative energies of alkene isomers, such that, for example, 1-butene is 7 kJ/mol higher in energy than cis-2-butene.
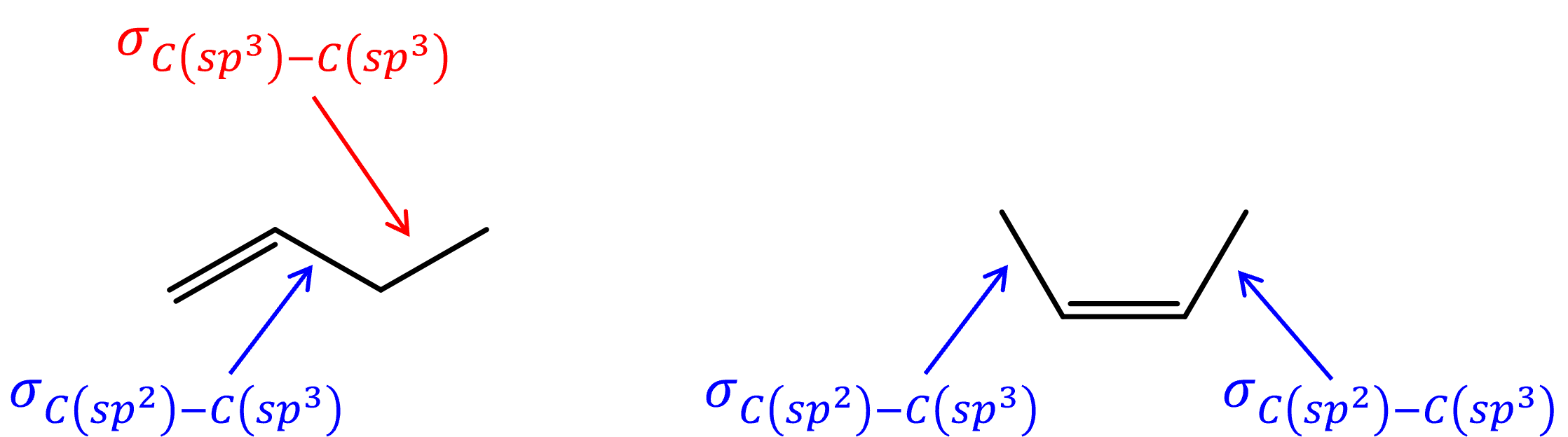
Exercise 1: Relative Energies of Isomers
Rank the following C6H12 alkene isomers from the highest expected heat of formation (ΔfH°) (first in sequence) to lowest ΔfH° (last in sequence).
