41 Core and Valence Electrons, Shielding, Zeff (M7Q8)

Introduction

This section continues to explore the relationship between an atom’s electron arrangement in orbitals and the chemical properties of that atom. As we move from hydrogen to multi-electron atoms there is an incredible increase in complexity due to the fact that electrons repel each other.  Nonetheless, one can still understand much of the periodic table and the trends in properties of atoms and ions by using approximations that are based on using the quantum numbers of individual electrons in an atom. These properties vary periodically as the electronic structure of the elements changes. They are (1) size (radius) of atoms and ions, (2) ionization energies, and (3) electron affinities. This section will focus on the properties governing the size (radius) of atoms and ions.

Learning Objectives for Core and Valence Electrons, Shielding, Zeff

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Effective Nuclear Charge (Zeff)

For an atom or an ion with only a single electron, we can calculate the potential energy of an electron by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. For example, in helium there are two electrons. From Coloumb’s law we know that there is a repulsive interaction that depends on the distance between them. In addition there are attractive interactions between each of the two electrons with the nucleus.  There are no known solutions to the Schrodinger equation for this problem, so one must use approximate methods to find the orbitals and their energies.

If an electron is far from the nucleus (i.e., if the distance r between the nucleus and the electron is large), then at any given moment, most of the other electrons will be between that electron and the nucleus. Hence these electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between the nucleus and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (Zeff). An effective nuclear charge is the nuclear charge an electron actually experiences because of shielding from other electrons closer to the nucleus (Figure 1). Consequently, the Zeff is always less than the actual nuclear charge, Z. The Zeff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present.

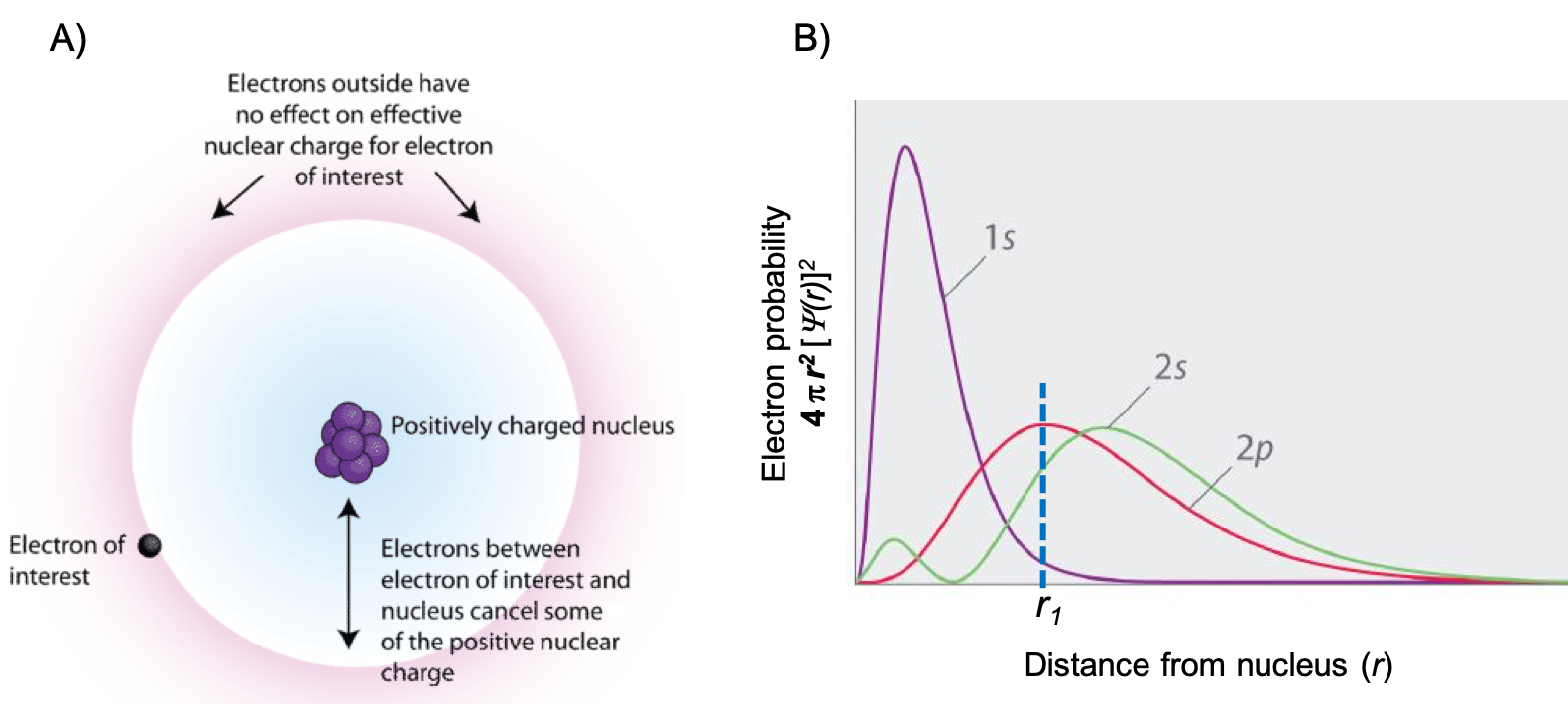
This figure has two parts: the left part is labeled “A” and the right part is labeled “B”. For part A, there is a representation of an atom. There is a blob of purple spheres in the center that is labeled “positively charged nucleus”. This is surrounded by a blue cloud. On the outside of the blue cloud is a red cloud. At the interface of the blue and red clouds is an electron labeled “electron of interest”. There is a double headed arrow in the blue cloud that points between the nucleus and the interface between the blue and red cloud that is labeled “electrons between electron of interest and nucleus cancel some of the positive nuclear charge”. There is an arrow pointing to the red cloud that states “Electrons outside have no effect on effective nuclear charge for electron of interest. In part B, there is a plot of electron probability versus distance from the nucleus (r). Electron probability is defined as 4 multiplied by pi multiplied by the radius squared multiplied by the wave function as a function of r squared. There are 3 curves plotted. A purple curve has one tall peak and is labeled “1 s”. A green trace has a small peak at about the same x value as the purple peak, but much smaller. Then it has a taller peak at a larger x value. Between the two peaks, the intensity dips back to zero. This curve is labeled “2 s”. The third trace is red and has a single peak at an x distance between the peak for the purple graph and the taller peak for the green graph. This trace is labeled “2 p”. A dotted line is drawn upward from x equals r subscript 1 on the x axis to the peak of the red curve.
Figure 1. The shielding effect. (A) The interior electron cloud (light blue) shields the outer electron of interest from the full attractive force of the nucleus. Electrons further from the nucleus (red) do not affect the Zeff between the electron of interest and the nucleus. (B) A plot of electron probability vs. distance from the nucleus shows that electrons in the 1s orbital are more likely to be found closer to the nucleus than electrons in the 2s or 2p orbitals. Only electrons that are likely to be found between the electron of interest and the nucleus contribute to shielding.
Shielding is determined by the probability of another electron being between the electron of interest and the nucleus, as well as by the electron–electron repulsions the electron of interest encounters. Core electrons are adept at shielding, while electrons in the same valence shell do not block the nuclear attraction experienced by each other as efficiently. In Figure 1B, if a 2p electron exists at a distance r1, most likely the 1s electrons (core electrons) will be between the electron of interest and the nucleus. But, there is only a small probability of the 2s electron (electron in the same valence shell) to shield the 2p electron of interest. Thus, each time we move from one element to the next across a period, Z increases by one, but the shielding increases only slightly. Thus, Zeff for valence electrons increases as we move from left to right across a period. In this class, we will calculate Zeff = Z – S, where S is the number of core electrons that are shielding the valence electrons. There are more exact ways of determining Zeff which include the shielding contribution of electrons in the same shell, but the approximate formula we use in this course is accurate enough to be very useful. Remember from a previous chapter, Z is the number of protons in the nucleus.

Note that while we often refer to the Zeff of a valence electron, we can calculate the Zeff for any electron by taking into account only the number of core electrons that are shielding. For example, consider a 2s electron of Cl. For Cl, Z = 17 and the electron configuration is 1s22s22p63s23p5. The only electrons that will shield a 2s electron are the 1s electrons, and there are two of them. Therefore, Zeff = 17 – 2 = 15 for a 2s electron of Cl. The Zeff for a 3p electron, on the other hand, is Zeff = 17 – 10 = 7 because there are 10 electrons shielding the 3p electron (2 electrons in n = 1 and a total of 8 electrons in n = 2).

Variation in Atomic Radius

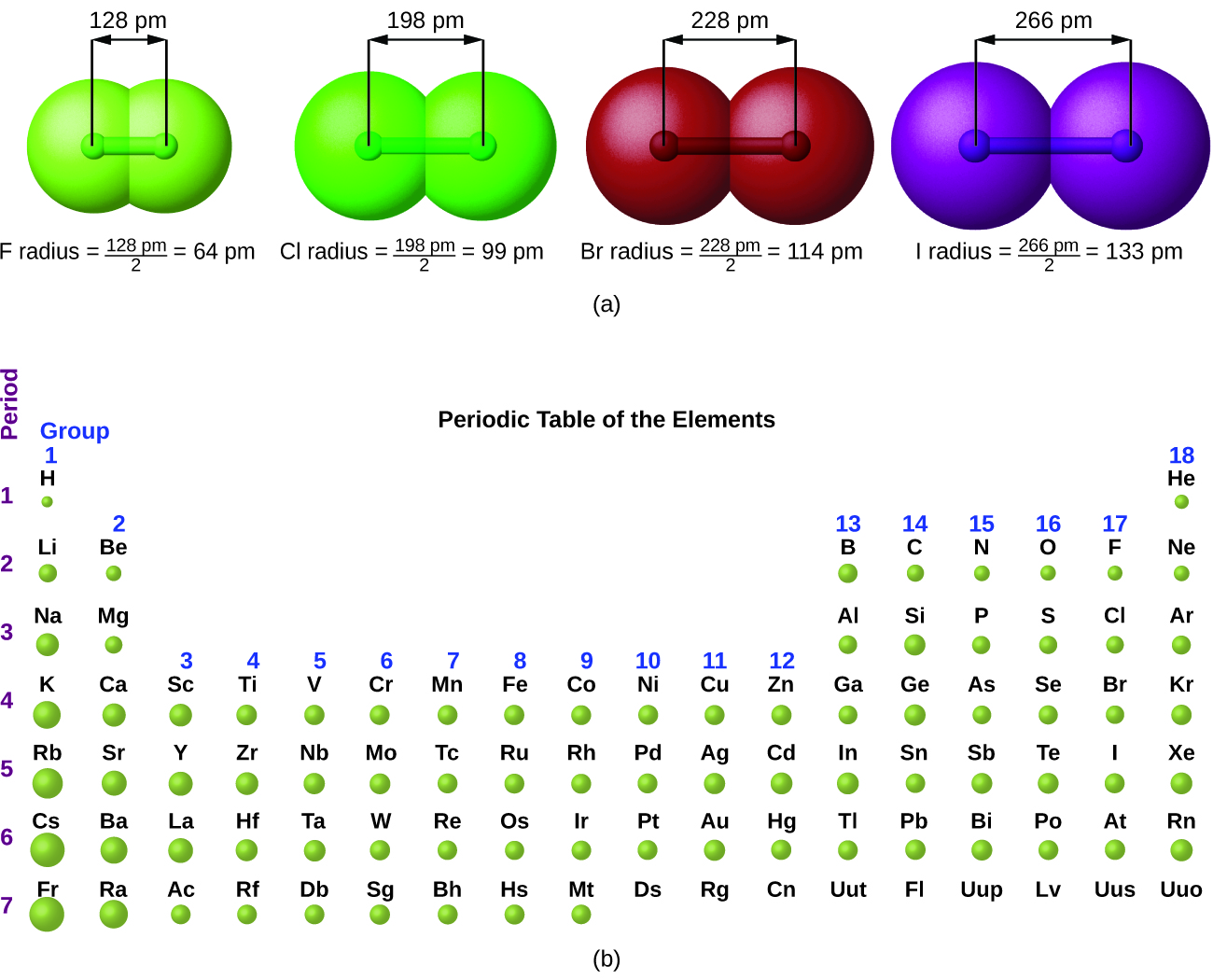
The quantum mechanical picture makes it difficult to establish a definite size of an atom. However, there are several practical ways to define the radius of atoms and, thus, to determine their relative sizes that give roughly similar values. We will use the atomic radii (Figure 2), which is defined as one-half the distance between the nuclei of two identical atoms when they are joined by a covalent bond (this measurement is possible because atoms within molecules still retain much of their atomic identity). We know that as we scan down a group, the principal quantum number, n, increases by one for each element. Thus, the electrons are being added to a region of space that is increasingly distant from the nucleus. Consequently, the size of the atom (and its atomic radius) must increase as we increase the distance of the outermost electrons from the nucleus. This trend is illustrated for the atomic radii of the halogens in Table 1 and Figure 2. The trends for the entire periodic table can be seen in Figure 2.

Atom Atomic radius (pm) Nuclear charge
F 64 +9
Cl 99 +17
Br 114 +35
I 133 +53
At 148 +85
Table 1. Covalent Radii of the Halogen Group Elements
This figure has two parts: a and b. In figure a, 4 diatomic molecules are shown to illustrate the method of determining the atomic radius of an atom. The first model, in light green, is used to find the F atom radius. Two spheres are pushed very tightly together. The distance between the centers of the two atoms is indicated above the diagram with a double headed arrow labeled, “128 p m.” The endpoints of this arrow connect to line segments that extend to the atomic radii below. Beneath the molecule is the label, “F radius equals 128 p m divided by 2 equals 64 p m.” The next three models are similarly used to show the atomic radii of additional atoms. The second diatomic molecule is in a darker shade of green. The distance between the radii is 198 p m. Beneath the molecule is the label, “C l radius equals 198 p m divided by 2 equals 99 pm.” The third diatomic molecule is in red. The distance between the radii is 228 p m. Beneath the molecule is the label, “B r radius equals 228 p m divided by 2 equals 114 pm.” The fourth diatomic molecule is in purple. The distance between the radii is 266 p m. Beneath the molecule is the label, “I radius equals 266 p m divided by 2 equals 133 p m.” In figure b, a periodic table layout is used to compare relative sizes of atoms using green spheres. No spheres are provided for the noble or inert gas, group 18 elements. General trends noted are increasing circle size moving from top to bottom in a group, with a general tendency toward increasing atomic radii toward the lower left corner of the periodic table.
Figure 2. (a) The radius of an atom is defined as one-half the distance between the nuclei in a molecule consisting of two identical atoms joined by a covalent bond. The atomic radius for the halogens increases down the group as n increases. (b) Covalent radii of the elements are shown to scale. The general trend is that radii increase down a group and decrease across a period.

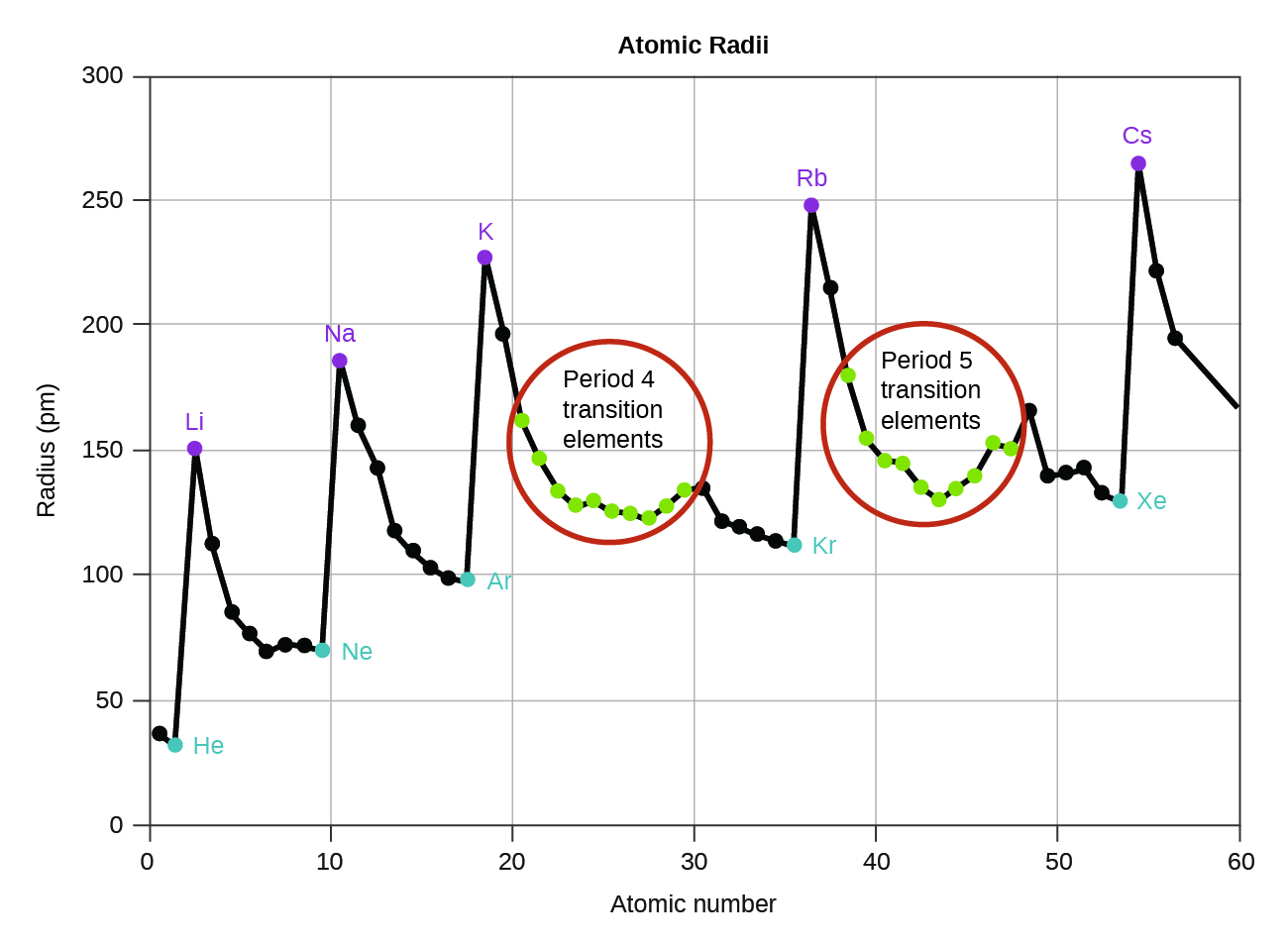
As shown in Figure 2, as we move across a period from left to right, we generally find that each element has a smaller atomic radius than the element preceding it. This is expected due to the Zeff for the valence electron increasing from left to right across a period, as we saw above. The stronger pull (higher effective nuclear charge) experienced by valence electrons on the right side of the periodic table draws them closer to the nucleus, making the atomic radii smaller.

This graph entitled, “Atomic Radii,” is labeled, “Atomic Number,” on the horizontal axis and, “Radius (p m),” on the vertical axis. Markings are provided every 10 units up to 60 on the horizontal axis beginning at zero. Vertical lines extend from the horizontal axis upward at each of these markings. The vertical axis begins at 0 and increases by 50’s up to 300. Horizontal lines are drawn across the graph at multiples of 50. A black jagged line connects the radii values for elements with atomic numbers 1 through 60 on the graph. Peaks are evident at the locations of the alkali metals: L i, N a, K, R b, and C s, at which points on the graph purple dots are placed and elements are labeled in purple. Similarly, minima exist at the locations of noble or inert gases: H e, N e, A r, K r, X e, and R n, at which points blue dots are placed and element symbols are provided in blue. The locations of period 4 and period 5 transition elements are provided with green dots. These points are clustered together in two locations on the graph which are circled in red and labeled accordingly. The green dots for the transition elements along with the line that connects them form a U shape on the graph within each of the red circles drawn. The atomic radii for the alkali metals in picometers are: L i 167, N a 190, K 243, R b 265, and C s 298. The atomic radii of the noble or inert gases included in the graph in picometers are: H e 31, N e 38, A r 71, K r 88, and X e 108.
Figure 3. Within each period, the trend in atomic radius decreases as Z increases; for example, from K to Kr. Within each group (e.g., the alkali metals shown in purple), the trend is that atomic radius increases as the n level (orbital size) increases.

 

Explore visualizations of the periodic trends discussed in this section (and many more trends). With just a few clicks, you can create three-dimensional versions of the periodic table showing atomic size or graphs of ionization energies from all measured elements.

 

Example 1

Sorting Atomic Radii
Predict the order of increasing atomic radius for Ge, Fl, Br, Kr.

Solution
Radius increases as we move down a group, so Ge < Fl (Note: Fl is the symbol for flerovium, element 114, NOT fluorine). Radius decreases as we move across a period, so Kr < Br < Ge. Putting the trends together, we obtain Kr < Br < Ge < Fl.

Check Your Learning
Give an example of an atom whose size is smaller than fluorine.

Answer:

Ne or He

Key Concepts and Summary

Effective nuclear charge for valence electrons increases from left to right across a period and decreases down a group. Because valence electrons are held more tightly on the right side of the Periodic Table, the atomic radius decreases. Atomic radius increases as we move down a group because the n level (orbital size) increases.

Key Equations

  • Zeff = Z – S, where S is the number of core electrons

Glossary

atomic radius
one-half the distance between the nuclei of two identical atoms when they are joined by a covalent bond
core electrons
electrons occupying the inner shell orbitals
effective nuclear charge
charge that leads to the Coulomb force exerted by the nucleus on an electron, calculated as the nuclear charge minus shielding

valence electrons
electrons in the outermost or valence shell (highest value of n) of a ground-state atom; determine how an element reacts

Chemistry End of Section Exercises

  1. Based on their positions in the periodic table, predict which has the smallest atomic radius: Mg, Sr, Si, Cl, I.
  2. Based on their positions in the periodic table, predict which has the largest atomic radius: Li, Rb, N, F, I.
  3. Atoms of which group in the periodic table have a valence shell electron configuration of ns2np3?
  4. Atoms of which group in the periodic table have a valence shell electron configuration of ns2?
  5. Based on their positions in the periodic table, list the following atoms in order of increasing radius: Mg, Ca, Rb, Cs.
  6. Based on their positions in the periodic table, list the following atoms in order of increasing radius: Sr, Ca, Si, Cl.

Answers to Chemistry End of Section Exercises

  1. Cl
  2. Rb
  3. 15 (5A)
  4. 2 (2A)
  5. Mg < Ca < Rb < Cs
  6. Cl < Si < Ca < Sr

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

UW-Madison Chemistry 103/104 Resource Book Copyright © by crlandis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book