16 Limiting Reagents (M4Q3)
Introduction
Learning Objectives for Limiting Reagents
- Identify limiting reagents; calculate theoretical and percent yields of products and quantities of excess reagents.
| Limiting Reactants | Percent Yield |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
The relative amounts of reactants and products represented in a balanced chemical equation are often referred to as stoichiometric amounts. All the exercises of the preceding section involved stoichiometric amounts of reactants. For example, when calculating the amount of product generated from a given amount of reactant, it was assumed that any other reactants required were available in stoichiometric amounts (or greater). In this module, more realistic situations are considered, in which reactants are not present in stoichiometric amounts.
Limiting Reactants
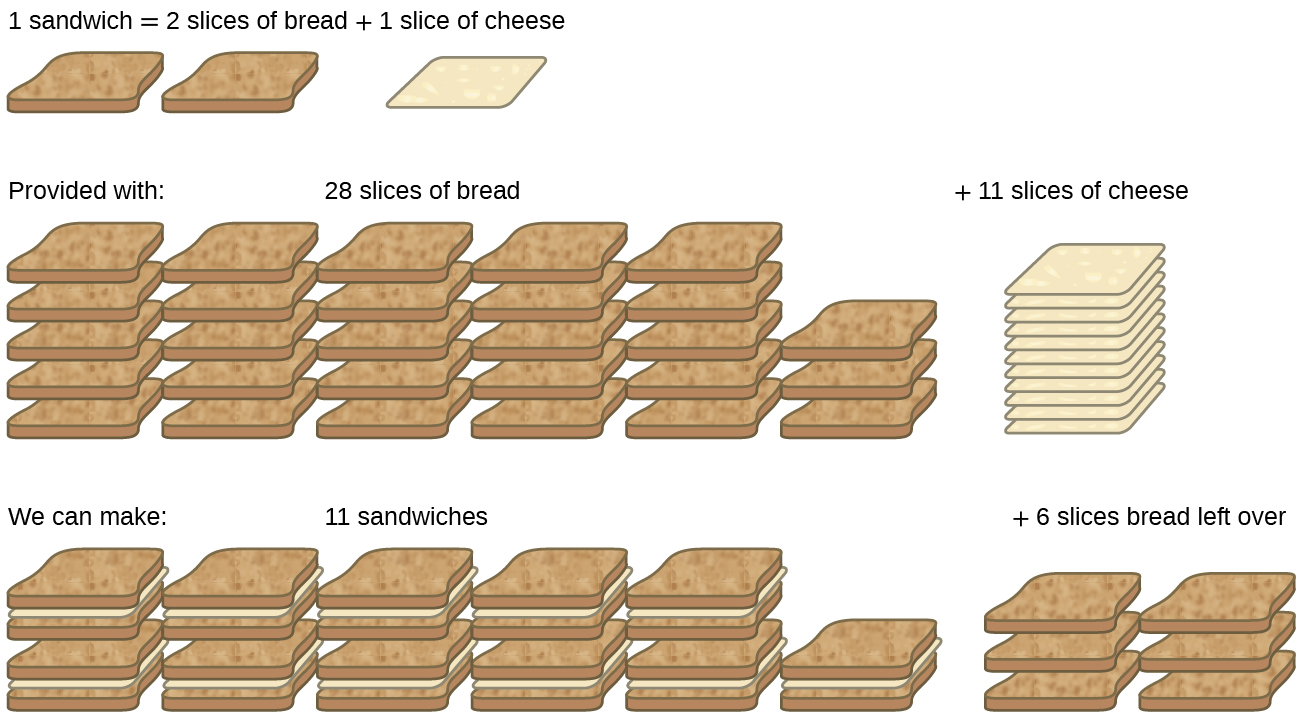
Consider another food analogy: making grilled cheese sandwiches (Figure 1):
1 slice of cheese + 2 slices of bread ⟶ 1 sandwich
Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio. Provided with 28 slices of bread and 11 slices of cheese, one may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread left over. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and the bread slices have been provided in excess.
Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:
H2(g) + Cl2(g) ⟶ 2 HCl(g)
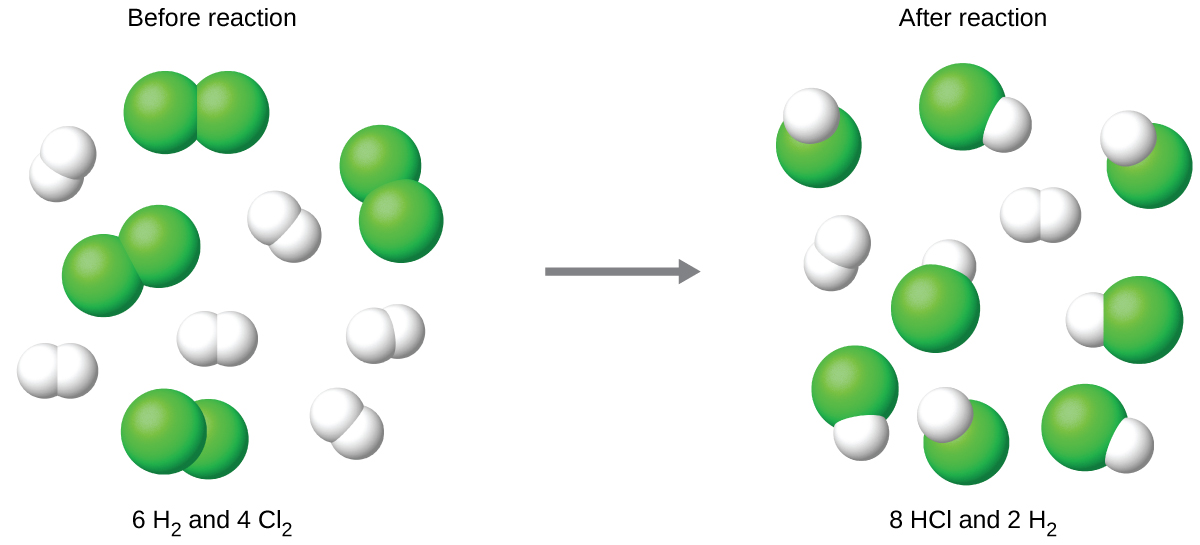
The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant/reagent, and the other substance is the excess reactant/reagent. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H2 and 2 moles of Cl2. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. Reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen unreacted.
An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant. For the example in the previous paragraph, complete reaction of the hydrogen would yield
mol HCl produced = 3 mol H2 × [latex]\frac{2\;\text{mol HCl}}{1\;\text{mol H}_2}[/latex] = 6 mol HCl
Complete reaction of the provided chlorine would produce
mol HCl produced = 2 mol Cl2 × [latex]\frac{2\;\text{mol HCl}}{1\;\text{mol Cl}_2}[/latex] = 4 mol HCl
The chlorine will be completely consumed once 4 moles of HCl have been produced. Since enough hydrogen was provided to yield 6 moles of HCl, there will be unreacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure 2).

View this interactive simulation illustrating the concepts of limiting and excess reactants.
Demonstration: Limiting reactants are completely consumed in the reaction
Set up. The following video demonstrates that a limiting reactant (or limiting reagent) is completely consumed during a reaction. There are two containers, each with about 0.61 g of solid magnesium in water (the water is not reacting at all). To the left container, 50 mL of 6.0 M HCl(aq) is added, and to the right container, 50 mL or 1.0 M HCl(aq) is added.
Prediction. Before watching the video, write the reaction equation and make a prediction about which reactant will be limiting in each case.
Explanation. The reaction occurring in this demonstration is:
Mg(s) + 2 HCl(aq) → MgCl2(aq) + H2(g)
In the left container, with the higher concentration of HCl, the magnesium is the limiting reactant. At the end of the reaction, there is no more visible magnesium in the container. In the right container, with the lower concentration of HCl, the HCl is the limiting reactant. Even after 30 min, some magnesium remains in the container unreacted. This is because all the HCl has been consumed and there is no more HCl to complete the reaction. The limiting reactant is completely consumed in the reaction and the reaction then ceases.
Example 1
Identifying the Limiting Reactant
Silicon nitride is a very hard, high-temperature-resistant ceramic used as a component of turbine blades in jet engines. It is prepared according to the following equation:
Which is the limiting reactant when 2.00 g of Si and 1.50 g of N2 react?
What mass of Si3N4 is made and what mass of excess reagent remains after the reaction has gone to completion?
Solution
Compute the provided molar amounts of reactants, and then compare these amounts to the balanced equation to identify the limiting reactant.
The provided Si:N2 molar ratio is:
The stoichiometric Si:N2 ratio is:
Comparing these ratios shows that Si is provided in a less-than-stoichiometric amount, and so is the limiting reactant.
Alternatively, compute the amount of product expected for complete reaction of each of the provided reactants. The 0.0712 moles of silicon would yield
mol Si3N4 produced = 0.0712 mol Si × [latex]\frac{1 \;\text{mol Si}_3 \text{N}_4}{3 \;\text{mol Si}}[/latex] = 0.0237 mol Si3N4
while the 0.0535 moles of nitrogen would produce
Since silicon yields the lesser amount of product, it is the limiting reactant.
Now we know the limiting reagent produces 0.0237 mol of product, the mass of Si3N4 can be determined by utilizing the molar mass of Si3N4:
0.0237 mol Si3N4 × [latex]\frac{140.3 \;\text{g}}{1 \;\text{mol Si}_3 \text{N}_4}[/latex] = 3.33 g Si3N4
In order to determine the amount of N2 remaining, first, the amount of N2 must be determined:
0.0712 mol Si × [latex]\frac{2 \;\text{mol N}_2}{3 \;\text{mol Si}}[/latex] = 0.0475 mol N2
Subtracting this quantity from the amount of N2 provide will give what remains:
0.0535 mol N2 – 0.0475 mol N2 = 0.00604 mol N2
0.00604 mol N2 × [latex]\frac{28.01 \;\text{g}}{1 \;\text{mol N}_2}[/latex] = 0.169 g N2
Check Your Learning
Which is the limiting reactant when 5.00 g of H2 and 10.0 g of O2 react and form water?
How many grams of water are formed and what mass of excess reagent remains?
Answer:
O2; 11.3 g H2O produced; 3.74 g H2 remains in excess.
Percent Yield
The amount of product that may be produced by a reaction under specified conditions, as calculated per the stoichiometry of an appropriate balanced chemical equation, is called the theoretical yield of the reaction (previous calculations for how much product is produced using stoichiometry were also theoretical yields since they were the expected amount and were not found by doing an experiment in a lab). In practice, the amount of product obtained is called the actual yield, and it is often less than the theoretical yield for a number of reasons. Some reactions are inherently inefficient, being accompanied by side reactions that generate other products. Others are, by nature, incomplete (consider the partial reactions of weak acids and bases discussed in the previous module). Some products are difficult to collect without some loss, and so less than perfect recovery will reduce the actual yield. The extent to which a reaction’s theoretical yield is achieved is commonly expressed as its percent yield:
percent yield = [latex]\frac{\text{actual yield}}{\text{theoretical yield}}[/latex] × 100%
Actual and theoretical yields may be expressed as masses or molar amounts (or any other appropriate property; e.g., volume, if the product is a gas). As long as both yields are expressed using the same units, these units will cancel when percent yield is calculated.
Example 2
Calculation of Percent Yield
Upon reaction of 1.274 g of copper sulfate with excess zinc metal, 0.392 g copper metal was obtained according to the equation:
What is the percent yield?
Solution
The provided information identifies copper sulfate as the limiting reactant, and so the theoretical yield is found by the approach illustrated in the previous module, as shown here:
1.274 g CuSO4 × [latex]\frac{1 \;\rule[0.25ex]{4em}{0.1ex}\hspace{-4em}\text{mol CuSO}_4}{159.62 \;\rule[0.25ex]{3em}{0.1ex}\hspace{-3em}\text{g CuSO}_4}[/latex] × [latex]\frac{1 \;\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol Cu}}{1 \rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol CuSO}_4}[/latex] × [latex]\frac{63.55 \;\text{g Cu}}{1 \;\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol Cu}}[/latex] = 0.5072 g Cu
Using this theoretical yield and the provided value for actual yield, the percent yield is calculated to be
percent yield = [latex]\frac{0.392\;\text{g Cu}}{0.5072\;\text{g Cu}}[/latex] = 77.3%
Check Your Learning
What is the percent yield of a reaction that produces 12.5 g of the gas Freon CF2Cl2 from 32.9 g of CCl4 and excess HF?
Answer:
48.3%
Green Chemistry and Atom Economy
The purposeful design of chemical products and processes that minimize the use of environmentally hazardous substances and the generation of waste is known as green chemistry. Green chemistry is a philosophical approach that is being applied to many areas of science and technology, and its practice is summarized by guidelines known as the “Twelve Principles of Green Chemistry” (see details at this EPA website). One of the 12 principles is aimed specifically at maximizing the efficiency of processes for synthesizing chemical products. The atom economy of a process is a measure of this efficiency, defined as the percentage by mass of the final product of a synthesis relative to the masses of all the reactants used:
Though the definition of atom economy at first glance appears very similar to that for percent yield, be aware that this property represents a difference in the theoretical efficiencies of different chemical processes. The percent yield of a given chemical process, on the other hand, evaluates the efficiency of a process by comparing the yield of product actually obtained to the maximum yield predicted by stoichiometry.
The synthesis of the common nonprescription pain medication, ibuprofen, nicely illustrates the success of a green chemistry approach (Figure 3). First marketed in the early 1960s, ibuprofen was produced using a six-step synthesis that required 514 g of reactants to generate each mole (206 g) of ibuprofen, an atom economy of 40%. In the 1990s, an alternative process was developed by the BHC Company (now BASF Corporation) that requires only three steps and has an atom economy of ~80%, nearly twice that of the original process. The BHC process generates significantly less chemical waste; uses less-hazardous and recyclable materials; and provides significant cost-savings to the manufacturer (and, subsequently, the consumer). In recognition of the positive environmental impact of the BHC process, the company received the Environmental Protection Agency’s Greener Synthetic Pathways Award in 1997.
![This figure is labeled, “a,” and, “b.” Part a shows an open bottle of ibuprofen and a small pile of ibuprofen tablets beside it. Part b shows a reaction along with line structures. The first line structure looks like a diagonal line pointing down and to the right, then up and to the right and then down and to the right. At this point it connects to a hexagon with alternating double bonds. At the first trough there is a line that points straight down. From this structure, there is an arrow pointing downward. The arrow is labeled, “H F,” on the left and “( C H subscript 3 C O ) subscript 2 O,” on the right. The next line structure looks exactly like the first line structure, but it has a line angled down and to the right from the lower right point of the hexagon. This line is connected to another line which points straight down. Where these two lines meet, there is a double bond to an O atom. There is another arrow pointing downward, and it is labeled, “H subscript 2, Raney N i.” The next structure looks very similar to the second, previous structure, except in place of the double bonded O, there is a singly bonded O H group. There is a final reaction arrow pointing downward, and it is labeled, “C O, [ P d ].” The final structure is similar to the third, previous structure except in place of the O H group, there is another line that points down and to the right to an O H group. At these two lines, there is a double bonded O.](https://wisc.pb.unizin.org/app/uploads/sites/126/2017/08/CNX_Chem_04_04_GreenChem.jpg)
Key Concepts and Summary
When reactions are carried out using less-than-stoichiometric quantities of reactants, the amount of product generated will be determined by the limiting reactant. The amount of product actually generated by a chemical reaction is its actual yield (found by doing an experiment in the lab). This yield is often less than the amount of product predicted by the stoichiometry of the balanced chemical equation representing the reaction (its theoretical yield). The extent to which a reaction generates the theoretical amount of product is expressed as its percent yield.
Key Equations
- percent yield = [latex]\frac{\text{actual yield}}{\text{theoretical yield}}[/latex] × 100%
Glossary
- actual yield
- amount of product formed in a reaction
- excess reactant
- reactant present in an amount greater than required by the reaction stoichiometry
- limiting reactant
- reactant present in an amount lower than required by the reaction stoichiometry, thus limiting the amount of product generated
- percent yield
- measure of the efficiency of a reaction, expressed as a percentage of the theoretical yield
- theoretical yield
- amount of product that may be produced from a given amount of reactant(s) according to the reaction stoichiometry
Chemistry End of Section Exercises
- The following quantities are placed in a container: 1.5 × 1024 atoms of hydrogen, 1.0 mol of sulfur, and 88.0 g of diatomic oxygen.
- What is the total mass in grams for the collection of all three elements?
- What is the total number of atoms for the three elements?
- If the mixture of the three elements formed a compound with molecules that contain two hydrogen atoms, one sulfur atom, and four oxygen atoms, which substance is consumed first?
- How many atoms of each remaining element would remain unreacted in the change described in (c)?
- What is the limiting reactant in a reaction that produces sodium chloride from 8.0 g of sodium and 8.0 g of diatomic chlorine? What mass of product is formed and what mass of excess reagent remains?
- A sample of 0.53 g of carbon dioxide was obtained by heating 1.31 g of calcium carbonate. What is the percent yield for this reaction?
CaCO3(s) → CaO(s) + CO2(g)
- Freon-12, CCl2F2, has been banned and is no longer used as a refrigerant because it catalyzes the decomposition of ozone and has a very long lifetime in the atmosphere. It is prepared from CCl4 reacting with HF. The other product of this reaction is HCl. Outline the steps needed to determine the percent yield of a reaction that produces 12.5 g of CCl2F2 from 32.9 g of CCl4. Determine the percent yield.
- Citric acid, C6H8O7, a component of jams, jellies, and fruity soft drinks, is prepared industrially via fermentation of sucrose by the mold Aspergillus niger. The equation representing this reaction is
C12H22O11 + H2O + 3 O2 → 2 C6H8O7 + 4 H2O
What mass of citric acid is produced from exactly 1 metric ton (1.000 × 103 kg) of sucrose if the yield is 92.30%?
- In a laboratory experiment, the reaction of 3.0 mol of H2 with 2.0 mol of I2 produced 1.0 mol of HI. Determine the theoretical yield in grams and the percent yield for this reaction.
- Outline the steps needed to solve the following problem, then do the calculations. Ether, (C2H5)2O, which was originally used as an anesthetic but has been replaced by safer and more effective medications, is prepared by the reaction of ethanol with sulfuric acid.
2 C2H5OH + H2SO4 → (C2H5)2O + H2SO4·H2O
What is the percent yield of ether if 1.17 L (d = 0.7134 g/mL) is isolated from the reaction of 1.500 L of C2H5OH (d = 0.7894 g/mL)?
- Outline the steps needed to determine the limiting reactant when 30.0 g of propane, C3H8, is burned with 75.0 g of oxygen. Determine the limiting reactant.
- What is the limiting reactant when 1.50 g of lithium and 1.50 g of nitrogen combine to form lithium nitride, a component of advanced batteries, according to the following unbalanced equation?
Li + N2 → Li3N
- Uranium can be isolated from its ores by dissolving it as UO2(NO3)2, then separating it as solid UO2(C2O4)·3H2O. Addition of 0.4031 g of sodium oxalate, Na2C2O4, to a solution containing 1.481 g of uranyl nitrate, UO2(NO3)2, yields 1.073 g of solid UO2(C2O4)·3H2O.
Na2C2O4 + UO2(NO3)2 + 3 H2O → UO2(C2O4) · 3 H2O + 2 NaNO3
Determine the limiting reactant and the percent yield of this reaction.
- How many molecules of the sweetener saccharin can be prepared from 30 C atoms, 25 H atoms, 12 O atoms, 8 S atoms, and 14 N atoms?
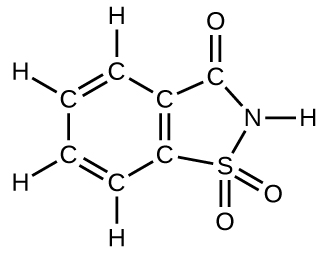
- The phosphorus pentoxide used to produce phosphoric acid for cola soft drinks is prepared by burning phosphorus in oxygen.
- What is the limiting reactant when 0.200 mol of P4 and 0.200 mol of O2 react according to
P4 + 5 O2 → P4O10
- Calculate the percent yield if 10.0 g of P4O10 is isolated from the reaction.
- What is the limiting reactant when 0.200 mol of P4 and 0.200 mol of O2 react according to
- Would you agree to buy 1 trillion (1,000,000,000,000) gold atoms for $5? Explain why or why not. Find the current price of gold at http://money.cnn.com/data/commodities/ (1 troy ounce = 31.1 g)
Answers to Chemistry End of Section Exercises
- (a) 122.6 g; (b) 5.4 × 1024 atoms; (c) Sulfur is the first consumed; (d) 3.0 × 1023 H atoms, 9.0 × 1023 O atoms
- The limiting reactant is Cl2. 13 g of NaCl is formed. 2.8 g of excess Na remains.
- percent yield = 92%
- g CCl4 ⟶ mol CCl4 ⟶ mol CCl2F2 ⟶ g CCl2F2, percent yield = 48.3%
- 1.036 × 103 kg or 1.036 × 106 g of citric acid
- theoretical yield = 511 g HI, percent yield = 25%
- Convert mass of ethanol to moles of ethanol; relate the moles of ethanol to the moles of ether produced using the stoichiometry of the balanced equation. Convert moles of ether to grams; divide the actual grams of ether (determined through the density) by the theoretical mass to determine the percent yield; percent yield = 87.6%
- Convert grams of propane to moles of carbon dioxide, then convert grams of oxygen to moles of carbon dioxide. Whichever results in the smaller amount of moles of carbon dioxide determines the limiting reagent. Oxygen is the limiting reagent.
- Lithium is the limiting reactant
- Na2C2O4 is the limiting reactant. percent yield = 86.6%
- Only four molecules can be made.
- (a) oxygen is the limiting reagent; (b) percent yield = 88.0%
- This amount cannot be weighted by ordinary balances and is worthless.

